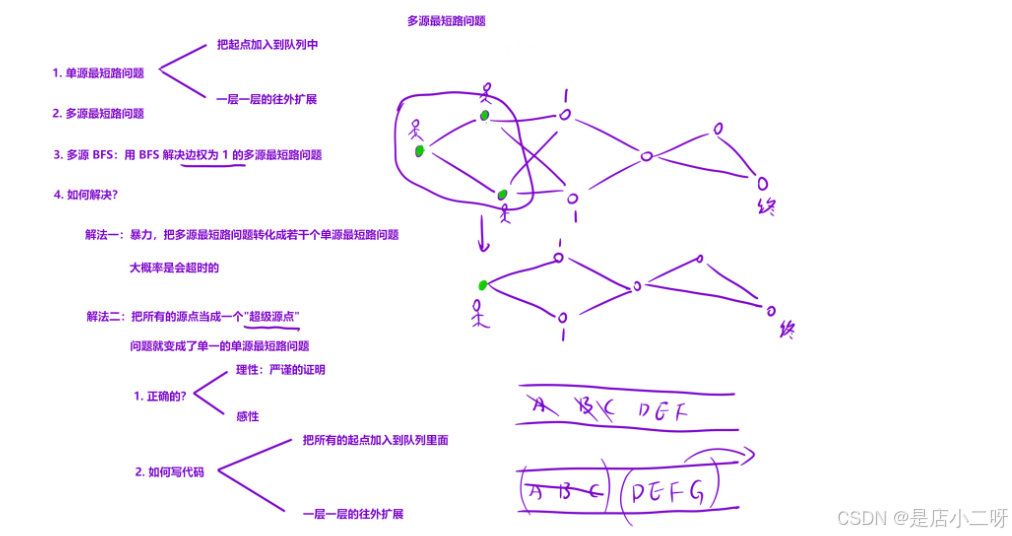
【优选算法-多源 BFS】多源 BFS:解决多个起点的广度优先搜索

| 算法 | 相关知识点 | 可以通过点击 | 以下链接进行学习 | 一起加油! |
|---|---|---|---|---|
| BFS 解决最短路问题 | BFS解决拓扑排序 |
多源广度优先搜索(BFS)是一种在图算法中非常实用的技术,它通过同时从多个源点开始搜索,能够高效地解决一些复杂问题,特别是在处理多个起点的最短路径或传播问题时。与传统的单源 BFS 相比,多源 BFS 可以显著减少计算量和提高搜索效率。本文将探讨多源 BFS 的基本原理、应用场景及其与普通 BFS 的区别,并展示如何利用多源 BFS 来优化图算法,解决实际问题。


🌈个人主页:是店小二呀
🌈C/C++专栏:C语言\ C++
🌈初/高阶数据结构专栏: 初阶数据结构\ 高阶数据结构
🌈Linux专栏: Linux
🌈算法专栏:算法
🌈Mysql专栏:Mysql
🌈你可知:无人扶我青云志 我自踏雪至山巅 
文章目录
- 542. 01 矩阵
- 1020. 飞地的数量
- 1765. 地图中的最高点
- 1162. 地图分析
本专题旨在解决 多源 BFS 问题,具体是利用 BFS 算法解决 边权为 1 的多源最短路径问题。
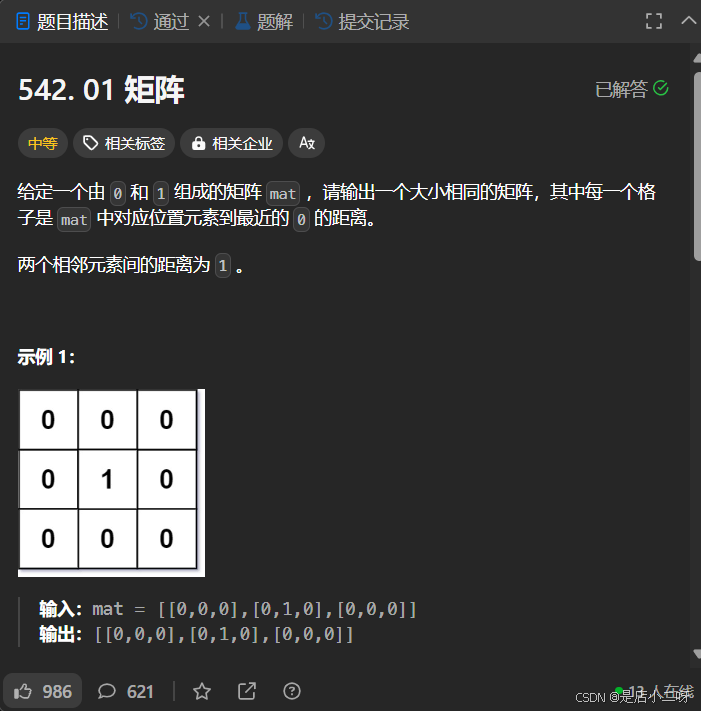
542. 01 矩阵
【题目】:542. 01 矩阵
【算法思路】
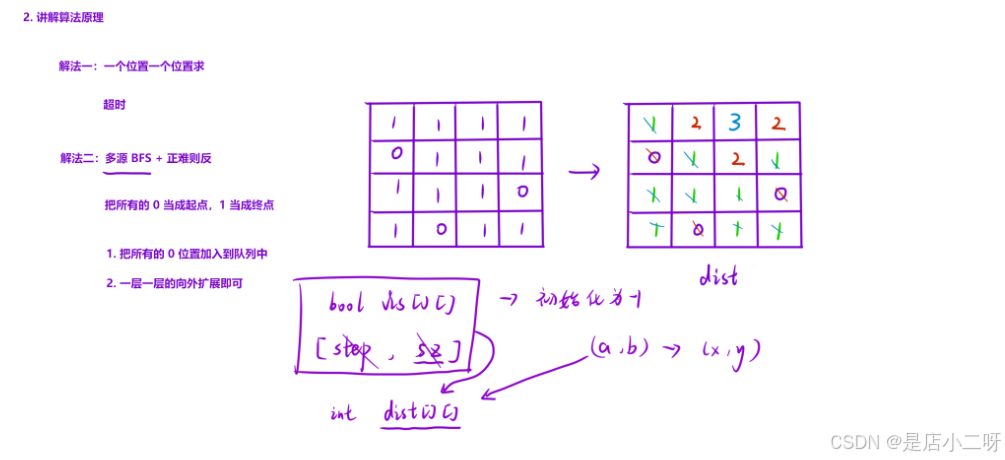
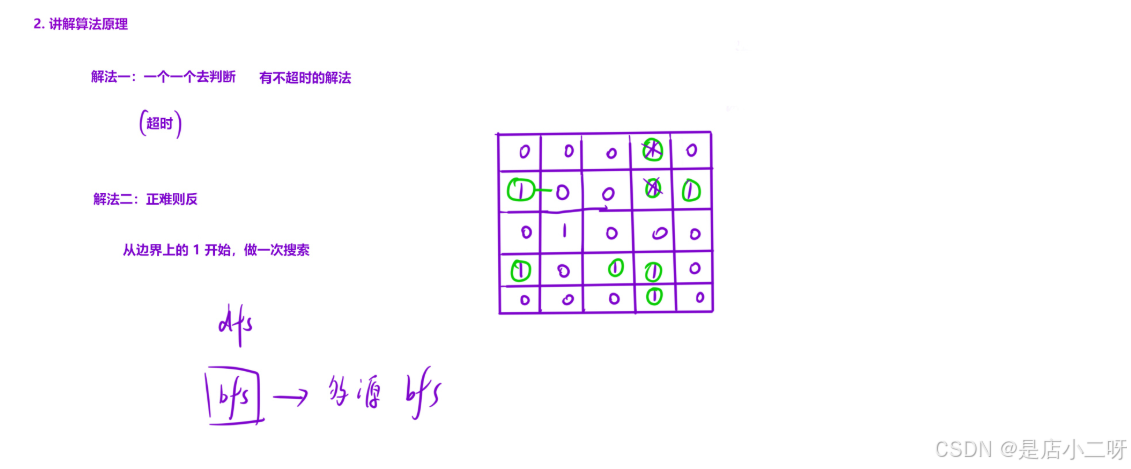
对于多源 BFS 问题,通常会为每个源点执行一次单源 BFS,但这种做法容易超时。我们可以采用 正难则反 的思路,将所有的 0 作为起点,1 作为终点,从而避免多次 BFS。
具体地,利用 超级起点 的思路,将所有的 0 的位置加入队列,开始一层层向外扩展。
在此过程中,为了避免重复遍历,我们不需要额外的 bool vis[][] 数组。通过将 dist[][] 初始化为 -1 来表示未访问过的节点,当一个节点被访问时,我们用 dist[x][y] = dist[a][b] + 1 来记录它的最短路径长度,相当于同时完成了遍历和层序遍历的功能。
【代码实现】
class Solution {
public:int dx[4] = {1, -1, 0, 0};int dy[4] = {0, 0, 1, -1};vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {int m = mat.size(), n = mat[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));queue<pair<int, int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(mat[i][j] == 0) {q.push({i, j}); dist[i][j] = 0;}while(!q.empty()){auto [a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){dist[x][y] = dist[a][b] + 1;q.push({x, y});}}}return dist;}
};
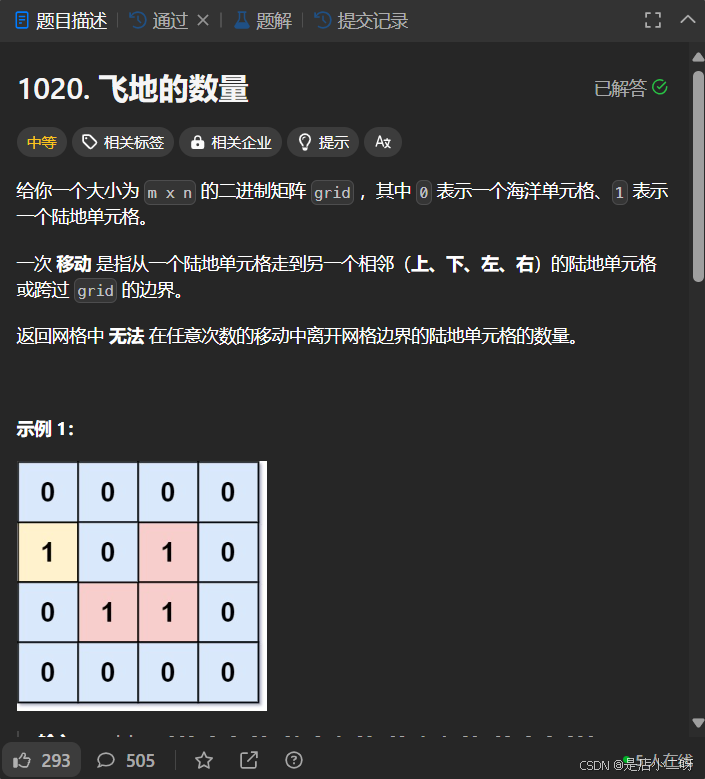
1020. 飞地的数量
【题目】:1020. 飞地的数量
【算法思路】
这道题和‘130. 被围绕的区域’很相似,但不同的是,这里不需要修改原矩阵元素。我们可以借鉴‘130’的解法,首先处理边界元素,然后遍历矩阵,统计未被标记的区域数量。
这道题我们可以先处理边界情况,对边界上的1进行BFS,并标记为true。然后遍历矩阵,基于vis矩阵统计符合条件的数量。这两种解法都可以实现
原来[sz, step]是一起使用的,本道题while(sz--)其实是多余的,可以去掉。
【代码实现】
class Solution {
public:int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};bool vis[501][501];int m, n;int numEnclaves(vector<vector<int>>& grid) {m = grid.size(), n = grid[0].size();queue<pair<int, int>> q;//1.处理边界情况,设置为truefor(int i = 0; i < m; i++){if(grid[i][0] == 1){q.push({i, 0});vis[i][0] = true;}if(grid[i][n - 1] == 1){q.push({i, n - 1});vis[i][n - 1] = true;}}for(int j = 0; j < n; j++){if(grid[0][j] == 1){q.push({0, j});vis[0][j] = true;}if(grid[m - 1][j] == 1){q.push({m - 1, j});vis[m - 1][j] = true;}}//2.进行BFSwhile(!q.empty()){auto[a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && !vis[x][y]){q.push({x, y});vis[x][y] = true;}}}//3.遍历数组int ret = 0;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j] == 1 && !vis[i][j])ret++;return ret;}
};1765. 地图中的最高点
【题目】:1765. 地图中的最高点
【算法思路】

如果直接求‘陆地到海洋的最大距离’比较困难,可以将问题转化为求‘海洋到陆地的最大距离’,因为两者的距离是对称的。通过利用‘连通块’和‘BFS’遍历,可以在题目要求的遍历次数内求解,简化了问题。
【代码实现】
class Solution {
public:int m, n;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {m = isWater.size(), n = isWater[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));//1.找到起始位置queue<pair<int, int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(isWater[i][j]){q.push({i, j});dist[i][j] = 0;}while(!q.empty()){auto[a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){q.push({x, y});dist[x][y] = dist[a][b] + 1;}}}return dist;}
};
1162. 地图分析
【题目】:1162. 地图分析
【算法思路】
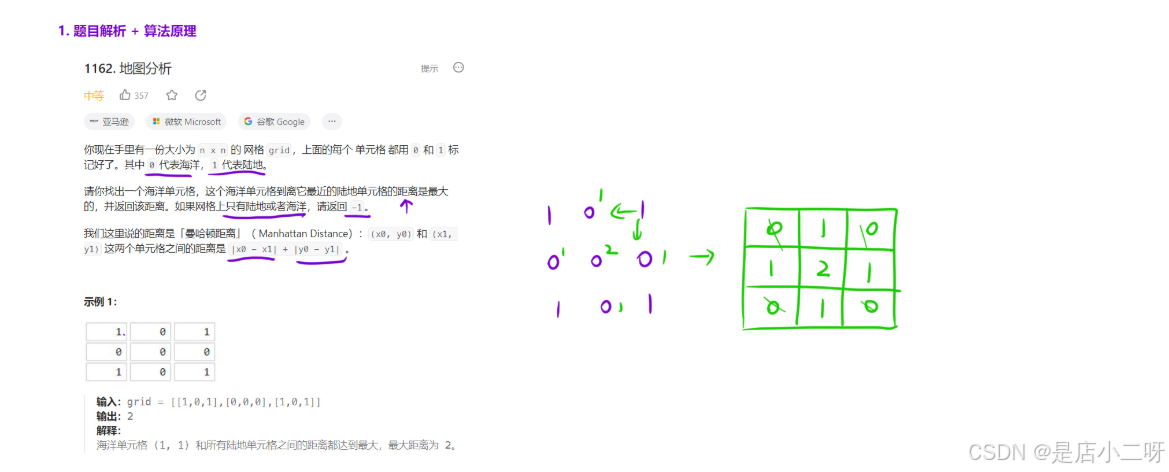
算法思路与‘1765. 地图中的最高点’类似,代码也大致相同。如果直接求‘海洋到陆地的最大距离’比较困难,可以将问题转化为求‘陆地到海洋的最大距离’,因为两者的距离是对称的。通过利用‘连通块’和‘BFS’遍历,可以在题目要求的遍历次数内求解,简化了问题。
【代码实现】
class Solution {
public:int m, n;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};int maxDistance(vector<vector<int>>& grid){m = grid.size(), n = grid[0].size();vector<vector<int>> dist(m, vector<int>(n, -1));//1.找到起始位置queue<pair<int, int>> q;for(int i = 0; i < m; i++)for(int j = 0; j < n; j++)if(grid[i][j]){q.push({i, j});dist[i][j] = 0;}int ret = -1;while(!q.empty()){auto[a, b] = q.front();q.pop();for(int k = 0; k < 4; k++){int x = a + dx[k], y = b + dy[k];if(x >= 0 && x < m && y >= 0 && y < n && dist[x][y] == -1){q.push({x, y});dist[x][y] = dist[a][b] + 1;ret = max(ret, dist[x][y]);}}}return ret;}
};
