当前位置：首页 > news >正文

TGD第二篇：破局——去除导数计算中的无穷小极限

news 2025/7/27 6:09:42

1. 用“积分”算“微分”：从传统导数到Lanczos导数

传统导数被定义为该极限形式：

$f′(x)=lim⁡Δx→0f(x+Δx)−f(x)Δxf^{\prime}\left(x\right)=\lim_{\Delta x \rightarrow 0} \frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}$

如果是可导点，左右导数存在且相等，则：

$f′(x)=lim⁡Δx→0f(x+Δx)−f(x)Δx=lim⁡Δx→0f(x)−f(x−Δx)Δx=lim⁡Δx→0f(x+Δx)−f(x−Δx)2Δxf^{\prime}\left(x\right)=\lim_{\Delta x \rightarrow 0} \frac{f\left(x+\Delta x\right)-f\left(x\right)}{\Delta x}=\lim_{\Delta x \rightarrow 0} \frac{f\left(x\right)-f\left(x-\Delta x\right)}{\Delta x}=\lim_{\Delta x \rightarrow 0} \frac{f\left(x+\Delta x\right)-f\left(x-\Delta x\right)}{2\Delta x}$

用一句通俗的话来理解，对于连续光滑函数而言，传统的导数刻画函数在该点的变化率，计算方式为 “右减左” 。

注意看，这里的”右“，是右边（无限临近求导点）的一个点函数值 $f(x+Δx)f\left(x+\Delta x\right)$ ；”左“，是左边（无限临近求导点）的一个点函数值 $f(x−Δx)f\left(x-\Delta x\right)$ ，分母是两个点之间的距离 $2Δx2\Delta x$ 。

此时，我再换个写法（实则加了几个数字“1”而已），将会带来全新的解读：

$f′(x)=lim⁡Δx→0f(x+Δx)−f(x−Δx)2Δx=lim⁡Δx→01⋅f(x+Δx)−1⋅f(x−Δx)(1⋅Δx)+(1⋅Δx)f^{\prime}\left(x\right)=\lim_{\Delta x \rightarrow 0} \frac{f\left(x+\Delta x\right)-f\left(x-\Delta x\right)}{2\Delta x}=\lim_{\Delta x \rightarrow 0} \frac{1·f\left(x+\Delta x\right)-1·f\left(x-\Delta x\right)}{(1·\Delta x)+(1·\Delta x)}$

加入了几个 $1$ 之后，这个公式有了新的解读，首先 $Δx\Delta x$ 可以被视作一个区间的长度， $1$ 是注意力关注度的总能量（假设总关注度是 100%），为了更方便理解，我加入了一个“·”作为乘号。即，为了求解导数，关注了 $\Delta x, x+\Delta x]$ 整个区间中的值，其中 $Δx\Delta x$ 无限趋近于0，区间无限窄。

此时，分子中的 $1⋅f(x+Δx)1·f\left(x+\Delta x\right)$ 意味着在求导点右侧区间 $x+\Delta x]$ 中只关注了距离最远的区间端点，分子中的 $1⋅f(x−Δx)1·f\left(x-\Delta x\right)$ 意味着求导点左侧区间 $[x−Δx,x)[x-\Delta x,x)$ 中只关注了距离最远的区间端点，导数计算依旧为 “右减左” ，即仅用最右侧区间端点函数值减去最左侧区间端点函数值，尽管 这个区间无穷小 罢了。

分母我将 $2Δx2\Delta x$ 写成了 $(1⋅Δx)+(1⋅Δx)(1·\Delta x) + (1·\Delta x)$ ，请注意，这 不是将两个区间的长度进行相加，而是算的两个区间的重心之间的距离 。重心，也就是观测区间在注意力加持下等效浓缩出来的点，分母是重心之间的距离，相当make sense。因为此时我的关注度100%全集中在区间的两侧端点，所以重心也恰好就在区间的两侧端点，重心之间的距离刚好是两个区间长度和罢了。

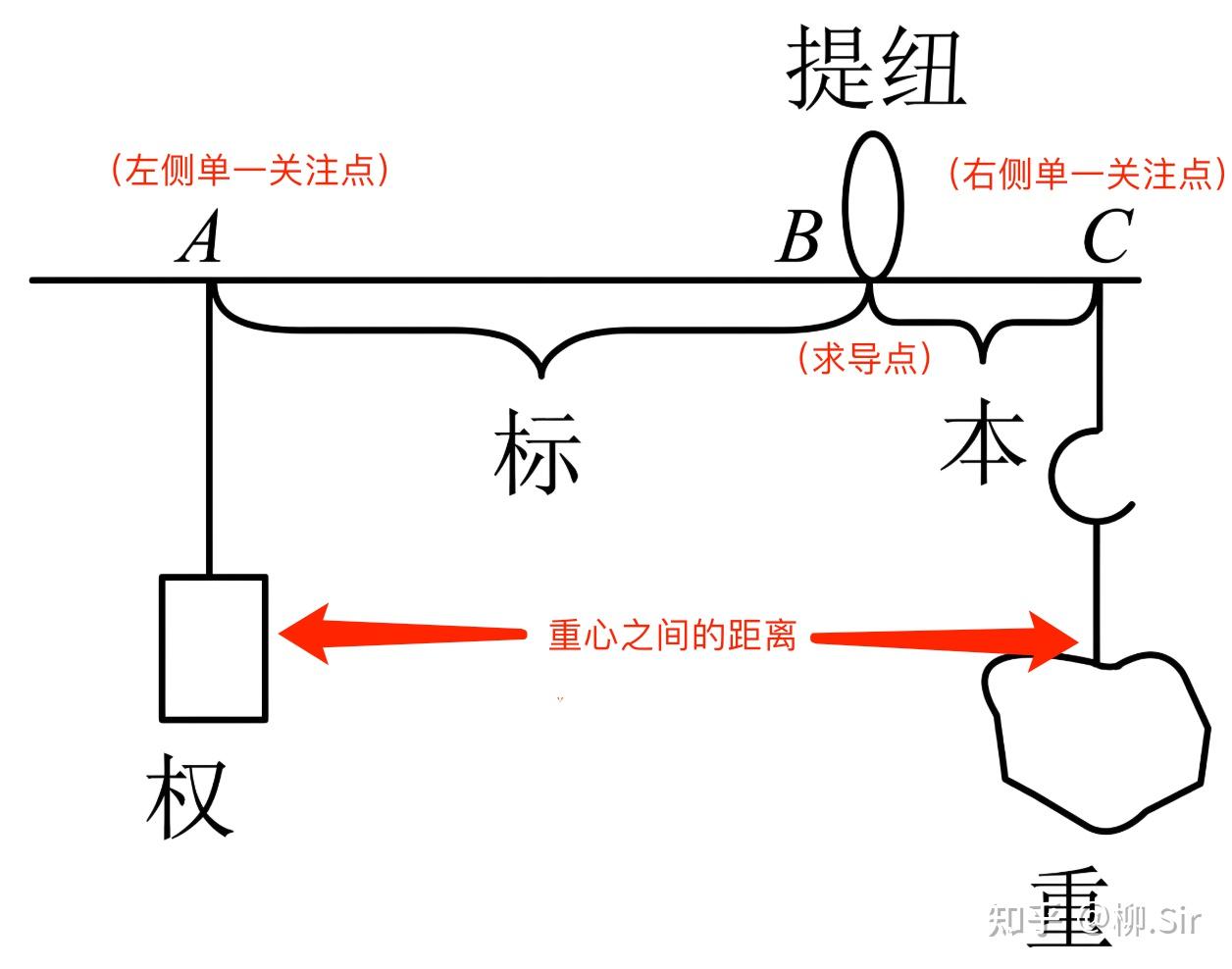
上面这一段的理解非常重要，我们已经开始通过利用 区间函数值计算导数 （即“积分计算微分”）的思想重新审视传统导数计算了，这也是更好理解Lanczos导数的核心。

现在我们来看Lanczos导数（论文详见此处），发现就很好理解了：

$fLD′(x0)=lim⁡W→032W3∫−WWtf(x0+t)dt=lim⁡W→032W3(∫0Wtf(x0+t)dt−∫0Wtf(x0−t)dt)=lim⁡W→0(∫0W2tW2f(x0+t)dt−∫0W2tW2f(x0−t)dt)2∫0W2tW2tdt最后两行是我写的\begin{aligned} f_{\mathrm{LD}}^{\prime}\left(x_0\right) & =\lim _{W \rightarrow 0} \frac{3}{2 W^3} \int_{-W}^W t f\left(x_0+t\right) \mathrm{d} t \\ & =\lim _{W \rightarrow 0} \frac{3}{2 W^3}\left(\int_0^W t f\left(x_0+t\right) \mathrm{d} t-\int_0^W t f\left(x_0-t\right) \mathrm{d} t\right) \\ & =\lim _{W \rightarrow 0} \frac{\left(\int_0^W \frac{2t}{W^2} f\left(x_0+t\right) \mathrm{d} t-\int_0^W \frac{2t}{W^2} f\left(x_0-t\right) \mathrm{d} t\right)}{2 \int_0^W\frac{2t}{W^2}t \mathrm{d}t} \quad 最后两行是我写的 \end{aligned}$

首先，用 $W$ （width）来表示左右观测区间的宽度，虽然区间宽度无限小。在求导点右侧 $x_0,x_0+W]$ 这个区间内，注意力分布是以 $\frac{2t}{W^2}$ 进行分布的，且区间内注意力总和 $∫0Ww(t)dt=∫0W2tW2dt=1\int_0^W w(t)dt = \int_0^W \frac{2t}{W^2}dt = 1$ ，其中 $t$ 是区间内关注点到求导点的距离；同样的，在求导点左侧 $x_0-W,x_0)$ 这个区间内，注意力是对称分布的，距离求导点距离为 $t$ 的点，注意力也为 $2tW2\frac{2t}{W^2}$ 。我之所以用注意力这个词，也是因为目前大模型太火了，说这个词更容易被人理解，在之前我就简单称之为“权重（weight）”，这也是 $w (t)$ 这个符号的来意。

这时候我们再看分母，不再是 $2 W$ ，而是 $\int_0^W\frac{2t}{W^2}t \mathrm{d}t$ ，其中很明显， $∫0W2tW2tdt\int_0^W\frac{2t}{W^2}t \mathrm{d}t$ 就是单侧区间注意力分布的重心位置（用到了一点物理学的知识），乘上2就成了左右重心之间的距离。

所以说， Lanczos导数的贡献核心，就是将传统导数中在左右分别关注一个点再进行“右减左”，扩展为了在左右分别关注一个小区间再进行“右减左” ，且这种关注一定是左右对称的（即距离求导点相同的距离的点关注度一样，关于为何要对称就不再数学解释了，直觉上就该左右对称，哲学上也该左右对称，否则大家距离都相等，你凭什么比我优越？）

Teruel进一步将Lanczos导数进行了推广（论文详见此处），将 $t$ 提换为 $t^k$ ，其中 $k$ 为正奇数 :

$fLD′(x0;k)=lim⁡W→0k+22Wk+2∫−WWtkf(x0+t)dt{k=2a+1∣a∈Z+}=lim⁡W→0k+22Wk+2(∫0Wtkf(x0+t)dt−∫0Wtkf(x0−t)dt){k=2a+1∣a∈Z+}=lim⁡W→0(∫0W(k+1)tkWk+1f(x0+t)dt−∫0W(k+1)tkWk+1f(x0−t)dt)2∫0W(k+1)tkWk+1tdt最后两行是我写的\begin{aligned} f_{\mathrm{LD}}^{\prime}\left(x_0 ; k\right) & =\lim _{W \rightarrow 0} \frac{k+2}{2 W^{k+2}} \int_{-W}^W t^k f\left(x_0+t\right) \mathrm{d} t \quad\left\{k=2 a+1 \mid a \in \mathbf{Z}^{+}\right\} \\ & =\lim _{W \rightarrow 0} \frac{k+2}{2 W^{k+2}}\left(\int_0^W t^k f\left(x_0+t\right) \mathrm{d} t-\int_0^W t^k f\left(x_0-t\right) \mathrm{d} t\right) \quad\left\{k=2 a+1 \mid a \in \mathbf{Z}^{+}\right\} \\ & =\lim _{W \rightarrow 0} \frac{\left(\int_0^W \frac{(k+1)t^k}{W^{k+1}} f\left(x_0+t\right) \mathrm{d} t-\int_0^W \frac{(k+1)t^k}{W^{k+1}} f\left(x_0-t\right) \mathrm{d} t\right)}{2 \int_0^W\frac{(k+1)t^k}{W^{k+1}}t \mathrm{d}t} \quad 最后两行是我写的 \end{aligned}$

对于拓展的Lanczos导数也很好理解了，无非就是将左右区间的注意力函数拓展为 $\frac{(k+1)t^k}{W^{k+1}}$ ，其他没什么变化。因为理解方式的不同（我的切入角度为“右减左”，Teruel是一气呵成），Teruel只写到第一行， $k$ 之所以为正奇数是因为他没有直接拆开写成“右减左”的形式，而是要求 $t$ 在积分过程中取负值的时候， $t^k$ 也是负数，以便满足“右减左”，所以 $k$ 不能为偶数。当拆开写到最后一行之后会发现， $k$ 取正偶数其实也没什么问题，不知道能否算我又把Lanczos导数进一步拓展了。

最后补充一句，Lanczos导数还有其他贡献，那就是对于有限个间断点，导数有定义了能计算了（因为其虽然不可导，但是可积），并且对于连续光滑函数，传统导数则和Lanczos导数保持一致（泰勒展开、洛必达法则等手段都可以证明）：

$fLD′(x0)=lim⁡W→032W3∫−WWtf(x0+t)dt=lim⁡W→032W3(∫0Wtf(x0+t)dt−∫0Wtf(x0−t)dt)=lim⁡W→032W3(∫0Wt(f(x0+t)−f(x0−t))dt)=lim⁡W→032W3(∫0Wt((f(x0)+tf′(x0)+O(t2))−(f(x0)−tf′(x0)+O(t2))dt)=lim⁡W→032W3(∫0W2t2f′(x0)+O(t3)dt)=lim⁡W→03f′(x0)2W3(∫0W2t2dt)=lim⁡W→03f′(x0)2W3⋅2W33=f′(x0)lim⁡W→032W3⋅2W33=f′(x0)\begin{aligned} f_{\mathrm{LD}}^{\prime}\left(x_0\right) & =\lim _{W \rightarrow 0} \frac{3}{2 W^3} \int_{-W}^W t f\left(x_0+t\right) \mathrm{d} t \\ & =\lim _{W \rightarrow 0} \frac{3}{2 W^3}\left(\int_0^W t f\left(x_0+t\right) \mathrm{d} t-\int_0^W t f\left(x_0-t\right) \mathrm{d} t\right) \\ &=\lim _{W \rightarrow 0} \frac{3}{2 W^3}\left(\int_0^W t (f\left(x_0+t\right) -f\left(x_0-t\right)) \mathrm{d} t\right) \\ &=\lim _{W \rightarrow 0} \frac{3}{2 W^3}\left(\int_0^W t((f(x_0)+tf^{\prime}(x_0)+O(t^2)) - (f(x_0)-tf^{\prime}(x_0)+O(t^2)) \mathrm{d} t\right) \\ &=\lim _{W \rightarrow 0} \frac{3}{2 W^3}\left(\int_0^W 2t^2f^{\prime}(x_0) + O(t^3) \mathrm{d} t\right) \\ &=\lim _{W \rightarrow 0} \frac{3f^{\prime}(x_0)}{2 W^3}\left(\int_0^W 2t^2 \mathrm{d} t\right) \\ &=\lim _{W \rightarrow 0} \frac{3f^{\prime}(x_0)}{2 W^3} ·\frac{2W^3}{3}\\ &=f^{\prime}(x_0)\lim _{W \rightarrow 0} \frac{3}{2 W^3} ·\frac{2W^3}{3}\\ &=f^{\prime}(x_0) \end{aligned}$

2. 从“特殊”到“一般”：从Lanczos导数到TD

首先，让我们将Lanczos导数中的 $2tW2\frac{2t}{W^2}$ 写为一般的注意力分布函数（权重函数） $w (t)$ ，其满足在观测区间 $(0, W]$ 内注意力和为1，即积分 $∫0Ww(t)dt=1\int_0^W w(t) \mathrm{d} t=1$ ；其次，为了实现“右减左”，在观测区间 $(0, W]$ 内的取值应该是正数，保证对应的右侧点减去左侧点；最后为了简化，直接定义非观测区间内无注意力，即取值为0：

${∫0Ww(t)dt=1w(t)>0t∈(0,W]w(t)=0t∈(−∞,0]∪(W,+∞)\begin{aligned} \left\{\begin{array}{ll} \int_0^W w(t) \mathrm{d} t=1 & \\ w(t)>0 & t \in(0, W] \\ w(t)=0 & t \in(-\infty, 0] \cup(W,+\infty) \end{array}\right. \end{aligned}$

当定义了注意力分布函数 $w (t)$ 之后，我们便能定义出TD（这只是一个名字，T可以粗浅理解为求导点在中间，肩膀上一左一右两条横线就像两个区间段，我要用一左一右两个区间辅助计算导数；D既是DaoShu的D，也是Derivative的D，即导数的意思。事实上“T”还有其他含义，这个等合集写完之后再聊）：

$fTD′(x0;w)≜lim⁡W→0∫0Wf(x0+t)w(t)dt−∫0Wf(x0−t)w(t)dt2∫0Wtw(t)dtf_{\mathrm{TD}}^{\prime}\left(x_0 ; w\right) \triangleq \lim _{W \rightarrow 0} \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t-\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t}$

不难看出，所谓的Lanczos导数就是TD取注意力函数 $\frac{2t}{W^2}$ 、 $\frac{(k+1)t^k}{W^{k+1}}$ 的特殊情况罢了。

$fTD′(x0;2tW2)=fLD′(x0)fTD′(x0;(k+1)tkWk+1)=fLD′(x0;k)\begin{aligned} f_{\mathrm{TD}}^{\prime}\left(x_0 ; \frac{2 t}{W^2}\right) & =f_{\mathrm{LD}}^{\prime}\left(x_0\right) \\ f_{\mathrm{TD}}^{\prime}\left(x_0 ; \frac{(k+1) t^k}{W^{k+1}}\right) & =f_{\mathrm{LD}}^{\prime}\left(x_0 ; k\right) \end{aligned}$

可证明， 对于光滑函数而言，TD等价于传统导数 ：

$=lim⁡W→0∫0W(f(x0)+tf′(x0)+O(t2))w(t)dt2∫0Wtw(t)dt=lim⁡W→0∫0W(2tf′(x0))w(t)dt2∫0Wtw(t)dt=f′(x0)lim⁡W→02∫0Wtw(t)dt2∫0Wtw(t)dt=f′(x0)\begin{aligned} f_{\mathrm{TD}}^{\prime}\left(x_0 ; w\right) & =\lim _{W \rightarrow 0} \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t-\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(f\left(x_0+t\right)-f\left(x_0-t\right)\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \quad \text { (Taylor's Formula) } \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(f\left(x_0\right)+t f^{\prime}\left(x_0\right)+O\left(t^2\right)\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(2 t f^{\prime}\left(x_0\right)\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =f^{\prime}\left(x_0\right) \lim _{W \rightarrow 0} \frac{2 \int_0^W t w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =f^{\prime}\left(x_0\right) \end{aligned}$

因为TD采用区间积分的计算方式，而积分运算具有线性属性：

$∫(af(x)+bg(x))dx=a∫f(x)dx+b∫g(x)dx\int (af(x) + bg(x)) \mathrm{d}x = a\int f(x) \mathrm{d}x + b \int g(x) \mathrm{d}x$ ，其中 $a, b$ 为常系数

可以推导出： $(af+bg)TD′=afTD′+bgTD′(af+bg)^{\prime}_{TD} = a f^{\prime}_{TD} + bg^{\prime}_{TD}$

更有意思的结论是，可以推导出求导的链式法则：

证明：对于光滑函数 $f$ 和 $g$ 由泰勒展开可知

$f(x0+t)=f(x0)+tf′(x0)+O(t2)g(x0+t)=g(x0)+tg′(x0)+O(t2)f(x0−t)=f(x0)−tf′(x0)+O(t2)g(x0−t)=g(x0)−tg′(x0)+O(t2)\begin{array}{l} f\left(x_0+t\right)=f\left(x_0\right)+t f^{\prime}\left(x_0\right)+O\left(t^2\right) \\ g\left(x_0+t\right)=g\left(x_0\right)+t g^{\prime}\left(x_0\right)+O\left(t^2\right) \\ f\left(x_0-t\right)=f\left(x_0\right)-t f^{\prime}\left(x_0\right)+O\left(t^2\right) \\ g\left(x_0-t\right)=g\left(x_0\right)-t g^{\prime}\left(x_0\right)+O\left(t^2\right) \end{array}$

则： $f(x0+t)g(x0+t)−f(x0−t)g(x0−t)=2t(f′g+g′f)+O(t2)f\left(x_0+t\right) g\left(x_0+t\right)-f\left(x_0-t\right) g\left(x_0-t\right)=2 t\left(f^{\prime} g+g^{\prime} f\right)+O\left(t^2\right)$

为此：

$(f⋅g)TD′=lim⁡W→0∫0Wf(x0+t)g(x0+t)w(t)dt−∫0Wf(x0−t)g(x0−t)w(t)dt2∫0Wtw(t)dt=lim⁡W→0∫0W(f(x0+t)g(x0+t)−f(x0−t)g(x0−t))w(t)dt2∫0Wtw(t)dt=lim⁡W→0(2∫0Wtw(t)dt)(f′g+g′f)+O(∫0Wt2w(t)dt)2∫0Wtw(t)dt=f′g+g′f=fTD′g+gTD′f\begin{aligned} (f \cdot g)_{\mathrm{TD}}^{\prime} & =\lim _{W \rightarrow 0} \frac{\int_0^W f\left(x_0+t\right) g\left(x_0+t\right) w(t) \mathrm{d} t-\int_0^W f\left(x_0-t\right) g\left(x_0-t\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(f\left(x_0+t\right) g\left(x_0+t\right)-f\left(x_0-t\right) g\left(x_0-t\right)\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\left(2 \int_0^W t w(t) \mathrm{d} t\right)\left(f^{\prime} g+g^{\prime} f\right)+O\left(\int_0^W t^2 w(t) \mathrm{d} t\right)}{2 \int_0^W t w(t) \mathrm{d} t} \\ & =f^{\prime} g+g^{\prime} f \\ & =f^{\prime}_{TD} g+g^{\prime}_{TD} f \end{aligned}$

看不懂没关系，知道结论就行： 传统导数运算的线性属性、链式求导法则，在TD之中依然存在 。

进一步我直接给出二阶TD导数的定义，它和传统的二阶导数形式类似，不再过多赘述，诸位知晓即可：

$f′′(x0)=lim⁡Δx→0f′(x0+Δx)−f′(x0)Δx=lim⁡Δx→0f(x0+Δx)−f(x0)Δx−f(x0)−f(x0−Δx)ΔxΔx=lim⁡Δx→0f(x0+Δx)+f(x0−Δx)−2f(x0)Δx2\begin{aligned} f^{\prime \prime}\left(x_0\right) &= \lim _{\Delta x \rightarrow 0} \frac{f^{\prime}\left(x_0+\Delta x\right)-f^{\prime}\left(x_0\right)}{\Delta x} \\ &= \lim _{\Delta x \rightarrow 0} \frac{\frac{f\left(x_0+\Delta x\right) - f(x_0)}{\Delta x}-\frac{f\left(x_0\right)-f(x_0-\Delta x)}{\Delta x}}{\Delta x} \\ &= \lim _{\Delta x \rightarrow 0} \frac{f(x_0+\Delta x) + f(x_0 - \Delta x) - 2f(x_0)}{\Delta x ^2} \end{aligned}$

$fTD′′(x0;w)≜lim⁡W→0∫0Wf(x0+t)w(t)dt+∫0Wf(x0−t)w(t)dt−∫0W2f(x0)w(t)dt∫0Wt2w(t)dt\\ f_{\mathrm{TD}}^{\prime \prime}\left(x_0 ; w\right) \triangleq \lim _{W \rightarrow 0} \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t+\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t- \int_0^W 2 f\left(x_0\right)w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t}$

同样可以通过泰勒展开证明，对于传统二阶导数存在时， 二阶TD导数和传统二阶导数等价 ：

$=f′′(x0)lim⁡W→0∫0Wt2w(t)dt∫0Wt2w(t)dt=f′′(x0)\begin{aligned} f_{\mathrm{TD}}^{\prime \prime}\left(x_0 ; w\right) & =\lim _{W \rightarrow 0} \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t+\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t- \int_0^W 2 f\left(x_0\right)w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(f\left(x_0+t\right)+f\left(x_0-t\right)-2 f\left(x_0\right)\right) w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t} \\ & =\lim _{W \rightarrow 0} \frac{\int_0^W\left(t^2 f^{\prime \prime}\left(x_0\right)+O\left(t^3\right)\right) w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t} \quad \text { (Taylor's Formula) } \\ & =f^{\prime \prime}\left(x_0\right) \lim _{W \rightarrow 0} \frac{\int_0^W t^2 w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t} \\ & =f^{\prime \prime}\left(x_0\right) \end{aligned}$

至此，我们已经成功地从两个点之间的“右减左”过渡到了两个区间的“右减左”，并且成功抽象出来了“注意力分布”这一概念。但是请注意，现在我们依然在区间无穷小的前提下讨论问题，还没有去除掉无穷小极限。接下来，就是一次“伟大”的变革， 去除掉lim无穷小极限符号这一桎梏，放开手脚开创一片新的天地 。

3. 从“束手束脚”到“放开拳脚”：从TD到TGD

同样的，TGD只是一个名字，“T”是说要用肩膀上左右两个区间内的函数值辅助表示计算中间点的导数值；"G"指代General，通用的，广义的，更一般的；"D"表示导数， TGD就是用左右相邻区间内的函数值辅助计算更具一般意义上的导数 。（虽然到现在，此导数的概念相较传统意义已经发生了变化）

TGD的两个公式很简单，就是在TD的基础上将无穷小的极限符号直接丢弃，并将观测区间 $W$ 的大小作为影响TGD计算值的一个变量。

$fTGD′(x0;w,W)≜∫0Wf(x0+t)w(t)dt−∫0Wf(x0−t)w(t)dt2∫0Wtw(t)dtfTGD′′(x0;w,W)≜∫0Wf(x0+t)w(t)dt+∫0Wf(x0−t)w(t)dt−∫0W2f(x0)w(t)dt∫0Wt2w(t)dt\begin{array}{c} f_{\mathrm{TGD}}^{\prime}\left(x_0 ; w, W\right) \triangleq \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t-\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t}{2 \int_0^W t w(t) \mathrm{d} t} \\ f_{\mathrm{TGD}}^{\prime \prime}\left(x_0 ; w, W\right) \triangleq \frac{\int_0^W f\left(x_0+t\right) w(t) \mathrm{d} t+\int_0^W f\left(x_0-t\right) w(t) \mathrm{d} t- \int_0^W 2 f\left(x_0\right)w(t) \mathrm{d} t}{\int_0^W t^2 w(t) \mathrm{d} t} \end{array}$

去除的是无穷小的极限符号，更是思想上的禁锢，这一步迈出去了，才算是正式走上了“积分计算微分”的道路。

正如同万千修真小说所言： 元婴之下，皆为蝼蚁，元婴出窍，灵魂与肉体分离，方才开始了真正的修行 。

第一篇中提到Lanczos导数中的注意力分布是错误的，错在何处？

TGD去除无穷小极限符号束缚后，是否需要受其他约束进一步控制？

TGD究竟能否可计算？是否简便？能否实用？

敬请下回分解，谢谢。

备注：

关于“导数公式中的分母是重心之间距离”的解读，在之前的各类文章中还没有遇到过（不知算不算首提），大家如有相关了解，欢迎私信或在评论区留言相互学习。
关于二阶TD和TGD的分母， $∫0Wt2w(t)dt\int^W_0 t^2w(t) \mathrm{d}t$ 是否具备物理上的或者数学上的其他含义，受限于知识暂不可知，如有了解，欢迎私信或在评论区留言相互学习。