Adaptive Graph Convolutional Network for Knowledge Graph Entity Alignment
面向知识图谱实体对齐的自适应图卷积网络
AGEA-EMNLP-2022
摘要
实体对齐(EA)旨在从不同知识图谱(KG)中识别等价实体,是知识图谱融合的基础任务。图卷积网络(GCN)已成为EA主流方法之一,其核心思想是:具有相似邻域结构的实体极可能对齐。但实体噪声邻居会传递无效信息、淹没等价特征,导致嵌入表示失真,最终降低EA性能。本文提出一种无训练参数的轻量级框架,适用于监督与非监督EA场景。基于Sinkhorn算法设计了伪等价实体可靠性度量方法,并提出自适应图卷积网络来抑制GCN中的邻居噪声。训练过程中网络动态更新关系三元组的自适应权重以弱化噪声传播。在基准数据集上的大量实验表明,本框架在监督与非监督设置下均优于现有最优方法。
1 引言
近年来,知识图谱(KG)作为组织存储数据的有效结构日益受到关注,已广泛应用于搜索引擎、问答系统、推荐系统等知识驱动应用。受数据源与构建方法限制,单一KG难以实现完美知识覆盖,这会影响知识驱动应用的性能。知识融合技术应运而生,通过捕捉多KG的差异性与互补性来弥补知识缺失并确保冗余度,从而提升KG的完备性。
实体对齐(EA)是知识融合的基础任务,旨在发现不同KG中的等价实体。图1展示了EA任务实例:存在法语KG和英语KG的局部。在监督EA设置中,等价实体对(Ville_de_séquoia,红木市)作为种子对齐已知,任务是从两个KG中发现其他等价实体对(如Comté_de_San_Mateo与圣马特奥县)。非监督EA设置中则无可用种子对齐。
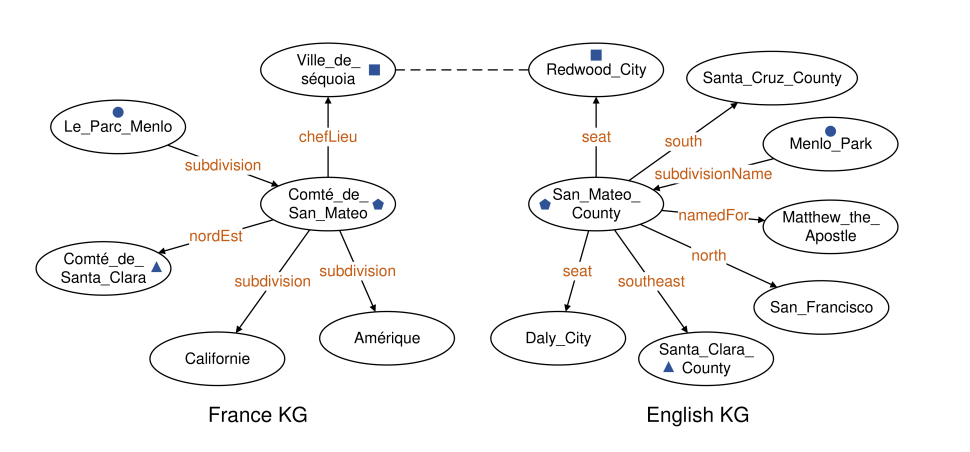
图1:EA任务示例。椭圆表示实体,有向箭头表示实体间关系,相同标记的实体为等价实体,虚线表示监督设置下的种子对齐。
当前神经方法已成为EA主导方法,其将两个KG的实体编码到统一向量空间,通过度量嵌入相似度实现对齐。现有神经方法可分为两类:(1)基于TransE的方法。TransE假设关系是头实体到尾实体的平移,将KG中所有关系和实体嵌入统一向量空间。基于TransE的EA方法通过语义信息学习实体嵌入,利用种子对齐构建跨KG关系三元组来连接两个图,然后在单KG和跨KG关系三元组上采用基于平移的KG嵌入模型。(2)基于GCN的方法。图卷积网络(GCN)通过聚合邻域节点信息生成节点级嵌入。基于GCN的EA方法通过KG信息扩散学习实体嵌入,对两个KG分别执行图卷积操作后,利用种子对齐通过边际损失或交叉熵损失对齐嵌入空间。
TransE与GCN在实体对齐(EA)中有效的原因在于先验知识:一对等价实体的各自邻域间可能存在多组等价实体对。等价实体分别向其邻接实体传递等价性。此外,对于来自不同知识图谱的实体,其邻域间包含的等价实体对越多,这两个实体等价的可能性越高。然而当前大多数研究忽视了EA中仍存在的一个关键挑战——由于等价实体也可能包含无贡献邻接点,GCN在消息传递过程中会引入额外噪声。这些噪声会淹没等价信息,导致实体嵌入不准确,最终降低EA性能。我们将此现象称为邻域噪声问题,这些无贡献连接称为噪声边。如图1所示,虽然实体Ville_de_séquoia(红杉市)、Le_Parc_Menlo(门洛公园)和Comté_de_Santa_Clara(圣克拉拉县)对对齐(Comté_de_San_Mateo, San_Mateo_County)有贡献,但实体Californie(加利福尼亚)和Amérique(美洲)引入的噪声会增大等价判定的难度。
为验证噪声边对EA性能的影响,我们基于真实对齐标注进行了探索性实验。图2展示了DBP15KZH-EN DBP15K{}_{\mathrm{{ZH}}\text{-EN }}DBP15KZH-EN 数据集上不同边设置下几种经典EA方法的性能表现,其中MTransE属于TransE类方法,GCN-Align、MRAEA、RREA和RAGA属于GCN类方法。移除所有噪声边后,两类方法的性能均显著提升。
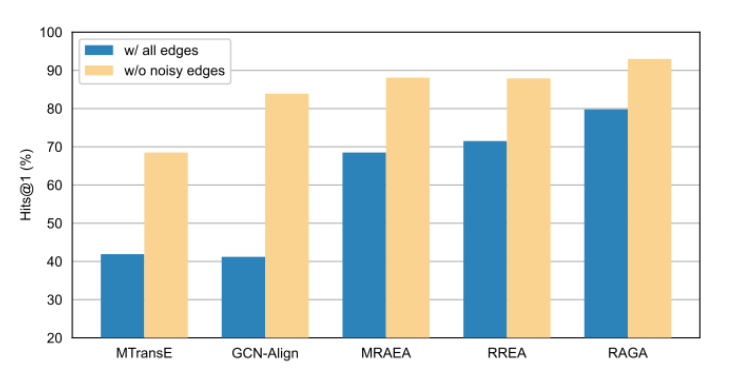
图2:不同边设置下的Hits@1对齐结果
然而实际场景中无法预先获取真实对齐标注。本文解决邻域噪声问题的核心思路是降低知识图谱中潜在噪声边的影响。我们采用Sinkhorn算法设计伪等价实体的可靠性度量,通过将该度量整合进GCN,提出自适应图卷积网络实体对齐框架(简称AGEA{\mathrm{{AGEA}}}AGEA)。训练过程中,该框架自动调整知识图谱关系三元组的权重以抑制噪声边的传播。本文主要贡献如下:
-
通过Sinkhorn算法设计伪等价实体度量标准,提出自适应边权重计算模块以解决邻域噪声问题
-
提出轻量化框架,在监督与非监督EA任务中均无需训练参数即可利用自适应边权重
-
在五个跨语言EA数据集上的实验表明,本框架以高效性和可解释性实现了最先进性能
2 问题定义
知识图谱形式化表示为KG=(E,R,T){KG} = \left( {\mathcal{E},\mathcal{R},\mathcal{T}}\right)KG=(E,R,T),其中E,R,T\mathcal{E},\mathcal{R},\mathcal{T}E,R,T分别表示实体集合、关系集合和关系三元组集合。关系三元组(h,r,t)由头实体h∈Eh \in \mathcal{E}h∈E、关系r∈Rr \in \mathcal{R}r∈R和尾实体t∈Et \in \mathcal{E}t∈E构成。
给定两个知识图谱KG1=(E1,R1,T1)K{G}_{1} = \left( {{\mathcal{E}}_{1},{\mathcal{R}}_{1},{\mathcal{T}}_{1}}\right)KG1=(E1,R1,T1)和KG2=(E2,R2,T2)K{G}_{2} = \left( {{\mathcal{E}}_{2},{\mathcal{R}}_{2},{\mathcal{T}}_{2}}\right)KG2=(E2,R2,T2),监督式EA任务定义为基于种子对齐集合A={(ei,ej)∣ei∈E1,ej∈E2,ei↔ej}\mathcal{A} = \left\{ {\left( {{e}_{i},{e}_{j}}\right) \mid {e}_{i} \in {\mathcal{E}}_{1},{e}_{j} \in {\mathcal{E}}_{2},{e}_{i} \leftrightarrow {e}_{j}}\right\}A={(ei,ej)∣ei∈E1,ej∈E2,ei↔ej}(其中↔\leftrightarrow↔表示等价关系)发现不同图谱间的等价实体;无监督EA任务目标相同但无需种子对齐A\mathcal{A}A。
3 相关工作
3.1 有监督实体对齐
基于TransE的方法采用TransE等基于翻译的知识图谱嵌入模型来学习实体嵌入。这些方法通过评分函数评估关系三元组的合理性来表示实体。MTransE将每个知识图谱的实体和关系编码到独立的嵌入空间,并通过转换矩阵对齐空间。JAPE将两个知识图谱的结构联合嵌入统一向量空间,并利用属性相关性进行优化。TransEdge根据头尾实体对情境化关系表示。BootEA通过自举方式扩展种子对齐来学习面向对齐的嵌入。这些方法虽能利用关系语义,但无法保留全局结构信息。
基于GCN的方法通过递归聚合邻居特征学习实体嵌入。由于更关注全局信息而非语义信息,需设计融合关系语义的网络结构。GCN-Align首次尝试用GCN编码邻域信息学习嵌入。MRAEA、RREA和RAGA基于图注意力网络融入关系语义。RDGCN和HGCN通过相邻实体表示近似关系语义。DGMC采用同步消息传递网络迭代重排软对应关系。SoTead通过求解最优传输问题实现全局实体匹配。
目前处理邻居噪声主要有三种方式:(1) 基于配对。GMM和EPEA生成成对实体嵌入,一定程度避免噪声问题。(2) 基于权重。NMN采用图采样策略识别训练中最具信息量的邻居。此类方法中边权重与实体嵌入相互影响,需高效模型架构。(3) 基于对齐。RNM通过邻域匹配增强训练后的实体对齐,其精度受邻居实体影响。我们的AGEA框架属于基于权重的方法,训练时利用伪等价实体计算自适应边权重,除实体嵌入外无需训练额外参数。
此外,还可利用多种附加信息提升对齐性能,如实体名称、实体描述、属性三元组、图像(Liu等人,2021a)和文本语料。鉴于实体名称在EA任务中的普遍性,本文仅使用实体名称获取初始嵌入。
3.2 无监督实体对齐
神经实体对齐方法虽性能优越,但主要依赖监督学习。这些监督方法需要种子对齐作为基础,而人工标注种子对齐成本高昂且实际场景中往往难以获取。为解决该问题,研究者提出了无监督实体对齐方法。EVA通过融合视觉知识与图结构信息,利用实体视觉相似性生成初始种子对齐,实现了完全无监督的解决方案。SoTead采用实体名称文本嵌入获取伪对齐。然而这些方法仅简单利用知识图谱的附加信息来生成训练用伪对齐。SEU假设两个知识图谱的实体具有同构性,将实体对齐问题转化为分配问题,并采用Sinkhorn算法进行对齐。SelfKG结合统一空间学习、相对相似度度量和自负面采样,实现了自监督实体对齐。在AGEA框架中,我们通过Sinkhorn算法定义伪对齐的可靠性,在SEU免训练对齐的基础上,将Sinkhorn算法整合到训练过程中。
4 研究方法
为实现高效训练并缓解过拟合,AGEA框架采用轻量级网络结构,除输入实体嵌入外不含可训练参数。如图3所示,网络输入包含两个知识图谱的关系三元组、种子对齐及初始实体嵌入。首先通过基础单图谱编码器(含加权图卷积网络和关系增强模块)获取实体嵌入,继而构建余弦相似度矩阵。每NA{N}_{A}NA个训练周期,通过计算自适应边权重更新关系三元组的自适应权重。训练过程中采用交叉熵函数计算监督损失和无监督损失,并通过反向传播算法更新输入实体的嵌入表示。
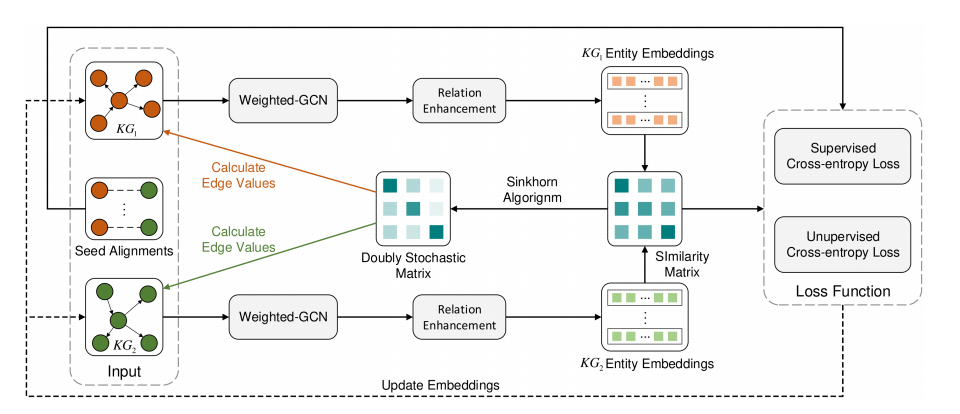
图3:AGEA的整体网络架构。
4.1 基础单图谱编码器
加权图卷积网络。采用LLL层加权GCN显式编码图谱结构信息。第lll层输入为X(l)={x1(l),x2(l),⋯ ,xn(l)}{\mathbf{X}}^{\left( l\right) } = \left\{ {{\mathbf{x}}_{1}^{\left( l\right) },{\mathbf{x}}_{2}^{\left( l\right) },\cdots ,{\mathbf{x}}_{n}^{\left( l\right) }}\right\}X(l)={x1(l),x2(l),⋯,xn(l)},其中nnn表示实体数量,xi(l){\mathbf{x}}_{i}^{\left( l\right) }xi(l)为第lll层实体ei{e}_{i}ei的输入向量。与节点分类任务不同,实体对齐更关注邻居实体传递的等价信息。AGEA中关系三元组的边权重已承担非等价信息过滤功能,因此采用权重归一化矩阵(而非拉普拉斯归一化矩阵)来提取邻居实体的等价信息。鉴于实体对齐任务易过拟合的特性,我们移除原始GCN中的可训练权重矩阵以缓解过拟合,并将实体映射至向量空间超球面使其距离适应余弦相似度度量。第lll层输出通过卷积运算获得:
X(l+1)=Norm(ReLU(Wˉ−1AˉX(l))),(1) {\mathbf{X}}^{\left( l + 1\right) } = \operatorname{Norm}\left( {\operatorname{ReLU}\left( {{\bar{W}}^{-1}\bar{A}{\mathbf{X}}^{\left( l\right) }}\right) }\right) , \tag{1} X(l+1)=Norm(ReLU(Wˉ−1AˉX(l))),(1)
其中Aˉ=A+I,A\bar{A} = A + I,AAˉ=A+I,A为邻接矩阵,KG,I\mathrm{{KG}},IKG,I为单位矩阵,Wˉ\bar{W}Wˉ表示实体邻接边权重求和的对角矩阵,Norm代表L2归一化。需注意的是GCN考虑关系三元组的双向边,训练初期所有边权重均初始化为1。最终输出为输入嵌入与各GCN层输出的拼接:
XGCN=[X(0)∥X(1)∥…∥X(L)].(2) {\mathbf{X}}^{\mathrm{{GCN}}} = \left\lbrack {{\mathbf{X}}^{\left( 0\right) }\begin{Vmatrix}{\mathbf{X}}^{\left( 1\right) }\end{Vmatrix}\ldots \parallel {\mathbf{X}}^{\left( L\right) }}\right\rbrack . \tag{2} XGCN=[X(0)X(1)…∥X(L)].(2)
关系增强。加权图卷积网络仅考虑实体间的邻接关系,忽略了实体间的关系类型。参照(Wu等,2019b)的方法,我们将关系类型融入实体表示以充分利用知识图谱的结构信息。具体而言,我们构建关系感知的实体嵌入但避免引入可训练网络参数。对于每个关系rrr,其表示rrr通过计算该关系所有头实体和尾实体输入嵌入的平均值获得。随后,关系感知的实体嵌入XR{\mathbf{X}}^{\mathrm{R}}XR由对应邻居关系的平均表示计算得出。最终,关系增强模块的输出X~\widetilde{\mathbf{X}}X通过拼接XGCN{\mathbf{X}}^{\mathrm{{GCN}}}XGCN与归一化后的XR{\mathbf{X}}^{\mathrm{R}}XR获得:
X~=[XGCN∥Norm(XR)].(3) \widetilde{\mathbf{X}} = \left\lbrack {{\mathbf{X}}^{\mathrm{{GCN}}}\parallel \operatorname{Norm}\left( {\mathbf{X}}^{\mathrm{R}}\right) }\right\rbrack . \tag{3} X=[XGCN∥Norm(XR)].(3)
4.2 自适应边权重计算
经过基础单知识图谱编码器处理后,我们获得实体嵌入X~\widetilde{\mathbf{X}}X。随后通过余弦相似度构建两个知识图谱间实体的相似度矩阵SSS。在计算自适应边权重前,我们首先引入伪等价实体可靠性度量指标,该指标同时用于自适应边权重计算和无监督损失函数。受(Mao等,2021)启发,我们对SSS应用Sinkhorn算法(Cuturi,2013)生成双随机矩阵Sˉ\bar{S}Sˉ:
Sˉ(0)=exp(TS) {\bar{S}}^{\left( 0\right) } = \exp \left( {TS}\right) Sˉ(0)=exp(TS)
Sˉ(m)=Normc(Normr(Sˉ(m−1))),(4) {\bar{S}}^{\left( m\right) } = {\operatorname{Norm}}_{c}\left( {{\operatorname{Norm}}_{r}\left( {\bar{S}}^{\left( m - 1\right) }\right) }\right) , \tag{4} Sˉ(m)=Normc(Normr(Sˉ(m−1))),(4)
Sˉ=limm→∞S(m) \bar{S} = \mathop{\lim }\limits_{{m \rightarrow \infty }}{S}^{\left( m\right) } Sˉ=m→∞limS(m)
其中TTT为温度系数,Normc{\mathrm{{Norm}}}_{c}Normc和Normr{\text{Norm}}_{r}Normr分别表示列向与行向的L1归一化。实际应用中,经过一定轮次运算可逼近Sˉ\bar{S}Sˉ。Sinkhorn算法时间复杂度为O(NSn2)O\left( {{N}_{S}{n}^{2}}\right)O(NSn2),其中NS{N}_{S}NS为迭代次数。该算法综合考虑双向对齐问题,Sˉ\bar{S}Sˉ每列每行元素之和均为1。在SEU(Mao等,2021)中,作者直接使用Sˉ\bar{S}Sˉ进行对齐。而我们将Sˉij{\bar{S}}_{ij}Sˉij视为KG1K{G}_{1}KG1中实体ei{e}_{i}ei与KG2K{G}_{2}KG2中实体ej{e}_{j}ej的全局相似度。
对于KG1K{G}_{1}KG1中每个实体ei{e}_{i}ei,我们取Sˉi:{\bar{S}}_{i : }Sˉi:最大值对应的实体作为其伪等价实体。同时,将该对伪等价实体的可靠性定义为最大值与次大值之差,记作c(Sˉi:)c\left( {\bar{S}}_{i : }\right)c(Sˉi:)。同理,对于KG2K{G}_{2}KG2中每个实体ej{e}_{j}ej,其对应伪等价实体对的可靠性为c(Sˉ:j)c\left( {\bar{S}}_{ : j}\right)c(Sˉ:j)。
为削弱相邻噪声的传播,我们利用两个相邻实体与其各自伪等价实体的可靠性来自适应计算边权重。图4展示了自适应边权重计算的示例。对于KG1K{G}_{1}KG1中的实体ei{e}_{i}ei,首先识别其在KG2K{G}_{2}KG2中的伪等价实体ej{e}_{j}ej。然后通过从双随机矩阵Sˉ\bar{S}Sˉ中提取ei{e}_{i}ei和ej{e}_{j}ej邻居对应的行列元素,构建邻居随机矩阵SˉNij{\bar{S}}^{{\mathcal{N}}_{ij}}SˉNij。对于从ei{e}_{i}ei指向ek{e}_{k}ek的边,将ei{e}_{i}ei的权重wi{w}_{i}wi定义为可靠性c(Sˉi:)c\left( {\bar{S}}_{i : }\right)c(Sˉi:),ek{e}_{k}ek的权重wk{w}_{k}wk定义为可靠性c(Sˉk:Nij)c\left( {\bar{S}}_{k : }^{{\mathcal{N}}_{ij}}\right)c(Sˉk:Nij)。最终计算对应的自适应边权重wik{w}_{ik}wik如下:
wik=max(wi,λ)⋅max(wk,λ),(5) {w}_{ik} = \max \left( {{w}_{i},\lambda }\right) \cdot \max \left( {{w}_{k},\lambda }\right) , \tag{5} wik=max(wi,λ)⋅max(wk,λ),(5)
其中λ\lambdaλ是控制实体权重最小值的超参数。通常,实体ei{e}_{i}ei与ej{e}_{j}ej之间的自适应边权重wik{w}_{ik}wik和wki{w}_{ki}wki是非对称的。我们取wik{w}_{ik}wik和wki{w}_{ki}wki的最大值作为双向边的权重。计算全部自适应边权重的时间复杂度为O(n2d)O\left( {{n}^{2}d}\right)O(n2d),其中ddd表示实体的平均度数。
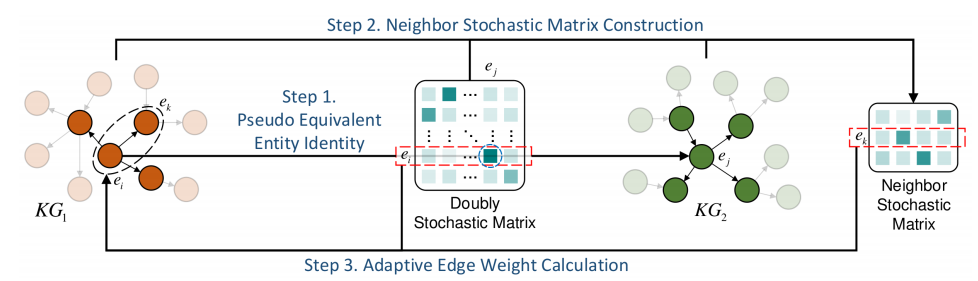
图4:KG1K{G}_{1}KG1中从ei{e}_{i}ei到ek{e}_{k}ek的自适应边权重wik{w}_{ik}wik计算过程。
4.3 训练与对齐
监督损失。在监督设置下,给定种子对齐A\mathcal{A}A。采用多类交叉熵损失函数,对于A\mathcal{A}A中的每个对齐(ei,ej)\left( {{e}_{i},{e}_{j}}\right)(ei,ej),将ej{e}_{j}ej视作正类,将Si:{S}_{i : }Si:中除ej{e}_{j}ej外前kkk个最大元素对应的实体作为负类集合Nik{\mathcal{N}}_{i}^{k}Nik。使用SSS中的值作为输入逻辑值,监督损失L\mathcal{L}L定义为:
L=−1∣A∣∑(ei,ej)∈Alogexp(Sij)∑ej′∈Nik∪{ej}⋅exp(Sij′). \mathcal{L} = - \frac{1}{\left| \mathcal{A}\right| }\mathop{\sum }\limits_{{\left( {{e}_{i},{e}_{j}}\right) \in \mathcal{A}}}\log \frac{\exp \left( {S}_{ij}\right) }{\mathop{\sum }\limits_{{{e}_{{j}^{\prime }} \in {\mathcal{N}}_{i}^{k} \cup \left\{ {e}_{j}\right\} }} \cdot \exp \left( {S}_{i{j}^{\prime }}\right) }. L=−∣A∣1(ei,ej)∈A∑logej′∈Nik∪{ej}∑⋅exp(Sij′)exp(Sij).
(6)
无监督损失。在无监督设置下,无种子对齐可用。利用KG1K{G}_{1}KG1中各实体计算的可靠性生成伪对齐集合A′{\mathcal{A}}^{\prime }A′。具体而言,对于每个实体ei{e}_{i}ei,若满足条件c(Sˉi:)>μc\left( {\bar{S}}_{i : }\right) > \muc(Sˉi:)>μ,则ei{e}_{i}ei与其对应的伪等价实体构成伪对齐。将式6中的A\mathcal{A}A替换为A′{\mathcal{A}}^{\prime }A′来计算无监督损失。
对齐。训练完成后,在实体向量空间的超球面上,具有相似邻居的实体相互靠近,反之则被推远。由此可获得两个知识图谱间实体的最终相似度矩阵。与SEU类似,我们应用Sinkhorn算法进行对齐。
5 实验设置
5.1 数据集
我们在两组常用数据集上评估所提框架,包括五对知识图谱:(1) DBP15K(Sun等人,2017年),包含三对跨语言知识图谱:中英(ZH-EN)、日英(JA-EN)和法英(FR-EN),每数据集含15,000个对齐实体对;(2) SRPRS,其数据集更稀疏,度分布更接近真实场景。选取两对跨语言图谱(英法和英德)进行评估,每数据集同样包含15,000个对齐实体对。表1展示了数据集统计信息。
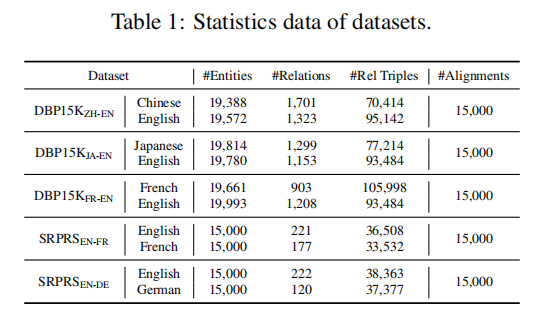
5.2 评估指标
参照(Wang等, 2020)的方法,我们采用H@k(命中率@K)和MRR(平均倒数排名)来衡量实体对齐(EA)的性能。在监督学习设定下,多数先前研究使用30%{30}\%30%的对齐数据作为训练集,70%{70}\%70%作为测试集,并报告测试集上的最佳结果。为保证规范性和公平比较,我们抽取5%测试数据用于验证,同时报告全部70%{70}\%70%测试数据的结果。值得注意的是,相较于多数先前研究的评估方法,我们的评估方式会导致结果偏低。在无监督设定下,我们随机抽取5%5\%5%的对齐数据进行验证,并在全量数据上报告对齐结果。本方法所有报告结果均为十次不同随机种子实验的平均值。
5.3 对比方法
为全面评估本框架,我们同时比较了监督式EA方法和无监督基线方法。为确保公平性,我们尽量避免与那些需要除实体名称外额外信息的方法进行比较。对比的监督基线包括:基于TransE的方法——MTransE、JAPE、BootEA和TransEdge;基于GCN的方法——GCN-Align、MRAEA、HGCN、DGMC、NMN、RAGA、RNM、EPEA以及SoTead。所有无监督基线均为基于GCN的方法,包括EVA、SEU、SelfKG和SoTead。
上述方法中,BootEA、TransEdge和MRAEA采用迭代或自举策略实现半监督EA;JAPE、EPEA、EVA和SelfKG分别利用了属性三元组、字符级实体名称、实体图像和实体描述。这些策略和附加信息均未在我们的框架中使用。此外,我们添加了仅采用初始实体嵌入和余弦相似度的朴素方法NameE。
5.4 实现细节
参照(Wu等, 2019b)的方法,我们将非英语实体名称翻译为英语,并通过预训练的Glove构建初始实体嵌入。我们使用Pytorch实现AGEA框架,并采用多进程技术加速自适应边权重和邻居感知对齐的计算。实验在配备Intel® Xeon® CPU E5-2699 v3 @ 2.30GHz处理器、128GB内存和NVIDIA GeForce RTX 2080Ti显卡的工作站上进行。
训练过程中,每个对齐的负样本类别数kkk设为20,计算自适应边权重的间隔周期数NA{N}_{A}NA为15。当计算自适应边权重时,Sinkhorn算法的温度系数TTT设为50,算法迭代次数NS{N}_{S}NS为10,实体权重最小值λ\lambdaλ为0.2。在无监督设定下,构建伪种子对齐的阈值μ\muμ设为0.5。
6 实验结果
6.1 主要结果
表2展示了所有方法的总体结果。几乎所有可比结果均引自原始论文,部分缺失数据来自综述文献(Zhao等, 2022)。由于SEU提供了仅使用与我们相同实体名称信息的对齐结果,我们从其消融研究中引用了这些数据。
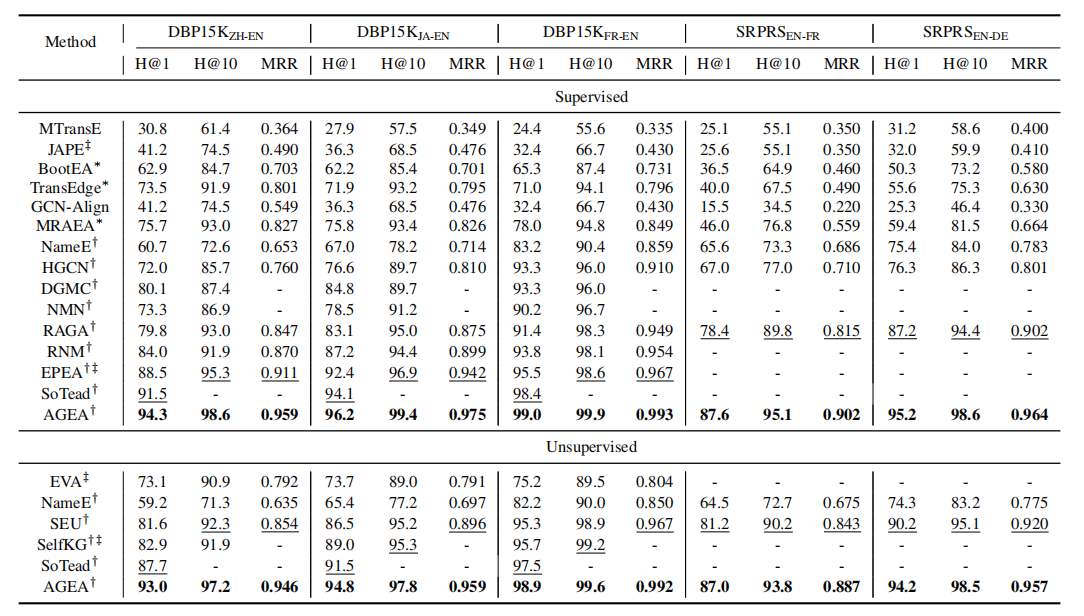
表2:总体结果。标*的方法采用迭代或自举策略;标†{}^{ \dagger }†的方法使用实体名称和预训练Glove获取初始实体嵌入;标‡{}^{ \ddagger }‡的方法使用本框架AGEA未采用的额外信息。监督/无监督设置下的最优(次优)结果以粗体(下划线)标注。
与监督方法的对比。总体而言,基于图卷积网络(GCN)的方法优于基于TransE的模型,因其能捕捉全局信息并广泛利用实体名称和预训练语言模型构建初始实体嵌入。在所有基线方法中,RAGA、EPEA和SoTead分别在部分数据集上取得最佳结果。相较于上述前沿方法,我们的AGEA框架在所有数据集上均实现显著提升。相比NameE,AGEA通过训练和邻居感知对齐机制有效融合初始实体嵌入与知识图谱结构信息,最终使H@1指标提升15.8%-33.6%。
与无监督方法的对比。在DBP15K数据集上,AGEA较最强基线SoTead将H@1指标提升1.4%-5.3%。值得注意的是,即使与多数监督方法相比,我们的模型仍具优势,这验证了可靠性度量与无监督损失函数的有效性。需特别说明的是,SEU是一种免训练方法。SEU与AGEA均利用Sinkhorn算法取得优异效果,揭示了该算法的优越性。
不同度数实体的性能对比。如图5所示,我们通过额外实验探究不同度数实体的表现。从数据集角度看,相较于DBP15 KZH−EN{15}{\mathrm{\;K}}_{\mathrm{{ZH}} - \mathrm{{EN}}}15KZH−EN,SRPRSEN−FR{\mathrm{{SRPRS}}}_{\mathrm{{EN}} - \mathrm{{FR}}}SRPRSEN−FR上大量低度数实体导致信息传播受阻,增加了任务难度。从模型角度看,尽管经典神经方法整体优于朴素NameE,但对低度数实体的处理远逊于高度数实体。而我们的AGEA框架在低度数实体上表现更优,这得益于自适应边权使低度数实体的反向传播梯度更为纯净。
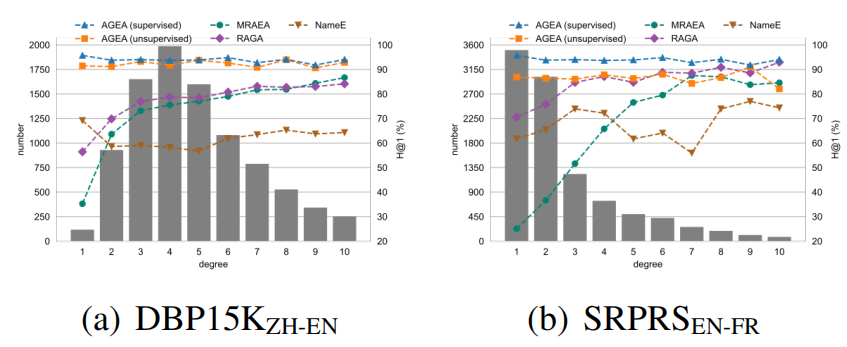
图5:不同度数实体的H@1\mathrm{H}@1H@1结果。
6.2 时间效率
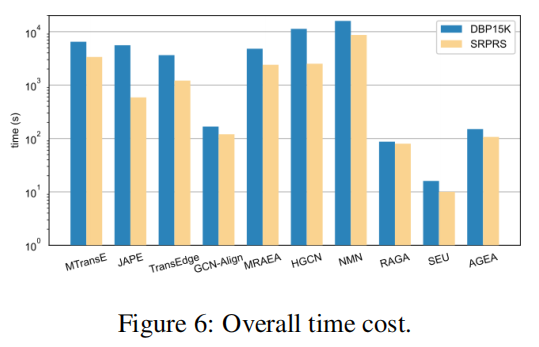
为全面评估,我们运行原始论文提供的源代码,分别获取DBP15K和SRPRS数据集上的平均运行时间。图6展示了各方法的平均耗时(含训练与测试时间)。可见免训练方法SEU是最快基线,在DBP15K上约16秒,SRPRS上约10秒。得益于轻量级网络和多进程加速,我们的模型在基于训练的方法中耗时近乎最短——DBP15K约120秒,SRPRS约100秒。
6.3 消融研究
我们对监督版AGEA进行深入消融研究。如表3所示,实现了多个AGEA变体。表中Ada、Sink和Train分别表示是否采用自适应边权计算、Sinkhorn对齐算法和训练过程。NameE仅使用初始实体嵌入和余弦相似度。所有模块均有贡献,其中Sinkhorn算法与训练过程是基础且贡献最大。无训练时,相较NameE,我们的框架使H@1提升12.6%-23.4%。仅结合训练后的加权GCN与Sinkhorn算法,即可在DBP15 KZH−EN{15}{\mathrm{\;K}}_{\mathrm{{ZH}} - \mathrm{{EN}}}15KZH−EN上实现93.6%{93.6}\%93.6%的H@1结果,优于表2中最佳基线SoTead。此外,无论是否使用Sinkhorn算法,加入自适应边权计算后精度均有提升,印证了该模块的有效性。
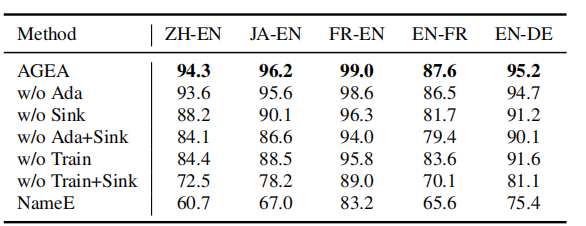
表3:H@1\mathrm{H}@1H@1不同变体的实验结果
6.4 超参数分析
图7展示了超参数分析结果
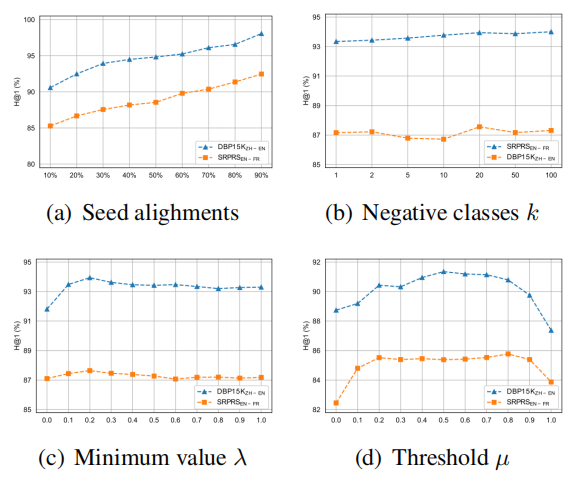
种子对齐比例。更多的种子对齐能为不同知识图谱间提供更多桥梁信息。随着种子对齐比例增加,监督式AGEA的准确率持续提升
负类数量kkk。负类数量kkk用于平衡实体对的等价信息与差异信息。较小的kkk会导致差异信息不足,而较大的kkk会淹没等价信息。随着kkk增加,监督式AGEA在DBP15K上的性能缓慢提升,在SRPRS上则略有波动。
实体权重最小值λ\lambdaλ。计算自适应边权重时,实体权重最小值λ\lambdaλ意味着对伪等价实体可靠性的修正,这会依次影响实体和边的权重。当λ\lambdaλ为1时,所有边权重均为1;若其值为0,则大量边权重将趋近于0,导致结构信息利用不足。权衡之下,AGEA在λ\lambdaλ约为0.2时表现最佳。
阈值μ\muμ。阈值μ\muμ控制无监督EA中伪对齐的精度。当μ\muμ较小时,构建的伪对齐过少会导致训练不足;反之若μ\muμ过大,伪对齐精度下降将导致实体嵌入不准确。实践中μ\muμ取0.5较为适宜。
6.5 案例研究
我们在图8中展示了一个可视化训练后自适应边权重的案例,图例与图1保持一致。通过在边上标注权重值并以透明度表示权重强度,可见对于等价实体对(Comté_de_San_Mateo, San_Mateo_County),其邻域等价实体对(Ville_de_séquoia, Redwood_City)、(Le_Parc_Menlo, Menlo_Park)和(Comté_de_Santa_Clara, Santa_Clara_County)对应的边权重较大。此外由于(Ville_de_séquoia, Redwood_City)是种子对齐,其边权重略高于另外两个等价实体对。这些现象验证了我们自适应边权重计算模块解决邻域噪声问题的可行性。
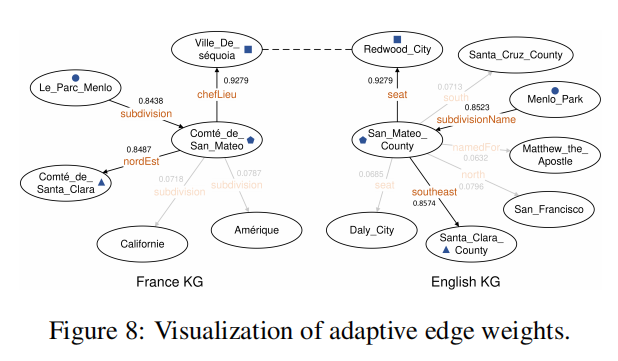
图8:自适应边权重可视化
7 结论
本工作针对EA任务中的邻域噪声问题,提出了轻量高效的AGEA框架。该框架核心是自适应边权重计算模块,并结合Sinkhorn算法融入基于GCN的EA框架,表现出优异性能。在五个数据集上的实验表明,AGEA在监督和无监督设置下均优于现有方法,兼具高效性与可解释性。
局限性
AGEA框架中自适应边权重计算模块、无监督损失函数和最终对齐均基于Sinkhorn算法,但该算法应用于EA任务的前提是将EA转化为分配问题(Mao等人,2021),这要求每个实体在另一知识图谱中必有对应实体。我们的框架在理想数据集DBP15K和SRPRS上表现良好,但对于两图谱重叠度低的数据集可能失效。该局限被多数前人研究忽视,由此催生了悬空实体对齐这一新研究方向(Luo等人,2022)。
