模运算常见定律

模运算（Modular Arithmetic）在数学和计算机科学中广泛应用，以下是其核心定律和性质：

---

1. ​基本定义​

若整数 a 除以正整数 m 得到余数 r，则记作：

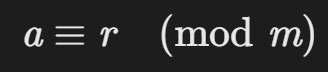
≡​ 表示同余关系（Congruence Relation）
即 a=km+r，其中 0≤r<m，k 为整数。

---

2. ​同余性质​

• ​自反性​：a≡a(mod  m)
• ​对称性​：若 a≡b(mod  m)，则 b≡a(mod m)
• ​传递性​：若 a≡b(mod  m) 且 b≡c(mod  m)，则 a≡c(mod  m)

---

3. ​算术运算定律​

• ​加法​：
• ​减法​：
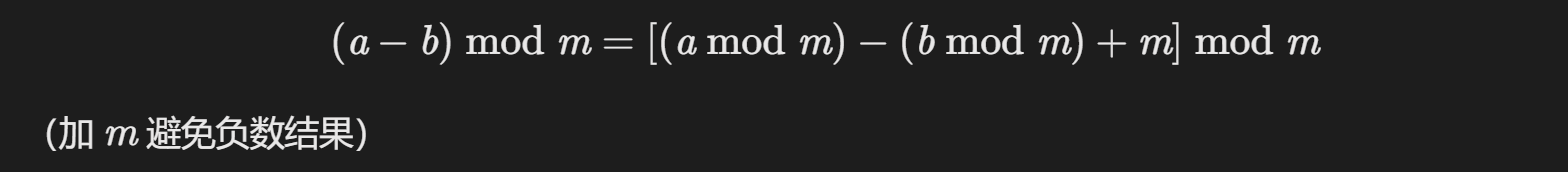
• ​乘法​：
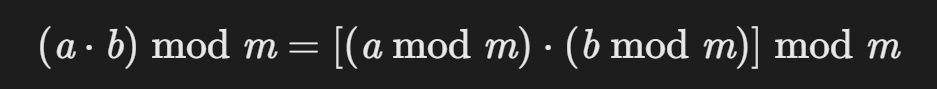
• ​幂运算​：

---

4. ​分配律与结合律​

• ​分配律​：(a+b)⋅c≡a⋅c+b⋅c(mod  m)
• ​结合律​：(a⋅b)⋅c≡a⋅(b⋅c)(mod  m)

---

5. ​逆元（Modular Inverse）​​

若 a 与 m 互质（即 gcd(a,m)=1），则存在唯一整数 x 满足：

记作，可通过扩展欧几里得算法求解。

---

6. ​费马小定理（素数模数）​​

若 p 为素数且 a 不被 p 整除：

推论：a−1≡ap−2(modp)。

---

7. ​中国剩余定理（CRT）​​

若模数 m1​,m2​,…,mk​ 两两互质，则同余方程组：

⎩⎨⎧​x≡a1​(modm1​)x≡a2​(modm2​)⋮x≡ak​(modmk​)​

有唯一解模 M=m1​m2​⋯mk​。

---

8. ​欧拉定理（推广费马小定理）​​

若 gcd(a,m)=1，则：

aϕ(m)≡1(modm)

其中 ϕ(m) 是欧拉函数，表示小于 m 且与 m 互质的正整数个数。

---

9. ​模运算的周期性​

• 幂运算的周期：若 gcd(a,m)=1，则 akmodm 的周期是 ϕ(m) 的约数。
• 例如：a≡b(modm)⇒an≡bn(modm)。

---

应用场景

• ​密码学​：RSA、Diffie-Hellman 密钥交换。
• ​哈希函数​：取模保证输出范围。
• ​算法优化​：大数运算的快速取模（如快速幂取模）。

理解这些定律有助于高效处理离散数学、加密算法和编程中的模运算问题。