当前位置：首页 > news >正文

【沧海拾昧】微分先行PID与中间微分反馈控制

news 2025/7/24 6:33:54

#C0404

沧海茫茫千钟粟，且拾吾昧一微尘

——《沧海拾昧集》@CuPhoenix

【阅前敬告】 沧海拾昧集仅做个人学习笔记之用，所述内容不专业不严谨不成体系 【如有问题必是本集记录有谬，切勿深究】

前言

微分先行 PID 算法和 中间微分反馈 算法是两种针对纯时延过程进行补偿的常规控制方案，但目前许多互联网资料中将两种方法进行了混淆。事实上，两种控制方法的结构与效果是存在一定差异的。

本文将简要介绍两种控制方法的基本结构，并给出相应推导的位置式公式和增量式公式。

本文用到的软件环境是：

MATLAB R2019b

一、微分先行PID算法

1、基本概念

微分先行控制方案与传统 PID 控制方案相比，对于减小超调量有更显著的表现，这是因为虽然二者的特征方程完全相同，但微分先行控制方案的闭环传递函数比 PID 控制方案少一个零点。
在这里插入图片描述

PI + D 系统框图和微分先行控制方案系统框图

可以看出，这种传统的 PID 控制方案中的微分环节的输入是对偏差做了比例积分运算后的值，不能真正的直接对被控参数的变化速度进行校正，因此克服动态超调的作用是有限的。但如果将微分环节直接作用于反馈通道中，就可以较大程度的增加微分作用克服超调的能力，也就是所谓的微分先行控制。

必须指出的是，微分先行控制方案中，微分环节的输出信号包括了 被控参数，以及 被控参数的变化速度，并将其作为测量值输入比例积分调节器中。目前许多资料中所给出的将被控参数的变化速度直接与 PI 调节器的输出值相减实际上是中间微分控制方案，而不是微分先行控制方案。

2、仿真框图

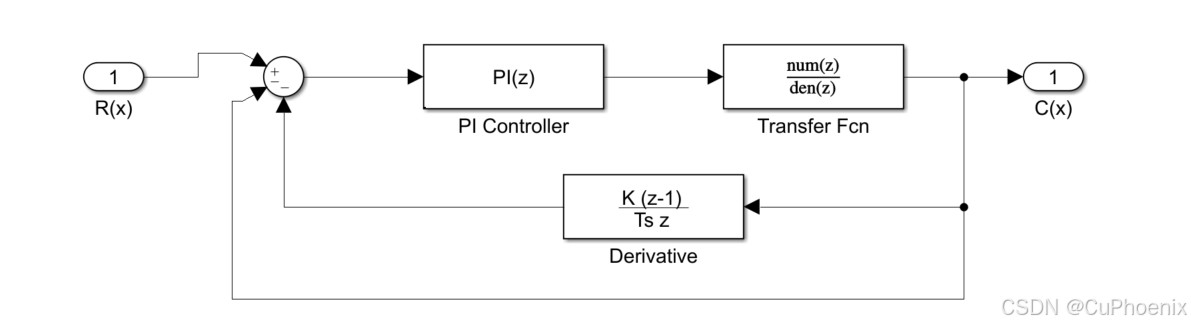
在这里插入图片描述

微分先行控制方案仿真框图

3、离散公式

位置式离散公式

按照框图，微分先行控制方案离散形式公式为：
$out(t)=Kp⋅E(k)+Ki⋅T⋅∑j=0kE(j)out(t)=K_p\cdot E(k)+K_i\cdot T \cdot\sum^k_{j=0}E(j)$
其中 $E(k)=r(x)−c(x)−ddtc(x)=e(k)−Kd⋅c(k)−c(k−1)TE(k)=r(x)-c(x)-\dfrac{d}{dt}c(x)=e(k)-K_d\cdot\dfrac{c(k)-c(k-1)}{T}$ ；

增量式离散公式

由位置式离散公式有：
$out(k)=Kp⋅E(k)+Ki⋅T⋅∑j=0kE(j)out(k−1)=Kp⋅E(k−1)+Ki⋅T⋅∑j=0k−1E(j)out(k)=K_p\cdot E(k)+K_i\cdot T \cdot\sum^k_{j=0}E(j) \\ out(k-1)=K_p\cdot E(k-1)+K_i\cdot T \cdot\sum^{k-1}_{j=0}E(j)$

两式相减，即为：
$Δout=Kp⋅[E(k)−E(k−1)]+Ki⋅T⋅E(k)\Delta out=K_p\cdot[E(k)-E(k-1)]+K_i\cdot T\cdot E(k)$

将 $E(k)=e(k)−Kd⋅c(k)−c(k−1)TE(k)=e(k)-K_d\cdot\dfrac{c(k)-c(k-1)}{T}$ 和 $E(k−1)=e(k−1)−Kd⋅c(k−1)−c(k−2)TE(k-1)=e(k-1)-K_d\cdot\dfrac{c(k-1)-c(k-2)}{T}$ 代入上式，即得：

$Δout=Kp⋅[e(k)−Kd⋅c(k)−c(k−1)T−e(k−1)+Kd⋅c(k−1)−c(k−2)T]+Ki⋅T⋅[e(k)−Kd⋅c(k)−c(k−1)T]\Delta out=K_p\cdot[e(k)-K_d\cdot\frac{c(k)-c(k-1)}{T}-e(k-1)+K_d\cdot\frac{c(k-1)-c(k-2)}{T}]+K_i\cdot T\cdot [e(k)-K_d\cdot\frac{c(k)-c(k-1)}{T}]$

化简后有：

$Δout=Kp⋅[e(k−1)−e(k)]−Kp⋅KdT[c(k)−2c(k−1)+c(k−2)]+Ki⋅T⋅e(k)−Ki⋅Kd[c(k)−c(k−1)]\Delta out=K_p\cdot[e(k-1)-e(k)]-\frac{K_p\cdot K_d}{T}[c(k)-2c(k-1)+c(k-2)]+K_i\cdot T\cdot e(k)-K_i\cdot K_d[c(k)-c(k-1)]$

二、中间微分反馈算法

1、基本概念

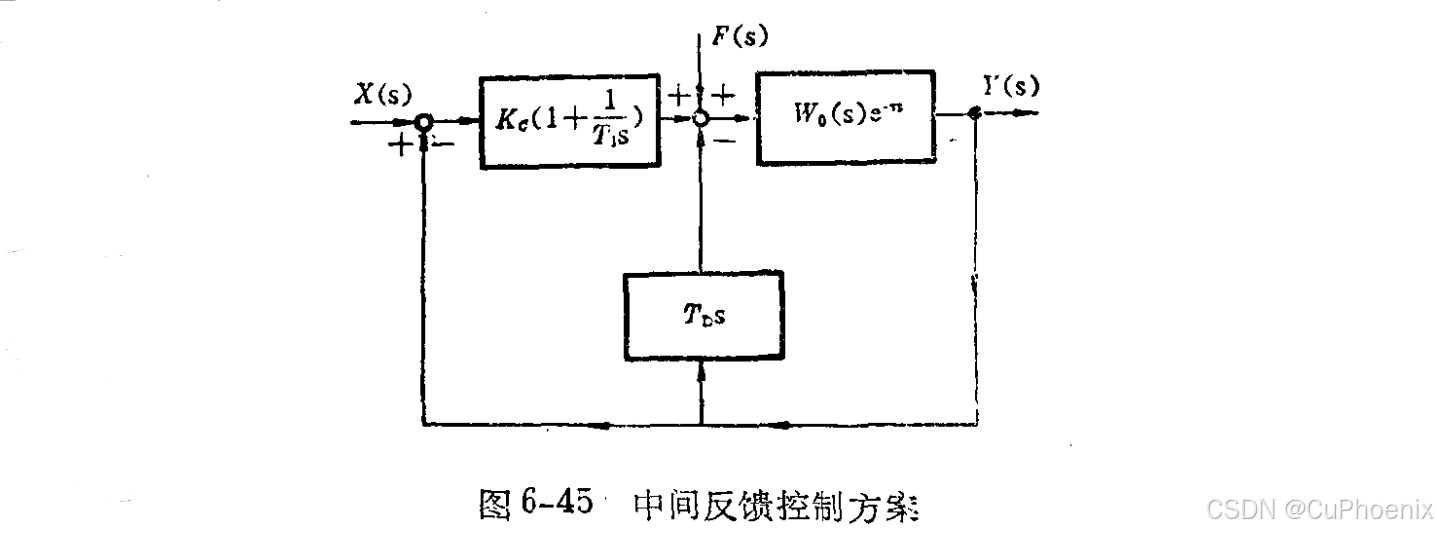
在这里插入图片描述

中间微分反馈控制方案系统框图

与微分先行方案的思想类似，中间微分反馈方法也是将微分环节移出，以增强对动态超调的克服作用。由图可见，在中间微分反馈方案中，微分作用是独立的，能在被控参数变化时及时根据其变化大小起附加校正的作用，其微分校正作用 与 PI 调节器的输出信号无关，且只在动态时其作用。

中间微分反馈控制方案的零点与原 PI 控制器的零点相同，但主导极点相比原 PI 控制方案离 $jωj\omega$ 轴较远，因此衰减较快，过渡过程时间较短。

2、仿真框图

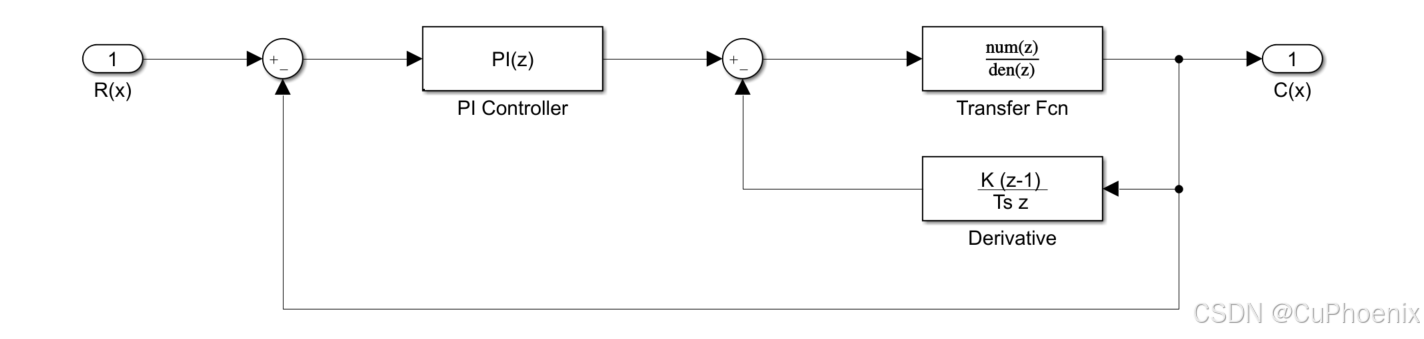
在这里插入图片描述

中间微分反馈控制方案仿真框图

3、离散公式

位置式离散公式

按照框图，中间微分反馈方案连续形式公式为：
$out(t)=Kp⋅e(t)+Ki⋅∫0te(t)dt−Kd⋅ddtc(t)out(t)=K_p\cdot e(t)+K_i\cdot\int^t_0e(t)dt-K_d\cdot\frac{d}{dt}c(t)$

离散化后为：
$out(k)=Kp⋅e(k)+Ki⋅T⋅∑j=0ke(j)−Kd⋅c(k)−c(k−1)Tout(k)=K_p\cdot e(k)+K_i\cdot T \cdot\sum^k_{j=0}e(j)-K_d\cdot\frac{c(k)-c(k-1)}{T}$
其中 $e (k) = r (k) - c (k)$ ;

增量式离散公式

由位置式离散公式有：
$out(k)=Kp⋅e(k)+Ki⋅T⋅∑j=0ke(j)−Kd⋅c(k)−c(k−1)Tout(k−1)=Kp⋅e(k−1)+Ki⋅T⋅∑j=0k−1e(j)−Kd⋅c(k−1)−c(k−2)Tout(k)=K_p\cdot e(k)+K_i\cdot T \cdot\sum^k_{j=0}e(j)-K_d\cdot\frac{c(k)-c(k-1)}{T} \\ out(k-1)=K_p\cdot e(k-1)+K_i\cdot T \cdot\sum^{k-1}_{j=0}e(j)-K_d\cdot\frac{c(k-1)-c(k-2)}{T}$

两式相减，即为：
$Δout=Kp⋅[e(k)−e(k−1)]+Ki⋅T⋅e(k)−KdT⋅[c(k)−2c(k−1)+c(k−2)]\Delta out=K_p\cdot[e(k)-e(k-1)]+K_i\cdot T\cdot e(k)-\frac{K_d}{T}\cdot[c(k)-2c(k-1)+c(k-2)]$