当前位置：首页 > news >正文

数据结构之【排序】(直接插入排序、希尔排序)

news 2025/7/25 11:33:58

1.直接插入排序

1.1直接插入排序的思想

1.2直接插入排序的代码逻辑：

1.3 直接插入排序图解

1.4单趟排序代码(单个元素的排序逻辑)

1.5完整排序代码

1.6直接插入排序的时间复杂度与空间复杂度

1.7直接插入排序的优势

2.希尔排序(缩小增量排序)

2.1希尔排序的思想

2.2希尔排序的代码逻辑

2.3希尔排序图解

2.4单单趟排序代码(对于特定的gap的一组元素的排序)

2.5单趟排序代码(对于特定的gap的分组排序)

2.5.1一组排好序再排另一组

2.5.2 根据元素的所在组进行直接插入排序

2.6完整排序代码

2.6.1一组排好序再排另一组

2.6.2 根据元素的所在组进行直接插入排序

2.7希尔排序的时间复杂度与空间复杂度

所有排序的实现皆以升序为例

1.直接插入排序

1.1直接插入排序的思想

直接插入排序的思想就是将待排序的数插入到一组有序的数中

就像打扑克牌摸牌阶段，我们一张一张摸牌并整理有序的过程就是直接插入排序的过程

1.2直接插入排序的代码逻辑：

创建 end 变量，初始化为有序数组中最后一个数的下标

创建 tmp变量，初始化为待排序的数值

然后将 tmp变量与 end位置的数 从后向前依次比较，按需要(升降序)挪动与存放数据

1.3 直接插入排序图解

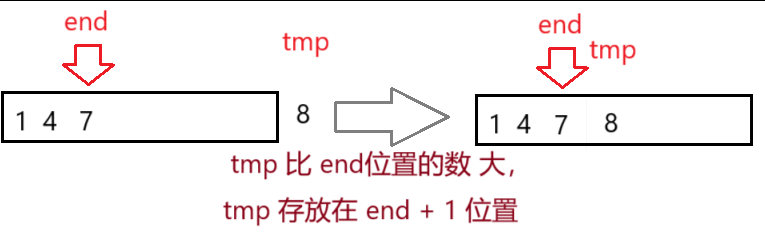
如果 tmp 比 end位置的数大，tmp 存放在 end + 1 位置

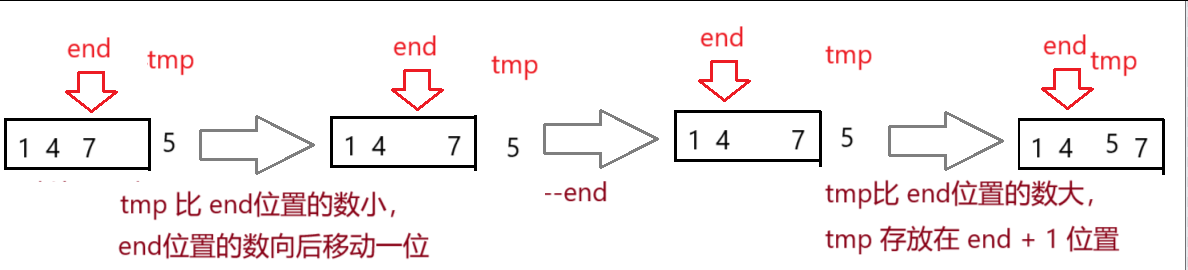
如果 tmp 比 end位置的数小，先将end位置的数向后移动一位，再 --end

然后继续将 tmp 与 end位置的数从后向前依次比较

如果 tmp 比 end位置的数大，tmp 存放在 end + 1 位置

(1) 依次比较，这显然是一个循环

(2) tmp可能比所有值都小，即 end 可能小于0 (数组下标的角度)，这可以作为循环结束条件

(3) 实现正确的情况下， tmp 永远存放在 end + 1 位置

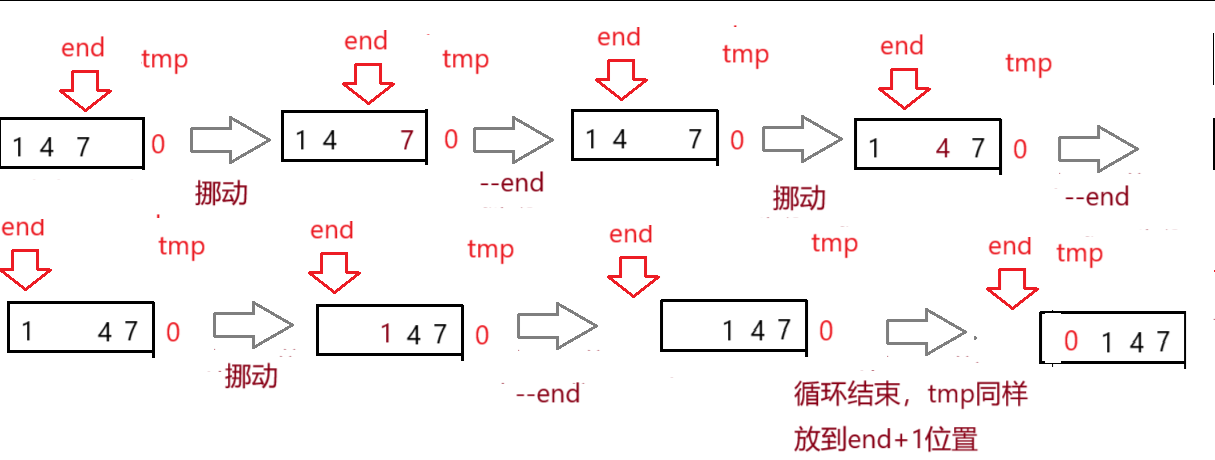
1.4单趟排序代码(单个元素的排序逻辑)

int end;
int tmp;
while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else break;
}
a[end + 1] = tmp;

tmp 比 end位置的数小 就一直挪动数据并--end

tmp 比 end位置的数大就跳出循环

因为我们知道 (实现正确下) tmp 永远放在 end + 1 位置

选择在循环外面控制 tmp 存放的位置可以解决 end<0 与 end >= 0两种情况

end >= 0，即 tmp 不存放在数组中首元素的位置

end < 0，即 tmp 比所有数组元素都要小，不断--end，直到循环结束，最终放在第一个位置

1.5完整排序代码

void InsertSort(int* a, int n){ for(int i = 0; i < n - 1; ++i){int end = i;int tmp = a[i + 1];while (end >= 0){if (tmp < a[end]){a[end + 1] = a[end];--end;}else break;}a[end + 1] = tmp;}
}

在单趟排序的基础上控制end与tmp即可完整代码

一个数我们可以看作是有序的，所以 end初始值应为0，tmp初始值为数组中的第二个数

一趟比较完毕，前两个数有序了，end位置往后挪，tmp被赋值为下一个数

这显然也是一个循环........

1.6直接插入排序的时间复杂度与空间复杂度

直接插入排序的最坏情况就是输入数组完全逆序，

假设数组有N个元素，即

第1次插入操作（从第2个元素（索引1）开始插入）：前1个已排序元素一共后移1次

第2次插入操作：前2个已排序元素一共后移2次

第3次插入操作：前3个已排序元素一共后移3次

.........

第 N - 1 次插入操作：前N - 1 个已排序元素一共后移N - 1 次

那么移动总次数就是（(N - 1）* N）/ 2

所以时间复杂度就是 O(N^2）

直接插入排序创建的变量只有i、end、tmp，变量的数量固定，所有操作均在原数组上完成

所以空间复杂度为O(1)

1.7直接插入排序的优势

元素集合越接近有序，直接插入排序算法的时间效率越高

2.希尔排序(缩小增量排序)

2.1希尔排序的思想

希尔排序的思想就是通过分组直接插入排序和缩小增量(gap)的操作改进普通的直接插入排序

2.2希尔排序的代码逻辑

将间隔大小为gap(初始值一般为n/2、n/3+1)的数组元素看作一组，每组进行直接插入排序，然后缩小gap(n/2/2、(n/3+1)/3+1)，再进行直接插入排序，缩小gap再排序.....

一直到gap为1的直接插入排序完成截止

显然这是循环套循环，因为gap不断缩小而对于每个具体的gap来说又需要进行直接插入排序

2.3希尔排序图解

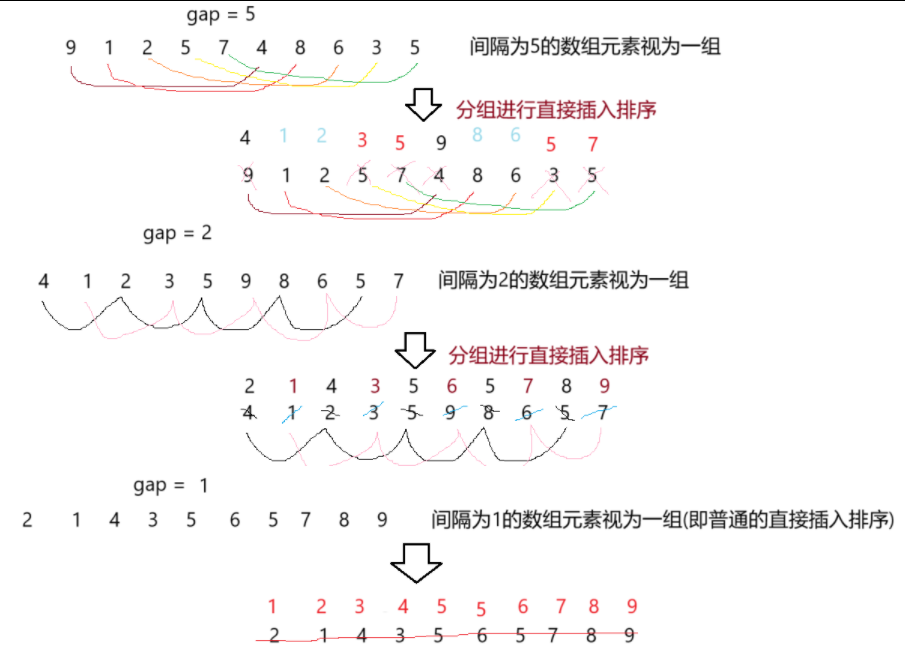
循环开始，gap初始值为n/2，直接插入排序完成后，gap /= 2，再一次直接插入排序完成后，gap/=2，此时gap缩小至1，此次直接插入排序完成后，数组有序

gap必须缩小至1，才能保证数组有序

gap也可以是 gap = gap / 3 + 1，+1是为了gap最终可缩小至1

gap /= 2不用+1 因为式子本身可以确保gap缩小至1

2.4单单趟排序代码(对于特定的gap的一组元素的排序)

        int gap;int end;int tmp;while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else    break;}a[end + gap] = tmp;}
}

相对于直接插入排序，单单趟的变化简单来说就是移动间隔从1变为了gap

2.5单趟排序代码(对于特定的gap的分组排序)

2.5.1一组排好序再排另一组

int gap;
gap /= 2;
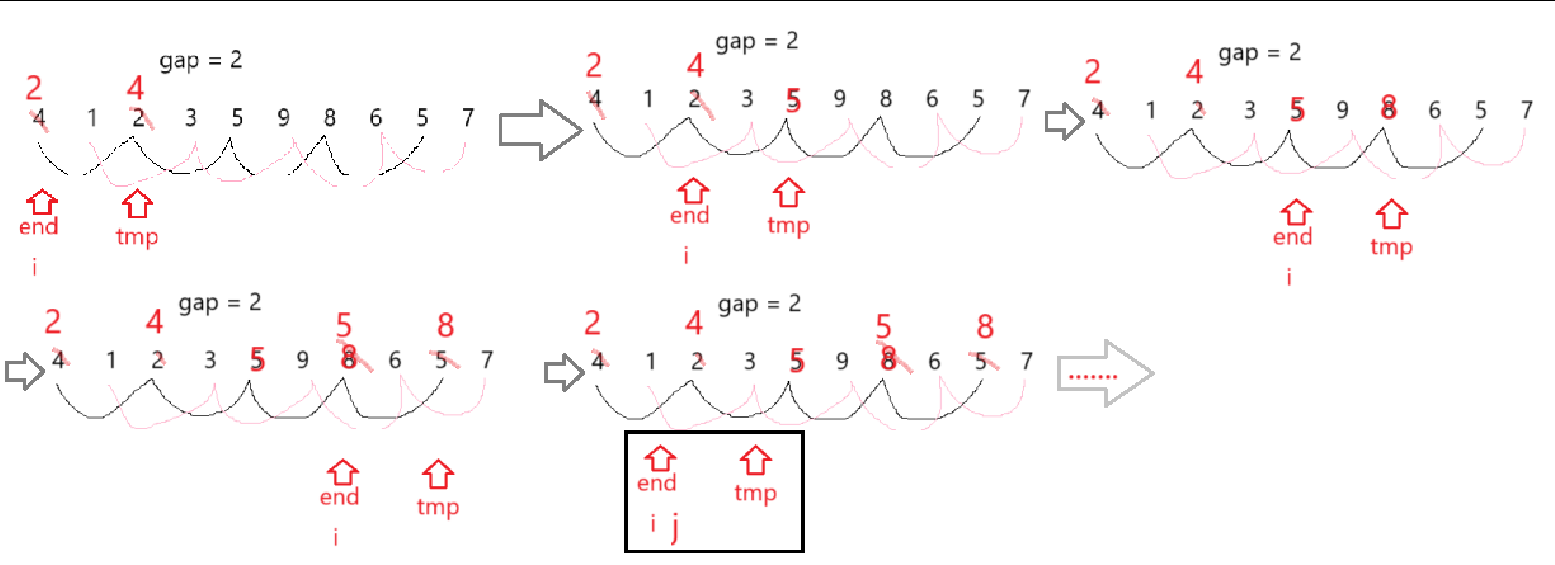
for(int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else    break;}a[end + gap] = tmp;}
}

内层for循环控制的是特定的某一组数组元素的end与tmp的变化值

两者间隔为gap，end初始值为i，tmp为其后gap个位置的值，所以i+gap<n，即i < n - gap

因为是先排好一组再排另外一组，所以需要 i+=gap

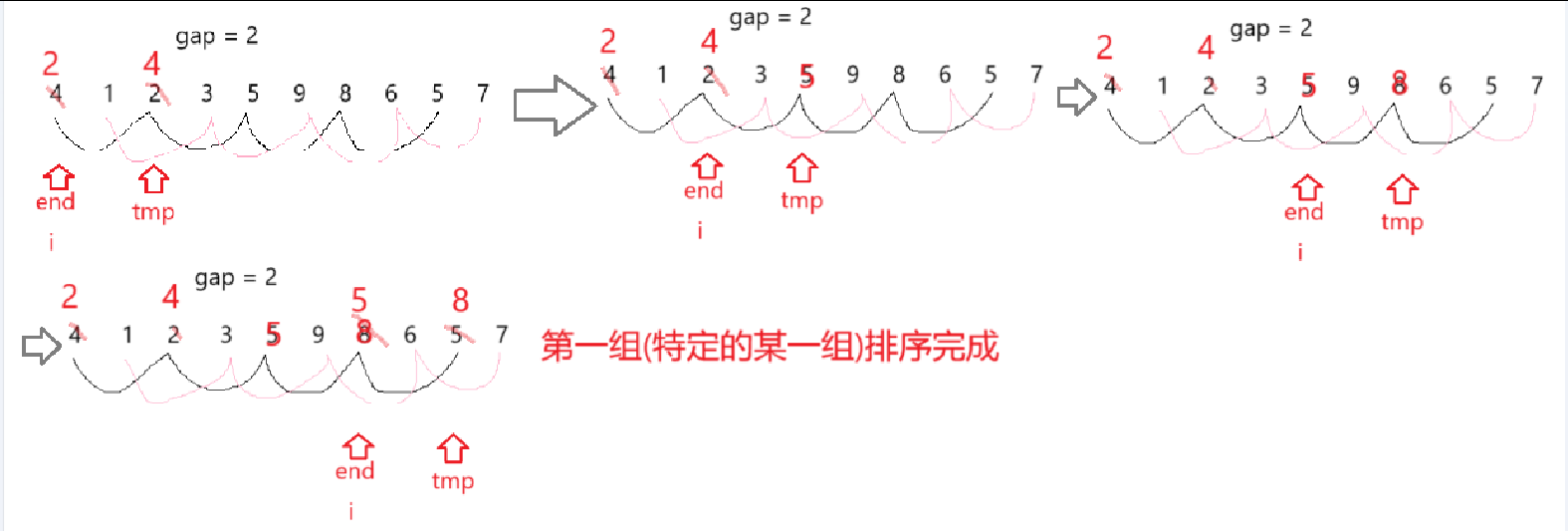
外层for循环控制的是每一组数组元素的end的初始值

假设数组一共有n个元素，将间隔大小为gap的数组元素视为一组，那么每一组数组元素的end的初始值一定 大于等于零小于gap(下标从零开始)

2.5.2 根据元素的所在组进行直接插入排序

int gap;
gap /= 2;
for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else    break;}a[end + gap] = tmp;
}

遍历数组元素，根据元素的所在组进行直接插入排序

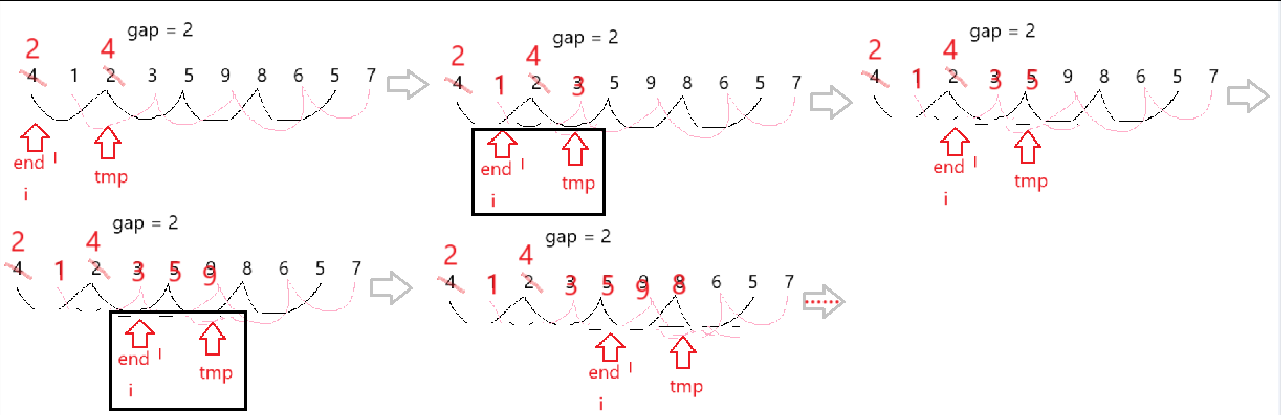
for循环控制的是数组元素的end与tmp的变化值

两者间隔为gap，end初始值为i，tmp为其后gap个位置的值，所以i+gap<n，即i < n - gap

通过 ++i 就可实现遍历数组并根据元素的所在组进行直接插入排序的操作

2.6完整排序代码

2.6.1一组排好序再排另一组

void ShellSortUp2(int* a, int n)
{int gap = n;while (gap > 1){gap /= 2;for(int j = 0; j < gap; ++j){for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else    break;}}a[end + gap] = tmp;}}}
}

通过将gap初始化为n，并将gap大于1作为循环结束条件，可以避免单个数的排序现象

再在循环内部将gap/2，也不迟

2.6.2 根据元素的所在组进行直接插入排序

void ShellSortUp1(int* a, int n)
{int gap = n;while(gap > 1){gap /= 2;for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[i + gap];while (end >= 0){if (tmp < a[end]){a[end + gap] = a[end];end -= gap;}else    break;}a[end + gap] = tmp;}}
}