多校2+多校1的遗珠
题目意思:
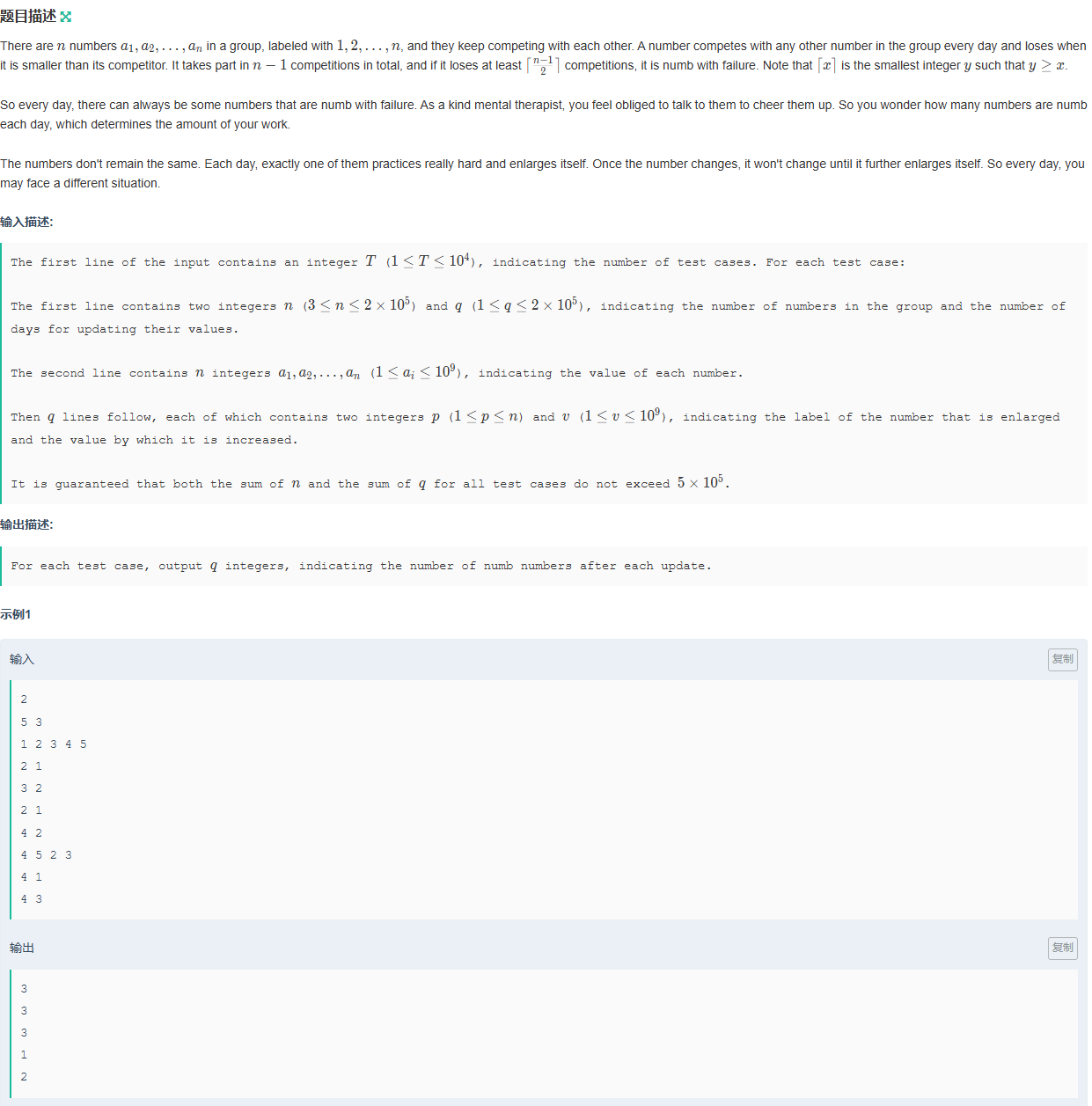
给定一个数组,找出除了自己外ai,其他数aj比自己大的个数(定义为cz75),统计每个数的cz75个数大于n/2的数量。
思路:
用红黑树或者树状数组进行维护原先数组,然后在通过离散化进行二分求解。
但其实还有一种用map的极限过题的写法。
首先用map统计每个数的个数,answer维护没有改变数组中数字前的答案。
随后对于读进来的数字进行滚动改变答案,最后对改变数组中的数字进行特判即可。
用时1900ms多,差点超。
#include<bits/stdc++.h>
using namespace std;
#define int long long
map<int,int>p;
inline void solve(){p.clear();int n;cin>>n;int nn;cin>>nn;vector<int>ac(n+1);for(int i=1;i<=n;i++){cin>>ac[i];p[ac[i]]++;}//p放每个数字的个数int answer=0;auto it=p.begin();//用it来表示最小不满足条件的数字while(it!=p.end()&&n-answer-it->second>=n/2){answer+=it->second;//answer维护it=next(it);}for(int i=1;i<=nn;i++){int x,y;cin>>x>>y;//判定删去的数字和it之间的关系,是否对answer有影响if(ac[x]<it->first)answer--;//旧值p[ac[x]]--;ac[x]+=y;if(ac[x]<it->first)answer++;//新值p[ac[x]]++;while(it!=p.end()&&n-answer-it->second>=n/2){//最后更新一遍it的位置answer+=it->second;it= next(it);}cout<<answer<<endl;}
}
signed main(){ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;cin>>t;while(t--)solve();
}贴一份官方的代码
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
using namespace std;
using namespace __gnu_pbds;
using pll = pair<long long, int>;
// 定义基于红黑树的有序统计树(ordered statistics tree)
// 可以高效地进行插入、删除、查找排名等操作
using ost = tree<pll, null_type, less<pll>, rb_tree_tag,//升序lesstree_order_statistics_node_update>;
int main() {ios::sync_with_stdio(false);cin.tie(nullptr);int Tcs;cin>>Tcs;while (Tcs--) {int n, q;cin >> n >> q;vector<long long> a(n);ost tr; for (int i = 0; i < n; ++i) {cin >> a[i];// 插入元素到树中,pair 的格式为 (值, 索引)tr.insert({a[i], i});}const int k = n / 2;for (int i = 0; i < q; ++i) {int p;long long v;cin >> p >> v; --p; // 从树中删除旧值tr.erase({a[p], p});// 更新数组中的值a[p] += v;// 将新值插入树中tr.insert({a[p], p});// 找到第 k 大的值(即树中排名为 n - k 的元素)// 因为树是按升序排列的,所以第 k 大的值是排名为 n - k 的元素long long ans = tr.find_by_order(n - k)->first;// 计算小于 T 的元素数量(即 T 的排名 - 1)// order_of_key 返回的是严格小于给定键的元素数量int cnt = tr.order_of_key({ans, -1}); // 使用 -1 作为索引确保不会匹配到实际元素cout << cnt << "\n";}}return 0;
} 
题目意思:
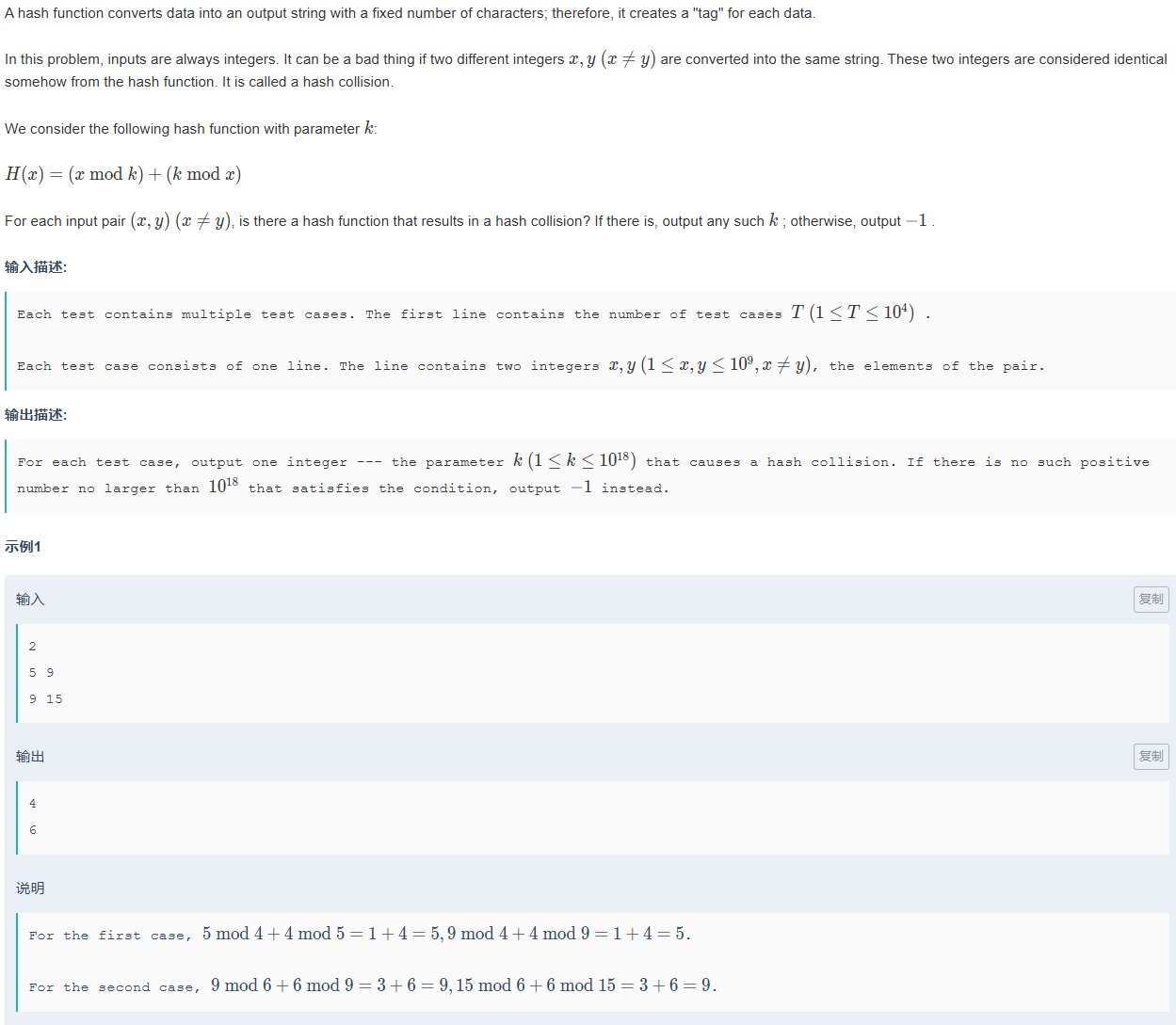
找出一个数k满足x%k+k%x=y%k+k%y,如果没有输出-1。
思路:
题目中k的取值范围给我们一种提示,k可以取值1,故直接大胆猜测,所有成对的数字k=1一定满足,事实也是如此。x%1=0 1%x=1
但是当x,y之间有1存在的时候条件就不满足,特判即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline void solve(){int x,y;cin>>x>>y;if(x>y)swap(x,y);if(x!=1)cout<<1<<endl;else cout<<-1<<endl;
}
signed main(){int t;cin>>t;while(t--)solve();
}
题目意思:
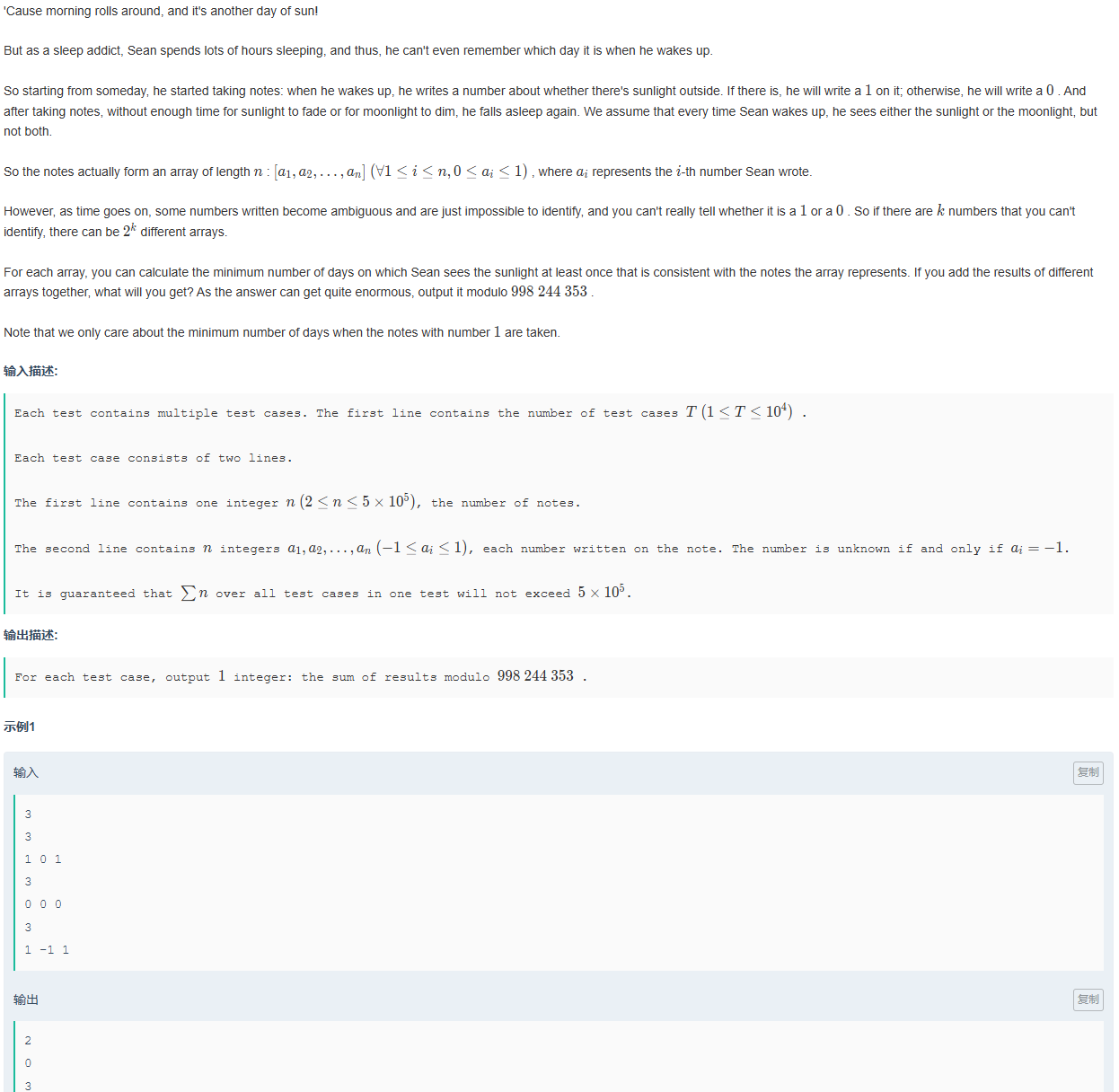
给定一个数组-1可以替换成01任意一个,在我们数组前面加上0,计算01作为子数组出现的次数。
思路:
首先我们先手写几个样例
01111
01
这两的贡献其实是一样的,不难发现其实就是找01串,-1可以替代0和1。
此时我们想每一对01串的贡献,如果这对01串内部没有出现-1,那么此时的贡献就是所有-1可变。
(2的-1个数次方)
如果01串内部出现了-1,减去此时-1的个数即可。
特判第一个数字是1的情况 此时贡献是所有-1可变。
#include<bits/stdc++.h>
using namespace std;
const int mod=998244353;
#define int long long
int kuai(int a,int b){int sum=1;while(b){if(b&1)sum=(sum*a)%mod;a=(a*a)%mod;b>>=1;}return sum;
}
inline void solve(){int n;cin>>n;int sum=0;vector<int>a(n);for(int &x:a){cin>>x;if(x==-1)sum++;//统计-1个数}int answer=0;if(a[0]==1||a[0]==-1){int f=a[0]==-1;answer=kuai(2,sum-f)%mod;}//特判第一个数字是1的情况for(int i=1;i<n;i++){//找01串int dang=(a[i]==1||a[i]==-1);int qian=(a[i-1]==0||a[i-1]==-1);if(!dang||!qian)continue;int f=(a[i]==-1)+(a[i-1]==-1);answer=(answer+kuai(2,sum-f))%mod;//剩下-1可变的数量}cout<<answer<<endl;
}
signed main(){int t;cin>>t;while(t--)solve();
}
题目意思:
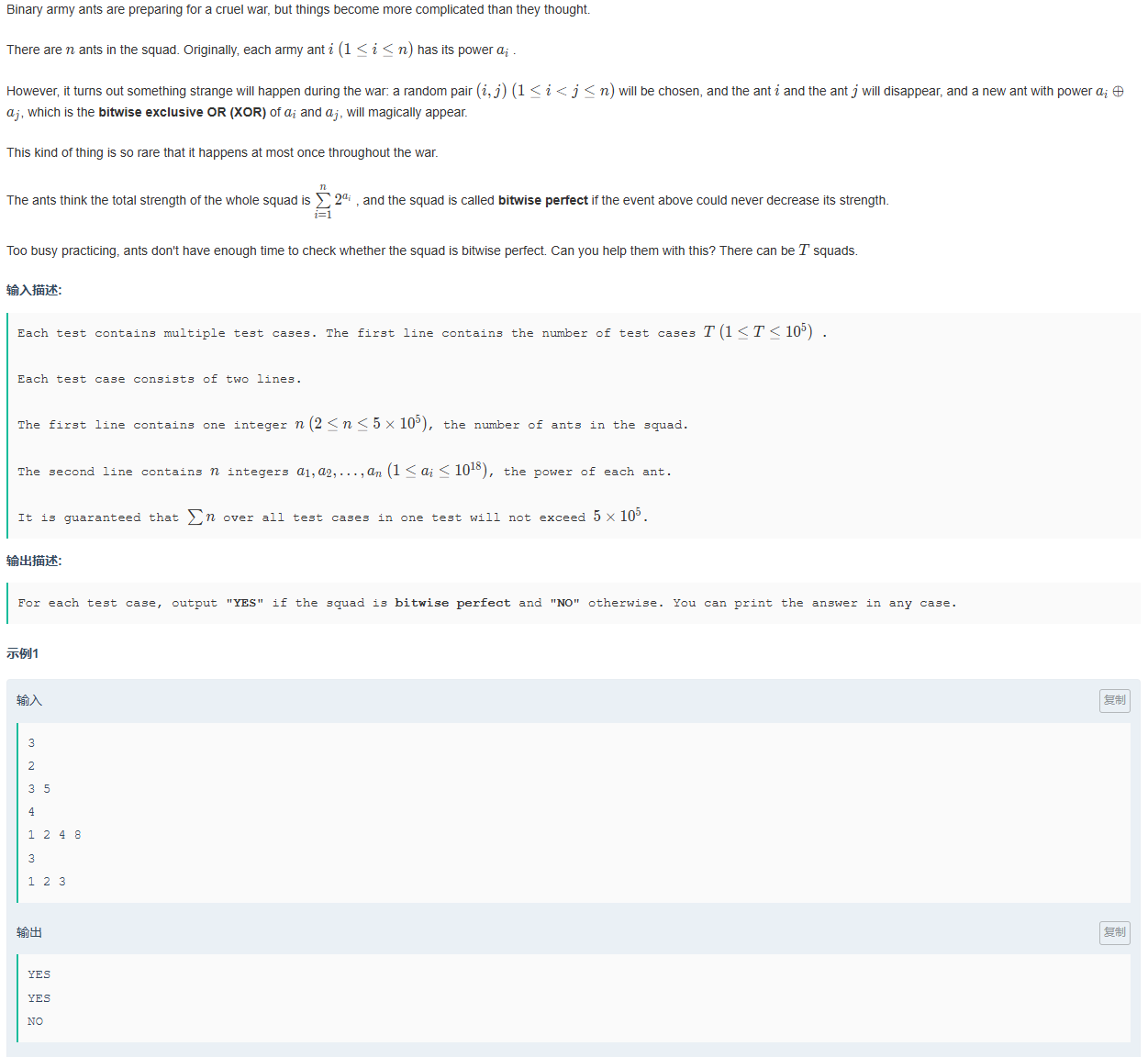
给定一个数组,如果在该数组中找到了两个数异或之后小于该两个数字,则输出NO,否则输出YES。
思路:
题目要求找到异或之后的数字变原先的两个都大,故我们直接去枚举每个数字的最高位置,最高位置和下一位数字&不能为1,否则两者异或必将减小。
维护最高位置下的数字,从到尾扫一遍数组即可。还有一个坑点其实就是要从小到大对数组进行维护,因为小数可以涵盖大数,而大数难以涵盖小数。
#include<bits/stdc++.h>
using namespace std;
#define int long long
void solve(){int n;cin>>n;vector<int>a(n);for(int &x:a){cin>>x;}sort(a.begin(),a.end());int sum=0;bool ok=0;for(auto it:a){if(sum&it){//判断最高位维护的数字下是否和下一个数字之间有重复的地方ok=1;break;}int zuida=63-__builtin_clzll(it);//二进制小从左到右第一个1的位置sum|=(1ll<<zuida);//维护最高位数字}if(ok)cout<<"NO"<<endl;else cout<<"YES"<<endl;
}
signed main(){int T;cin>>T;while(T--)solve();
}
题目意思:
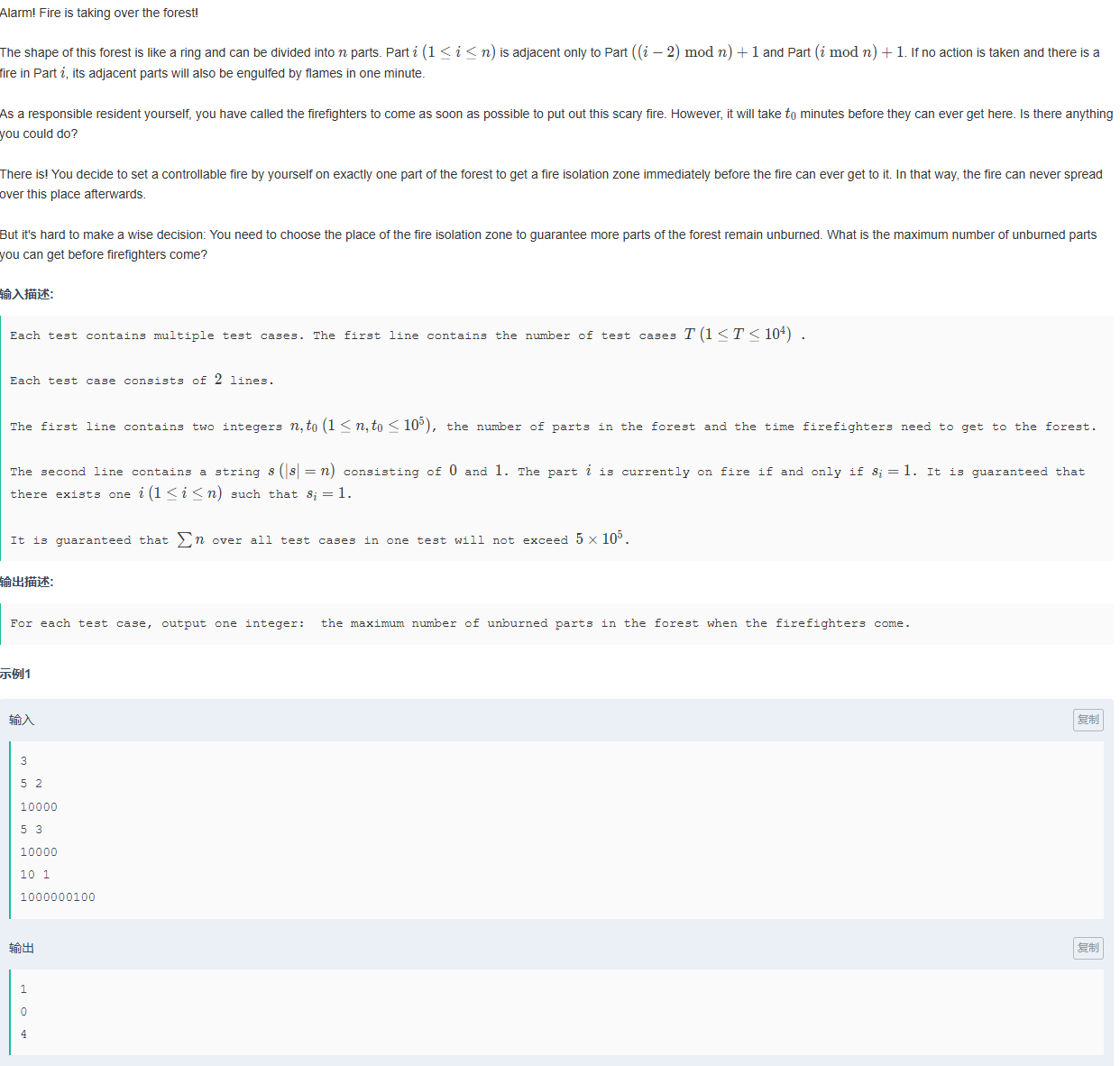
定义01串,1为起火位置,每分钟会沿着左右蔓延,0为未起火位置,消防员会在t0时刻之后到。
如果让你画出一个防火带,在t0分钟你可以救下最多多少未起火位置。
思路:
01串前后构成一个环,考虑每段0,在t0分钟之后,先求出不画出防火带的情况下能救下多少没有起火的位置。
在根据每段0求出最大救下没有起火位置的个数,最后两者相加即可。
此时我们要对t0和0串长度g进行考虑
当 2*t0>=g的时候,此时我们如果不设置防火带的情况下,所有0肯定会变成1,那么此时的最优解法就是在边界放置防火带,此时我们极限救下的0串的个数就是g-1-t0
当g>2*t0的时候,此时我们也只用在边界防止防火带即可,不过这次我们要统计的是救下的0串,即没救之前被烧成1。此时极限救下0串的个数是t0-1
最后我们对两个求个min即可。
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline void solve(){int n,t0;string s;cin>>n>>t0>>s;vector<int>p;for(int i=0;i<s.size();i++){if(s[i]=='1')p.push_back(i+1);}if(p.size()==n){//都是1的情况cout<<0<<endl;return ;}int sum=0;vector<int>ga;for(int i=0;i<p.size()-1;i++){ga.push_back(p[i+1]-p[i]-1);//0串的长度}ga.push_back(n-1-p[p.size()-1]+p[0]);sort(ga.begin(),ga.end());for(auto it:ga){sum+=max(0ll,it-2*t0);//不设置防火带情况下能保住多少0}int jia=0;for(auto it:ga){int d=min(it-t0-1,t0-1);//设置之后能保住多少if(d>0)jia=max(jia,d);}cout<<jia+sum<<endl;
}
signed main(){int t;cin>>t;while(t--)solve();
}
题目意思:
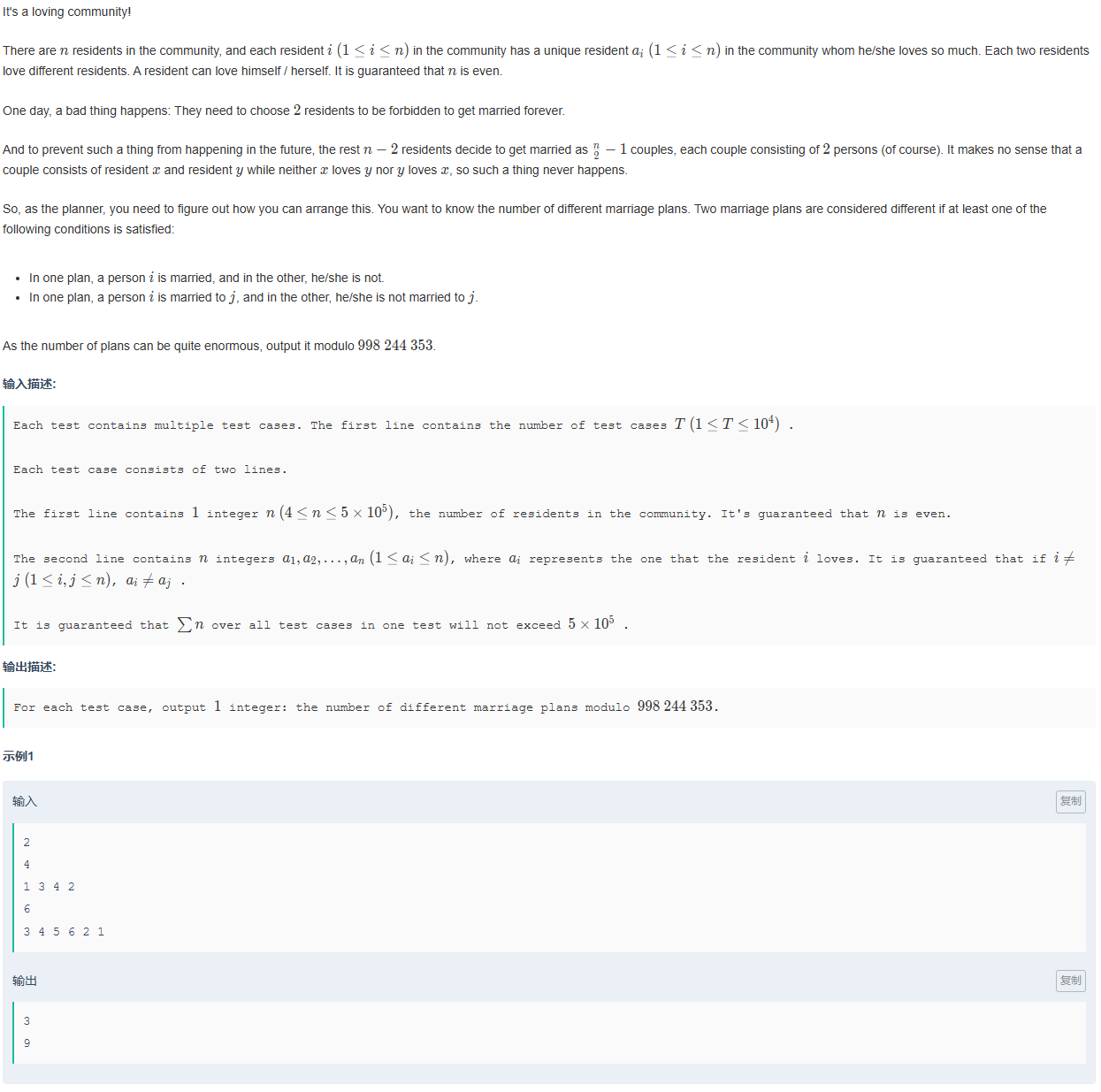
在一个社区中有 n 位居民(n 为偶数),每位居民 i 有一个唯一喜欢的居民 ai(可能喜欢自己)。题目保证:
每个居民的喜欢对象是唯一的(即 ai 互不相同)
n 是偶数
需要禁止 2 位居民结婚(即从 n 人中移除 2 人)。
剩下的 n−2 位居民需要组成 2n−1 对夫妻(即完全配对)。
配对的规则是:夫妻中的两人必须互相喜欢(即 x 和 y 配对当且仅当 ax=y 且 ay=x)
思路:
我们不妨按照题目要求画出流程图,不难发现,实质上就是让我们分析环之间的关系(若干个偶数环或者若干个偶数环+两个奇数环)
则我们先对奇数环进行分析,发现奇数环的个数必定是2或者0,在2的情况下,我们只能对奇数环进行操作,由于没有确定男女,故奇数环的贡献是两者长度之积。最后在乘上偶数环的贡献即可,
此时偶数环由于不能删去数字,贡献只能是方向去向问题,长度大于2的贡献为2,长度=2的贡献为1,最后对全部偶数环整个相乘即可。
偶数环删去的贡献,当偶数环的长度是2的时候,此时我们不能删去,故此时的贡献是1
当偶数环的长度大于2的时候,我们删去两个,一定是一男一女。男生的数量L/2女生的数量L/2,那么此时的贡献就是两者之积。
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int op=998244353;
int kuai(int a,int b){int sum=1;while(b){if(b&1)sum=(sum*a)%op;a=(a*a)%op;b>>=1;}return sum;
}
const int div2=kuai(2,op-2);
void solve(){int n;cin>>n;vector<int>a(n+1);for(int i=1;i<=n;i++)cin>>a[i];vector<bool>vis(n+1,0);vector<int>odd,even;for(int i=1;i<=n;i++){//找环if(!vis[i]){int u=i,len=0;do{vis[u]=1;len++;u=a[u];}while(u!=i);if(len&1)odd.push_back(len);else even.push_back(len);}}int k=odd.size();if(k!=0&&k!=2){//奇环的个数必定是0或者2cout<<0<<endl;return ;}int sum=1;int cnt=0;for(auto to:even){if(to!=2)sum=(sum*2)%op;//旋转的偶数环贡献int z=to/2;int L=(z*z)%op;if(to!=2)cnt=(cnt+L*div2)%op;//这里的逆元是旋转对称性导致某些配对方式被重复计算else cnt=(cnt+1)%op;}if(k==0){//没有奇数环的情况下cout<<(cnt%op*sum%op)%op<<endl;}else cout<<(((odd[1]%op*odd[0]%op)%op)*sum)%op<<endl;//奇偶环
}
signed main(){int t;cin>>t;while(t--)solve();
}