[每日随题14] 递推 - 滑动窗口 - 数学

整体概述

• 难度：900 $\to$ 1400 $\to$ 2000

---

P10250 [GESP样题 六级] 下楼梯

• 标签：递推

• 前置知识：无

• 难度：橙 900

题目描述：

输入格式：

输出格式：

样例输入：

4

10

样例输出：

7

274

解题思路：

• 简单的水题，$d{p}_i=d{p}_{i-1}+d{p}_{i-2}+d{p}_{i-3}$，$d{p}_1=1$，$d{p}_2=2$，$d{p}_3=4$。

• 从小到大推一遍即可，复杂度 $O(n)$。

完整代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 65;
int dp[N];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);dp[1] = 1,dp[2] = 2,dp[3] = 4;int n; cin >> n;for(int i=4;i<=n;i++) dp[i] = dp[i-1]+dp[i-2]+dp[i-3];cout << dp[n];return 0;
}

---

P8551 Bassline

• 标签：滑动窗口

• 前置知识：STL-priority_queue

• 难度：黄 1500

题目描述：

输入格式：

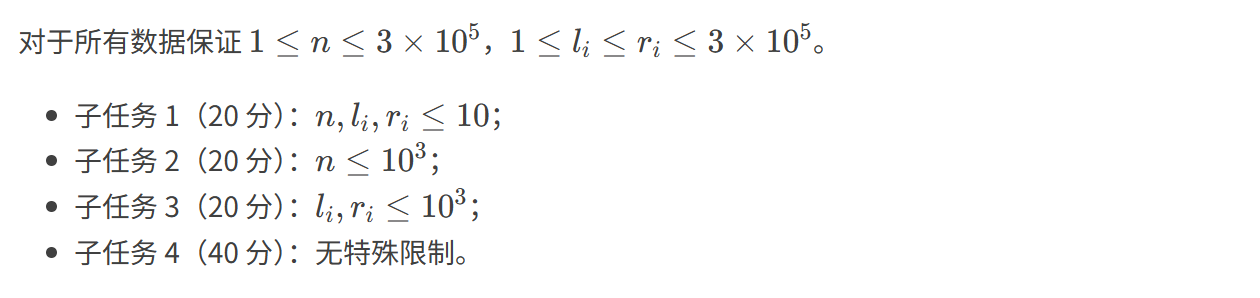
输出格式：

样例输入：

4
1 3
4 7
5 9
7 10

样例输出：

2

解题思路：

• 题目要求找到某个区间 $[x,y]$ 满足对于所有区间，要么包含 $[x,y]$ 要么与 $[x,y]$ 不相交，此时贡献为 $包含[x,y]的区间个数\ast (y-x)$。

• 我们发现 $l，r$ 的范围很小，那么我们可以暴力枚举 $x$，求对于每个 $x$ 的最大 $y$ 是多少。

• 那么会限制 $y$ 的只有左端点包含了 $x$ 的区间的右端点，以及左端点小于 $y$ 的区间左端点。那么我们先将区间按 $l$ 从小到大排序，在枚举 $x$ 的过程中将大于 $i$ 的区间的右端点丢进优先队列中，对于前者可以快速从优先队列找到最小的 $r$，对于后者可以在排过序的区间左端点里二分，直接得到大于 $i$ 的最小区间左端点。

• 至此问题解决，总复杂度 $O(n\cdot lo{g}_{2}n)$。

完整代码

#include<bits/stdc++.h>
#define int long long
#define Size(x) ((int)(x).size())
using namespace std;
const int N = 3e5+5, INF = 0x3f3f3f3f;
int n,m; bool out[N];
struct Node{int l,r;}a[N];
priority_queue<int,vector<int>,greater<int>> qu;
inline int up_min(int x){int l = 1,r = n,mid;while(l<=r){mid = (l+r)>>1;if(a[mid].l > x) r = mid-1;else l = mid+1;}return l == n+1 ? INF : a[l].l;
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin >> n;for(int i=1;i<=n;i++) cin >> a[i].l >> a[i].r, m = max(m,a[i].r);sort(a+1,a+n+1,[&](Node x,Node y){return x.l < y.l;});int p = 1, res = 0;for(int i=1;i<=m;i++){while(p<=n && a[p].l == i) qu.push(a[p++].r);while(!qu.empty() && qu.top() < i) qu.pop();if(!qu.empty()){int r = min(up_min(i)-1,qu.top());res = max(res,Size(qu)*(r-i));}  }cout << res;return 0;
}

---

P2424 约数和

• 标签：数学

• 前置知识：无

• 难度：蓝 2000

题目描述：

输入格式：

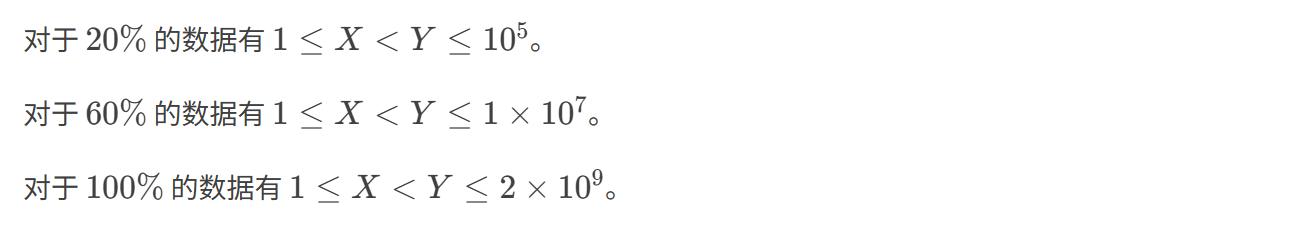
输出格式：

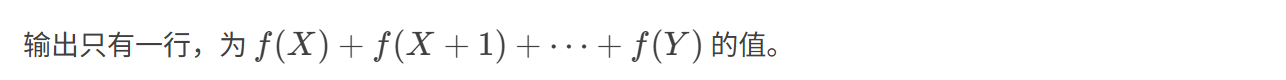
样例输入：

2 4

123 321

样例输出：

14

72543

解题思路：

• 首先我们考虑如何快速求 ${\sum }_{i=1}^{n}f(n)$，考虑贡献法。

• 我们可以枚举 $[1,n]$ 的每个数字，判断有其有多少个倍数，即该数字作为约数贡献了多少次，那么 ${\sum }_{i=1}^{n}f(n)={\sum }_{i=1}^n\lfloor \frac{n}{i}\rfloor \ast i$。

• 可是这样复杂度为 $O(n)$，而 $n$ 高达 $2\times 10^9$，还需要优化。

• 我们随便选个 $n=12$ 来观察序列 $\lfloor \frac{n}{i}\rfloor$ 有什么性质：$12,6,4,3,2,2,1,1,1,1,1,1$。

  发现其中有明显的连续重复项，考虑这是如何产生的，重复项的区间 $[l,r]$ 被如何确定。

• 序列 $\lfloor \frac{n}{l}\rfloor$ 代表着约数 $l$ 的出现次数，那么使得 $\lfloor \frac{n}{x}\rfloor =\lfloor \frac{n}{l}\rfloor$ 的最大 $x$ 即为 $\lfloor \frac{n}{\lfloor \frac{n}{l}\rfloor }\rfloor$，所以我们可以加快枚举约数的过程，将所有约数个数相同的约数的贡献一并计算。

• 复杂度与 $O(\sqrt{n})$ 同阶。

完整代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
inline int sum(int n){int res = 0,l,r;for(l=1;l<=n;l=r+1){	// l 为约数int cnt = n/l;		// cnt 为约数 l 出现的个数r = n/cnt;		// r 表示最大的 (约数个数为cnt) 的约数res += cnt * ((l+r)*(r-l+1)/2);	// 此时 [l,r] 范围内的约束均有 cnt 个,等差数列求和}return res;
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);int x,y; cin >> x >> y;cout << sum(y) - sum(x-1);return 0;
}

---