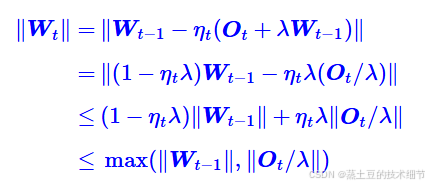Muon小记

苏神博客：https://spaces.ac.cn/archives/10739
muon：https://blog.csdn.net/kebijuelun/article/details/146072294
kimi的muon：https://papers.cool/arxiv/2502.16982

矩阵白化

考研知识，就是主成分分析。一个矩阵就是一个n维空间的基，把它变成基正交，且单位化，就是白化。方法是计算矩阵的协方差矩阵，然后找一个把协方差矩阵变成单位矩阵的白化矩阵。

Newton-Schulz 牛顿施瓦茨方法

这就是找白化矩阵的方法，是一种迭代找解的方法，因此是一个近似解。

Muon

一个优化器好不好，主要看两点：1.你别把我的模型训崩了，即要稳。2.你别磨磨唧唧的半天训不好，即要快。这两个肯定是稳占主要，然后才考虑快。
训练是对参数矩阵W的作用，令W的变化是ΔW。稳和快，完全体现在ΔW的改变上。

既然稳是第一步，那就把稳写到s.t.里。ρ是一个函数，鬼知道是什么形式，总之肯定和ΔW有关，且知道ΔW越大越不稳(规范点说是它的范数越大越不稳)，所以给他限制到η里。为了方便，干脆让ρ是一个非负的函数，这也正好契合用范数描述矩阵性质这个好用的数学工具。注意，范数>=0。

然后是快，快是指loss往最低点走。假设W对loss的梯度为G，G描述的是W参数空间上该W的周围对loss影响的大小。计算GTΔW，是在计算：假如我W改变了ΔW，那么在各个梯度方向上，对最终结果的变化有多少，这和Δy=kΔx是一个道理，k是梯度。
Tr()，即计算trace，是在计算矩阵特征值之和，放在GTΔW上，就是在算各个方向上的影响loss的程度之和。我们是该专注一个方向猛猛优化loss，还是百花齐放，每个方向都优化一下呢？当然是前者，后者很容易在拉扯中把模型给训崩了，专注于一个n维的方向是最理想的。所以这里要求的是argmin，要让W的变化ΔW在W所处的梯度矩阵G上有一个专一的优化方向，专一等于快。

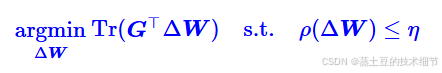
优化公式有了，就差不知道ρ函数是什么了。
前面说了，我们设计的时候已经知道用范数做度量是最方便的了，所以就在范数里选吧。哪个范数能看出一个矩阵“稳不稳”？我不知道，我理解不上去，但是我知道，F范数是特征值的总和，谱范数是最大的特征值，貌似F有点暴力，它一总和，那些微小改变的方向也开始以极大比重影响起对“稳”的判断了，或许那些方向动一点点也没关系
F范数就是SGD为了让模型稳使用的范数，它要求每次更新的ΔW的F范数较小。所以谱范数优于F范数。

那么最后的优化目标就是这个了：

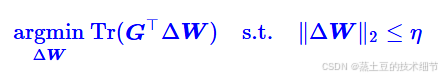
G属于已知量，η是超参，求ΔW。解完是这样：

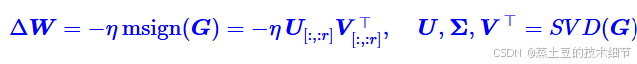
实际更新规则如下：

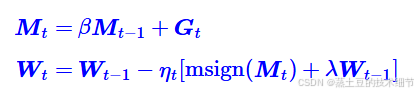
M是动量，Muon中的Mu，加上这个属于是标准操作了。
msign是这样的操作：先把M给SVD了，即UΣV=M，然后msign(M)=UV，but只计算那些有秩的维度。
如果λ=0，这是原版Muon的更新公式。然而实操中发现weight decay现象，导致Muon一开始训练快，后面被Adam追上。所以加上这一项。

苏神的分析认为，不扣掉一部分原本的W，会让更新后的W的范数无界，而先扣掉一点就有界了：