hot100——第八周
目录
实现 Trie (前缀树)
全排列
子集
字符串相乘
电话号码的字母组合
组合总和
括号生成
单词搜索
分割回文串
N 皇后
搜索插入位置
在排序数组中查找元素的第一个和最后一个位置
搜索二维矩阵
搜索旋转排序数组
寻找旋转排序数组中的最小值
实现 Trie (前缀树)
解法1:set
使用unordered_set容器进行储存遍历
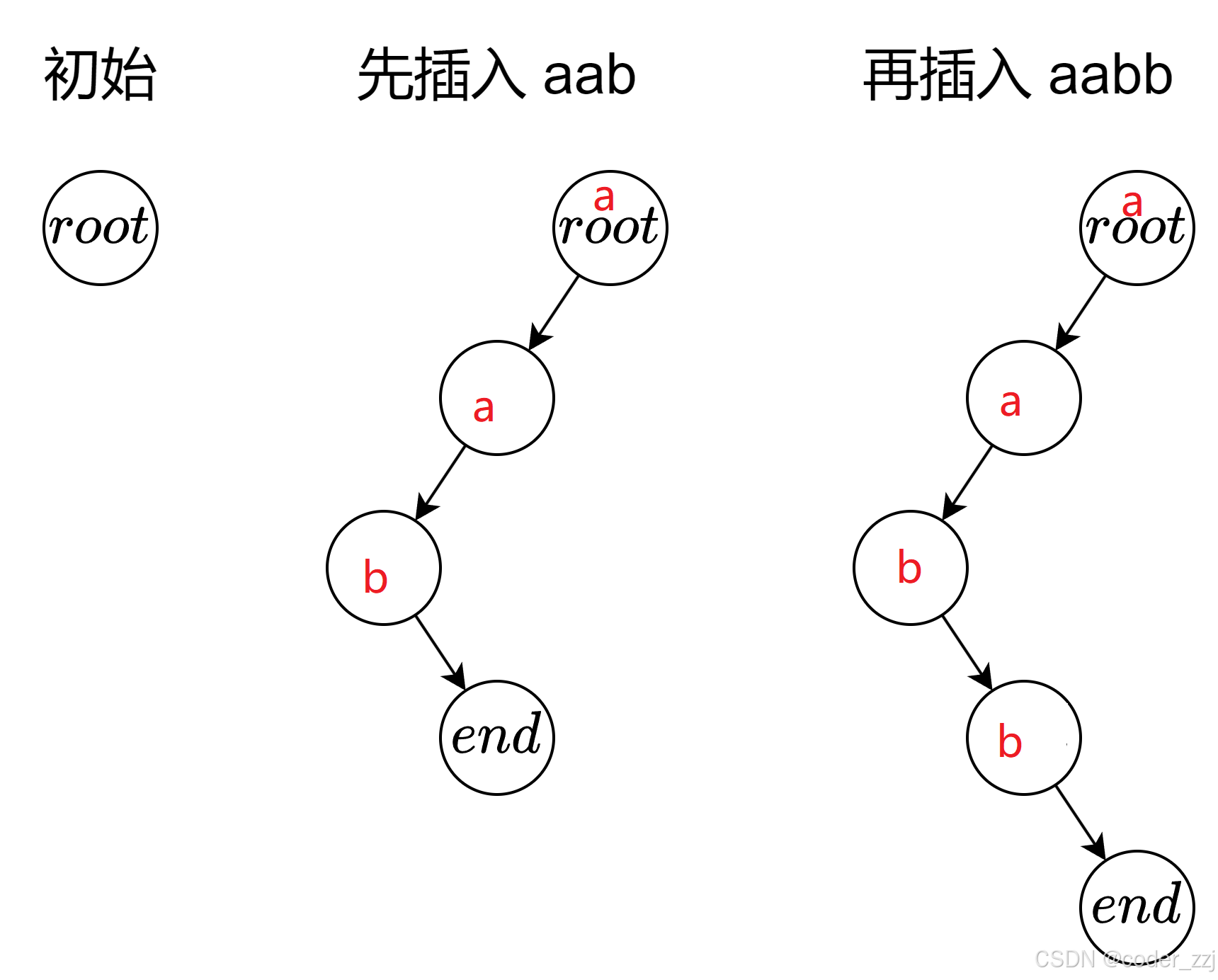
解法2:多叉树
根据题目构建出一个26叉树,用数组来储存每个节点
class Trie
// {
// public:
// unordered_set<string> hash;
// Trie()
// {
// }// void insert(string word)
// {
// hash.insert(word);
// }// bool search(string word)
// {
// return hash.contains(word);
// }// bool startsWith(string prefix)
// {
// for (auto &e : hash)
// {
// int pos = 0, i = 0;
// while (pos < e.size() && i < prefix.size() && e[pos] == prefix[i])
// {
// pos++;
// i++;
// }
// if (pos <= e.size() && i == prefix.size())
// return true;
// }
// return false;
// }
// };class Trie
{
public:typedef struct Node{struct Node *NodeList[26] = {nullptr};bool end = false;} Node;Trie(){_root = new Node;}void insert(string word){Node *cur = _root;for (int i = 0; i < word.size(); i++){int pos = word[i] - 'a';if (cur->NodeList[pos] == nullptr){cur->NodeList[pos] = new Node;}cur = cur->NodeList[pos];}cur->end = true; // 最后一个字符的下一个节点进行标记}// 0->找不到 1->精确匹配 2->前缀匹配int find(const string &word){Node *cur = _root;for (int i = 0; i < word.size(); i++){int pos = word[i] - 'a';if (cur->NodeList[pos] == nullptr)return 0;cur = cur->NodeList[pos];}return cur->end == true ? 1 : 2;}bool search(string word){return find(word) == 1;}bool startsWith(string prefix){return find(prefix) != 0;}private:Node *_root;
};全排列
解法:dfs
回溯模板题
class Solution
{
public:vector<vector<int>> ret;vector<int> path;bool vis[7] = {false}; // 当前位置进行标记void dfs(vector<int> &nums){if (path.size() == nums.size()){ret.push_back(path);return;}for (int i = 0; i < nums.size(); i++){if (!vis[i]){vis[i] = true;path.push_back(nums[i]);dfs(nums);path.pop_back();vis[i] = false;}}}vector<vector<int>> permute(vector<int> &nums){dfs(nums);return ret;}
};子集
解法1:dfs
从当前位置往后枚举每个数,每次递归枚举之前收集结果
解法2:位运算
class Solution {
public:vector< vector<int> > ret;vector<int> path;void dfs(vector<int>& nums,int pos){if(path.size() > nums.size()) return;ret.emplace_back(path);for(int i= pos;i < nums.size();i++){path.push_back(nums[i]);dfs(nums,i + 1);path.pop_back();}}vector<vector<int>> subsets(vector<int>& nums) {dfs(nums,0);return ret;}
};字符串相乘
解法1
先把两个字符串翻转;
遍历其中一个数的每一位于另一个数相乘(如果是十位,百位要先补0),每次得到的结果进行字符串相加...
最终结果的string要进行翻转才能得到最终的结果
解法2
先把两个字符串翻转;
创建一个数组用来保存每一位与每一位计算的结果;
之后处理数组时往后进位,使用string保存每一位的结果;
最后string要进行翻转才能得到最终结果
class Solution
{
public:string multiply(string num1, string num2){int m = num1.size(), n = num2.size();vector<int> tmp(m + n - 1, 0);for (int i = 0; i < m; i++){for (int j = 0; j < n; j++){tmp[i + j] += (num1[i] - '0') * (num2[j] - '0');}}string ret;// tmp的数据写成string类型int flag = 0;for (int i = m + n - 2; i >= 0; i--){int sum = tmp[i] + flag;ret += sum % 10 + '0';flag = sum / 10;cout << ret << endl;}if (flag != 0)ret += flag + '0';reverse(ret.begin(), ret.end());return ret;}
};电话号码的字母组合
解法:dfs
先用一个数组对储存数字映射的字符串(下标访问);
画决策树设计dfs
class Solution
{
public:string arr[10] = {"0", "0", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};vector<string> ret;string path;void dfs(string &s, int pos){if (pos == s.size()){ret.push_back(path);return;}for (auto &e : arr[s[pos] - '0']){path += e;dfs(s, pos + 1);path.pop_back();}}vector<string> letterCombinations(string digits){if (digits.size() == 0)return ret;dfs(digits, 0);return ret;}
};组合总和
解法:dfs
画出决策树,每次从当前位置进行往后枚举(递归):如果当前位置越界或者值大于等于target就要判断是否是答案后进行收集
class Solution
{
public:vector<vector<int>> ret;vector<int> path;int sum = 0;void dfs(vector<int> &candidates, int target, int pos){if (sum >= target || pos == candidates.size()){if (sum == target)ret.push_back(path);return;}for (int i = pos; i < candidates.size(); i++){path.push_back(candidates[i]);sum += candidates[i];dfs(candidates, target, i);sum -= candidates[i];path.pop_back();}}vector<vector<int>> combinationSum(vector<int> &candidates, int target){dfs(candidates, target, 0);return ret;}
};括号生成
思路1:选不不选
递归时有两种选:要么选择左括号,要么选择右括号:前提是 当前收集到的左括号 >= 右括号的数量
思路2:枚举
枚举右括号的数量,之后添加一个左括号,递归时传入两个参数:第一个参数递归后填写的位置;第二个参数是递归后枚举符合范围的右括号的数量
class Solution
{
public:vector<string> ret;string path;int left = 0, right = 0, sum;void dfs(){// left个数不符合要求或者左括号数量小于右括号的数量都是不符合题意if (left > sum / 2 || left < right)return;if (left + right == sum){ret.push_back(path);return;}// 选左left++;path += '(';dfs();left--;path.pop_back();// 选右right++;path += ')';dfs();right--;path.pop_back();}vector<string> generateParenthesis(int n){sum = 2 * n;dfs();return ret;}
};class Solution
{
public:vector<string> ret;vector<int> left_index;vector<string> generateParenthesis(int n){auto dfs = [&](this auto &&dfs, int pos, int CurrentRightNum){if (left_index.size() == n){string s(2 * n, ')');for (auto &i : left_index)s[i] = '(';ret.push_back(s);return;}// 枚举右括号个数for (int num = 0; num <= CurrentRightNum; num++){// 根据右括号个数确定放置左括号的坐标left_index.push_back(pos + num);dfs(pos + num + 1, CurrentRightNum - num + 1); // 下次递归的位置与右括号的个数left_index.pop_back();}};dfs(0, 0);return ret;}
};单词搜索
解法:dfs
枚举每个位置:如果与第一个单词的字符相同就继续上下左右四个方向进行递归
class Solution
{
public:string path;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};bool vis[7][7] = {false};bool exist(vector<vector<char>> &board, string word){int n = board.size(), m = board[0].size();auto dfs = [&](this auto &&dfs, int i, int j, int pos){if (pos == word.size())return true;for (int k = 0; k < 4; k++){int x = dx[k] + i, y = dy[k] + j;if (x >= 0 && x < n && y >= 0 && y < m && !vis[x][y] && board[x][y] == word[pos]){vis[x][y] = true;if (dfs(x, y, pos + 1))return true;vis[x][y] = false;}}return false;};for (int i = 0; i < board.size(); i++){for (int j = 0; j < board[0].size(); j++){if (board[i][j] == word[0]){vis[i][j] = true;if (dfs(i, j, 1))return true;vis[i][j] = false;}}}return false;}
};分割回文串
解法:dfs
分与不分:如果当前位置要进行分割,就先判断分割后的字符串是否是回文,不是自己向上返回,是就从下一个位置递归来分割字符串;如果不分就继续找下一个分割位置(最后一个位置也就是字符串结尾,无论如何都是要进行分割的(边界))
// 分割字符串
class Solution
{
public:vector<vector<string>> ret;vector<string> path;bool IsTrue(string &s, int begin, int end){while (begin < end){if (s[begin++] != s[end--])return false;}return true;}vector<vector<string>> partition(string s){int n = s.size();// begin:字符串的起始位置 pos:当前位置的前面需不需要分割auto dfs = [&](this auto &&dfs, int begin, int pos){if (pos == n){ret.push_back(path);return;}if (pos < n - 1)// n== n-1一定要分{// 不分dfs(begin, pos + 1);}// 分if (IsTrue(s, begin, pos)){path.push_back(s.substr(begin, pos - begin + 1));dfs(pos + 1, pos + 1);path.pop_back();}};dfs(0, 0);return ret;}
};N 皇后
解法:dfs
难点:怎么处理正斜线与副斜线有无皇后?
行列坐标相加后相同证明在同一正斜线
行列坐标相减后相同证明在同一副斜线
(多个几个空间不然数组会越界)
class Solution
{
public:bool row[10], col[10], vis1[20], vis2[20];vector<string> path;vector<vector<string>> ret;vector<vector<string>> solveNQueens(int n){string s;s.resize(n, '.');path.resize(n, s);auto dfs = [&](this auto &&dfs, int rows){if (rows == n){ret.push_back(path);return;}for (int j = 0; j < n; j++){if (path[rows][j] == '.' && !row[rows] && !col[j] && !vis1[rows + j] && !vis2[rows - j + n]){row[rows] = col[j] = vis1[rows + j] = vis2[rows - j + n] = true;path[rows][j] = 'Q';dfs(rows + 1);path[rows][j] = '.';row[rows] = col[j] = vis1[rows + j] = vis2[rows - j + n] = false;}}};dfs(0);return ret;}
};搜索插入位置
解法:二分
使用朴素二分查找模版
class Solution
{
public:int searchInsert(vector<int> &nums, int target){int left = 0, right = nums.size() - 1;while (left <= right){if (nums[left] < target)left++;else if (nums[right] > target)right--;elsebreak;}return left;}
};在排序数组中查找元素的第一个和最后一个位置
解法:二分
使用非朴素二分的两个模板进行求解
class Solution
{
public:vector<int> searchRange(vector<int> &nums, int target){int n = nums.size();if (n == 0)return {-1, -1}; // 边界判断int left = 0, right = n - 1;// 求左端点while (left < right){int mid = (left + right) / 2;if (nums[mid] < target)left = mid + 1;elseright = mid;}if (nums[left] != target)return {-1, -1}; // 没找到target直接返回int tmp = left;// 求右端点left = 0, right = n - 1;while (left < right){int mid = (left + right + 1) / 2;if (nums[mid] > target)right = mid - 1;elseleft = mid;}return {tmp, left};}
};搜索二维矩阵
解法1:二分
将二维矩阵转成递增的数组后进行二分
解法2:排查
从第一行的最后一个数开始排查:(坐标在合法的范围内)
如果当前值小于目标值则说明当前行都不符合往下一行查询;
如果当前值大于目标值则说明值可能在当前行,往左走;
等于就直接返回true
循环出来后没返回说明找不到返回false
class Solution
{
public:bool searchMatrix(vector<vector<int>> &matrix, int target){int n = matrix.size(), m = matrix[0].size();int i = 0, j = m - 1;while (i < n && j >= 0){if (matrix[i][j] < target)i++;else if (matrix[i][j] > target)j--;elsereturn true;}return false;}
};搜索旋转排序数组
解法1:两次二分
找排序数组的终点值分为两个数组进行两次二分找目标值target
解法2:二分
按照 target 在 x(中间值)的左边进行分类讨论:(如果等于就返回x下标,剩下的就是target在x右边的情况)
- 当 target 和 x 都在左半段排序数组时,两者都要大于数组最后一个值且target小于x(即使数组只有一段它也是降序的,可以使用来判断)
- x在右半段排序数组中,此时target可以在左半段,也可以在右半段
class Solution
{
public:int search(vector<int> &nums, int target){int left = 0, right = nums.size() - 1;while (left <= right){int mid = (left + right) / 2;if (nums[mid] == target)return mid;else if ((target > nums[right] && target < nums[mid]) ||(nums[mid] < nums[right] && (target < nums[mid] || target > nums[right]))){right = mid - 1;}elseleft = mid + 1;}return -1;// 两次二分// int i=0,n=nums.size();// while(i+1<n && nums[i]<nums[i+1]) i++;// int left=0,right=i;// while(left<=right)// {// int mid=(left+right)/2;// if(nums[mid]<target) left=mid+1;// else if(nums[mid]>target) right=mid-1;// else return mid;// }// left=i+1,right=n-1;// while(left<=right)// {// int mid=(left+right)/2;// if(nums[mid]<target) left=mid+1;// else if(nums[mid]>target) right=mid-1;// else return mid;// }// return -1;}
};寻找旋转排序数组中的最小值
解法:二分
使用非朴素二分模板,中间位置的值与当前区间的最后一个位置的值进行比较:
中间值大于最后一个值说明:中间值在左半段,最小值在右半段;
剩下的情况说明:中间值可能是最小值,也可能在中间值的左边(但都一定在右半段)
class Solution
{
public:int findMin(vector<int> &nums){int left = 0, right = nums.size() - 1;while (left < right){int mid = (left + right) / 2;if (nums[mid] > nums[right])left = mid + 1;elseright = mid;}return nums[left];}
};以上便是全部内容,有问题欢迎在评论区指正,更新观看!
