【论文阅读笔记】RF-Diffusion: Radio Signal Generation via Time-Frequency Diffusion

论文信息

题目	RF-Diffusion: Radio Signal Generation via Time-Frequency Diffusion
作者	Guoxuan Chi, Zheng Yang, Chenshu Wu, Jingao Xu, Yuchong Gao, Yunhao Liu, Tony Xiao Han
单位	清华大学，香港大学，北京邮电大学，华为技术有限公司
发表	2024 MobiCom

论文翻译

Abstract — 随着AIGC在计算机视觉和自然语言处理领域的蓬勃发展，其在无线领域的潜力近年来也开始显现。然而，现有的面向射频的生成式解决方案由于有限的表征能力，并不适合生成高质量的时序射频数据。在这项工作中，受到扩散模型在计算机视觉和自然语言处理领域取得的卓越成就的启发，我们将其应用于射频领域，并提出了 RF-Diffusion。为了适应射频信号的独特特性，我们首先引入了一种新颖的时频扩散理论来增强原始扩散模型，使其能够挖掘射频信号在时间、频率和复值域中的信息。在此基础上，我们提出了一个分层扩散 Transformer，通过精心的设计（包括网络架构、功能模块和复值算子）将该理论转化为一个实用的生成式 DNN，使 RF-Diffusion 成为一个通用的解决方案，可以生成多样、高质量和时序的射频数据。与三种流行的生成模型的性能比较表明，RF-Diffusion 在合成 Wi-Fi 和 FMCW 信号方面具有卓越的性能。我们还展示了 RF-Diffusion 在提升 Wi-Fi 传感系统性能以及在 5G 网络中执行信道估计方面的多功能性。
Index Terms — 射频信号, 生成模型, 时频扩散, 无线感知, 信道估计。

---

1 Introduction

人工智能生成内容（Artificial Intelligence Generated Content，AIGC）已在工业和学术前沿引发了革命性的影响，催生了一系列基于深度神经网络（Deep Neural Networks，DNN）的尖端产品。卓越的例子包括用于图像创建的 Stable Diffusion [54]、Midjourney [43]、DALL-E [51]，以及用于文本生成的ChatGPT [46]。

如今，AIGC 正逐渐叩开射频（Radio-frequency，RF）领域的大门。目前的实践初步证明了其在数据增强 [53]、信号去噪 [7] 和时间序列预测 [22] 方面提升无线系统的潜力。在诸如设备定位 [76]、人体运动感知 [72] 和信道估计 [38] 等下游任务中，这种进步不仅提高了系统性能，还减少了应用层 DNN 训练中繁琐的 ground truth 标注成本。

现有的射频数据生成模型大致可以分为两大类：

• 基于环境建模的生成模型。该方法利用激光雷达点云或视频镜头构建环境的详细 3D 模型。随后，它采用物理模型（如光线追踪 [42]）模拟射频信号与周围环境的相互作用，最终有助于预测接收机可能捕获的信号。然而，该方法的一个显著局限在于其对目标材料和属性如何影响射频信号传播的考虑不足。此外，获取与射频信号波长（例如 1-10 毫米）兼容的 3D 模型仍面临挑战，并将显著增加系统开销。尽管近期研究利用神经辐射场对射频复杂环境进行隐式建模以估算信号传播 [76]，但该方法要求接收机（Rx）保持静止，这使得生成无线通信系统或人体动作识别等任务所需的关键时间序列数据变得复杂。
• 数据驱动的概率生成模型。目前的创新利用生成对抗网络 (Generative Adversarial Network，GAN) 和变分自编码器 (Variational Autoencoder，VAE) 等模型来扩充射频数据集 [21]。本质上，这些模型学习训练数据中的分布，然后生成遵循此分布的新射频数据。然而，由于其受限的表示能力，这些模型主要侧重于扩展特征级分布，并且难以精确生成原始射频信号 [72]。此外，它们中的大多数是为具有专用损失函数和 DNN 架构的特定任务而设计的，从而限制了它们的通用性。另一方面，由于生成器和判别器之间的拉锯战，GAN 的训练是出了名的变化无常 [69]。备注。尽管具有启发性，但仍然缺乏一种通用的生成模型来生成准确且时序的原始射频信号，以适用于各种下游应用。

近来，扩散模型已成为视觉人工智能生成内容领域一颗耀眼的明星，为各种创新型深度神经网络奠定了基础，这些神经网络应用于一系列突出的图像/视频应用，如 Stable Diffusion、Midjourny 和 DALL-E。与上述生成模型相比，其独特的噪声添加（即加噪）和去除（即去噪）的迭代过程能够精确捕获复杂的原始数据分布 [70]。此外，它的训练过程简单明了，避免了诸如模式崩溃或收敛困难等典型问题，因为它不需要处理相互竞争的部分，也不需要精细的微调 [13]。

这些引人注目的优势促使我们采用 扩散模型 来合成射频数据。然而，将现有的扩散模型 [25] 迁移到射频领域面临着严峻的挑战，这些挑战源于射频信号超越图像的独特特性，总结如下。

（i）时间序列。与静态快照不同，射频信号可以捕捉目标运动和环境/信道随时间变化的动态细节。为单图像生成设计的扩散模型难以合成射频信号序列。
（ii）频域 。重要的射频细节（例如，多普勒频移、线性调频）嵌入在频域中。虽然最近的视频扩散模型可以创建时间序列，但它们主要关注空间域（例如，像素亮度），从而忽略了频域中的丰富信息。
（iii）数域 。射频数据是复数值的，既有幅度读数也有相位读数。虽然现有的扩散模型只关注幅度（例如，光强度），但相位数据由于其在无线系统中的关键作用而不可忽略。总之，虽然扩散模型具有很大的潜力，但有必要升级当前的模型，以适应射频信号的独特特性，并挖掘时域、频域和复数值域中的潜在信息。

我们的工作。我们提出了 RF-Diffusion，这是第一个基于扩散模型的通用射频信号生成模型。为了克服上述挑战，我们通过重新审视其理论基础、整体 DNN 架构和详细的算子设计，将现有的基于去噪的扩散模型扩展到时频域，从而使 RF-Diffusion 能够生成多样、高质量和时序射频数据。

• 时频扩散理论。我们首先提出时频扩散（Time-frequency Diffusion，TFD）理论，作为一种新的范式，以指导扩散模型提取和利用射频信号在时域和频域上的特征。具体来说，我们证明了扩散模型可以通过交替地在时域中添加噪声和在频域中模糊化，有效地破坏和恢复高质量的射频信号（§3）。

• 分层 Diffusion Transformer 设计。我们进一步重新设计了现有基于去噪的扩散模型的深度神经网络，使其与 TFD 兼容。所得到的 DNN 被命名为分层 Diffusion Transformer（Hierarchical Diffusion Transformer，HDT），从自上而下的视角来看，它通过解耦射频数据的时空维度，采用分层架构（i）来全面揭示时频细节；（ii）基于注意力的 Diffusion 块，利用增强的 Transformer 提取射频特征；以及（iii）复数值设计，以编码信号强度和相位信息。这三个关键设计协同工作，使射频扩散能够生成高质量的射频数据（§4）。

我们实现了 RF-Diffusion，并进行了包括 Wi-Fi 和 FMCW 信号合成在内的大量实验。为了清晰地理解其性能，表 1 直观地比较了 RF-Diffusion 生成的时频语图与相关工作生成的时频语图。评估结果表明，RF-Diffusion 生成的射频信号具有高保真度，相对于真实值实现了 81% 的平均结构相似性。这一性能超过了流行的生成模型，如 DDPM、DCGAN 和 CVAE 超过 18.6%。我们还在两个案例研究中展示了 RF-Diffusion 的性能：增强型 Wi-Fi 手势识别和 5G FDD 信道估计。通过使用 RF-Diffusion 作为数据增强器，现有的无线手势识别系统获得了显著的精度提升，范围从 4% 到 11%。当应用于信道估计任务时，与最先进的技术相比，RF-Diffusion 在 SNR 方面表现出显著的 5.97 dB 改进。

表1：示例。

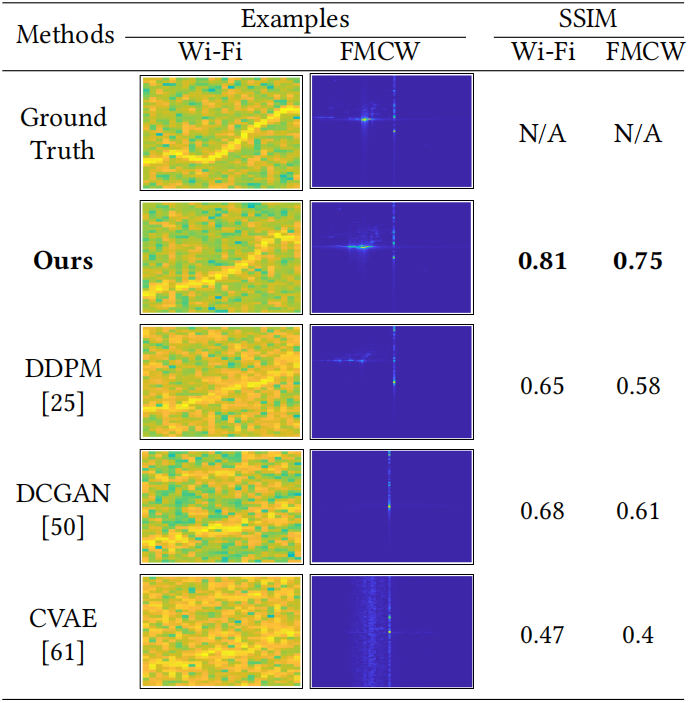总而言之，本文做出了以下贡献。（1）我们提出了 RF-Diffusion，这是第一个专为 RF 信号量身定制的生成扩散模型。RF-Diffusion 具有通用性，可用于广泛的基本无线任务，例如 RF 数据增强、信道估计和信号去噪，从而推动 AIGC 在 RF 领域发光。（2）我们提出了时频扩散理论（Time-Frequency Diffusion theory），这是超越传统基于去噪的扩散方法的高级演进。TFD 与其定制的分层扩散 Transformer（Hierarchical Diffusion Transformer，HDT）的集成，能够提高时间序列采样的精度，并均衡关注数据的频谱细节。（3）我们完整地实现了 RF-Diffusion。来自案例研究的广泛评估结果表明了 RF-Diffusion 的有效性。

社区贡献。 RF-Diffusion的代码和预训练模型已公开。我们的解决方案，部分或全部，可以为工业界和学术界提供一系列工具，以推动RF领域的人工智能内容生成（AIGC）。此外，它在突出数据频谱细微差别的同时处理时间序列采样的能力，具有超越无线社区的潜在优势，为视频、音频处理和其他时间序列相关的模式提供价值。

2 Overview

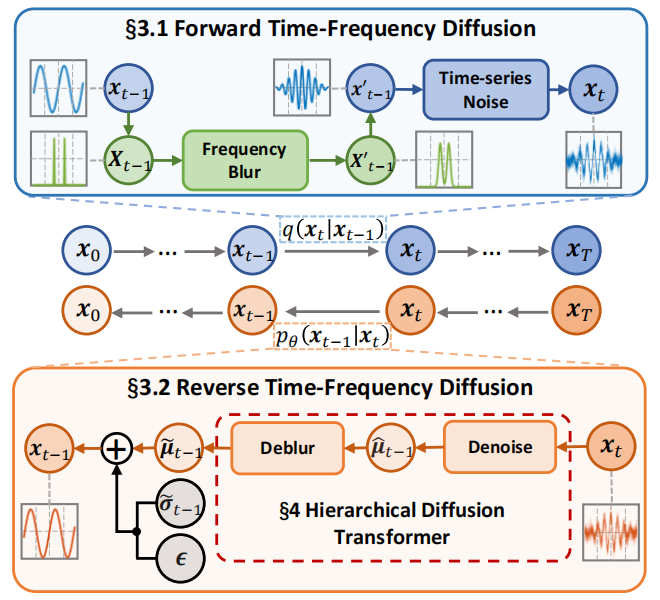图1：RF-Diffusion 概述。

我们提出了 RF-Diffusion，这是一种开创性的射频数据概率生成模型，它利用了扩散模型框架，如图 1 所示。RF-Diffusion 的核心在于，它与基于去噪的扩散模型原理相一致，采用双重过程方法：一个是将噪声整合到数据中的前向过程，以及一个是从噪声中生成数据的反向过程。然而，RF-Diffusion 通过两个创新特性来区分自身：

（i）RF-Diffusion 结合了所提出的时频扩散（§3）理论，以指导正向（即 $q({\mathbf{x}}_t|{\mathbf{x}}_{t-1})$）和反向（即 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$）过程中状态转移的每个阶段，使 RF-Diffusion 能够利用时域和频域中的 RF 信号信息。
（ii）RF-Diffusion 引入了分层 Diffusion Transformer（§4），这是一种重构的 DNN 模型，用于逆向生成过程，以符合时频扩散理论和RF信号的特性。

至于具体的数据流，RF-Diffusion 在前向方向的每个阶段，都会在时域中逐渐引入高斯噪声，并在频域中模糊频谱。随着扩散步骤 $t$ 的推进，原始 RF 信号 ${\mathbf{x}}_0$ 逐渐减弱，最终退化为噪声。在 TFD 理论中，我们证明了任何被破坏的信号 ${\mathbf{x}}_t$ 都可以使用参数化的逆过程恢复到其原始形式 ${\mathbf{x}}_0$。在时频域交替破坏过程的指导下，逆向恢复过程强调时域幅度精度和频域连续性，以实现时频高保真信号生成。

反之，HDT 被用作参数化模型来学习恢复过程。它解耦了高斯噪声和频谱模糊，从而有效地分别在空间去噪和时频去模糊阶段处理它们。在其训练过程中，HDT 将破坏的信号 ${\mathbf{x}}_t$ 作为模型输入，并使用先前扩散步骤的信号 ${\mathbf{x}}_{t-1}$ 来监督输出。一旦训练完成，RF-Diffusion 能够迭代地将完全退化的噪声转换回特定类型的信号。

3 Time-frequency Diffusion

在本节中，我们将介绍所提出的时频扩散（Time-Frequency Diffusion, TFD）过程。与目前流行的去噪扩散模型不同，时频扩散过程全面解决了无线信号数据中存在的两种潜在失真：1）由加性高斯噪声引起的幅度失真；2）由时间分辨率不足导致的频谱混叠。因此，学习到的逆过程不仅关注于精确重建单个样本的幅度，还关注于保持时序信号中的频谱分辨率。接下来，我们首先介绍前向破坏过程（§3.1），该过程共同消除时域和频域中的原始数据分布。在此基础上，我们描述如何逆转该过程（§3.2）并通过参数化模型进行拟合，这是我们条件生成（§3.3）任务的基础。

3.1 Forward Destruction Process

针对射频信号，提出了时频扩散模型，该模型可以将射频信号视为复值时间序列数据。因此，我们将信号视为一个二维复数张量 $\mathbf{x}\in {\mathbb{C}}^{M\times N}$，其中 $M$ 表示每个样本的空间维度，而 $N$ 表示时间序列的时间维度。

给定一个服从特定分布 ${\mathbf{x}}_0\sim q({\mathbf{x}}_0)$ 的信号，前向破坏过程会产生一系列随机变量 ${\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_T$ 。此过程中的每个扩散步骤都会从时域和频域扰乱原始分布。具体而言，从步骤 $t-1$ 到 $t$ 的前向扩散过程描述如下：

• 频率模糊。 为了消散原始信号的频谱细节，首先对时间维度执行傅里叶变换 $\mathfrak{F}(\cdot )$。随后，使用预定义的高斯卷积核 ${\mathbf{G}}_t$，对频谱执行循环卷积 $\ast$ 运算，从而产生模糊的频谱 ${\mathbf{G}}_t\ast \mathfrak{F}({\mathbf{x}}_{t-1})$。
• 时序噪声。 为了淹没信号的幅度细节，引入了复杂的标准高斯噪声 $\mathbf{ϵ}\sim \mathcal{C}\mathcal{N}(0,\mathbf{I})$，并使用预定义的参数 $\sqrt{{\alpha }_t}$ 进行加权求和，其中 ${\alpha }_t\in (0,1)$。

通过结合以上两个步骤，我们得到（公式 1）：

$${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathfrak{F}}^{-1}({\mathbf{G}}_t\ast \mathfrak{F}({\mathbf{x}}_{t-1}))+\sqrt{1-{\alpha }_t}\mathbf{ϵ},$$

其中 ${\mathfrak{F}}^{-1}(\cdot )$ 表示傅里叶逆变换。

为了确保时频扩散过程的实际可行性，至关重要的是，对于任何给定的步骤 $t\in [1,T]$，从 ${\mathbf{x}}_0$ 到 ${\mathbf{x}}_t$ 的过渡都可以在可接受的时间复杂度内执行，而不是涉及 $t$ 步的迭代。为了简化这个过程，利用了傅里叶变换和高斯函数的某些有利特性。基于卷积定理 [68]，我们有 ${\mathfrak{F}}^{-1}({\mathbf{G}}_t\ast \mathfrak{F}({\mathbf{x}}_{t-1}))={\mathfrak{F}}^{-1}({\mathbf{G}}_t){\mathbf{x}}_{t-1}$¹ 。因此，公式 1 中的运算可以表示为（公式 2）：

$${\mathbf{x}}_t=\sqrt{{\alpha }_t}{\mathbf{g}}_t{\mathbf{x}}_{t-1}+\sqrt{1-{\alpha }_t}\mathbf{ϵ},$$

其中 ${\mathbf{g}}_t={\mathfrak{F}}^{-1}({\mathbf{G}}_t)$ 仍然是一个高斯核，这意味着信号与高斯核在频域中的卷积可以等价地转换为信号与另一个高斯核在时域中的乘法。为了便于表示，令 ${\mathbf{\gamma }}_t=\sqrt{{\alpha }_t}{\mathbf{g}}_t$，且 ${\sigma }_t=\sqrt{1-{\alpha }_t}$，分别表示在步骤 $t$ 中信号 ${\mathbf{x}}_{t-1}$ 的权重和所添加噪声的标准差。

由于前向过程是一个马尔可夫链，通过递归应用公式 2 并结合重参数化技巧 [34]，可以得到原始信号 $x_0$ 和退化信号 $x_t$ 之间的关系（公式 3）：

$${\mathbf{x}}_t={\bar{\mathbf{\gamma }}}_t{\mathbf{x}}_0+\sum _{s=1}^t(\sqrt{1-{\alpha }_s}\frac{{\bar{\mathbf{\gamma }}}_t}{{\bar{\mathbf{\gamma }}}_s})\mathbf{ϵ}={\bar{\mathbf{\gamma }}}_t{\mathbf{x}}_0+{\bar{\mathbf{\sigma }}}_t\mathbf{ϵ},$$

其中 ${\bar{\mathbf{\gamma }}}_t={\prod }_{s=1}^t{\mathbf{\gamma }}_s={\mathbf{\gamma }}_t\cdots {\mathbf{\gamma }}_1$。由于 ${\alpha }_t$ 和 ${\mathbf{g}}_t$ 是对应于噪声和模糊调度策略的预定义超参数，因此任何 ${\bar{\mathbf{\gamma }}}_t$ 和 ${\bar{\mathbf{\sigma }}}_t$ 都是常数系数，分别表示原始信号的权重和添加噪声的标准差。因此，到任何步骤 $t$ 的前向破坏过程都可以快速完成，而无需迭代。用概率术语来说，本质上 ${\mathbf{x}}_t$ 服从以 ${\mathbf{x}}_0$ 为条件的非各向同性高斯分布（公式 4）：

$$q({\mathbf{x}}_t|{\mathbf{x}}_0)=\mathcal{C}\mathcal{N}({\mathbf{x}}_0;{\bar{\mathbf{\mu }}}_t,{\bar{\mathbf{\sigma }}}_t^2\mathbf{I}),$$

其中 ${\bar{\mathbf{\mu }}}_t={\bar{\mathbf{\gamma }}}_t{\mathbf{x}}_0$，且 ${\bar{\mathbf{\sigma }}}_t={\sum }_{s=1}^t(\sqrt{1-{\alpha }_s}\frac{{\bar{\mathbf{\gamma }}}_t}{{\bar{\mathbf{\gamma }}}_s})$。具体而言，向量 ${\bar{\mathbf{\gamma }}}_t$ 由不同的加权系数组成，每个系数以乘法方式应用于原始信号的时间维度，以执行加权调整。

在附录 A 中证明，随着扩散步骤 $t$ 的增加，原始信号逐渐被消除，并且 ${\mathbf{x}}_t$ 最终收敛到一个闭式噪声分布（公式 5）：

$$\underset{T\to \infty }{\lim }{\mathbf{x}}_T=\underset{T\to \infty }{\lim }\sum _{t=1}^T(\sqrt{1-{\alpha }_t}\frac{{\bar{\mathbf{\gamma }}}_T}{{\bar{\mathbf{\gamma }}}_t})\mathbf{ϵ}=\underset{T\to \infty }{\lim }{\bar{\mathbf{\sigma }}}_T\mathbf{ϵ},$$

其中 ${\bar{\mathbf{\sigma }}}_T={\sum }_{t=1}^T(\sqrt{1-{\alpha }_t}\frac{{\bar{\mathbf{\gamma }}}_T}{{\bar{\mathbf{\gamma }}}_t})\mathbf{ϵ}$ 由实际实现中预定义的噪声调度策略确定。

3.2 Reverse Restoration Process

恢复过程是破坏的逆过程，它逐渐消除噪声并恢复原始数据分布。

为了学习一个参数化的分布 $p_{\theta }({\mathbf{x}}_0)$，该分布近似于原始分布 $q({\mathbf{x}}_0)$，一种有效的方法是最小化它们的 Kullback-Leibler（KL）散度（公式 6）：

$$\begin{array}{rl}\theta & =\underset{\theta }{\mathrm{argmin}}{D}_{\mathrm{KL}}(q({\mathbf{x}}_0)\Vert p_{\theta }({\mathbf{x}}_0))\\ & =\underset{\theta }{\mathrm{argmin}}({\mathbb{E}}_{q({\mathbf{x}}_0)}[-\log p_{\theta }({\mathbf{x}}_0)]+{\mathbb{E}}_{q({\mathbf{x}}_0)}[\log q({\mathbf{x}}_0)])\\ & =\underset{\theta }{\mathrm{argmax}}{\mathbb{E}}_{q({\mathbf{x}}_0)}[\log p_{\theta }({\mathbf{x}}_0)].\end{array}$$

遗憾的是，通常情况下 $q({\mathbf{x}}_0)$ 难以计算 [35, 60]，因此 ${\mathbb{E}}_{q({\mathbf{x}}_0)}[\log p_{\theta }({\mathbf{x}}_0)]$ 无法显式表达。在先前工作的基础上 [25, 63]，我们通过最大化变分下界来近似分布。正如 [25] 中所述，公式 6 中的优化问题可以近似为（公式 7）：

$$\theta =\underset{\theta }{\mathrm{argmin}}{D}_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\Vert p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)),$$

其中 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$ 表示以 ${\mathbf{x}}_0$ 为条件的实际反向过程，而 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 表示由我们的模型拟合的反向过程。方程式 7 表明，重构原始数据分布的问题可以转化为拟合反向过程的问题。基于贝叶斯定理（附录 B）重写 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)$，我们证明它服从 ${\mathbf{x}}_{t-1}$上的高斯分布（公式 8）：

$$\begin{array}{rl}& q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\sim \mathcal{C}\mathcal{N}({\mathbf{x}}_{t-1};{\tilde{\mathbf{\mu }}}_{t-1},{\tilde{\mathbf{\sigma }}}_{t-1}^2\mathbf{I}),\\ {\tilde{\mathbf{\mu }}}_{t-1}& =\frac{1}{{\bar{\mathbf{\sigma }}}_t^2}({\mathbf{\gamma }}_t{\bar{\mathbf{\sigma }}}_{t-1}^2{\mathbf{x}}_t+{\bar{\mathbf{\gamma }}}_{t-1}{\mathbf{\sigma }}_t^2{\mathbf{x}}_0),{\tilde{\mathbf{\sigma }}}_{t-1}=\frac{{\bar{\mathbf{\sigma }}}_{t-1}}{{\bar{\mathbf{\sigma }}}_t}{\mathbf{\sigma }}_t.\end{array}$$

我们假设 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 是一个高斯马尔可夫过程（公式 9）：

$$p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)\sim \mathcal{C}\mathcal{N}({\mathbf{x}}_{t-1};{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t),{\mathbf{\sigma }}_{\theta }^2({\mathbf{x}}_t)\mathbf{I}).$$

因此，公式 7 中两个高斯分布的 KL 散度可以简化如下（公式 10）：

$$\begin{array}{rl}& D_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)\Vert p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t))\\ =& {\mathbb{E}}_{q({\mathbf{x}}_0)}[\frac{1}{2{\tilde{\mathbf{\sigma }}}_t^2}\Vert {\tilde{\mathbf{\mu }}}_{t-1}-{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t){\Vert }^2]+C.\end{array}$$

总而言之，参数化模型 $p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t)$ 的优化可以通过最小化 ${\mathbf{\mu }}_{\theta }$ 和 ${\tilde{\mathbf{\mu }}}_{t-1}$ 之间的均方误差（Mean Square Error，MSE）来实现。换句话说，如果一个模型能够从当前扩散步骤的输入 ${\mathbf{x}}_t$ 推断出前一步的均值 ${\tilde{\mathbf{\mu }}}_{t-1}$，那么它就胜任数据生成任务。

3.3 Conditional Generation

在大多数实际应用中，生成过程预计会受到条件标签 $\mathbf{c}$ 的引导，该标签指示生成的信号的特定类型（例如，对应于特定设备位置或人类活动的信号）。

将条件生成机制融入 RF-Diffusion 具有显著优势：（i）增强了实用性。条件生成机制使 RF-Diffusion 系统能够基于各种条件组合生成不同类别的信号。这消除了为每种信号类型训练单独模型的需要，从而显著提高了模型在实际应用中的效用。（ii）增加了信号多样性。一个训练良好的条件生成模型可以创建具有训练数据集条件标签空间内任何可想象的特征组合的多样化样本，这扩展了模型在初始训练集范围之外的泛化能力，确保数据增强有助于下游任务的性能改进。

在此上下文中，条件输入 $\mathbf{c}$ 定义了具体场景，包括各种房间、Tx-Rx 部署、人类活动类型和信号带宽。此输入指导生成过程，以产生与条件分布 $p_{\theta }(\mathbf{x}|\mathbf{c})$ 对齐的数据。条件正向和反向过程的示例如图 2 所示。

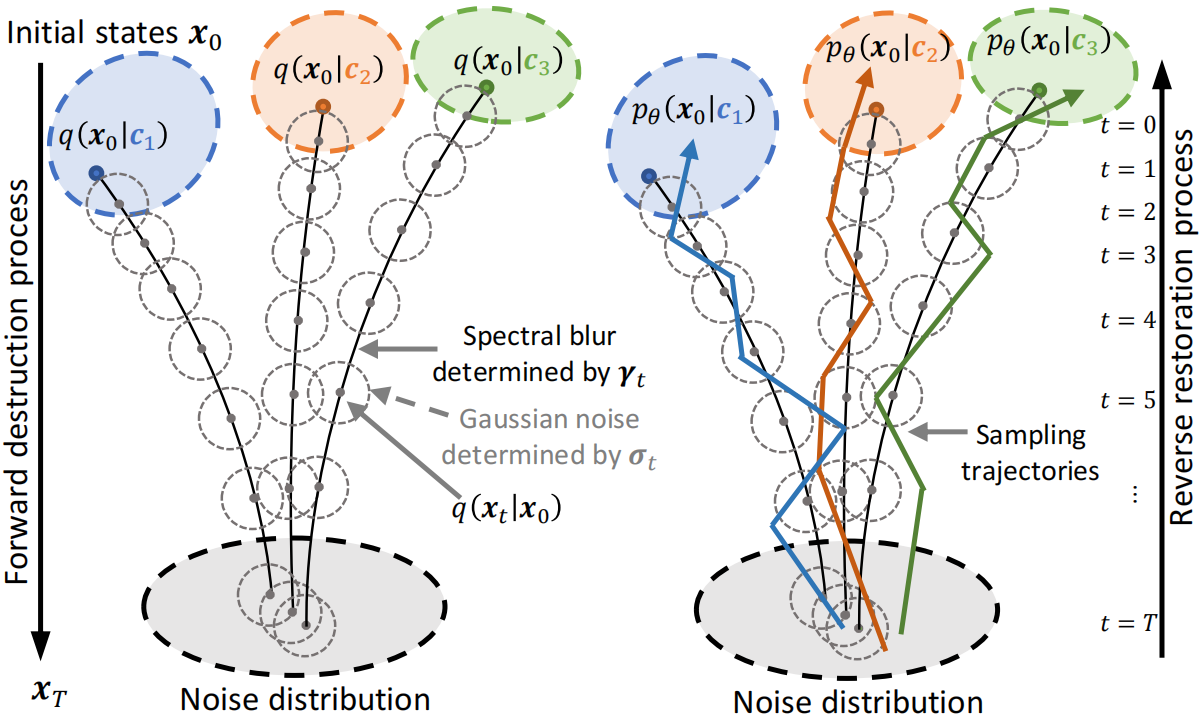图 2：条件正向和反向轨迹的图示。

在先前工作 [13, 27, 61] 结束后，我们直接将条件 $\mathbf{c}$ 纳入到前向过程方程 4 中和反向过程方程 8 中。并分别得到 $q({\mathbf{x}}_t|{\mathbf{x}}_0,\mathbf{c})$ 和 $q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{c})$ 。然后，通过结合方程 7 和方程10，优化可以写成（公式 11）：

$$\begin{array}{rl}\theta & =\underset{\theta }{\mathrm{argmin}}{D}_{\mathrm{KL}}(q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0,\mathbf{c})\Vert p_{\theta }({\mathbf{x}}_{t-1}|{\mathbf{x}}_t),\mathbf{c})\\ & =\underset{\theta }{\mathrm{argmin}}{\mathbb{E}}_{q({\mathbf{x}}_0)}[\Vert {\tilde{\mathbf{\mu }}}_{t-1}-{\mathbf{\mu }}_{\theta }({\mathbf{x}}_t({\mathbf{x}}_0,t,\mathbf{ϵ}),\mathbf{c}){\Vert }^2].\end{array}$$

用于修复的参数化模型的训练过程总结于算法 1。通过将所需的信号类型作为条件输入，训练后的模型可以从采样的噪声中迭代地合成原始信号。生成过程在算法 2 中进行了说明。

4 Hierarchical Diffusion Transformer

为了弥合时频理论与实用生成模型之间的差距，我们引入了一种分层扩散 Transformer (HDT)。我们提出的 HDT 融合了许多创新设计，使其与底层时频扩散理论相一致，并使其擅长于射频信号生成。我们首先介绍总体分层设计（§4.1），然后详细介绍我们提出的基于注意力的扩散块 (ADB) 的设计（§4.2）。为了解决复值信号生成的挑战，我们将经典 Transformer 块 [66] 的核心设计扩展到复数域（§4.3）。此外，我们提出相位调制编码 (PME)（§4.4），这是一种专为复值神经网络量身定制的新型位置编码方法。

4.1 Hierarchical Architecture

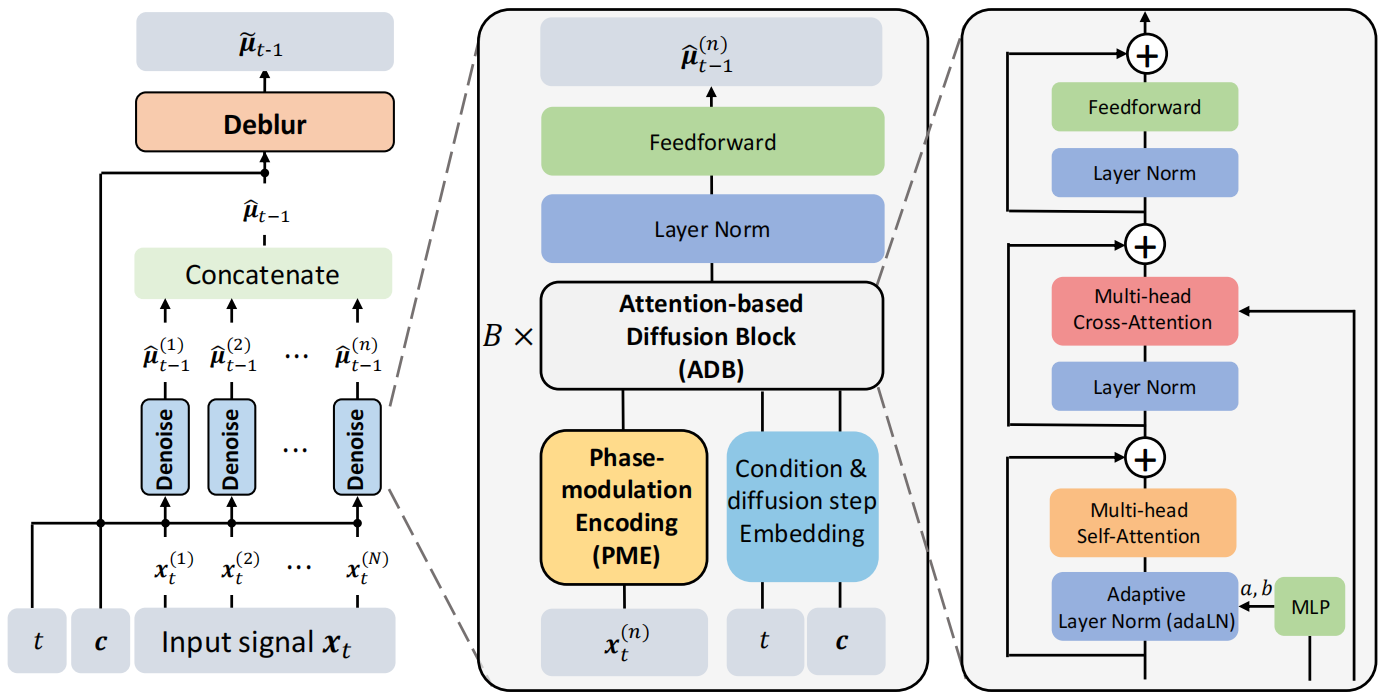图 3：分层扩散 Transformer 设计。

从顶层视角来看，HDT 采用分层架构来有效地解耦非各向同性噪声的估计。如图 3 所示，HDT 分为两个阶段：空间去噪和时频去模糊。

扩散步骤，表示为 $t$，被编码，从而告知模型关于当前输入的扩散水平。条件向量 $c$ 也进行编码。结合输入 ${\mathbf{x}}_t^{(n)}$，这些组成部分参与计算，力求辨别输入与其相关条件之间的潜在关联。

我们的观察是，非各向同性噪声可以分解为两个组成部分：1) 在空间维度 $M$ 和时间维度 $N$ 上独立的 Gaussian 噪声 $\mathbf{ϵ}$。2) 沿时间维度 $N$ 的不同信息和噪声权重（即 ${\bar{\gamma }}_t^{(n)}$ 和 ${\bar{\sigma }}_t^{(n)}$）。因此，通过将时间序列数据分割成单独的样本，我们得到 ${\mathbf{x}}_t^{(n)}={\bar{\gamma }}_t^{(n)}{\mathbf{x}}_0^{(n)}+{\bar{\sigma }}_t^{(n)}{\mathbf{ϵ}}^{(n)}$。在此，在每个样本中，信号和噪声权重都保持不变。因此，每个空间去噪模块独立地处理输入序列的单个样本 ${\mathbf{x}}_t^{(n)}$。在此阶段，去噪规避了由频谱模糊引起的时间域加权，专门关注引入到原始信息中的 Gaussian 噪声 ${\mathbf{ϵ}}^{(n)}$。这种方法与去噪扩散的原理 [25] 相呼应。

尽管空间去噪模块有效地减轻了噪声 $\mathbf{ϵ}$ 的影响，但其对每个样本的单独处理忽略了源于光谱模糊的时间加权效应。因此，将处理后的结果连接为 $\hat{\mathbf{\mu }}=[{\hat{\mathbf{\mu }}}^{(1)},\cdots ,{\hat{\mathbf{\mu }}}^{(N)}]$，并作为时频去模糊模块的序列输入，旨在估计平均值 ${\tilde{\mathbf{\mu }}}_{t-1}$。

4.2 Attention-based Diffusion Block

如图 3 所示，输入数据在去噪和去模糊阶段都通过一系列的 Transformer 块进行处理。我们引入了一种创新的基于注意力的扩散块，以联合分析噪声输入 ${\mathbf{x}}_t$、条件 $\mathbf{c}$ 和步长 $t$ 。

自注意力机制用于特征提取。 多头自注意力模块从噪声输入中捕获自相关特征，并提取信号中隐含的高级表示。与具有平移不变性的卷积层相比，注意力层对序列中每个样本的位置信息更敏感，因此能够更有效地恢复原始信号。

用于调节的交叉注意力机制。 为了增强条件生成能力，RF-Diffusion 引入了一个交叉注意力模块，以学习输入与其对应条件之间的潜在关联。该模块旨在直接捕捉输入和指定条件之间错综复杂的动态关系，从而提高生成信号的多样性和保真度。

扩散嵌入的自适应层归一化。 受现有条件生成模型中广泛使用的自适应归一化层 (adaLN) [47] 的启发 [9, 13]，我们探索用 adaLN 替换标准层归一化。我们没有直接学习维度比例 $a$ 和平移参数 $b$，而是从 $t$ 回归它们，从而将扩散步骤信息嵌入到我们的模型中。

4.3 Complex-Valued Module Design

为了有效地处理复值无线信号，RF-Diffusion 模型被设计成一个复值神经网络。为了方便复值运算，HDT 已经进行了一些调整。

复数值注意力模块。 在点积注意力机制中实现了两个关键改进，以适应复数计算：1) 查询向量和键向量的点积扩展到埃尔米特内积 ${\mathbf{q}}^{\mathrm{H}}\mathbf{k}$，它捕捉了复数空间中两个向量的相关性。这最大程度地保留了实部和虚部的有效信息。2) 鉴于 softmax 函数对实数进行运算，因此对其进行了调整，使其与复数向量兼容。具体而言，softmax 应用于点积的幅度，而相位信息保持不变。此修改保持了向量相关性的概率解释。用数学术语来说，复向量 $\mathbf{q}$ 和 $\mathbf{k}$ 的复数值注意力计算可以表示为（公式 12）：

$$\mathrm{softmax}(|{\mathbf{q}}^{\mathrm{H}}\mathbf{k}|)\exp (j\angle ({\mathbf{q}}^{\mathrm{H}}\mathbf{k})).$$

复数值前馈模块。 前馈模块主要由两个操作组成：线性变换和非线性激活。一个复数值线性变换可以分解为实数值线性变换 [64]。具体来说，对于复数值输入 $\mathbf{x}={\mathbf{x}}_r+j{\mathbf{x}}_i$，具有复数权重 $\mathbf{w}={\mathbf{w}}_r+j{\mathbf{w}}_i$ 和偏置 $\mathbf{b}={\mathbf{b}}_r+j{\mathbf{b}}_i$ 的变换可以写成如下形式（公式 13）：

$$\mathbf{w}\mathbf{x}+\mathbf{b}=\left[\begin{array}{l}\Re (\mathbf{w}\mathbf{x}+\mathbf{b})\\ \Im (\mathbf{w}\mathbf{x}+\mathbf{b})\end{array}\right]=\left[\begin{array}{rr}{\mathbf{w}}_r& -{\mathbf{w}}_i\\ {\mathbf{w}}_r& {\mathbf{w}}_i\end{array}\right]\left[\begin{array}{l}{\mathbf{x}}_r\\ {\mathbf{x}}_i\end{array}\right]+\left[\begin{array}{l}{\mathbf{b}}_r\\ {\mathbf{b}}_i\end{array}\right].$$

此外，将激活函数 $g(\cdot )$ 应用于复数值可以看作是分别激活实部和虚部：$g(\mathbf{x})=g({\mathbf{x}}_r)+jg({\mathbf{x}}_i)$。

4.4 Phase Modulation Encoding

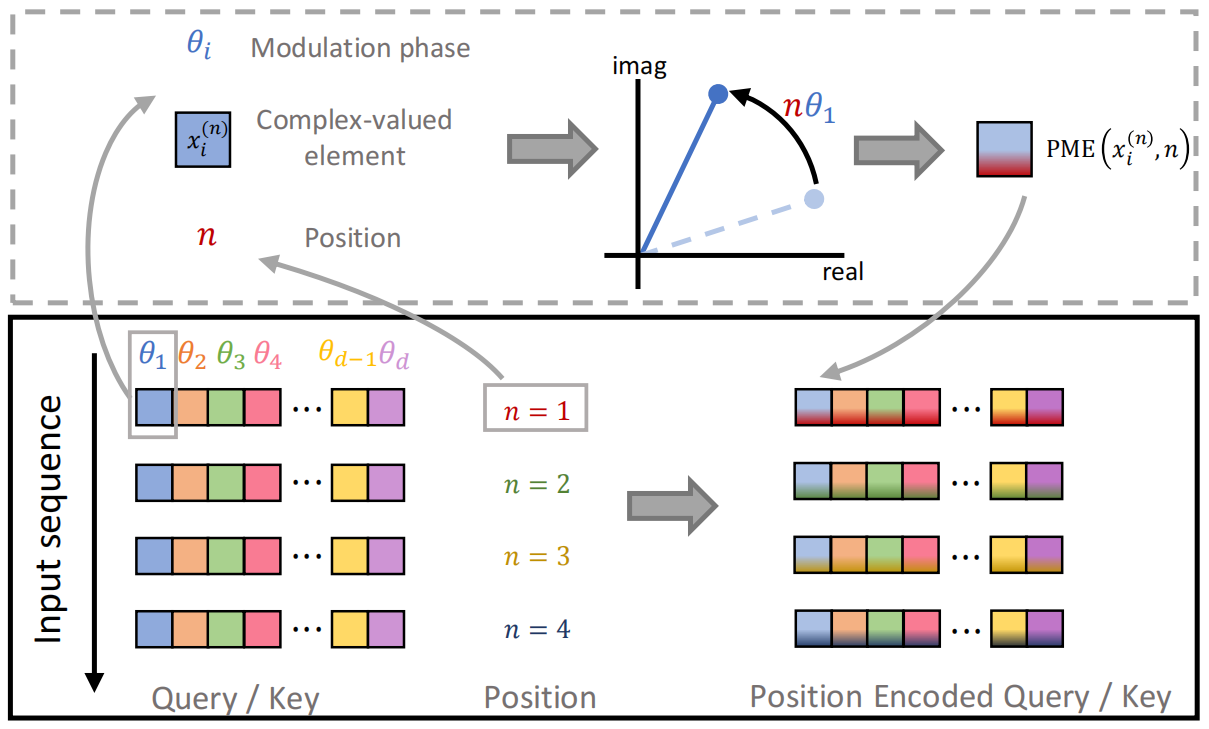图 4：相位调制编码示意图。

Transformer 网络利用注意力机制并行处理整个序列。然而，它缺乏辨别输入位置信息的固有能力。为了解决这个问题，我们引入了一种为复杂空间量身定制的创新相位调制编码（phase modulation encoding，PME）策略，作为 HDT 的位置编码方案。

如图 4 所示，假设序列中每个向量的最大维度为 $d$。对于序列中第 $n$ 个向量的第 $i$ 个元素，PME的运算方式如下（公式 14）：

$$\begin{array}{rl}\mathrm{PME}({\mathbf{x}}^{(n)}(i),n)& ={\mathbf{x}}_i^{(n)}\exp (jn{\theta }_i),\end{array}$$

其中 ${\theta }_i$ 由 ${\theta }_i=10000^{-\frac{i}{d}}$ 给出。此过程可以概念化为相位调制过程——本质上是根据序列中的位置 $n$ 将特定的相位偏移赋予原始数据。

PME 在计算过程中固有地解码相对位置，从而确立其在位置编码中的关键作用。具体而言，当对编码后的键向量 $\mathbf{k}$ 和查询向量 $\mathbf{q}$ 执行复数域注意力操作时，其等价于（公式 15）：

$$\begin{array}{r}\mathrm{PME}(\mathbf{q},n{)}^{\mathrm{H}}\mathrm{PME}(\mathbf{k},m)=\mathrm{PME}({\mathbf{q}}^{\mathrm{H}}\mathbf{k},m-n).\end{array}$$

因此，可以推导出相对位置信息 $m-n$。这使得我们的模型能够通过整合序列的位置细节来更熟练地学习。

5 Implementation

我们基于 PyTorch 实现了 RF-Diffusion，并在 8 个 NVIDIA GeForce 3090 GPU 上训练了我们的模型，同时结合了下面概述的关键实现技术。

指数移动平均。与大多数生成模型中的常见做法一致，我们采用指数移动平均（exponential moving average，EMA）机制，衰减率为 0.999。EMA 计算训练期间模型权重的滑动平均值，从而提高模型的鲁棒性。

权重初始化。我们在残差连接之前将每个最终层初始化为零，以加速大规模训练 [20]，并对其他层应用 Xavier 均匀初始化 [18]，这是基于 Transformer 的模型中的一种标准权重初始化技术 [15]。

超参数。我们使用 AdamW 优化器 [33, 39] 训练我们的模型，初始学习率为 $1\times 10^{-3}$。采用衰减因子为 0.5 的阶梯学习率调度器，以提高训练效率。在训练过程中，我们应用 0.1 的 dropout 率以减轻过拟合。

噪声调度策略。在我们的实现中，数据破坏率被设计为随着扩散过程的进行，从较低强度逐渐增加到较高强度。这旨在实现模型复杂性和生成质量之间的平衡 [35]。具体来说，我们将扩散过程配置为最多 $T=300$ 步。噪声系数 ${\beta }_t=\sqrt{1-{\alpha }_t}$ 被设置为从 $10^{-4}$ 线性增加到 0.03，即 ${\beta }_t=10^{-4}t$。与此同时，频域中高斯卷积核的标准差，记为 ${\mathbf{G}}_t$，被调整为从 $10^{-3}$ 线性增加到 0.3，从而促进在扩散步骤中对噪声的受控放大。

数据预处理。来自数据集的每个信号序列都被插值或降采样到一致的长度 512。这保证了模型输入长度的统一性。在输入到我们的模型之前，输入序列中的每个样本都通过平均信号功率进行归一化，这意味着每个样本都除以序列中所有样本的平均 L2 范数。

6 Evaluation

6.1 Experiment Design

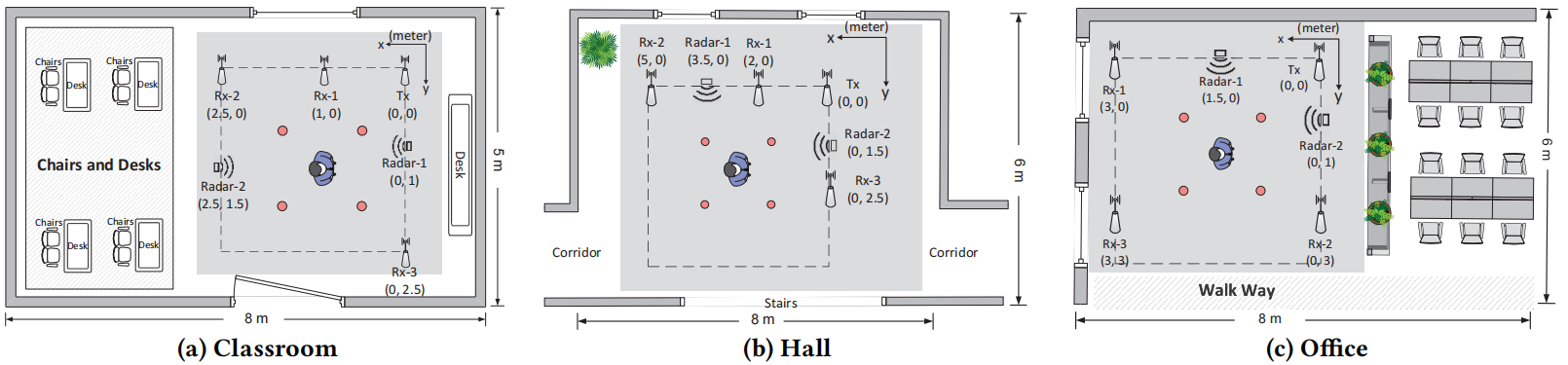图 5：实验场景。

6.1.1 数据收集 。如图 5 所示，我们的数据集包含在三种不同场景下收集的无线信号，这些场景在房间选择、设备位置和人为因素（包括人的位置、方向和活动）方面存在差异。我们将每个序列的条件标签编译成一个条件向量 $\mathbf{c}$，用于指导训练和采样阶段。我们的研究评估了 RF-Diffusion 在生成不同调制模式信号方面的能力，重点关注 Wi-Fi 和 FMCW 雷达信号，这两种信号是无线传感和通信的主要类型。

• Wi-Fi。我们基于工作在 5.825 GHz 频率和 40 MHz 带宽的商用网卡 IWL5300 采集 Wi-Fi 信号。发射器向 3 个接收器注入 Wi-Fi 数据包，以提取对应于环境的信道状态信息 (channel state information，CSI)。
• FMCW。FMCW 信号使用毫米波雷达 IWR1443 [29] 记录。该雷达设备可以放置在每个场景中的两个不同位置之一，工作频率范围为 77 GHz 至 81 GHz。

收集了超过 20,000 个 Wi-Fi 序列和 13,000 个 FMCW 序列。每个序列都有一个相关的条件标签，指示房间、设备放置、人体 ID、位置、方向和活动类型。本文中进行的所有实验均符合 IRB 政策。

6.1.2 比较方法 。我们将 RF-Diffusion 与三个具有代表性的数据生成模型进行比较：

• DDPM [25]。去噪扩散概率模型（denoising diffusion probabilistic model，DDPM）将高斯噪声引入原始数据，并随后学习逆转这一过程，从而从噪声中生成原始数据。
• DCGAN [50]。深度卷积生成对抗网络（deep convolutional generative adversarial network，DCGAN）是一种广为人知的 GAN。在 DCGAN 中，两个模型（即生成器和判别器）以对抗的方式同时训练。训练完成后，生成器可以生成能够令人信服地绕过判别器审查的数据。
• CVAE [62]。条件变分自编码器（conditional variational autoencoder，CVAE）学习数据的高斯隐式表示，从而实现数据生成。该方法被广泛应用于传感 [21] 和通信 [38] 系统中，以合成无线特征。

为了使它们适应射频信号，我们使用复值神经网络重新实现了该模型 [64]。

6.1.3 评估指标 。为了进行全面的评估，我们采用了两种指标，这两种指标均被先前研究广泛用于评估数据驱动的生成模型 [2, 13, 25, 30, 44]。鉴于尚未建立生成模型的明确“金标准”，这些指标是目前最具权威性的指标。

• SSIM [67]：结构相似性指标（Structural Similarity Index Measure，SSIM）是一种通过分析两个样本的均值和协方差来衡量它们之间相似性的重要标准。我们已经将 SSIM 调整为适用于复数域，使其适合评估复数值信号。
• FID [24]：Fréchet 初始距离 (Fréchet Inception Distance，FID) 通过测量真实数据和合成数据的高级特征之间的 Fréchet 距离来评估生成模型。我们采用预训练的 STFNets [73] 作为特征提取器，以更好地适应无线信号的属性。

6.2 Overall Generation Quality

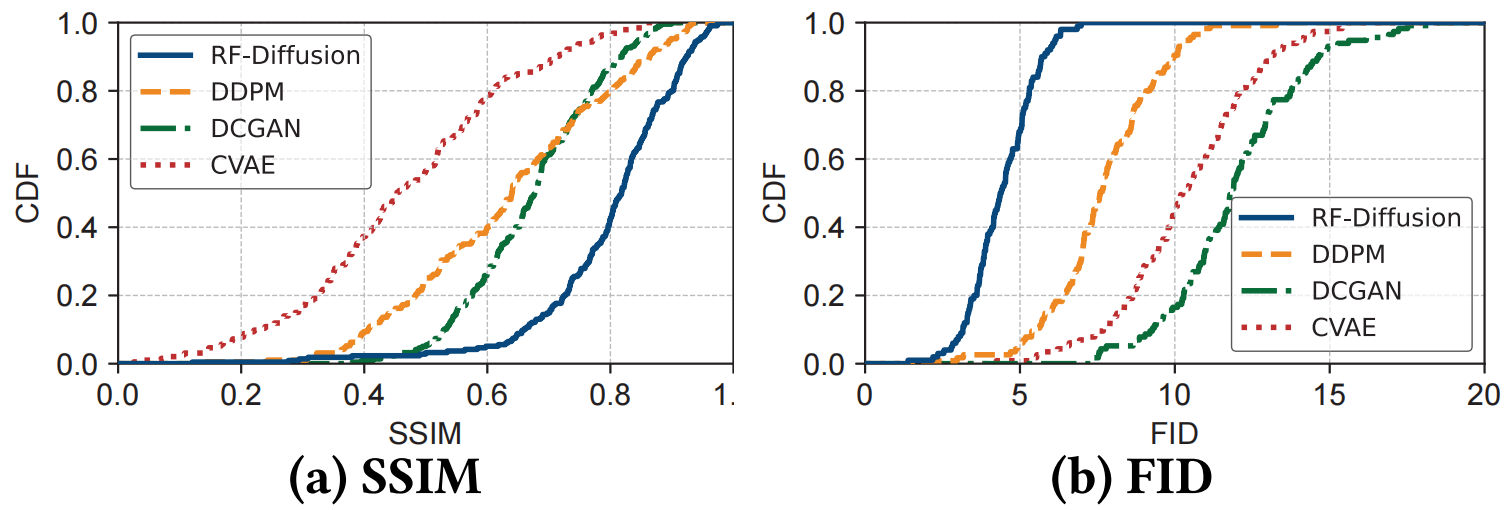图 6：Wi-Fi 信号生成质量。
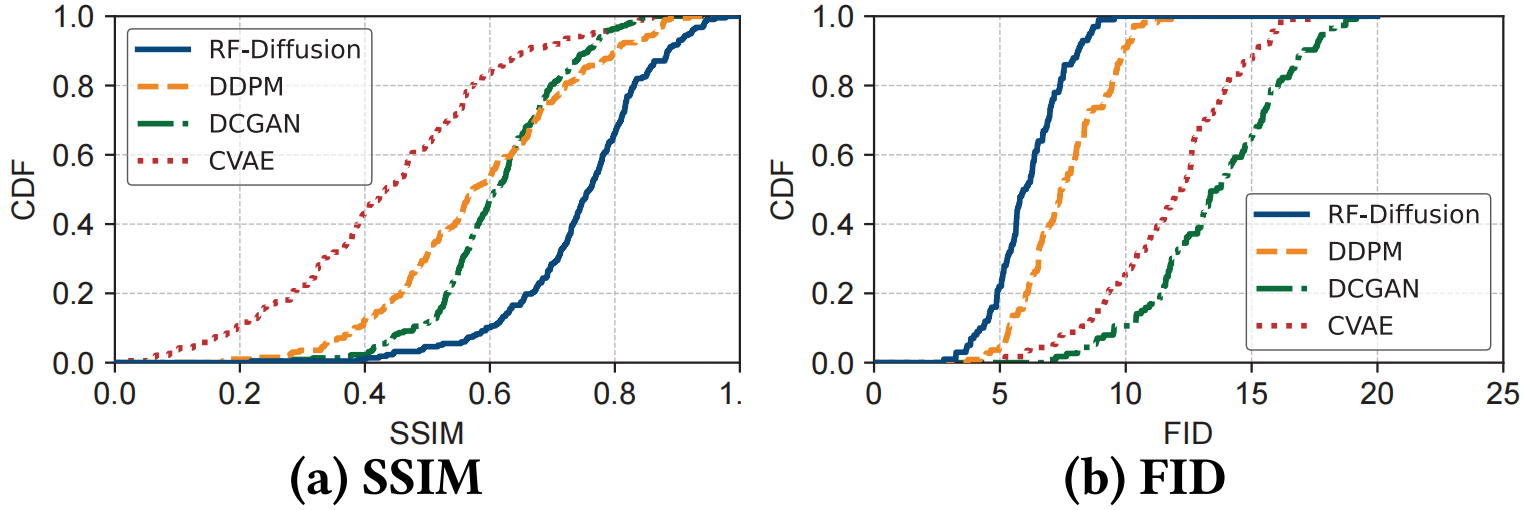图 7：FMCW 信号生成质量。

RF-Diffusion 在 Wi-Fi 和 FMCW 信号上的评估结果分别如图 6 和图 7 所示。如图所示，我们提出的 RF-Diffusion 已证明在两种指标上均优于对比方法。

具体而言，如图 6 所示，RF-Diffusion 生成的 Wi-Fi 信号的平均 SSIM 为 0.81，分别超过DDPM、DCGAN 和 CVAE 25.4%、18.6% 和 71.3%。RF-Diffusion 实现了 4.42 的 FID，分别优于上述比较方法 42.4%、63.0% 和 57.3%。

在生成高保真 FMCW 信号方面，RF-Diffusion 也优于对比方法。如图 7 所示，RF-Diffusion 生成的 FMCW 信号的平均 SSIM 达到 0.75，平均 FID 达到 6.10。

RF-Diffusion 的出色性能可归因于以下几个关键因素：1) RF-Diffusion 采用的我们提出的时频扩散强调优化射频信号的频谱，从而在生成的信号中保留更精细的频谱细节，这对于其他方法来说难以捕捉。2) 通过其迭代生成方法，RF-Diffusion 通过多步近似实现对数据细节的精确重建，从而产生更高质量的生成数据。3) 与同时优化两个模型的 DCGAN 相比，RF-Diffusion 的损失函数更精简，其训练过程更稳定，从而确保了生成信号中更丰富的多样性，并有助于获得值得称赞的 FID 分数。

6.3 Micro-benchmarks

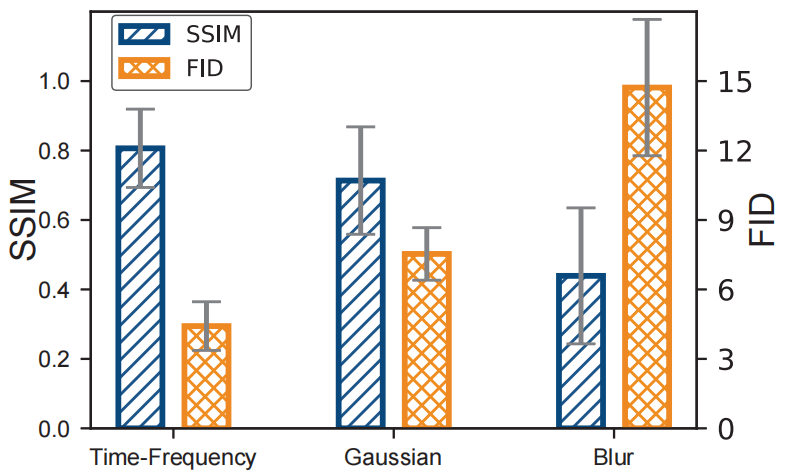图 8：扩散方法的影响。

6.3.1 扩散方法的影响。为了验证我们提出的时频扩散理论的有效性，我们保留了 RF-Diffusion 的网络模型架构，但将时频扩散过程替换为两种替代方案：1) 高斯扩散，类似于 DDPM，仅将高斯噪声引入到信号幅度中；2) 模糊扩散，仅执行频谱模糊。如图 8 所示，我们的时频扩散理论在 SSIM 和 FID 指标方面始终优于其他两种方法。具体而言，时频扩散、高斯扩散和模糊扩散的 SSIM 值分别为 0.81、0.71 和 0.45。这意味着时频扩散比高斯扩散的 SSIM 提高了 13.9%，比模糊扩散显著提高了 79.2%。在 FID 方面，时频扩散分别超过其他两种方法 41.3% 和 83.5%。结果表明，时频扩散理论成功地将两种扩散方法结合在正交空间上，从而实现了互补的优势。

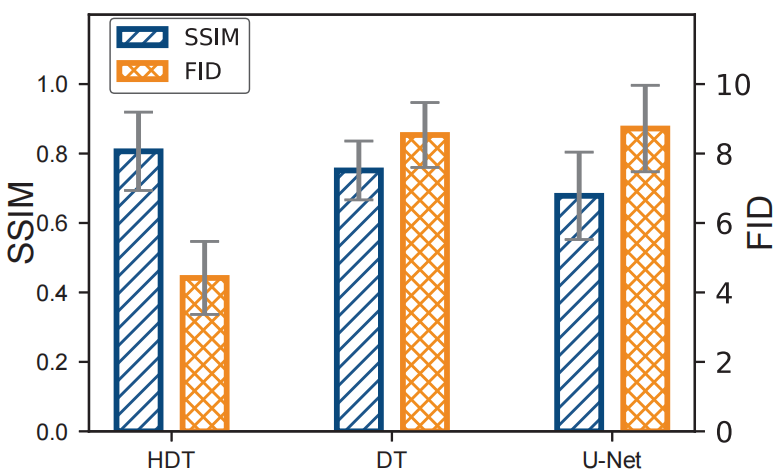图 9：网络设计的影响。

6.3.2 网络设计的影响。为了展示我们提出的分层扩散 Transformer（HDT）的优势，我们将其与以下模型进行比较：1）单阶段扩散 Transformer（SDT），它是 HDT 的简化形式，仅有一个阶段用于端到端的数据恢复；以及2）U-Net [55]，这是流行扩散模型中的常见选择。如图 9 所示，我们提出的 HDT 优于 SDT 和 U-Net。具体而言，HDT、SDT 和 U-Net 的 SSIM 分别为0.81、0.75 和 0.68。这表明 HDT 的 SSIM 比 SDT 提高了 7.7%，并且比 U-Net 显著提高了 18.9%。当使用 FID 指标评估时，HDT 继续领先，分别比 SDT 和 U-Net高出 48.2% 和 49.3%。这种卓越的性能得益于以下几个方面：1）与 SDT 相比，HDT 可以有效地解耦扩散过程中引入的非各向同性噪声，并通过两个连续的阶段消除它；2）与平移不变的 U-Net 相比，HDT 的 Transformer 架构可以有效地区分不同时间的信号特征，从而实现更精确的信号生成。

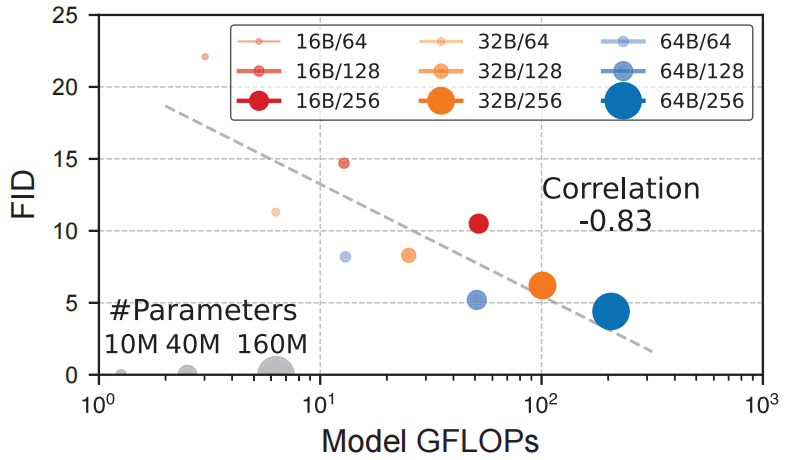图 10：可扩展性分析。

6.3.3 可扩展性分析。可扩展性是指模型通过增大尺寸来提升其性能的能力，这对于像 RF-Diffusion 这样的大型生成模型至关重要。为了验证 RF-Diffusion 的可扩展性，我们训练了 9 个不同尺寸的模型，探索了不同数量的基于注意力的扩散块（16B、32B、64B）和隐藏维度（64、128、256）。图 10 表明，RF-Diffusion 的 FID 性能与模型参数和 GFLOPs 密切相关，这表明扩大模型参数和增加模型计算是获得更好性能的关键因素。预计增加模型尺寸将进一步提升 RF-Diffusion 的性能。

7 Case Study

本节展示了 RF-Diffusion 如何在两个不同的下游任务中使无线研究受益：基于 Wi-Fi 的手势识别和 5G FDD 信道估计。

7.1 Wi-Fi Gesture Recognition

无线传感 [12, 17, 71, 74] 已成为一个重要的研究焦点。通过充当数据增强器，RF-Diffusion 可以提升现有无线传感系统的性能，同时保留原始模型结构，无需任何修改。特别地，我们的方法包括首先使用真实世界的数据集训练 RF-Diffusion。随后，RF-Diffusion 生成指定类型的合成射频信号，并由条件标签引导。这些合成样本随后与原始数据集集成，共同用于训练无线传感模型。RF-Diffusion 增强的解决方案和基线都从根本上基于相同的真实世界数据集，确保了公平的比较，因为 RF-Diffusion 本身是在这个真实世界数据集上训练的，并且没有涉及任何额外的数据。

我们通过基于 Wi-Fi 的手势识别案例来说明这种方法，并评估通过将 RF-Diffusion 集成到已建立的手势识别模型中所获得的性能提升。

7.1.1 实验设计。我们选择两种不同类型的基于 Wi-Fi 的模型进行全面评估：

• Widar 3.0 [78] 是一个基于物理原理的手势识别模型。它首先从原始信号中提取特征，然后通过深度神经网络进行识别。
• EI [31] 是一种数据驱动的端到端人类活动识别模型，它以原始信号作为输入。

我们利用来自 Widar 3.0 [78] 的公开数据集来评估性能。此评估涵盖了 RF-Diffusion 和比较方法（§6.1.2）被用作数据增强器的场景。

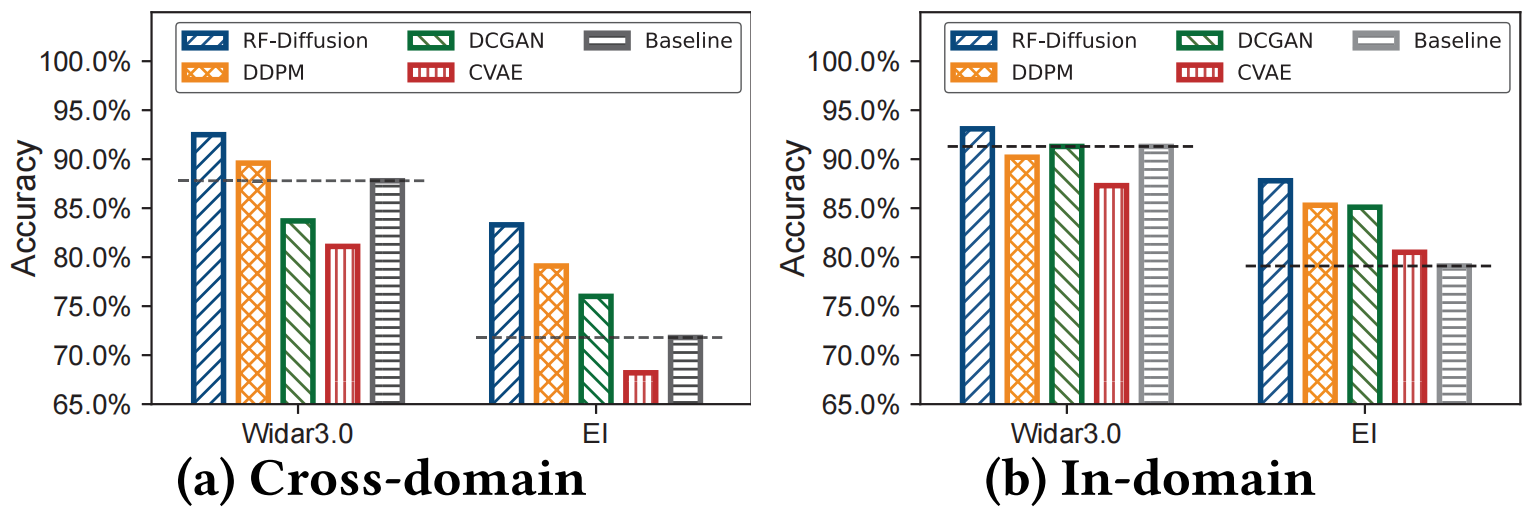图 11：增强 Wi-Fi 传感的性能。

7.1.2 跨域评估。我们首先评估当训练集和测试集来自不同域（即，房间、设备放置、人体位置、方向等）时的感知性能，这是现实世界无线感知系统部署中的常见情况。我们使用预训练的 RF-Diffusion 合成与真实世界数据集等量的数据。随后，合成数据集和真实数据集都用于训练。如图 11a 所示，集成 RF-Diffusion 分别使 Widar 3.0 和 EI 的性能提高了 4.7% 和 11.5%。集成 DDPM 带来的性能提升相对有限，分别只有 1.8% 和 7.3%。此外，由于合成数据分布与原始数据分布存在偏差，集成 DCGAN 或 CVAE 可能会导致识别准确率下降。

与 Widar 3.0 相比，EI模型获得了更显著的改进，原因在于：1）作为一个端到端 DNN，EI 对数据量和数据多样性更敏感；2）以数据驱动方式生成的无线信号中的信息在转换为物理特征时，无法在 Widar 3.0 中得到充分利用。

总之，RF-Diffusion 在以下两个方面增强了无线传感系统跨域性能：

• 增强数据多样性。具有更高多样性的合成训练数据可以避免模型过拟合，从而隐式地提高模型的领域泛化能力。
• 特征蒸馏。生成模型 RF-Diffusion 通过合成训练数据，隐式地将其学习到的信号特征传递给识别模型，从而有助于提高性能。

7.1.3 域内评估。在域内场景中，训练和测试数据来自同一领域。如图 11b 所示，RF-Diffusion 的集成使 Widar 3.0 和 EI 的性能分别提高了 1.8% 和 8.7%。总的来说，与跨域场景相比，域内情况下的性能提升相对适中。这归因于多样化的合成训练数据对增强模型在同一领域内的性能影响有限。对于域内测试，即使使用 DCGAN 生成的较少多样性的合成数据，也可以实现明显的性能提升。

7.1.4 合成数据比例的影响。我们进一步研究用于训练的合成数据比例的影响，以提供更多见解。我们评估了 Widar 3.0 和 EI 在跨域（cross-domain，CD）和域内（in-domain，ID）情况下的表现。

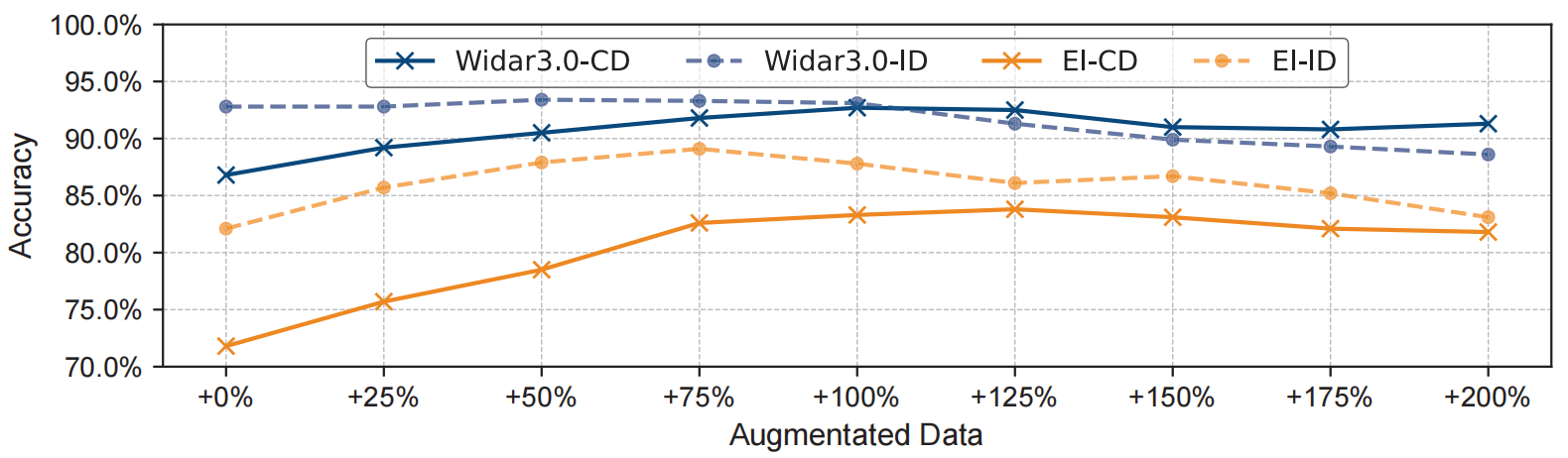图 12：合成数据比例的影响。

如图 12 所示，我们向真实世界数据集引入不同数量的合成数据（从 +25% 到 +200%），用于识别模型的联合训练。值得注意的是，随着合成数据量的增加，识别准确率的趋势呈现出先上升后下降的态势。具体而言，在跨域情况下，Widar 3.0 在 +100% 合成数据时达到最高准确率 92.7%，而 EI 在 +125% 合成数据时达到最高准确率 83.8%。在域内情况下， Widar 3.0 在 +50% 合成数据时达到最高准确率 93.4%，而 EI 在 +75% 合成数据时达到最高准确率 89.1%。从这些统计结果中，我们得出以下见解：1) 对于大多数无线识别模型，明智地将合成数据纳入训练集可以有效地提高模型性能。2) 过度引入合成数据可能会使训练数据分布偏离原始分布，从而降低识别准确率。3) 与域内场景相比，跨域场景需要向训练集中注入更多的合成数据才能实现最佳模型性能。4) 数据驱动的端到端模型（例如，EI）从 RF-Diffusion 促进的数据增强中获得更显著的益处。

7.2 5G FDD Channel Estimation

在本节中，我们将讨论 RF-Diffusion 如何在 5G 中实现频分双工（Frequency Domain Duplex，FDD）系统的信道估计，其中上行链路和下行链路传输在不同的频段上运行。因此，两个链路信道相等的互易性原则不再成立 [38]。为了估计下行链路信道状态，客户端设备必须从具有大规模天线阵列的基站接收额外的符号，并将估计结果发回，从而导致不可持续的开销。为了解决这个问题，大量的研究致力于通过观察上行链路信道状态信息来预测下行链路信道。例如，FNN [5] 和 FIRE [38] 分别利用全连接网络和 VAE 将估计的 CSI 从上行链路传输到下行链路。

我们发现，通过将上行链路 CSI 用作条件输入，RF-Diffusion 展示了以生成方式估计下行链路信道 CSI 的能力。具体而言，在 RF-Diffusion 中，下行链路 CSI ${\mathbf{x}}_{\mathrm{down}}$ 作为生成的目标数据，而上行链路 CSI 被编码为条件 ${\mathbf{c}}_{\mathrm{up}}$ 并输入到模型中。经过训练的 RF-Diffusion 学习 ${\mathbf{c}}_{\mathrm{up}}$ 和 ${\mathbf{x}}_{\mathrm{down}}$ 之间的相关性，从而完成信道估计任务。这种有效性植根于共享传播路径的假设，即认为两个链路信道都由相同的底层物理环境塑造 [28, 65]。

7.2.1 实验设计。我们的评估基于公开可用的数据集 Argos [58]，这是一个真实的 MIMO 数据集，在一个复杂的环境中收集，具有大量的非视距（NLoS）传播。每个 CSI 帧包含 52 个子载波。与之前的工作类似 [38, 76]，我们指定最初的 26 个子载波用于上行链路信道，而剩余的 26 个子载波分配给下行链路信道。为了进行全面的评估，我们将我们的方法与三种不同类型的信道估计解决方案进行比较：

• NeRF${}^2$ [76] 基于神经网络，从上行链路信道状态隐式地学习信号传播环境，然后估计下行链路信道。
• FIRE [38] 是一个基于 VAE 的信道估计系统，它将上行链路信道 CSI 压缩成潜在空间表示，并进一步将其转换为下行链路信道估计。
• Codebook [32]，通常在 3GPP 物理信道标准的标准实现中使用 [1]，要求基站和客户端都维护一个使用预定义规则创建的向量码本。客户端在本地测量信道，选择最接近的码本向量，并将相应的索引发送回基站。

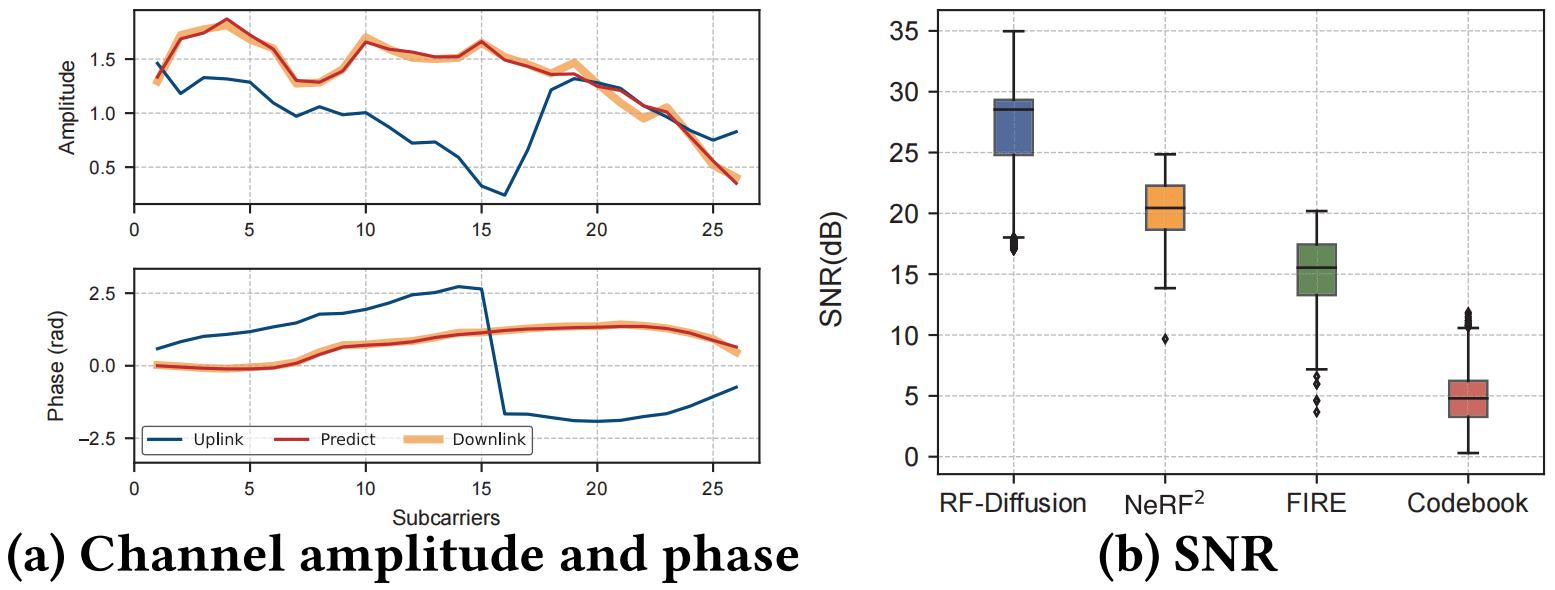图 13：信道估计性能。

7.2.2 信道估计精度。如图 13a 所示，当我们把蓝色上行链路 CSI 作为条件输入到训练好的 RF-Diffusion 中时，会输出红色下行链路估计，该估计与真实的下行链路信道状态非常吻合。信道估计精度的评估采用信噪比（Signal-to-Noise Ratio，SNR）指标 [38, 76]。该指标通过以下公式衡量估计的下行链路信道 ${\mathbf{x}}_{\mathrm{est}}$ 与真实值 ${\mathbf{x}}_{\mathrm{down}}$ 之间的一致性（公式 16）：

$$\mathrm{SNR}=-10{\log }_{10}\left(\frac{\Vert {\mathbf{x}}_{\mathrm{down}}-{\mathbf{x}}_{\mathrm{est}}{\Vert }^2}{\Vert {\mathbf{x}}_{\mathrm{down}}{\Vert }^2}\right).$$

较高的正信噪比（SNR）对应于预测信道与真实值之间更强的接近度。如图 13b 所示，RF-Diffusion 在所有比较方法中实现了最高的信噪比，平均信噪比为 27.01，分别优于 NeRF${}^2$ 和 FIRE 34.6% 和 77.5%，并且与基于码本的标准实现相比，实现了超过 5 倍的性能提升。

NeRF${}^2$ 表现不佳的原因可归因于其将信号传播空间视为一个时不变系统，这种描述可能不适用于实际情况。基于 VAE 的 FIRE 和基于 codebook 的方法在信道状态底层分布的细粒度表征方面存在不足。相比之下，RF-Diffusion 巧妙地学习了上行链路和下行链路信道之间错综复杂的相关性，利用其强大的建模能力来实现高度精确的信道估计。

8 Related Work

下面我们简要回顾一下相关工作。

扩散概率模型。扩散概率模型 [60, 70] 已经成为一种强大的新型深度生成模型家族，在包括图像合成、点云补全和自然语言处理等诸多应用中取得了破纪录的性能 [13]。其中最著名的扩散模型之一是 DDPM [60]，它通过注入高斯噪声逐步破坏数据，然后学习逆转这个过程以实现高保真样本生成。在此基础上，DDIM [44] 加快了反向采样，而 LDM [54] 在潜在空间中进行扩散以减少计算开销。上述方案已被广泛应用于图像超分辨率 [26, 57]、图像修复 [40] 和风格迁移 [56] 等各种任务中。最近的研究 [37, 52] 已经成功地将模糊和加性噪声相结合应用于图像，产生了令人满意的结果。尽管扩散模型最初是为图像生成而提出的，但其多功能性已扩展到其他领域，包括点云补全 [41, 79]、文本生成 [3, 19]、音频合成 [11, 35] 等。此外，扩散模型在多模态生成方面具有巨大的潜力。通过集成预训练的语言模型 [49]，扩散模型在文本到图像 [45, 51] 和文本到音频 [48] 任务中取得了令人印象深刻的性能。

相比之下，RF-Diffusion 是首个专为无线信号生成量身定制的扩散模型。它引入了一种创新的时频扩散过程，该过程在两个正交域中调节噪声和模糊，从而涵盖了无线信号的时间和频谱复杂性。通过生成高保真信号，RFDiffusion 有益于无线应用，如 Wi-Fi 感知和 5G 信道估计。

无线系统中的信号生成。传统的无线信号生成方案主要基于建模和仿真。特别地，这些方法涉及利用激光雷达扫描的 3D 模型，并采用电磁（electromagnetic，EM）射线追踪技术 [42] 来模拟无线信号的分布。最近的研究 [10, 36, 75] 将基于视觉的人体重建技术与信号传播模型相结合，从而能够生成与人体交互的无线信号。不幸的是，上述方案未能对结构材料和物理特性进行建模，这限制了它们在实际应用中的性能。最近提出的 NeRF${}^2$ [76]基于深度神经网络学习信号传播空间的属性，然后完成信号生成任务。然而，NeRF${}^2$ 仅限于特定的静态场景，并且在动态的真实场景中性能下降。RF-EATS [21] 和 FallDar [72] 采用变分自编码器（VAE）来提取环境独立特征，从而增强了无线传感模型的泛化能力。此外，其他研究已经利用生成对抗网络（GAN）来生成多普勒频谱 [16]。其他研究工作已经使用 GANs [6, 14] 或 VAEs [8, 38] 解决了无线通信系统中的信道估计问题。然而，由于其有限的表示能力，基于 GAN 和 VAE 的解决方案难以忠实地表征原始无线信号的内在属性。因此，上述系统仅适用于特定任务，缺乏通用无线数据生成的能力。

相比之下，RF-Diffusion 作为一种通用的无线信号生成模型，即使在动态场景中，也能高效地生成高保真度的精细信号。

9 Discussion and Future Work

RF-Diffusion 是在基于扩散的射频信号生成方面的一项开创性尝试，并且在各个方面都有持续研究的空间。

• RF-Diffusion 用于数据驱动的下游任务。大量的实践 [4, 23, 59, 77] 表明，来自生成模型的合成数据显著增强了数据驱动的下游任务。作为一个条件生成模型，RF-Diffusion 有效地捕捉了代表性特征及其新颖的组合，同时随机化了非必要的细节。这种方法允许生成超出数据集初始范围的创新数据样本，从而提高下游模型的泛化能力。本文专门探索并实验了应用 RF-Diffusion 来增强 Wi-Fi 手势识别，展示了其潜力。然而，RF-Diffusion 的适用性扩展到无线通信和传感中的任何数据驱动任务。
• RF-Diffusion 作为一种仿真工具。作为一个概率生成模型，RF-Diffusion 的运行独立于任何信号传播假设，并且不需要对环境进行预建模。这种灵活性意味着，虽然 RF-Diffusion 为信号合成提供了新的机会，但在所有情况下，它可能无法达到与传统信号仿真工具相同的稳定性和精度。RF-Diffusion 并非旨在取代仿真工具，而是引入一种新颖的、数据驱动的信号合成方法，这种方法在复杂和动态的环境中尤其有价值，例如存在人类活动的室内空间，在这些环境中，精确建模提出了挑战。
• 自回归信号生成。RF-Diffusion，一种非自回归生成模型，将时间序列视为一个统一的实体进行处理，因此需要对变长序列进行降采样和插值，这限制了其通用性。诸如 GPT 等自回归模型的出现，为时间序列信号生成引入了替代方法，提高了对不同长度序列的适应性，并能够有效地探索时间相关性特征。

10 Conclusion

本文介绍了 RF-Diffusion，这是一种开创性的生成扩散模型，专为射频信号设计。RF-Diffusion 通过采用一种新颖的时频扩散过程，擅长生成高保真时序信号。此过程捕获了射频信号在空间、时间和频率域中的复杂特征。然后，该理论框架被转化为基于分层扩散 Transformer 的实用生成模型。RF-Diffusion 表现出卓越的通用性。它在重要的无线任务中具有巨大的潜力，从提高无线传感系统的精度，到估计通信系统中的信道状态，从而揭示了 AIGC 在无线研究中的应用。

A Convergence of Forward Destruction Process

当 $T\to \infty$ 时，前向过程收敛到与原始信号无关的分布。上述命题等价于以下两个条件：（1）${\lim }_{T\to \infty }{\bar{\mathbf{\mu }}}_T=0$，（2）${\lim }_{T\to \infty }{\bar{\mathbf{\sigma }}}_T<\infty$。我们找到了上述情况成立的充分条件：${\mathbf{\gamma }}_t=\sqrt{{\alpha }_t}{\mathbf{g}}_t$ 中的所有元素都应小于 1，即 $\forall n,{\gamma }_t^{(n)}<1$。在此条件下，根据公式 3，${\lim }_{T\to \infty }{\bar{\mathbf{\mu }}}_T={\lim }_{T\to \infty }{\bar{\mathbf{\gamma }}}_T{\mathbf{x}}_0=0$ 成立。设 ${\alpha }_{\min }=\min ({\alpha }_t),t\in [1,T]$ 且 ${\gamma }_{\max }^{(n)}=\max ({\gamma }_t^{(n)})$ 且 ${\mathbf{\gamma }}_{\max }=({\gamma }_{\max }^{(1)},\dots ,{\gamma }_{\max }^{(N)})$。可以证明（公式 17）：

$$\begin{array}{rl}& \underset{T\to \infty }{\lim }{\bar{\mathbf{\sigma }}}_T=\underset{T\to \infty }{\lim }\sum _{t=1}^T(\sqrt{1-{\alpha }_t}\frac{{\bar{\mathbf{\gamma }}}_T}{{\bar{\mathbf{\gamma }}}_t})\\ & \le \sqrt{1-{\alpha }_{\min }}\underset{T\to \infty }{\lim }\sum _{t=1}^T({\mathbf{\gamma }}_{\max }{)}^{t-1}=\frac{\sqrt{1-{\alpha }_{\min }}}{1-{\mathbf{\gamma }}_{\max }}<\infty \end{array}$$

B Reverse Process Distribution

基于贝叶斯定理，我们得到：

$$\begin{array}{rl}& q({\mathbf{x}}_{t-1}|{\mathbf{x}}_t,{\mathbf{x}}_0)=q({\mathbf{x}}_t|{\mathbf{x}}_{t-1},{\mathbf{x}}_0)\frac{q({\mathbf{x}}_{t-1}|{\mathbf{x}}_0)}{q({\mathbf{x}}_t|{\mathbf{x}}_0)}\\ \propto & \exp (-\frac{1}{2}(\frac{({\mathbf{x}}_t-{\mathbf{\gamma }}_t{\mathbf{x}}_{t-1}{)}^2}{{\mathbf{\sigma }}_t^2}+\frac{({\mathbf{x}}_{t-1}-{\bar{\mathbf{\gamma }}}_{t-1}{\mathbf{x}}_0{)}^2}{{\bar{\mathbf{\sigma }}}_{t-1}^2}-\frac{({\mathbf{x}}_t-{\bar{\mathbf{\gamma }}}_t{\mathbf{x}}_0{)}^2}{{\bar{\mathbf{\sigma }}}_t^2}))\\ =& \exp (((\frac{{\mathbf{\gamma }}_t}{{\mathbf{\sigma }}_t}{)}^2+(\frac{1}{{\bar{\mathbf{\sigma }}}_{t-1}}{)}^2){\mathbf{x}}_{t-1}^2-(\frac{2{\mathbf{\gamma }}_t}{{\mathbf{\sigma }}_t^2}{\mathbf{x}}_t+\frac{2{\bar{\mathbf{\gamma }}}_{t-1}}{{\bar{\mathbf{\sigma }}}_{t-1}^2}{\mathbf{x}}_0){\mathbf{x}}_{t-1}+C({\mathbf{x}}_t,{\mathbf{x}}_0)),\end{array}$$

其中使用了递归关系：${\bar{\mathbf{\sigma }}}_t^2={\mathbf{\gamma }}_t^2{\bar{\mathbf{\sigma }}}_{t-1}^2+{\mathbf{\sigma }}_t^2$，该关系可以通过结合公式 2 和公式 3 推断得出。

---

1. 本文中向量乘法默认采用元素级乘积。 ↩︎