动态规划——状压DP经典题目
状压dp
前言
小明的宠物袋
题目分析
合法矩阵类状压DP
动态规划三阶段
第一个阶段定义dp数组
(1)缩小规模。我要求的是一个大小为n*m的合法矩阵,我可以选择一行一行的确定矩阵是什么样子的,也就是我要考虑n行,那么n行就是一个规模,dp[i]表示当前考虑了矩阵的前i行
(2)考虑限制。
a.每一行没有相邻的宠物。
b.每一列没有相邻的宠物。
c.原来有食物的地方不能添加宠物。
对于限制a,因为我是一行一行的考虑的,我可以预处理出来所有合法行,遍历的时候只遍历合法行。一行有m列,每一列的取值是0或者1,0表示没有放宠物,1表示放了宠物,可能出现的行有2m2^m2m种情况。一行其实就是一个二进制数,二进制数的范围是[0,(1<<m)-1]。合法行就是没有相邻的1,如果行i是合法的,那么我将行i左移1位,移位后的行与移位前的行对应位置上一定不会存在都是1的情况,否则就是不合法的(可以参考下图)。移位后的行与移位前的行相与其实就是每个位置上的数和它相邻位置上的数相与,如果存在相邻位为1,结果就不会是0,否则结果是0。
所以可以通过i&(i<<1)是否等于0判断该行是否合法。关键代码如下,
for(int i = 0;i < (1<<m);i++) book[i]=(i&(i<<1))==0;
对于限制b,每次添加行时,我需要判断该行的添加是否会导致某些列不合法。这里要怎么判断呢?假设第i-1行是j,当前行是k,如果添加后出现了j与k的对应位同时为1的情况,即j&k!=0,则表示当前行的添加不合法。所以我需要知道第i-1行是什么样子的,需要一个维度来表示。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j。
对于限制c,假设当前添加行的状态是j,而矩阵的原始状态是map[i],在map[i]中原本放置宠物的地方用1表示。如果对应位置同时出现了两个1就表示,我把宠物放在了原本有宠物的地方,这是不行的,即j&map[i]!=0,就是不合法的。
(3)定义dp数组。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j的情况下放入的最多宠物数。
第二个阶段推导状态转移方程
对于第i行,我可以从所有的合法行里面选择,转移状态如下
dp[i][j]=max(dp[i−1][k]+w,dp[i][j])dp[i][j]=max(dp[i-1][k]+w,dp[i][j])dp[i][j]=max(dp[i−1][k]+w,dp[i][j])
前i行肯定是从前i-1行的某个状态转移,如果上述转移成立,那么在第i-1行为k的情况下,我是可以放j的,也就是满足限制b,同时对于原始矩阵的第i行我也可以放j,满足限制c。那么这个www表示的是j行放入的宠物个数,也就是j的二进制里面1的个数,可以直接用java的函数表示,也可以预处理出一个数组nums[j]表示j的二进制里面1的个数。
第三个阶段写代码
(1)dp数组的初始化。最初的状态是一个宠物也没有就是0,对于Java而言不用特意管。
(2)递推dp数组。
a.第一层for循环表示的是规模 i表示当前考虑了前i行 1:n
b.第二层for循环表示的是限制 j表示所有可能出现的行 0:(1<<m)-1
这里要判断一下j是否是合法的,并且j是否和原来的矩阵冲突了,即限制a和限制c
c.第三层for循环表示的是dp数组的转移点 即第i-1行所有的状态 0:(1<<m)-1
这里要判断一下j和k是否冲突即限制b
(3)表示答案。max(dp[n][j])max(dp[n][j])max(dp[n][j])
题目代码
import java.util.Scanner;
public class Main{/** 移位前:1010101010* 移位后:0101010100* * 移位前:10110* 移位后:01100*/
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();long dp[][] = new long[n+1][1<<m];int map[] = new int[n+1];for(int i = 1;i <= n;i++)for(int j = 0;j < m;j++) {int u = scanner.nextInt();if(u==1) map[i] |= (1<<j);}int mod = (int) 1e8;boolean book[] = new boolean[1<<m];for(int i = 0;i < (1<<m);i++) book[i]=(i&(i<<1))==0;for(int i = 1;i <= n;i++) {for(int j = 0;j < (1<<m);j++) {//011 000 001 010 if((map[i]&j)==0&&book[j]) {//for(int k = 0;k < (1<<m);k++) {//if((k&j)==0) dp[i][j] = Math.max(dp[i][j],Integer.bitCount(j)+dp[i-1][k]);}}}}long res = 0;for(int i = 0;i < (1<<m);i++) res = Math.max(res,dp[n][i]);System.out.println(res);
}
}
#include <iostream>
#include <vector>
#include <algorithm>
#include <bitset>using namespace std;const int MOD = 1e8;int main() {int n, m;cin >> n >> m;// dp[i][j] 表示处理到第i行,状态为j时的最大值vector<vector<long>> dp(n+1, vector<long>(1<<m, 0));vector<int> map(n+1, 0); // 存储每行的不可用位置// 读取输入数据并构建地图for(int i = 1; i <= n; ++i) {for(int j = 0; j < m; ++j) {int u;cin >> u;if(u == 1) map[i] |= (1 << j); // 标记不可用位置}}// 预处理合法状态:检查状态是否没有相邻的1vector<bool> valid(1<<m, false);for(int i = 0; i < (1<<m); ++i) {valid[i] = (i & (i << 1)) == 0;}// 动态规划处理for(int i = 1; i <= n; ++i) {for(int j = 0; j < (1<<m); ++j) {// 检查状态是否合法且不与地图冲突if((map[i] & j) == 0 && valid[j]) {for(int k = 0; k < (1<<m); ++k) {// 检查上下行状态是否冲突if((k & j) == 0) {dp[i][j] = max(dp[i][j], (long)__builtin_popcount(j) + dp[i-1][k]);}}}}}// 找出最终结果long res = 0;for(int i = 0; i < (1<<m); ++i) {res = max(res, dp[n][i]);}cout << res << endl;return 0;
}
def main():import sysinput = sys.stdin.readdata = input().split()idx = 0n = int(data[idx])m = int(data[idx+1])idx += 2MOD = 10**8dp = [[0] * (1 << m) for _ in range(n+1)]map_data = [0] * (n+1)# 读取输入数据并构建地图for i in range(1, n+1):for j in range(m):u = int(data[idx])idx += 1if u == 1:map_data[i] |= (1 << j)# 预处理合法状态valid = [False] * (1 << m)for i in range(1 << m):valid[i] = (i & (i << 1)) == 0# 动态规划处理for i in range(1, n+1):for j in range(1 << m):# 检查状态是否合法且不与地图冲突if (map_data[i] & j) == 0 and valid[j]:for k in range(1 << m):# 检查上下行状态是否冲突if (k & j) == 0:count = bin(j).count('1')dp[i][j] = max(dp[i][j], count + dp[i-1][k])# 找出最终结果res = max(dp[n])print(res)if __name__ == "__main__":main()
状压dp
前言
小明的宠物袋
题目分析
合法矩阵类状压DP
动态规划三阶段
第一个阶段定义dp数组
(1)缩小规模。我要求的是一个大小为n*m的合法矩阵,我可以选择一行一行的确定矩阵是什么样子的,也就是我要考虑n行,那么n行就是一个规模,dp[i]表示当前考虑了矩阵的前i行
(2)考虑限制。
a.每一行没有相邻的宠物。
b.每一列没有相邻的宠物。
c.原来有食物的地方不能添加宠物。
对于限制a,因为我是一行一行的考虑的,我可以预处理出来所有合法行,遍历的时候只遍历合法行。一行有m列,每一列的取值是0或者1,0表示没有放宠物,1表示放了宠物,可能出现的行有2m2^m2m种情况。一行其实就是一个二进制数,二进制数的范围是[0,(1<<m)-1]。合法行就是没有相邻的1,如果行i是合法的,那么我将行i左移1位,移位后的行与移位前的行对应位置上一定不会存在都是1的情况,否则就是不合法的(可以参考下图)。移位后的行与移位前的行相与其实就是每个位置上的数和它相邻位置上的数相与,如果存在相邻位为1,结果就不会是0,否则结果是0。
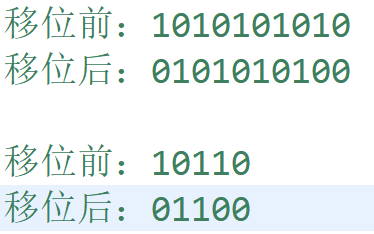
所以可以通过i&(i<<1)是否等于0判断该行是否合法。关键代码如下,
for(int i = 0;i < (1<<m);i++) book[i]=(i&(i<<1))==0;
对于限制b,每次添加行时,我需要判断该行的添加是否会导致某些列不合法。这里要怎么判断呢?假设第i-1行是j,当前行是k,如果添加后出现了j与k的对应位同时为1的情况,即j&k!=0,则表示当前行的添加不合法。所以我需要知道第i-1行是什么样子的,需要一个维度来表示。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j。
对于限制c,假设当前添加行的状态是j,而矩阵的原始状态是map[i],在map[i]中原本放置宠物的地方用1表示。如果对应位置同时出现了两个1就表示,我把宠物放在了原本有宠物的地方,这是不行的,即j&map[i]!=0,就是不合法的。
(3)定义dp数组。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j的情况下放入的最多宠物数。
第二个阶段推导状态转移方程
对于第i行,我可以从所有的合法行里面选择,转移状态如下
dp[i][j]=max(dp[i−1][k]+w,dp[i][j])dp[i][j]=max(dp[i-1][k]+w,dp[i][j])dp[i][j]=max(dp[i−1][k]+w,dp[i][j])
前i行肯定是从前i-1行的某个状态转移,如果上述转移成立,那么在第i-1行为k的情况下,我是可以放j的,也就是满足限制b,同时对于原始矩阵的第i行我也可以放j,满足限制c。那么这个www表示的是j行放入的宠物个数,也就是j的二进制里面1的个数,可以直接用java的函数表示,也可以预处理出一个数组nums[j]表示j的二进制里面1的个数。
第三个阶段写代码
(1)dp数组的初始化。最初的状态是一个宠物也没有就是0,对于Java而言不用特意管。
(2)递推dp数组。
a.第一层for循环表示的是规模 i表示当前考虑了前i行 1:n
b.第二层for循环表示的是限制 j表示所有可能出现的行 0:(1<<m)-1
这里要判断一下j是否是合法的,并且j是否和原来的矩阵冲突了,即限制a和限制c
c.第三层for循环表示的是dp数组的转移点 即第i-1行所有的状态 0:(1<<m)-1
这里要判断一下j和k是否冲突即限制b
(3)表示答案。max(dp[n][j])max(dp[n][j])max(dp[n][j])
题目代码
import java.util.Scanner;
public class Main{/** 移位前:1010101010* 移位后:0101010100* * 移位前:10110* 移位后:01100*/
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();int m = scanner.nextInt();long dp[][] = new long[n+1][1<<m];int map[] = new int[n+1];for(int i = 1;i <= n;i++)for(int j = 0;j < m;j++) {int u = scanner.nextInt();if(u==1) map[i] |= (1<<j);}int mod = (int) 1e8;boolean book[] = new boolean[1<<m];for(int i = 0;i < (1<<m);i++) book[i]=(i&(i<<1))==0;for(int i = 1;i <= n;i++) {for(int j = 0;j < (1<<m);j++) {//011 000 001 010 if((map[i]&j)==0&&book[j]) {//for(int k = 0;k < (1<<m);k++) {//if((k&j)==0) dp[i][j] = Math.max(dp[i][j],Integer.bitCount(j)+dp[i-1][k]);}}}}long res = 0;for(int i = 0;i < (1<<m);i++) res = Math.max(res,dp[n][i]);System.out.println(res);
}
}
#include <iostream>
#include <vector>
#include <algorithm>
#include <bitset>using namespace std;const int MOD = 1e8;int main() {int n, m;cin >> n >> m;// dp[i][j] 表示处理到第i行,状态为j时的最大值vector<vector<long>> dp(n+1, vector<long>(1<<m, 0));vector<int> map(n+1, 0); // 存储每行的不可用位置// 读取输入数据并构建地图for(int i = 1; i <= n; ++i) {for(int j = 0; j < m; ++j) {int u;cin >> u;if(u == 1) map[i] |= (1 << j); // 标记不可用位置}}// 预处理合法状态:检查状态是否没有相邻的1vector<bool> valid(1<<m, false);for(int i = 0; i < (1<<m); ++i) {valid[i] = (i & (i << 1)) == 0;}// 动态规划处理for(int i = 1; i <= n; ++i) {for(int j = 0; j < (1<<m); ++j) {// 检查状态是否合法且不与地图冲突if((map[i] & j) == 0 && valid[j]) {for(int k = 0; k < (1<<m); ++k) {// 检查上下行状态是否冲突if((k & j) == 0) {dp[i][j] = max(dp[i][j], (long)__builtin_popcount(j) + dp[i-1][k]);}}}}}// 找出最终结果long res = 0;for(int i = 0; i < (1<<m); ++i) {res = max(res, dp[n][i]);}cout << res << endl;return 0;
}
def main():import sysinput = sys.stdin.readdata = input().split()idx = 0n = int(data[idx])m = int(data[idx+1])idx += 2MOD = 10**8dp = [[0] * (1 << m) for _ in range(n+1)]map_data = [0] * (n+1)# 读取输入数据并构建地图for i in range(1, n+1):for j in range(m):u = int(data[idx])idx += 1if u == 1:map_data[i] |= (1 << j)# 预处理合法状态valid = [False] * (1 << m)for i in range(1 << m):valid[i] = (i & (i << 1)) == 0# 动态规划处理for i in range(1, n+1):for j in range(1 << m):# 检查状态是否合法且不与地图冲突if (map_data[i] & j) == 0 and valid[j]:for k in range(1 << m):# 检查上下行状态是否冲突if (k & j) == 0:count = bin(j).count('1')dp[i][j] = max(dp[i][j], count + dp[i-1][k])# 找出最终结果res = max(dp[n])print(res)if __name__ == "__main__":main()
交错矩阵——合法矩阵类状压DP
题目分析
动态规划三阶段
第一个阶段定义dp数组
(1)缩小规模。我要求的是一个大小为n*m的合法矩阵,我可以选择一行一行的确定矩阵是什么样子的,也就是我要考虑n行,那么n行就是一个规模,dp[i]表示当前考虑了矩阵的前i行
(2)考虑限制。
a.每一行没有相邻的1。
b.每一列没有相邻的1。
对于限制a,因为我是一行一行的考虑的,我可以预处理出来所有合法行,遍历的时候只遍历合法行。一行有m列,每一列的取值是0或者1,可能出现的行有2m2^m2m种情况。一行其实就是一个二进制数,二进制数的范围是[0,(1<<m)-1]。合法行就是没有相邻的1,如果行i是合法的,那么我将行i左移1位,移位后的行与移位前的行对应位置上一定不会存在都是1的情况,否则就是不合法的(可以参考下图)。移位后的行与移位前的行相与其实就是每个位置上的数和它相邻位置上的数相与,如果存在相邻位为1,结果就不会是0,否则结果是0。
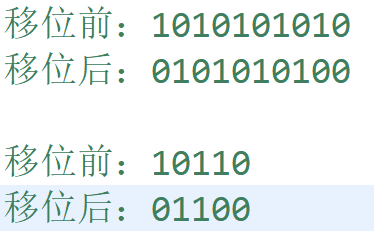
所以可以通过i&(i<<1)是否等于0判断该行是否合法。关键代码如下,
private static boolean check(int u) {//检查u是否是合法行if((u&(u<<1))==0) return true;return false;
}
对于限制b,每次添加行时,我需要判断该行的添加是否会导致某些列不合法。这里要怎么判断呢?假设第i-1是j,当前行是k,如果添加后出现了j与k的对应位同时为1的情况,即j&k!=0,则表示当前行的添加不合法。所以我需要知道第i-1行是什么样子的,需要一个维度来表示。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j。
(3)定义dp数组。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j的情况下的方案数。
第二个阶段推导状态转移方程
对于第i行,我可以从所有的合法行里面选择,转移状态如下
dp[i][j]+=dp[i−1][k]dp[i][j]+=dp[i-1][k]dp[i][j]+=dp[i−1][k]
前i行肯定是从前i-1行的某个状态转移,如果上述转移成立,那么在第i-1行为k的情况下,我是可以放j的,也就是满足限制b。注意这里是加,不是乘。
第三个阶段写代码
(1)dp数组的初始化。最初的状态是只有一行,那么不受列的约束,所有的合法行都是可以的,那么dp[1][i]=1dp[1][i]=1dp[1][i]=1。
(2)递推dp数组。
a.第一层for循环表示的是规模 i表示当前考虑了前i行 1:n
b.第二层for循环表示的是限制 j表示所有可能出现的合法行
c.第三层for循环表示的是dp数组的转移点 即第i-1行所有的状态k
这里要判断一下j和k是否冲突即限制b
(3)表示答案。res+=dp[n][j(所有的合法行)]res+=dp[n][j(所有的合法行)]res+=dp[n][j(所有的合法行)]
题目代码
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.Scanner;
public class Main{static long dp[][];static int n,m;static List<Integer> list = new ArrayList<Integer>();
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);n = scanner.nextInt();m = scanner.nextInt();dp = new long[n+1][1<<m];for(int i = 0;i < (1<<m);i++) {if(check(i)) list.add(i);}for(Integer i :list) dp[1][i]=1;for(int i = 2;i <= n;i++) {for(Integer j:list) {for(Integer k:list) {if((j&k)==0) {dp[i][j] += dp[i-1][k];}}}}long res = 0;for(Integer e:list) {res += dp[n][e];}System.out.println(res);
}
private static boolean check(int u) {//1100 1000if((u&(u<<1))==0) return true;return false;
}
}
威震华夏——合法矩阵类状压DP
题目分析
动态规划三阶段
第一个阶段定义dp数组
(1)缩小规模。我要求的是一个大小为n*m的合法矩阵,我可以选择一行一行的确定矩阵是什么样子的,也就是我要考虑n行,那么n行就是一个规模,dp[i]表示当前考虑了矩阵的前i行
(2)考虑限制。
a.军队不能埋伏在空地点(0),只能埋伏在树林(1)。
b.任意两支军队的埋伏点不能相邻。
对于限制a,我需要存图,然后我当前填的行和图中的对应行相与,如果所填行对应位置都是放在树林里的,地图中1的位置会与1相与,也可以与0相与。与1相与得1,与0相与得0,不改变我填入行的值。地图中0的位置只会与0相与,得0,不改变我填入行的值。但是如果出现了地图中0的位置与1相与,得0,会改变我填入行的值,并且此时是不合法的。如下代码,
(map[i]&j)==j
对于限制b,我先考虑在行上没有相邻的埋伏点,因为我是一行一行的考虑的,我可以预处理出来所有合法行,遍历的时候只遍历合法行。一行有m列,每一列的取值是0或者1,可能出现的行有2m2^m2m种情况。一行其实就是一个二进制数,二进制数的范围是[0,(1<<m)-1]。合法行就是没有相邻的1,如果行i是合法的,那么我将行i左移1位,移位后的行与移位前的行对应位置上一定不会存在都是1的情况,否则就是不合法的(可以参考下图)。移位后的行与移位前的行相与其实就是每个位置上的数和它相邻位置上的数相与,如果存在相邻位为1,结果就不会是0,否则结果是0。
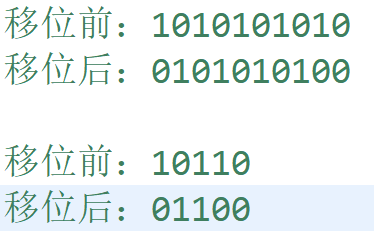
所以可以通过i&(i<<1)是否等于0判断该行是否合法。关键代码如下,
boolean book[] = new boolean[1<<n];
for(int i = 0;i < (1<<n);i++) book[i]=(i&(i<<1))==0;
对于列上没有相邻点,每次添加行时,我需要判断该行的添加是否会导致某些列不合法。这里要怎么判断呢?假设第i-1是j,当前行是k,如果添加后出现了j与k的对应位同时为1的情况,即j&k!=0,则表示当前行的添加不合法。所以我需要知道第i-1行是什么样子的,需要一个维度来表示。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j。
(3)定义dp数组。dp[i][j]dp[i][j]dp[i][j]表示当前考虑了矩阵的前i行并且第i行是j的情况下的方案数。
第二个阶段推导状态转移方程
对于第i行,我可以从所有的合法行里面选择,转移状态如下
dp[i][j]+=dp[i−1][k]dp[i][j]+=dp[i-1][k]dp[i][j]+=dp[i−1][k]
前i行肯定是从前i-1行的某个状态转移,如果上述转移成立,那么在第i-1行为k的情况下,我是可以放j的,也就是满足限制b。注意这里是加,不是乘。
第三个阶段写代码
(1)dp数组的初始化。最初的状态是只有一行,那么不受列的约束,所有的合法行都是可以的,那么dp[1][i]=1dp[1][i]=1dp[1][i]=1。
(2)递推dp数组。
a.第一层for循环表示的是规模 i表示当前考虑了前i行 1:n
b.第二层for循环表示的是限制 j表示所有可能出现的行 0:(1<<n)-1
判断行是否合法,即限制a和限制b
c.第三层for循环表示的是dp数组的转移点 即第i-1行所有的状态k 0:(1<<n)-1
这里要判断一下j和k是否冲突即限制b
(3)表示答案。res+=dp[n][j(所有的合法行)]res+=dp[n][j(所有的合法行)]res+=dp[n][j(所有的合法行)]
题目代码
import java.util.Scanner;
public class Main{
public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = scanner.nextInt();long dp[][] = new long[n+1][1<<n];int map[] = new int[n+1];for(int i = 1;i <= n;i++)for(int j = 0;j < n;j++) {int u = scanner.nextInt();if(u==1) map[i] |= (1<<j);}int mod = (int) 1e8;boolean book[] = new boolean[1<<n];for(int i = 0;i < (1<<n);i++) book[i]=(i&(i<<1))==0;for(int i = 0;i < (1<<n);i++) {if(book[i]&&(map[1]&i)==i)dp[1][i]=1;}for(int i = 2;i <= n;i++) {for(int j = 0;j < (1<<n);j++) {if((map[i]&j)==j&&book[j]) {for(int k = 0;k < (1<<n);k++) {if((k&j)==0) dp[i][j] = (dp[i][j]+dp[i-1][k])%mod;}}}}long res = 0;for(int i = 0;i < (1<<n);i++) res = (res+dp[n][i])%mod;System.out.println(res);
}
}
