Java数据结构第二十五期：红黑树传奇，当二叉树穿上 “红黑铠甲” 应对失衡挑战

专栏：Java数据结构秘籍

个人主页：手握风云

目录

一、红黑树

1.1. 概念

1.2. 性质

1.3. 节点的定义

1.4. 红黑树的插入

1.5. 红黑树的验证

1.6. AVL树和红黑树的比较

1.7. 红黑树的应用

---

一、红黑树

1.1. 概念

         红黑树（Red-Black Tree）是一种自平衡二叉查找树。它在普通的二叉查找树的基础上，为每个节点增加了颜色属性（红色或黑色），并通过对任何 一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

1.2. 性质

• 树的根节点必须是黑色的。
• 每个节点要么是红色，要么是黑色。
• 最长路径最多是最短路径的两倍
• 如果一个节点是红色，那么它的两个子节点必须都是黑色的。
• 所有的叶子节点都是黑色的。
• 从任意一个节点到其后代叶子节点的所有简单路径上，包含的黑色节点数量必须相同。

        假设一棵红黑树总共有n个节点，其中有x个黑色节点，那么n的范围是[x, 2x]。

1.3. 节点的定义

public class RBTree {// 节点定义static class RBTreeNode {public RBTree left;public RBTree right;public RBTree parent;public int val;public COLOR color;public RBTreeNode(int val) {this.val = val;this.color = COLOR.RED;}}public RBTreeNode root;
}

// 定义一个枚举类，表示颜色
public enum COLOR {// 定义两个枚举常量，表示红色和黑色RED, BLACK;
}

        新增的节点默认是红色的，如果默认是黑色的，根据红黑树的性质，每个叶子节点必须是黑色的，那我们就需要新增黑色节点来保持平衡。如果默认是红色的，我们进需要调节节点颜色来保持红黑树的性质。

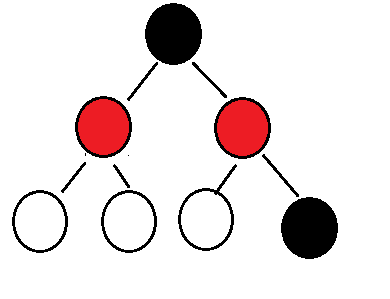
1.4. 红黑树的插入

        红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此我们可以先按照二叉搜索树的插入规则来插入，再检查红黑树的性质是否遭到破坏。

/*** 插入* @param val* @return*/
public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;root.color = COLOR.BLACK;return true;}RBTreeNode parent = null;RBTreeNode cur = root;while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val == val) {return false;} else {parent = cur;cur = cur.left;}}// 此时cur引用为空if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;
}

        因为新插入的节点默认为红色，如果它的父亲节点为黑色，符合红黑树的性质，不需要调整。但如果它的父亲节点为红色，则需要调整。

• cur为红，p为红，g为黑，u存在且为红。

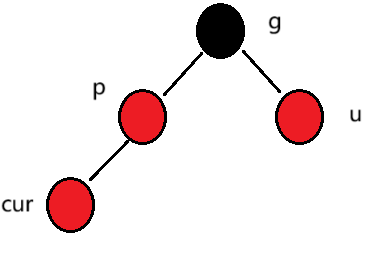
        此时如果只修改p为黑，不满足每条路径上有相同的黑色节点，必须把p和u全部修改为黑色节点。但如果上面这棵树是某棵树的子树，g的父亲节点也有可能是红色或者黑色。

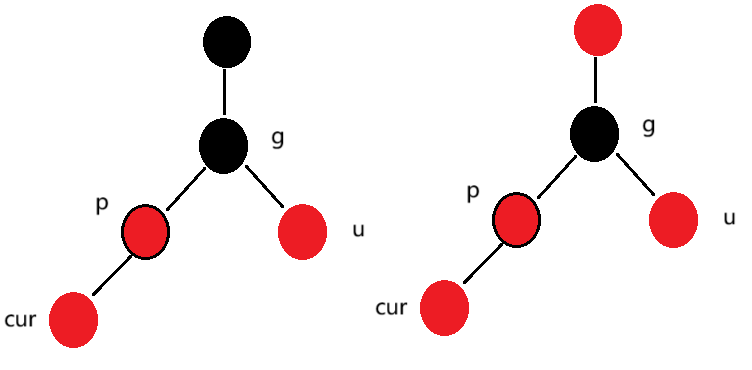
        如果节点g的父亲节点为黑色，那么它的兄弟节点也必须为黑色，只是单纯将p和u修改为黑色，就会增加黑色节点的数量，就需要再把g变为红色。所以解决完上述问题，我们都要把g手动调整为红色。那如果g的父亲节点为红色，那这棵树依然是子树，就继续按照这个规则向上调整。

while (parent != null && parent.color == COLOR.RED) {RBTreeNode grandFather = parent.parent;if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandFather.color = COLOR.RED;cur = grandFather;parent = cur.parent;}}
}

• cur为红，p为红，g为黑，u不存在或者u为黑

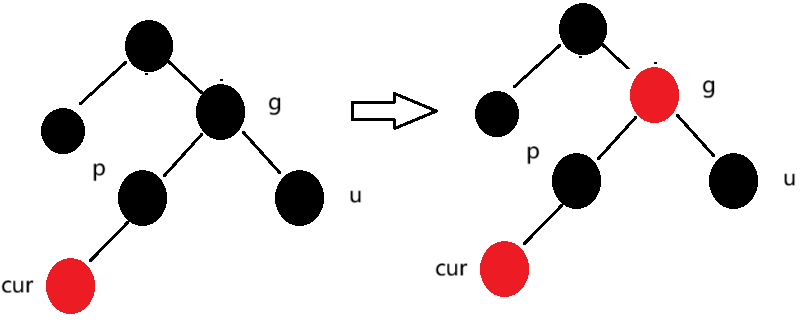
        如果u节点不存在，则cur一定是新插入的节点，因为如果cur不是新插入节点，则cur和p一定有一个节点颜色为黑色，就不满足每条路径上黑色节点数目相同。如果u节点存在，则一定是黑色的，那么cur节点原来的颜色一定是黑色的，在调整的过程中cur由黑色变为红色。

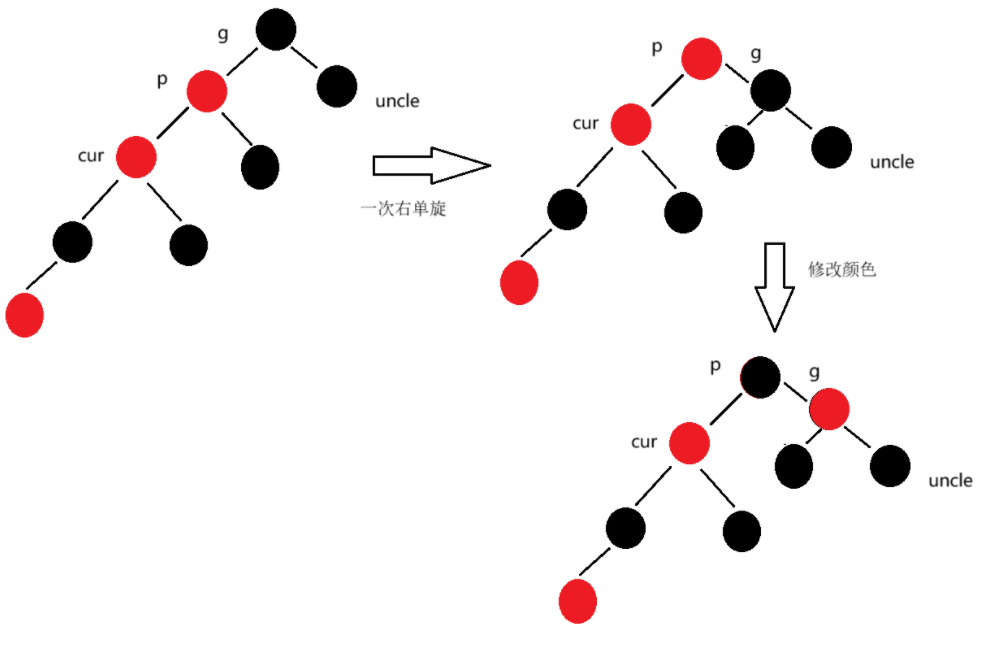
        此时，我们需要进行一次右单旋，将p的右孩子引用指向g，再将p修改为红色，g修改为黑色。

else {// uncle节点为空 或者 uncle节点为黑色RotateRight(grandFather);grandFather.color = COLOR.RED;parent.color = COLOR.BLACK;
}

/*** 右单旋* @param parent*/
private void RotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;parent.left = subLR;subLR.right = parent;if (subLR != null) {subLR.parent = parent;}RBTreeNode parent1 = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent1.left == parent) {parent1.left = subL;} else if (parent1.right == parent) {parent.right = subL;}subL.parent = parent1;}
}

• cur为红，p为红，g为黑，u不存在或者u为黑色

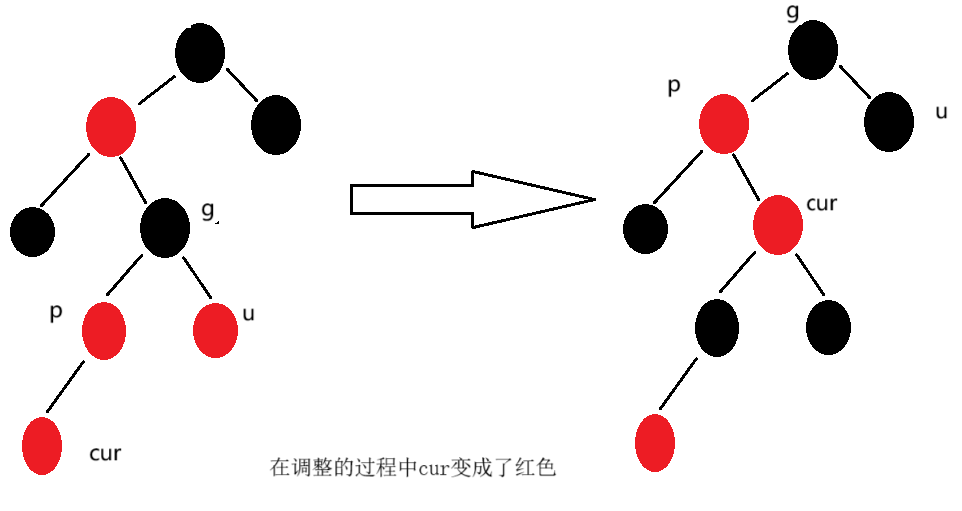
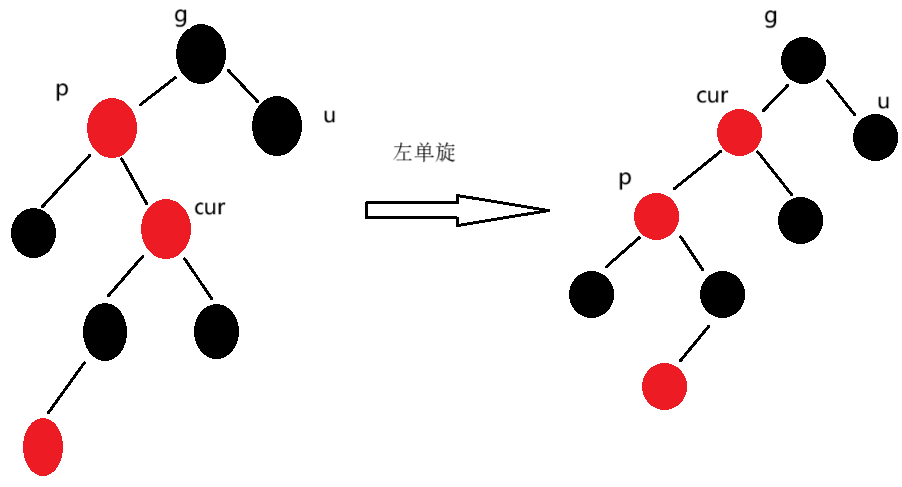
        我们会发现，当p为g的左孩子节点，cur为p的右孩子节点时，针对p进行左单旋操作，旋转之后，结构就与第二种情况相似了，只不过cur与p的引用不一样。

if (cur == parent.left) {RotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;
}
// uncle节点为空 或者 uncle节点为黑色
RotateRight(grandFather);
grandFather.color = COLOR.RED;
parent.color = COLOR.BLACK;

        当p为g的左孩子结点时，只需要改变针对p先进行右旋，再进行左旋，其他不需要变。

/*** 插入* @param val* @return*/
public boolean insert(int val) {RBTreeNode node = new RBTreeNode(val);if (root == null) {root = node;return true;}RBTreeNode parent = null;RBTreeNode cur = root;while (cur != null) {if (cur.val < val) {parent = cur;cur = cur.right;} else if (cur.val == val) {return false;} else {parent = cur;cur = cur.left;}}// 此时cur引用为空if (parent.val < val) {parent.right = node;} else {parent.left = node;}node.parent = parent;cur = node;// 调整颜色while (parent != null && parent.color == COLOR.RED) {RBTreeNode grandFather = parent.parent;if (parent == grandFather.left) {RBTreeNode uncle = grandFather.right;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandFather.color = COLOR.RED;cur = grandFather;parent = cur.parent;} else {if (cur == parent.left) {RotateLeft(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// uncle节点为空 或者 uncle节点为黑色RotateRight(grandFather);grandFather.color = COLOR.RED;parent.color = COLOR.BLACK;}} else {// p为g的右孩子节点RBTreeNode uncle = grandFather.left;if (uncle != null && uncle.color == COLOR.RED) {parent.color = COLOR.BLACK;uncle.color = COLOR.BLACK;grandFather.color = COLOR.RED;cur = grandFather;parent = cur.parent;} else {if (cur == parent.left) {RotateRight(parent);RBTreeNode tmp = parent;parent = cur;cur = tmp;}// uncle节点为空 或者 uncle节点为黑色RotateLeft(grandFather);grandFather.color = COLOR.RED;parent.color = COLOR.BLACK;}}}return true;
}/*** 左单旋* @param parent*/
private void RotateLeft(RBTreeNode parent) {RBTreeNode subR = parent.right;RBTreeNode subRL = subR.left;parent.right = subRL;subR.left = parent;if (subRL != null) {subRL.parent = parent;}RBTreeNode parent1 = parent.parent;parent.parent = subR;if (root == parent) {root = subR;root.parent = null;} else {if (parent1.left == parent) {parent1.left = subR;} else if (parent1.right == parent) {parent1.right = subR;}subR.parent = parent1;}
}/*** 右单旋* @param parent*/
private void RotateRight(RBTreeNode parent) {RBTreeNode subL = parent.left;RBTreeNode subLR = subL.right;parent.left = subLR;subL.right = parent;if (subLR != null) {subLR.parent = parent;}RBTreeNode parent1 = parent.parent;parent.parent = subL;if (parent == root) {root = subL;root.parent = null;} else {if (parent1.left == parent) {parent1.left = subL;} else if (parent1.right == parent) {parent1.right = subL;}subL.parent = parent1;}
}

1.5. 红黑树的验证

        红黑树的验证分为两个部分：1.先检查中序遍历结果是否有序；2.验证是否符合红黑树的性质。我们先判断是否存在两个连在一起的红色节点，先对红黑树进行递归遍历，当遍历到某个节点为红色时，则判断其父亲节点的颜色。

public boolean checkRedColor(RBTreeNode root) {if (root == null) {return true;}// 如果根节点的颜色为红色，则检查其父节点的颜色if (root.color == COLOR.RED) {RBTreeNode parent = root.parent;// 如果父节点的颜色也为红色，则违反了红黑树的性质，返回falseif (parent.color == COLOR.RED) {System.out.println("违反性质：两个红色节点连在一起");return false;}}// 递归检查左子树和右子树return checkRedColor(root.left) && checkRedColor(root.right);
}

        当我们判断每条路径上的黑色节点是否相同时，从根节点进行递归遍历，当其颜色为黑色时，则++，同时还要保留遍历过的路径上的黑色节点。当其左右孩子都为空时，停止遍历。

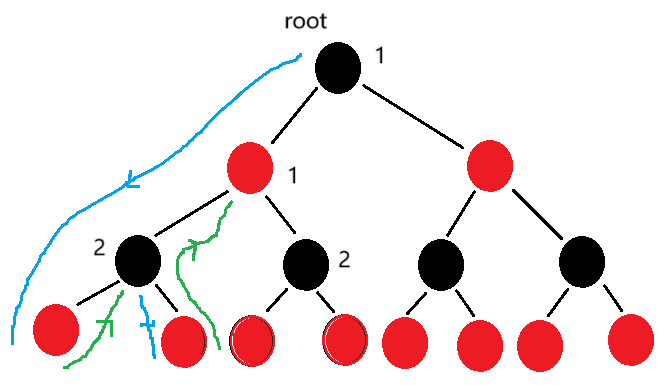
public boolean checkBlackNum(RBTreeNode root, int pathBlackNum, int blackNum) {if (root == null) {return true;}// 如果当前节点为黑色节点，则路径黑色节点数量加1if (root.color == COLOR.BLACK) {pathBlackNum++;}// 如果当前节点为叶子节点，则判断路径黑色节点数量是否等于给定的黑色节点数量if (root.left == null && root.right == null) {if (pathBlackNum != blackNum) {System.out.println("违反了性质：每条路径上的黑色节点数量不一样");return false;}}// 递归判断左子树和右子树return checkBlackNum(root.left, pathBlackNum, blackNum)&& checkBlackNum(root.right, pathBlackNum, blackNum);
}

1.6. AVL树和红黑树的比较

        AVL 树和红黑树都是自平衡二叉查找树，它们在插入和删除操作后自动调整以保持树的平衡，从而确保查找、插入和删除操作的平均时间复杂度为 O(logn)。尽管它们的目的相同，但在平衡机制、性能特点和实际应用中存在显著差异。

特性	AVL树	红黑树
平衡严格性	严格：平衡因子为-1,0,1	宽松：通过红黑性质保证近似平衡
高度	更小，更接近完全二叉树 (1.44logn)	稍大 (2logn)
查找性能	更优	稍逊于AVL树
实现复杂度	维护平衡因子和处理多种旋转情况更复杂	维护颜色属性和少量旋转规则相对简洁
插入/删除性能	通常需要更多旋转，开销更大	通常需要更少旋转和重新着色，开销较小
内存开销	每个节点需要存储平衡因子	每个节点需要存储一个颜色位

1.7. 红黑树的应用

• 编程语言与标准库实现

        C++中STL里面的std::map、std::multimap、std::set、std::multiset，Java集合框架里面的TreeSet和TreeSet。

• 数据库系统

        数据库管理系统（DBMS）通常使用 B-树或其变种（如 B+ 树）来构建磁盘上的索引。然而，在内存数据库或需要频繁更新的内存索引中，红黑树可以提供更快的插入和删除性能，因为它们不需要像 B-树那样进行大量的磁盘 I/O。

• 文件系统

        Linux 内核在文件系统中使用了红黑树来管理文件描述符、目录项以及其他与文件操作相关的数据结构，确保了文件访问的高效性。