当前位置：首页 > news >正文

传染病传播模拟：基于社会接触网络的疫情预测模型

news 来源：原创 2025/6/14 13:08:30

在公共卫生领域，预测传染病的传播趋势对制定防控策略至关重要。本文将展示一个基于 R 语言的传染病传播模拟模型，该模型通过构建真实的社会接触网络，模拟疾病在不同年龄群体间的传播动态。

一、模型设计背景与核心参数 🔍

这个模拟模型基于瑞典人口结构和社会接触模式，考虑了家庭、托儿所、学校和其他社交接触四种传播场景。模型的核心参数包括：

# 传播率设置
transmission.households <- 0.07      # 家庭内部传播率
transmission.DCCs <- 0.04            # 托儿所传播率
transmission.school.classes <- 0.03  # 学校班级传播率
transmission.other.contacts <- 0.04  # 其他社交接触传播率# 年龄偏倚参数
age.bias.1 <- 1
age.bias.1to6 <- 0.33
age.bias.7to65 <- 0.18
age.bias.65 <- 0.3# 人口与社交结构参数
prop.children.attending.DCCs <- 0.79  # 上托儿所的儿童比例
average.group.size.DCC <- 16.7        # 托儿所平均规模
average.class.size.school <- 22       # 学校班级平均规模
probability.of.other.contacts <- 0.5  # 发生其他社交接触的概率

这些参数反映了不同场景下疾病传播的可能性，以及不同年龄段人群的易感性差异。家庭内部传播率最高，可能是因为密切接触和共同生活环境；而学校班级传播率相对较低，可能与通风条件和社交距离措施有关。

二、人口结构与社交网络构建 🧑👩👧👦

模型首先根据瑞典人口金字塔数据生成模拟人群，然后构建四种关键的社交网络：

# 基于瑞典人口金字塔生成年龄分布
sweden.pop.props <- c(2.9,2.9,2.7,2.4,3.4,3.4,3.1,3,3.1,3.5,3.1,2.9,2.7,3.2,2.6,1.9,1.4,1,0.6,0.1,0)
names(sweden.pop.props) <- c(seq(0,100,5)[-1], "100+")
pop.ages <- as.numeric(sample(names(sweden.pop.props), pop.size, replace = TRUE, prob = sweden.pop.props))# 构建家庭网络
fam.id <- 1
while(sum(is.na(family.membership[pop.ages<=20]))>0){n.children <- sample(as.numeric(names(num.siblings.props)), 1, prob=num.siblings.props) + 1child.index <- which((pop.ages<=20) & is.na(family.membership))[1:n.children]n.parents <- sample(c(1,2), 1, prob = c(prop.single.parent, 1-prop.single.parent))parent.index <- which((pop.ages>20) & (pop.ages<=50) & is.na(family.membership))[1:n.parents]family.membership[c(child.index, parent.index)] <- fam.idfam.id <- fam.id + 1
}# 构建托儿所和学校网络
# ... [代码省略]

这个过程模拟了真实社会中的家庭结构（包括单亲和双亲家庭）、儿童入托率和学校班级规模。特别巧妙的是，模型确保家庭成员在同一托儿所或学校班级，这反映了现实中的社交网络特点。

三、传播矩阵构建：量化接触风险 📊

模型的核心是构建一个传播矩阵，用于表示任意两个人之间的疾病传播概率：

transition.matrix <- matrix(1, nrow = pop.size, ncol = pop.size)# 家庭传播风险
for(f in unique(family.membership[!is.na(family.membership)])){index <- which(family.membership==f)transition.matrix[t(combn(index, 2))] <- transition.matrix[t(combn(index, 2))] * (1 - transmission.households)
}# 托儿所、学校和其他社交接触传播风险
# ... [代码省略]

这个矩阵的构建非常精妙。通过逐步应用不同场景的传播率，模型综合考虑了各种接触方式带来的风险。例如，如果两个人既是家庭成员，又在同一学校班级，他们之间的传播风险将同时受到这两种场景的影响。

四、疾病传播模拟与结果分析 📈

模型使用蒙特卡洛方法模拟疾病在人群中的传播过程：

# 初始化疫情状态
status.vector <- rep(0, pop.size)
remaining.carriage <- rep(0, pop.size)
index <- sample(pop.size, n.initial.carriers)
status.vector[index] <- 1
remaining.carriage[index] <- rpois(n = n.initial.carriers, lambda = 4)# 主模拟循环
for(t in 1:stop.time){# 计算感染概率prob.infection <- 1-exp(rowSums(log((1-status.vector) * transition.matrix)))prob.infection <- prob.infection*bias.probsis.infected <- runif(pop.size)<prob.infection# 更新感染状态和恢复期n.new.infections <- sum((status.vector<=0) & is.infected)remaining.carriage[(status.vector<=0) & is.infected] <- rpois(n = n.new.infections, lambda = 4) + 1status.vector <- is.infectedremaining.carriage <- remaining.carriage-1remaining.carriage[remaining.carriage<0] <- 0status.vector[remaining.carriage<=0] <- 0# 记录结果n.infected.vector[[t]] <- sum(status.vector)n.infected.age.matrix[t,] <- table(pop.ages.factor[status.vector==1])
}

这个模拟过程考虑了感染概率、潜伏期和恢复期，使模型更贴近真实疫情发展。每次迭代中，模型计算每个人的感染概率，随机决定是否感染，并更新他们的感染状态和恢复期。

五、结果可视化与分析 📊

最后，模型通过 ggplot2 绘制了两组关键图表：

# 总感染人数随时间变化
ggplot(plot.df, aes(x=time, y=total.infected)) +geom_line() + xlab("time (weeks)") + ylab("total infected")# 不同年龄组感染人数随时间变化
ggplot(plot.df, aes(x=time, y=`number infected`, col=age.group)) + geom_line() + xlab("time (weeks)") + ylab("total infected")

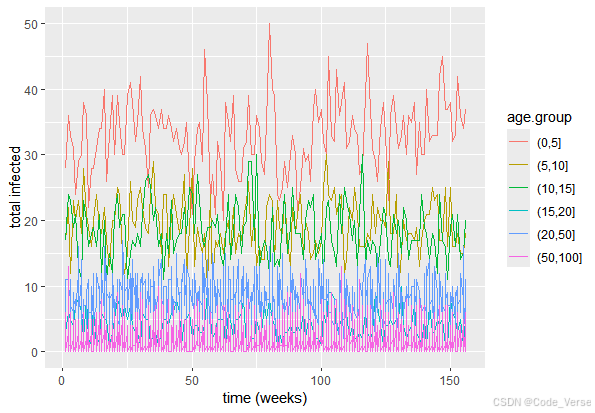
这些图表直观地展示了疫情发展趋势和年龄分布特征。通过分析这些图表，我们可以得出以下洞察：

传播曲线特征：总感染人数曲线呈现典型的传染病传播特征，包括潜伏期、爆发期和消退期。这与真实疫情数据的模式相符。
年龄差异分析：不同年龄组的感染曲线差异明显，这反映了模型中设置的年龄偏倚参数的影响。例如，儿童和老年人的感染曲线可能与其他年龄段有所不同。
社会接触网络影响：通过调整不同场景的传播率，我们可以模拟不同防控措施的效果。例如，关闭学校会降低学校班级传播率，从而影响整体疫情发展。

六、模型的应用价值与局限性 🌟

这个模型具有以下应用价值：

政策评估：可以模拟不同防控措施（如关闭学校、限制社交接触）对疫情传播的影响，为政策制定提供参考。
资源规划：预测不同阶段的感染人数，帮助医疗机构规划资源分配。
风险评估：识别高风险人群和传播场景，有针对性地采取防控措施。

然而，模型也存在一些局限性：

简化假设：模型对社交网络和传播机制做了一定简化，可能无法完全捕捉真实世界的复杂性。
参数不确定性：传播率和年龄偏倚等参数基于假设，可能与实际情况存在偏差。
未考虑行为变化：模型没有考虑疫情期间人们行为的动态变化，如自我隔离或加强防护措施。

七、结语与展望 🌍

通过这个模拟模型，我们可以更深入地理解传染病在社会网络中的传播机制，为疫情防控提供科学依据。未来，我们可以通过以下方式进一步改进模型：

引入更复杂的社交网络结构，如工作场所、公共场所等。
结合真实疫情数据，校准模型参数，提高预测准确性。
考虑疫苗接种、抗病毒药物等干预措施的效果。

传染病模拟是公共卫生领域的重要工具，它能帮助我们在疫情爆发前做好准备，在疫情期间做出科学决策。这个模型虽然简单，但展示了如何利用数学和计算方法来理解和应对复杂的公共卫生挑战。

希望这篇博客能帮助你理解传染病传播模拟的基本原理和方法，也欢迎你在评论区分享你的想法和建议！ 👇

这篇博客通过详细剖析代码逻辑，展示了传染病传播模拟的核心原理。如果你觉得某些部分需要更深入的解释，或者希望增加更多背景知识，可以随时告诉我。

完整代码（省流版）

library(ggplot2)
library(data.table)#transmission rates
transmission.households <- 0.07
transmission.DCCs <- 0.04
transmission.school.classes <- 0.03
transmission.other.contacts <- 0.04#age bias
age.bias.1 <- 1
age.bias.1to6 <- 0.33
age.bias.7to65 <- 0.18
age.bias.65 <- 0.3prop.children.attending.DCCs <- 0.79
average.group.size.DCC <- 16.7
average.class.size.school <- 22
probability.of.other.contacts <- 0.5pop.size <- 5000
n.initial.carriers <- 125
stop.time <- 156#sweden population pyramid
sweden.pop.props <- c(2.9,2.9,2.7,2.4,3.4,3.4,3.1,3,3.1,3.5,3.1,2.9,2.7,3.2,2.6,1.9,1.4,1,0.6,0.1,0)
names(sweden.pop.props) <- c(seq(0,100,5)[-1], "100+")#sweden family size proportions
num.siblings.props <- c(0.19,0.48,0.23,0.10)
names(num.siblings.props) <- c(0,1,2,3)
prop.single.parent <- 0.19pop.ages <- as.numeric(sample(names(sweden.pop.props), pop.size, replace = TRUE, prob = sweden.pop.props))
family.membership <- rep(NA, pop.size)
school.membership <- rep(NA, pop.size)
dcc.membership <- rep(NA, pop.size)
other.close.contact.pair <- rep(NA, pop.size)#randomly assign an individual a close contact with probability 0.5.
npairs <- rbinom(1, pop.size, 0.5)
pairs <- matrix(sample(pop.size, 2*npairs, replace = TRUE), ncol=2)#assign families
fam.id <- 1
while(sum(is.na(family.membership[pop.ages<=20]))>0){ #we still have un-assigned childrenn.children <- sample(as.numeric(names(num.siblings.props)), 1, prob=num.siblings.props) + 1child.index <- which((pop.ages<=20) & is.na(family.membership))[1:n.children]n.parents <- sample(c(1,2), 1, prob = c(prop.single.parent, 1-prop.single.parent))parent.index <- which((pop.ages>20) & (pop.ages<=50) & is.na(family.membership))[1:n.parents]family.membership[c(child.index, parent.index)] <- fam.idfam.id <- fam.id + 1
}#assign dcc
dcc.id <- 1
n.under.5 <- sum(pop.ages<=5)
indexs.in.dcc <- sample(which(pop.ages<=5), size = floor(prop.children.attending.DCCs*n.under.5))
family.ids <-  unique(family.membership[indexs.in.dcc])
dcc.size <- 0
for(f in family.ids){index <- indexs.in.dcc[family.membership[indexs.in.dcc]==f]dcc.membership[index] <- dcc.iddcc.size <- dcc.size + length(index)if(dcc.size>average.group.size.DCC){dcc.size <- 0dcc.id <- dcc.id + 1}
}#assign schools
#5 to 10
class.id <- 1
indexes.in.school <- which((pop.ages>5) & (pop.ages<=10))
family.ids <-  unique(family.membership[indexes.in.school])
class.size <- 0
for(f in family.ids){index <- indexes.in.school[family.membership[indexes.in.school]==f]school.membership[index] <- class.idclass.size <- class.size + length(index)if(class.size>average.class.size.school){class.size <- 0class.id <- class.id + 1}
}#10 to 15yrs
indexes.in.school <- which((pop.ages>10) & (pop.ages<=15))
family.ids <-  unique(family.membership[indexes.in.school])
class.size <- 0
for(f in family.ids){index <- indexes.in.school[family.membership[indexes.in.school]==f]school.membership[index] <- class.idclass.size <- class.size + length(index)if(class.size>average.class.size.school){class.size <- 0class.id <- class.id + 1}
}transition.matrix <- matrix(1, nrow = pop.size, ncol = pop.size)
#household transmission
for(f in unique(family.membership[!is.na(family.membership)])){index <- which(family.membership==f)transition.matrix[t(combn(index, 2))] <- transition.matrix[t(combn(index, 2))] * (1 - transmission.households)
}#dcc transmission
for(f in unique(dcc.membership[!is.na(dcc.membership)])){index <- which(dcc.membership==f)transition.matrix[t(combn(index, 2))] <- transition.matrix[t(combn(index, 2))] * (1 - transmission.DCCs)
}#school transmission
for(f in unique(school.membership[!is.na(school.membership)])){index <- which(school.membership==f)transition.matrix[t(combn(index, 2))] <- transition.matrix[t(combn(index, 2))] * (1 - transmission.school.classes)
}#other transmission
transition.matrix[pairs] <- transition.matrix[pairs] * (1 - transmission.other.contacts)
transition.matrix[pairs[,c(2,1)]] <- transition.matrix[pairs[,c(2,1)]] * (1 - transmission.other.contacts)#bias probability vector
bias.probs <- rep(NA, pop.size)
bias.probs[pop.ages<=5] <- 0.33
bias.probs[pop.ages>65] <- 0.3
bias.probs[is.na(bias.probs)] <- 0.18status.vector <- rep(0, pop.size)
remaining.carriage <- rep(0, pop.size)#initialise infections
index <- sample(pop.size, n.initial.carriers)
status.vector[index] <- 1
remaining.carriage[index] <- rpois(n = n.initial.carriers, lambda = 4)pop.ages.factor <- factor(pop.ages)
n.infected.vector <- rep(NA, stop.time)
n.infected.age.matrix <- matrix(NA, nrow = stop.time, ncol = length(unique(pop.ages.factor)))
colnames(n.infected.age.matrix) <- levels(pop.ages.factor)for(t in 1:stop.time){# message(paste("Time:", t))prob.infection <- 1-exp(rowSums(log((1-status.vector) * transition.matrix)))prob.infection <- prob.infection*bias.probsis.infected <- runif(pop.size)<prob.infectionn.new.infections <- sum((status.vector<=0) & is.infected)remaining.carriage[(status.vector<=0) & is.infected] <- rpois(n = n.new.infections, lambda = 4) + 1status.vector <- is.infectedremaining.carriage <- remaining.carriage-1remaining.carriage[remaining.carriage<0] <- 0status.vector[remaining.carriage<=0] <- 0n.infected.vector[[t]] <- sum(status.vector)n.infected.age.matrix[t,] <- table(pop.ages.factor[status.vector==1])}plot.df <- data.frame(time=1:stop.time, total.infected=n.infected.vector, stringsAsFactors = FALSE)ggplot(plot.df, aes(x=time, y=total.infected)) +geom_line() + xlab("time (weeks)") + ylab("total infected")plot.df <- reshape2::melt(n.infected.age.matrix)
colnames(plot.df) <- c("time", "age.group", "number infected")
plot.df$age.group <- cut(plot.df$age.group, breaks = c(0,5,10,15,20,50,100))ggplot(plot.df, aes(x=time, y=`number infected`, col=age.group)) + geom_line() + xlab("time (weeks)") + ylab("total infected")table(cut(pop.ages, breaks = c(0,5,10,15,20,50,100)))