探索数学的迷人谜题:考兰兹猜想与MATLAB演示
探索数学的迷人谜题:考兰兹猜想与MATLAB演示
考兰兹猜想(Collatz Conjecture)又称"3n+1问题",是数学中最著名的未解之谜之一。这个看似简单的序列规则背后隐藏着深不可测的复杂性,吸引了无数数学家和爱好者的探索。
什么是考兰兹猜想?
考兰兹猜想由德国数学家洛塔尔·考兰兹于1937年提出,其规则极为简单:
- 从一个正整数n开始
- 如果n是偶数,则下一步变为n/2
- 如果n是奇数,则下一步变为3n+1
- 重复上述过程
猜想认为:无论起始数字是什么,这个序列最终都会进入4→2→1的循环。
数学意义与挑战
- 简单规则,复杂行为:序列变化看似随机,难以预测
- 未证明的猜想:尽管对所有小于2⁶⁸的数字都验证成立,但尚未有一般性证明
- 研究价值:涉及数论、动力系统、计算理论等多个数学领域
MATLAB演示与可视化
function collatz_demo(start_num)% 生成考兰兹序列sequence = start_num;while start_num ~= 1if mod(start_num, 2) == 0start_num = start_num / 2;elsestart_num = 3 * start_num + 1;endsequence(end+1) = start_num; %#ok<AGROW>end% 可视化结果figure('Position', [100, 100, 900, 500])% 序列图subplot(1,2,1)plot(sequence, 'o-', 'LineWidth', 1.5, 'MarkerFaceColor', [0.3, 0.6, 0.9])title(sprintf('起始值: %d (步数: %d)', sequence(1), length(sequence)-1))xlabel('步骤')ylabel('数值')grid onset(gca, 'YScale', 'log')% 路径分析图subplot(1,2,2)hold onfor i = 1:length(sequence)-1x = [i, i+1];y = [sequence(i), sequence(i+1)];if sequence(i) > sequence(i+1)plot(x, y, 'b-', 'LineWidth', 1.5) % 下降路径elseplot(x, y, 'r-', 'LineWidth', 1.5) % 上升路径endendtitle('序列变化路径')xlabel('步骤')ylabel('数值')legend('下降 (n/2)', '上升 (3n+1)', 'Location', 'best')grid onhold off
end
使用示例与结果分析
% 测试不同起始值
collatz_demo(6); % 短序列示例
collatz_demo(27); % 著名长序列示例
collatz_demo(871); % 复杂序列示例
典型序列特征:
- 瀑布式下降:连续除以2导致数值快速下降
- 奇数次跃升:3n+1操作使数值大幅上升
- 最终收敛:所有测试序列最终都到达1
6的运算结果

27的运算结果

871的运算结果
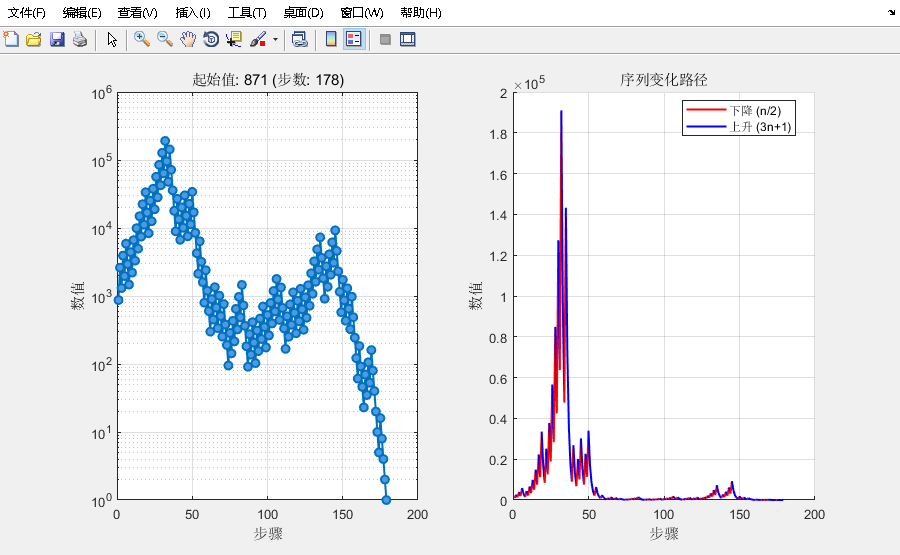
(示例图:左侧显示序列值变化,右侧用颜色区分上升/下降路径)
研究进展与计算挑战
- 验证记录:截至2023年,所有小于2⁶⁸ ≈ 2.95×10²⁰的数字均验证成立
- 计算瓶颈:序列长度无法预测,某些数需要数千步才收敛
- 概率模型:Terras定理证明几乎所有的起始值最终都会小于自身
为什么重要?
考兰兹猜想代表了数学中最迷人的一类问题:简单的规则产生不可预测的行为。它提醒我们,即使是最基本的算术运算,也可能隐藏着深奥的数学真理。
“数学不是关于答案,而是关于探索问题的过程。” —— Paul Erdős
您可以在MATLAB中尝试不同起始值,观察序列的独特行为。虽然我们可能无法解决这个百年难题,但每个人都可以参与这趟数学探索之旅!
