当前位置：首页 > news >正文

归并排序：分治思想的高效排序

news 来源：原创 2025/6/9 7:41:17

基本原理

流程图解

实现方法

递归实现

非递归实现

演示过程

时间复杂度

基本原理

归并排序(Merge Sort)是一种基于分治思想的排序算法，由约翰·冯·诺伊曼在1945年提出。其核心思想包括：

分割(Divide)：将待排序数组递归地分成两个子数组，直到每个子数组只包含一个元素（此时认为已排序）

合并(Merge)：将两个已排序的子数组合并成一个更大的有序数组

归并排序的关键在于"合并"操作，即如何将两个已排序的数组高效地合并成一个有序数组。这一过程通常使用额外的临时数组来存储合并结果。

流程图解

动图展示

分割图解和合并图解

动图展示

实现方法

递归实现

这是最直观的归并排序实现，使用递归方式：

//归并排序（子函数）
void _MergeSort(int* a, int left, int right, int* tmp)
{if (left >= right)//归并结束条件：当只有一个数据或是序列不存在时，不需要再分解{return;}int mid = left + (right - left) / 2;//中间下标_MergeSort(a, left, mid, tmp);//对左序列进行归并_MergeSort(a, mid + 1, right, tmp);//对右序列进行归并int begin1 = left, end1 = mid;int begin2 = mid + 1, end2 = right;//将两段子区间进行归并，归并结果放在tmp中int i = left;while (begin1 <= end1&&begin2 <= end2){//将较小的数据优先放入tmpif (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}//当遍历完其中一个区间，将另一个区间剩余的数据直接放到tmp的后面while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//归并完后，拷贝回原数组int j = 0;for (j = left; j <= right; j++)a[j] = tmp[j];
}
//归并排序（主体函数）
void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与原数组大小相同的空间if (tmp == NULL){printf("malloc fail\n");exit(-1);}_MergeSort(a, 0, n - 1, tmp);//归并排序free(tmp);//释放空间
}

非递归实现

gap 代表单个区间元素个数，也就是区间长度
一次归并排序两个长度为 gap 的区间
若想要排序下一组（即两个长度为 gap 的区间），就需要每轮的最后，一次跳过 2*gap 长度（代表跳过前面排序的两个长度为 gap 的区间）
gap 从1开始对两个有序数组进行排序，直到 gap >= n 时结束 ( n 为数组长度，这个就是外层while循环的结束条件 )

演示过程

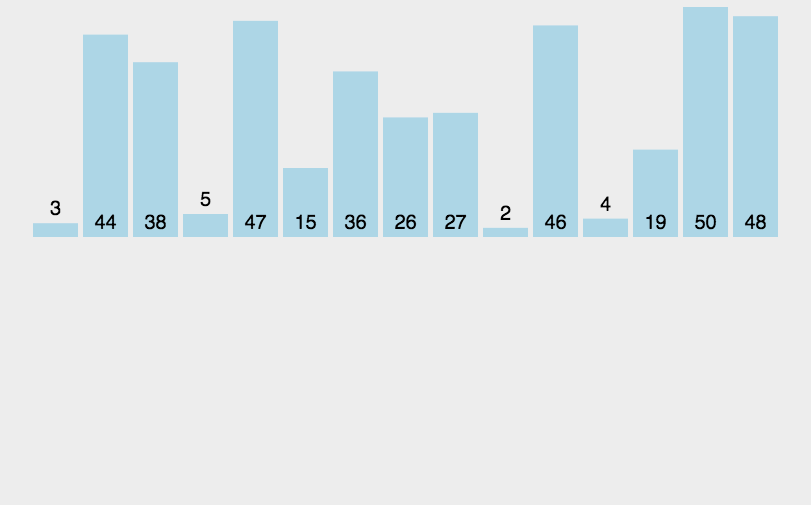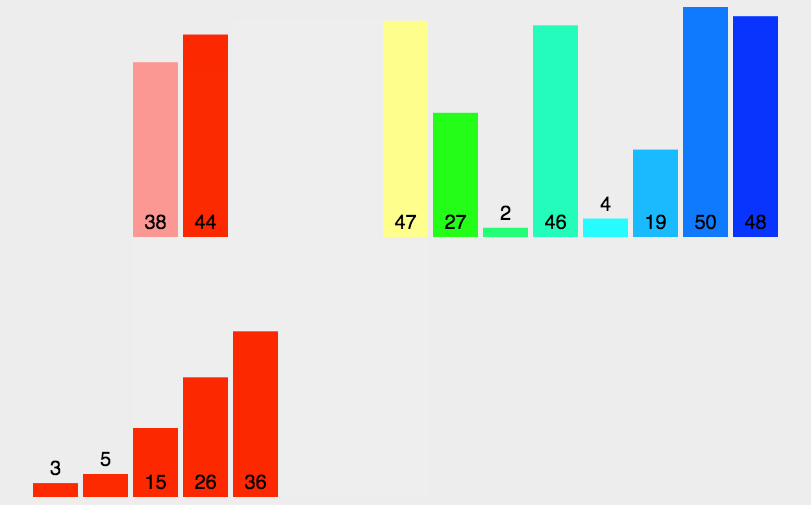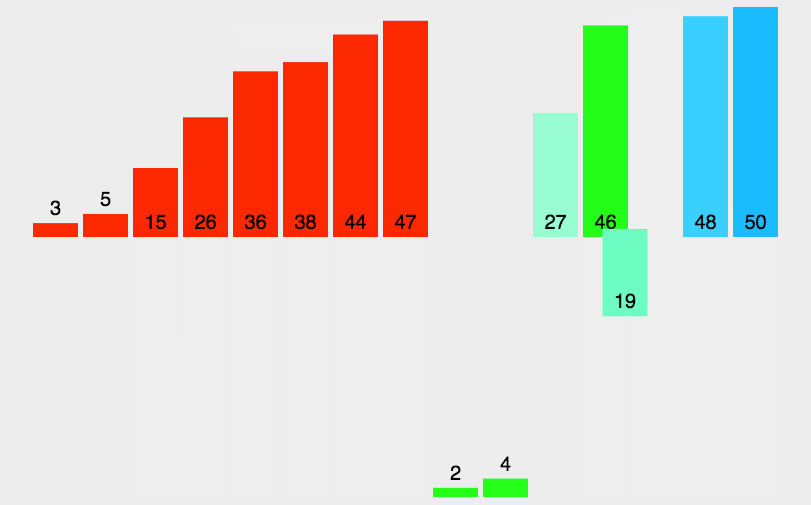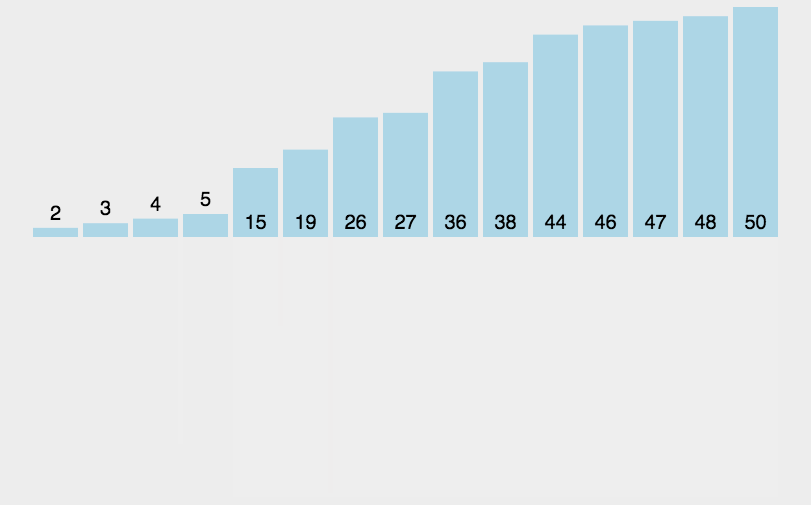
利用循环实现归并排序时，我们也可以 先将数组中每一个元素单独作为一组

第一轮 gap == 1 时：让 两两元素归并排序 为一个含有两个元素的有序数组，然后 gap *= 2（gap 变成了 2）

第二轮 gap == 2 时：让两个含有两个元素的有序数组归并为一个含有四个元素的有序数组，然后 gap *= 2（gap 变成了 4）

第三轮 gap == 3 时：然后再让两个含有四个元素的有序数组归并为一个含有八个元素的有序数组，然后 gap *= 2（gap 变成了 8）

就这样一直循环下去，直到 gap >= n ( n 为数组长度，这个就是外层while循环的结束条件 ) 时结束，结束时，数组就有序了

当然，以上例子是一个待排序列长度比较特殊的例子，我们若是想写出一个广泛适用的程序，必定需要考虑到某些极端情况：

第一种：第一个区间的 end1 越界

则这一小区间就无需执行本轮的归并排序了（不是以后都不归并，而是当前这一轮不用了），保留原数组数据即可（因为一个区间肯定保证是有序的）

第二种：第二个区间的begin2 越界

说明第二个区间也不存在，则这一小区间也无需执行本轮的归并排序了，保留原数组数据

第三种：第二个区间的 end2 越界

当 end2 越界，（这里也就说明前面几项都没越界），需要修正end2：end2 直接等于右边界 end2 = R （因为越界的一定是最后一组）

//归并排序（子函数）
void _MergeSortNonR(int* a, int* tmp, int begin1, int end1, int begin2, int end2)
{int j = begin1;//将两段子区间进行归并，归并结果放在tmp中int i = begin1;while (begin1 <= end1&&begin2 <= end2){//将较小的数据优先放入tmpif (a[begin1] < a[begin2])tmp[i++] = a[begin1++];elsetmp[i++] = a[begin2++];}//当遍历完其中一个区间，将另一个区间剩余的数据直接放到tmp的后面while (begin1 <= end1)tmp[i++] = a[begin1++];while (begin2 <= end2)tmp[i++] = a[begin2++];//归并完后，拷贝回原数组for (; j <= end2; j++)a[j] = tmp[j];
}
//归并排序（主体函数）
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);//申请一个与待排序列大小相同的空间，用于辅助合并序列if (tmp == NULL){printf("malloc fail\n");exit(-1);}int gap = 1;//需合并的子序列中元素的个数while (gap < n){int i = 0;for (i = 0; i < n; i += 2 * gap){int begin1 = i, end1 = i + gap - 1;int begin2 = i + gap, end2 = i + 2 * gap - 1;if (begin2 >= n)//最后一组的第二个小区间不存在或是第一个小区间不够gap个，此时不需要对该小组进行合并break;if (end2 >= n)//最后一组的第二个小区间不够gap个，则第二个小区间的后界变为数组的后界end2 = n - 1;_MergeSortNonR(a, tmp, begin1, end1, begin2, end2);//合并两个有序序列}gap = 2 * gap;//下一趟需合并的子序列中元素的个数翻倍}free(tmp);//释放空间
}