当前位置：首页 > news >正文

数据结构与算法——二叉树高频题目（2）

news 来源：原创 2025/6/9 6:20:15

前言：

继续记录关于二叉树高频题目的学习。学习二叉树有助于对于递归的应用和理解，为之后学习动态规划打好基础。题目主要围绕二叉树结构，结合递归求解。涉及二叉树的深度、二叉树层的宽度、二叉树的线性化、二叉树的序列化和反序列化、根据前中序遍历构建树、BFS（宽度优先遍历）。

参考视频：

算法讲解036【必备】二叉树高频题目-上-不含树型dp

题目解答：

⭐力扣--662.二叉树最大宽度

题目：

解题思路：

这题很容易想到使用层序遍历的模板有助于解题，关键在于如何处理空结点？

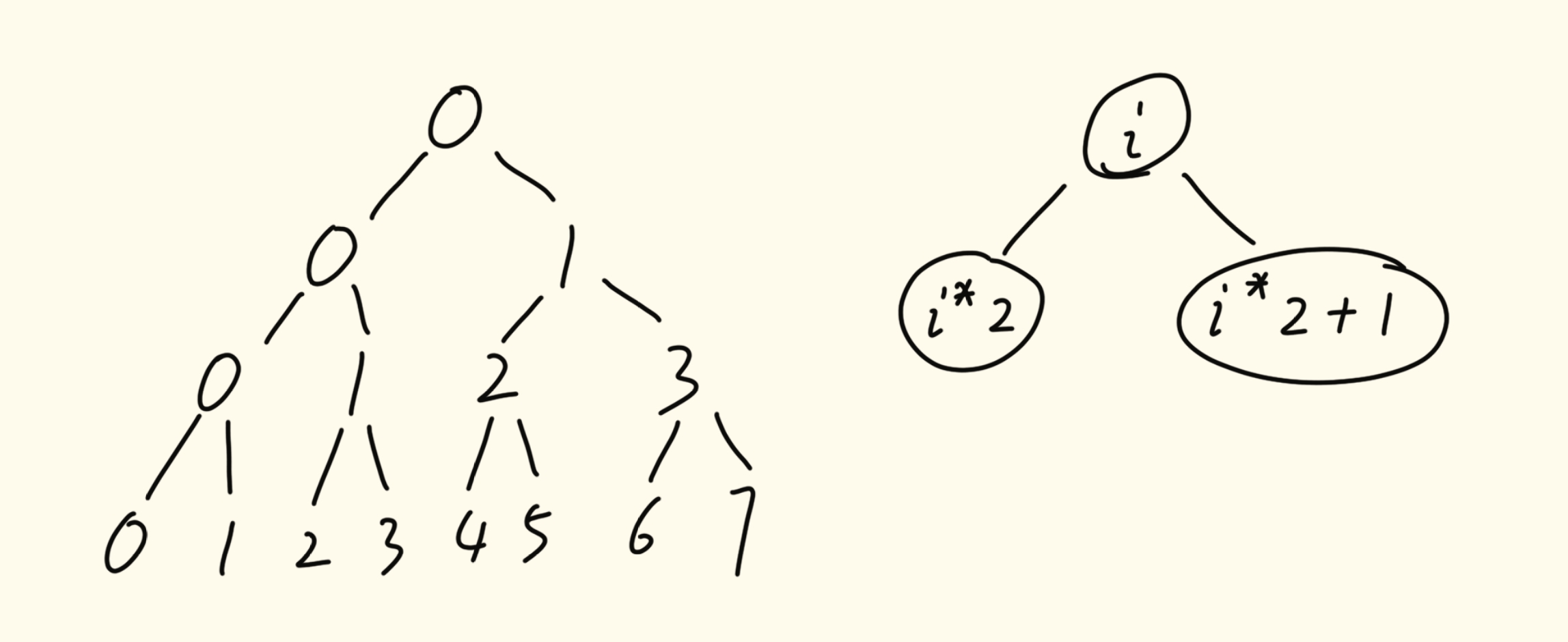
我们可以将二叉树进行线性化，以层编号所有结点，在使用队列层序遍历时，使用另一个相同结构记录结点线性化对应的编号。

至于树层的宽度，我们只需要层序遍历开始前，取队列的头尾结点对应的编号作差，即可得到符合题意的树层的宽度。

注意，由于二叉树可能深度很深，我们可以使用 unsigned long long 处理编号。

同时，由于编号只作额外信息，不作下标使用。所以可以使编号以 0 开始，每层的编号同样是以 0 开始。

示例代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:static constexpr int N = 3e3 + 1;vector<TreeNode*> queue;vector<unsigned long long> index;int size;
public:Solution() : queue(N), index(N) {}int widthOfBinaryTree(TreeNode* root) {unsigned long long ans = 0;if(root == nullptr){return ans;}queue[0] = root;index[0] = 0;size = 1;int l = 0, r = 1;//index 关系 //左孩子 i * 2 //右孩子 i * 2 + 1while(size != 0){int times = size;//当前层的宽度unsigned long long width = index[r - 1] - index[l] + 1;ans = max(ans, width);for(int i = 0; i < times; i++){TreeNode* cur = queue[l];unsigned long long cur_index = index[l];l++;size--;if(cur->left != nullptr){queue[r] = cur->left;index[r] = cur_index * 2;r++;size++;}if(cur->right != nullptr){queue[r] = cur->right;index[r] = cur_index * 2 + 1;r++;size++;}}}return ans;}
};

⭐力扣--104.二叉树的最大深度

题目：

解题思路：

主要重点在于递归的使用，通过对二叉树操作可有效帮助理解递归，这将有助于后续对于动态规划的学习。

树的高度 = max ( 左子树高度, 右子树高度 ) + 1

示例代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int maxDepth(TreeNode* root) {if(root == nullptr){return 0;}return 1 + max(maxDepth(root->left), maxDepth(root->right));}
};

⭐力扣--111二叉树的最小深度

题目：

解题思路：

本题只是在求二叉树最大深度问题上延申，很容易想到求左子树和右子树最小深度 + 1 即可。

但这里要注意，什么时候对左右子树进行调用递归？如果我们同求最大深度问题一样直接所有调递归，那将是错误的，因为空结点也会返回一个高度，这对于左右子树一空一非空的情况是不合适的。

所以我们对左右子树进行判断，如果左右有子树，才去递归求最小深度；如果左右有一个空子树，则不递归调用，同时用INT_MAX使数据无效；如果左右都没子树，则该结点为叶子结点，向上层返回 1 参与深度计算即可。

示例代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int minDepth(TreeNode* root) {if(root == nullptr){return 0;}if(root->left == nullptr && root->right == nullptr){return 1;}int lDeep = INT_MAX;int rDeep = INT_MAX;if(root->left){lDeep = minDepth(root->left);}if(root->right){rDeep = minDepth(root->right);}return min(lDeep, rDeep) + 1;}
};

⭐力扣--297.二叉树的序列化与反序列化

题目：

解题思路：

首先明确，为了使序列化结果与树结构一一对应，我们必须将空结点也视为信息，本题我们将以字符 '#' 代替空结点。同时会实现先序遍历版本和层序遍历版本。至于后序遍历，同先序遍历基本一致。而中序遍历无法做到序列化结果与树结构高度对应，示例如下。

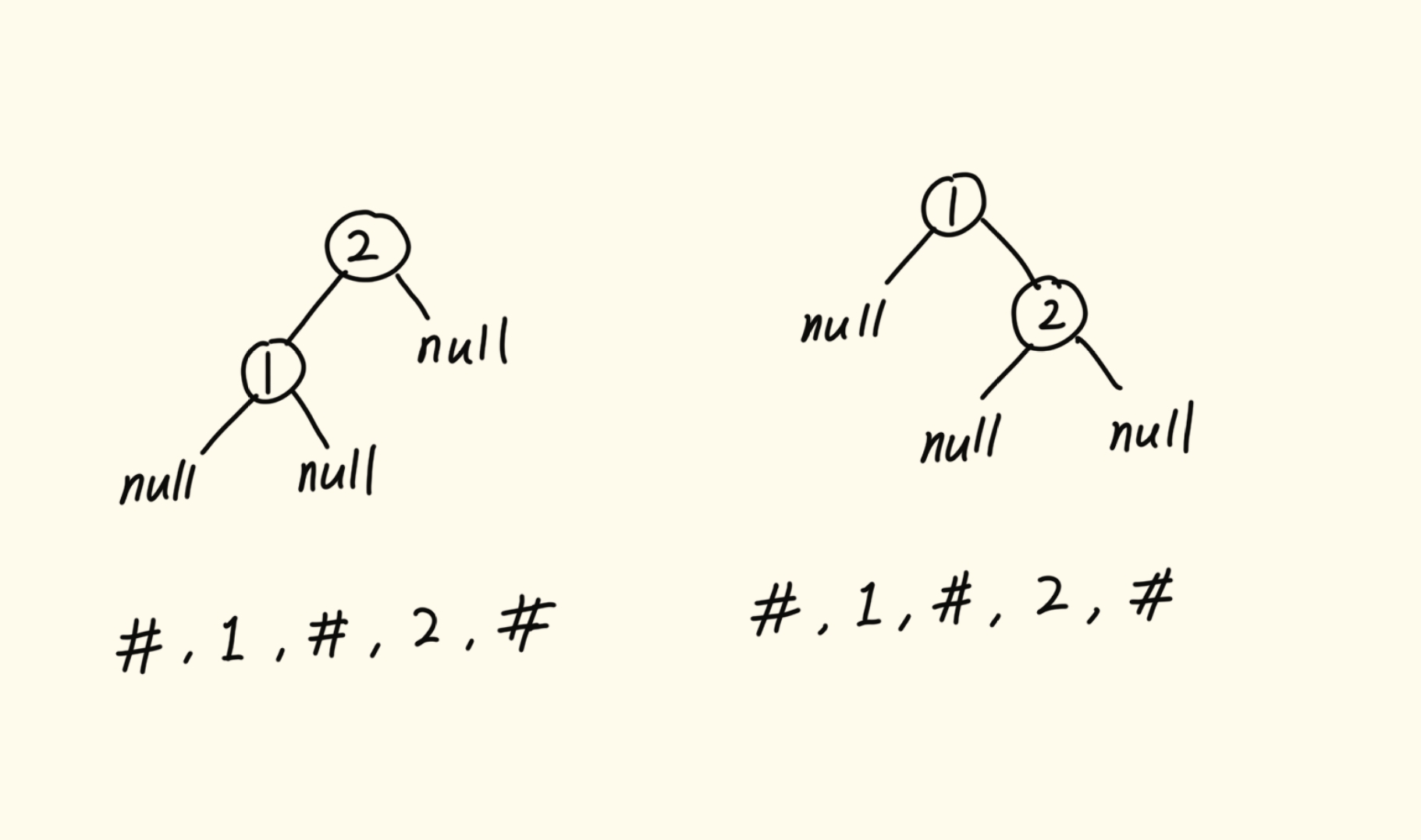
关于先序遍历：

序列化就按照先序遍历的代码，递归即可，空结点用 '#' 代替。

反序列化就将字符串信息分割，然后按先序顺序建树即可。值得注意的是 cnt ，建树时可以会有小伙伴下意识进行字符串信息for循环，但是这样如果递归的话，调用信息会乱。所以我们用全局（类内全局）变量 cnt 记录当前函数处理到的字符串位置。

关于层序遍历：

套用层序遍历模板即可，用字符 '#' 代替空结点，入队列时序列化即可。空结点时，结点序列化但不进队列。反序列化与序列化基本一致。

示例代码：

注：关于C++字符串分割和一些用到的api将在之后总结。

①先序遍历：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Codec {
private:int cnt;void mySerialize(TreeNode* root, string& s){if(root == nullptr){s += "#,";}else{s += to_string(root->val) + ",";mySerialize(root->left, s);mySerialize(root->right, s);}}TreeNode* myDeserialize(vector<string>& s){string cur = s[cnt++];if(cur == "#"){return nullptr;}else{int num = stoi(cur);TreeNode* cur_node = new TreeNode(num);cur_node->left = myDeserialize(s);cur_node->right = myDeserialize(s);return cur_node;}}vector<string> mySplit(const char delimiter, const string& s){vector<string> ans;stringstream ss(s);string item;while(getline(ss, item, delimiter)){if(!item.empty()){ans.push_back(item);}}return ans;}vector<string> split(const string& s, char delimiter) {vector<string> result;stringstream ss(s);string item;while (getline(ss, item, delimiter)) {if (!item.empty()) {  // 跳过空字符串result.push_back(item);}}return result;}
public:// Encodes a tree to a single string.string serialize(TreeNode* root) {//以'#'表示null结点string s;s.clear();mySerialize(root, s);return s;}// Decodes your encoded data to tree.TreeNode* deserialize(string data) {cnt = 0;vector<string> s = split(data, ',');TreeNode* root = myDeserialize(s);return root;}
};// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

②层序遍历：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/
class Codec {
private:static constexpr int N = 1e4 + 1;vector<TreeNode*> queue;vector<string> split(const char delimiter, const string& s){vector<string> ans;string item;stringstream ss(s);while(getline(ss, item, delimiter)){if(!item.empty()){ans.push_back(item);}}return ans;}
public:Codec() : queue(N) {}// Encodes a tree to a single string.string serialize(TreeNode* root) {string s;s.clear();if(root == nullptr){return s;}int l = 0, r = 1;queue[0] = root;s += to_string(root->val) + ",";while(l < r){TreeNode* cur = queue[l++];if(cur->left){queue[r++] = cur->left;s += to_string(cur->left->val) + ",";}else{s += "#,";}if(cur->right){queue[r++] = cur->right;s += to_string(cur->right->val) + ",";}else{s += "#,";}}return s;}// Decodes your encoded data to tree.TreeNode* deserialize(string data) {if(data == ""){return nullptr;}vector<string> s = split(',', data);int index = 1;int len = s.size();int l = 0, r = 0;TreeNode* root = new TreeNode(stoi(s[0]));queue[r++] = root;while(l < r){TreeNode* cur = queue[l++];cur->left = s[index] == "#" ? nullptr : new TreeNode(stoi(s[index])); index++;cur->right = s[index] == "#" ? nullptr : new TreeNode(stoi(s[index]));index++;if(cur->left){queue[r++] = cur->left;}if(cur->right){queue[r++] = cur->right;}}return root;}
};// Your Codec object will be instantiated and called as such:
// Codec ser, deser;
// TreeNode* ans = deser.deserialize(ser.serialize(root));

⭐力扣--105.从前序与中序遍历序列构造二叉树

题目：

解题思路：

根据树的前序遍历，我们可以确定根结点，接着由根结点在中序遍历的位置，我们可以知道根节点的左子树结点构成和右子树结点构成，那么我们只需要给定建树的两个范围：前序范围和中序范围，递归建树即可。

至于递归范围的确定，如图：

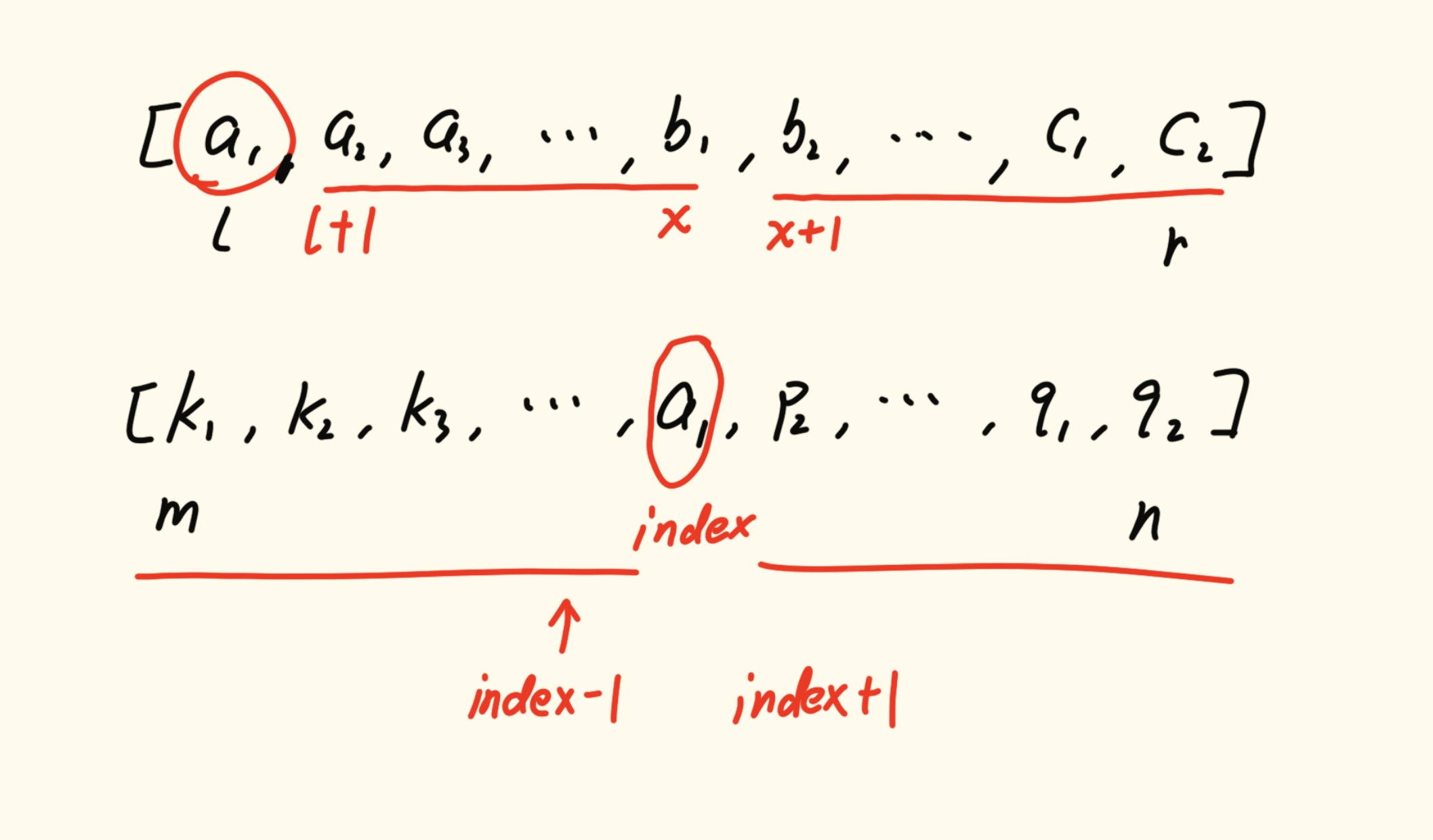
假设上方数组为前序遍历数组，下方数组为中序遍历数组。

我们每次递归都是以 l 位置建立根节点，接着找到 l 对应的值在中序遍历中的位置，记为 index 。

接着就是确定递归建立子树的范围。

如图，对于前序遍历，其左子树为 l + 1 ... x , 其右子树为 x + 1 ... r 。

对于中序遍历，其左子树为 m ... index - 1, 其右子树为 index + 1 ... n 。

最后求解x即可，由于树的长度确定，故：

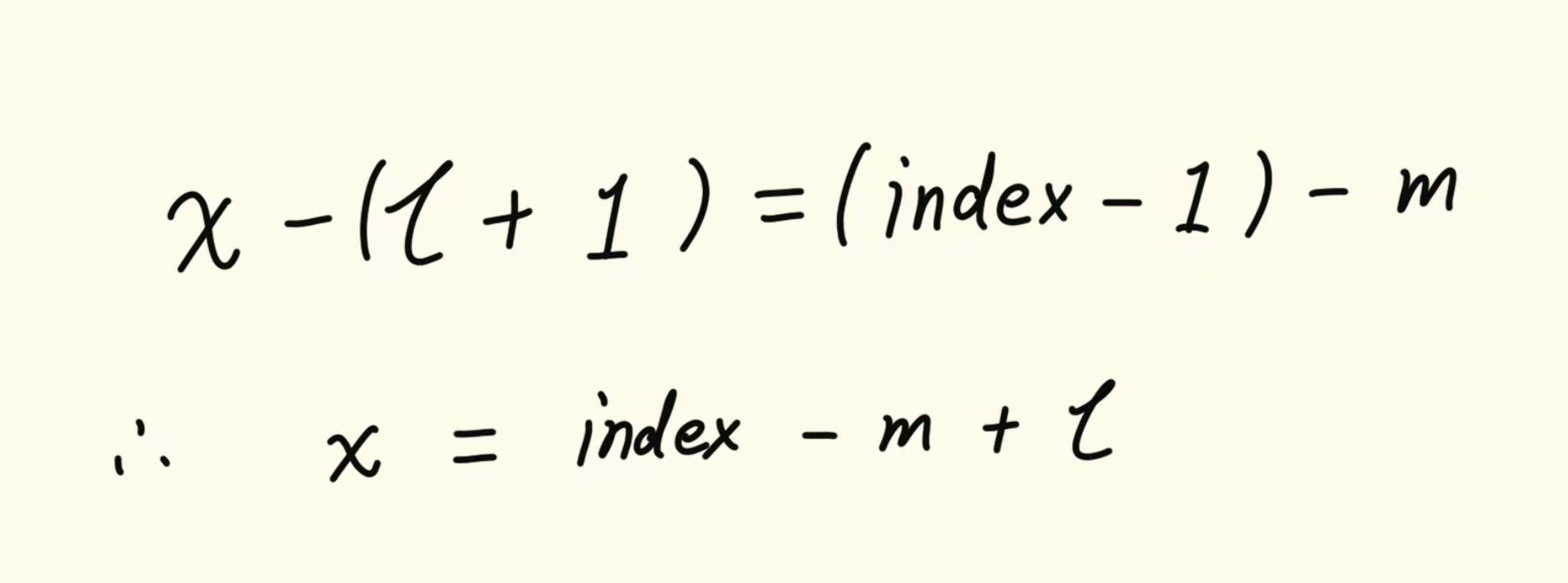
示例代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:unordered_map<int, int> map;//l...r 表示中序遍历数据范围//m...n 表示前序遍历数据范围TreeNode* buildTreeFunc(vector<int>& preorder, int l, int r, vector<int>& inorder, int m, int n){//不符合题意的即为叶子节点的空结点if(l > r || m > n){return nullptr;}//以 l 构建根结点TreeNode* root = new TreeNode(preorder[l]);//找到对应中序遍历中的下标int index = map[preorder[l]];//递归调用构建左子树和右子树root->left = buildTreeFunc(preorder, l + 1, index - m + l, inorder, m, index - 1);root->right = buildTreeFunc(preorder, index - m + l + 1, r, inorder, index + 1, n);return root;}//构建map，方便查找前序遍历的值在中序遍历数组中的下标void buildMap(vector<int>& inorder){map.clear();int n = inorder.size();for(int i = 0; i < n; ++i){map[inorder[i]] = i;}}
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {//构建mapbuildMap(inorder);//递归调用,格式：(先, l, r, 中, m, n);int r = preorder.size();int n = inorder.size();TreeNode* root = buildTreeFunc(preorder, 0, r - 1, inorder, 0, n - 1);return root;}
};

⭐力扣--958. 二叉树的完全性检验

题目：

解题思路：

由完全二叉树的性质，如果树高在两层以上，除最后两层外其余各层都是满的，所以该题与二叉树的层高度相关，所以我们可以考虑使用层序遍历。通过观察，如果按照层序遍历二叉树，当有树结点无左孩子但有右孩子时，其显然不是一颗完全二叉树。而当树节点第一次出现左右孩子不全的情况（无孩子或有左孩子无右孩子）时，之后层序遍历的结点都是叶子结点。根据这个性质，修改层序遍历代码，此题即迎刃而解。

示例代码：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:static constexpr int N = 100;vector<TreeNode*> queue;bool isLeavf;
public:Solution() : queue(N), isLeavf(false) {}bool isCompleteTree(TreeNode* root) {if(root->left == nullptr && root->right == nullptr){return true;}int l = 0, r = 0;queue[r++] = root;while(l < r){TreeNode* cur = queue[l++];//如果结点无左孩子但有右孩子，之间返回falseif(cur->left == nullptr && cur->right != nullptr){return false;}if(isLeavf){//如果应该是叶子结点，判断是否有孩子if(cur->left || cur->right){return false;}}else{//如果还没找到缺孩子情况，判断是否缺孩子if(!cur->left || !cur->right){isLeavf = true;}}if(cur->left){queue[r++] = cur->left;}if(cur->right){queue[r++] = cur->right;}}//如若循环完依然没有返回false, 则为完全二叉树return true;}
};

⭐力扣--完全二叉树的结点个数

题目：

解题思路：

首先我们可以想到层序遍历暴力求解。

接着我们思考如何优化，根据完全二叉树的性质和关于二叉树与递归高度关联，我们考虑递归。

通过观察：

当左子树的高度等于右子树高度时，左子树必为满二叉树。

当左子树的高度大于右子树高度时，右子树必为满二叉树。

而满二叉树的结点个数时可以通过高度之间求解的。

示例代码：

①层序遍历暴力求解：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:static constexpr int N = 5e4 + 1;vector<TreeNode*> queue;
public:Solution() : queue(N) {}int countNodes(TreeNode* root) {if(root == nullptr){return 0;}int ans = 0;int l = 0, r = 0;queue[r++] = root;ans++;while(l < r){TreeNode* cur = queue[l++];if(cur->left){queue[r++] = cur->left;ans++;}if(cur->right){queue[r++] = cur->right;ans++;}}return ans;}
};

②通过高度实现优化：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private://计算树高int getHigh(TreeNode* root){if(root == nullptr){return 0;}int ans = 1;while(root->left){root = root->left;ans++;}return ans;}//由高度得到满二叉树的叶子结点个数int getNumsWithHigh(int h){if(h == 0){return 0;}return (1 << h) - 1;}public:int countNodes(TreeNode* root) {if(root == nullptr){return 0;}//左子树高int lh = getHigh(root->left);//右子树高int rh = getHigh(root->right);if(lh == rh){//如果左右子树高度相同，则左子树必定是满二叉树return getNumsWithHigh(lh) + countNodes(root->right) + 1;}else{//如果左右子树高度不同，则右子树必定是满二叉树return countNodes(root->left) + getNumsWithHigh(rh) + 1;}}
};

注：左老师的原代码，在此代码基础上优化了计算树高的过程，通过传递递归的树层减少while循环的次数。

最后，文章主要用于个人记录，如有错误还请指出和海涵，感谢阅读 ^_^