算法打卡16天
完全二叉树的节点个数
(力扣222题)
给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
完全二叉树 的定义如下:在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(从第 0 层开始),则该层包含 1~ 2h 个节点。
示例 1:
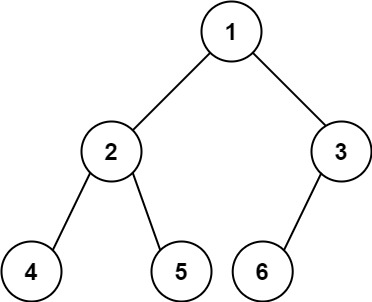
输入:root = [1,2,3,4,5,6]
输出:6
示例 2:
输入:root = []
输出:0
示例 3:
输入:root = [1]
输出:1
提示:
- 树中节点的数目范围是
[0, 5 * 104] 0 <= Node.val <= 5 * 104- 题目数据保证输入的树是 完全二叉树
**进阶:**遍历树来统计节点是一种时间复杂度为 O(n) 的简单解决方案。你可以设计一个更快的算法吗?
解题思路
题目要求计算完全二叉树的节点数。完全二叉树的性质是:如果左子树和右子树的深度相同,则该子树是满二叉树,其节点数可以通过公式 2深度−1 直接计算。算法通过递归计算左子树和右子树的深度:
- 如果左子树和右子树的深度相同,说明当前子树是满二叉树,直接返回节点数。
- 如果深度不同,则递归计算左子树和右子树的节点数,并加上当前节点(
+1)。 - 递归终止条件是当前节点为空,返回0。 这种方法利用了完全二叉树的性质,避免了逐个节点遍历,提高了效率。
代码
#include <iostream>
#include <stdlib.h>
struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution
{
public:int countNodes(TreeNode *root){if (root == NULL){return 0;}TreeNode *left = root->left;TreeNode *right = root->right;// 左右子树的深度int leftDepth = 0, rightDepth = 0;// 左子树的深度while (left){left = left->left;leftDepth++;}// 右子树的深度while (right){right = right->right;rightDepth++;}if(leftDepth == rightDepth ){// 注意(2<<1) 相当于2^2,返回满足满二叉树的子树节点数量return (2 << leftDepth) -1;}return countNodes( root->left) + countNodes( root->right) + 1;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(log n),算上了递归系统栈占用的空间
平衡二叉树
(力扣110题)
给定一个二叉树,判断它是否是 平衡二叉树
示例 1:
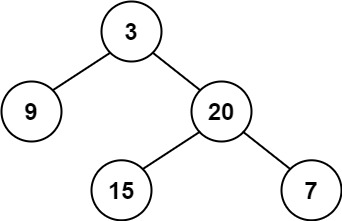
输入:root = [3,9,20,null,null,15,7]
输出:true
示例 2:
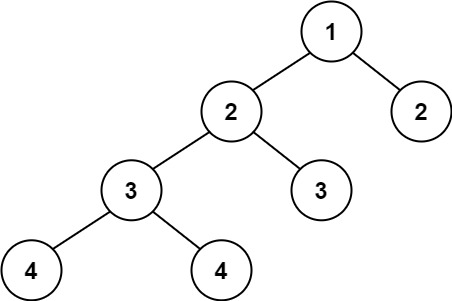
输入:root = [1,2,2,3,3,null,null,4,4]
输出:false
示例 3:
输入:root = []
输出:true
提示:
- 树中的节点数在范围
[0, 5000]内 -104 <= Node.val <= 104
解题思路
平衡二叉树的定义是:任意节点的左右子树高度差不超过1。为了判断一棵树是否是平衡二叉树,可以利用后序遍历(左右根)的思想,从底层叶子节点开始向上逐层计算高度,并判断是否满足平衡条件。
- 递归计算高度:通过递归函数
getHeight,计算每个节点的左右子树高度。 - 判断平衡条件:如果某个节点的左右子树高度差超过1,则返回特殊值
-1,表示该子树不平衡。 - 终止条件:如果当前节点为空,返回高度0。
- 返回结果:如果递归过程中返回了
-1,说明存在不平衡的子树,最终返回false;否则返回true。
这种方法通过后序遍历的方式,避免了重复计算子树高度,时间复杂度为O(n),空间复杂度为O(h)(h为树的高度)。
#include <iostream>
using namespace std;
#include <stdlib.h>
// 给定一个二叉树,判断它是否是 平衡二叉树
// 平衡二叉树就是任何一个左右子树高度都不大于1
// 使用后序遍历,因为求高度,高度是节点到叶子节点的距离,而后序是左右根,层层向上返回节点再加上直接的高度。
// 就是树的高度struct TreeNode
{int val;TreeNode *left;TreeNode *right;TreeNode() : val(0), left(nullptr), right(nullptr) {}TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};class Solution
{
public:int getHeight(TreeNode *root){// 终止条件if (root == nullptr){return 0;}// 左右子树高度int leftHeight = getHeight(root->left);if(leftHeight == -1){return -1;}int rightHeight = getHeight(root->right);if(rightHeight == -1){return -1;}return abs((leftHeight - rightHeight) > 1 ? -1 : max(leftHeight, rightHeight)+1) ;}boolisBalanced(TreeNode *root){return getHeight(root) == -1 ? false : true;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
二叉树的所有路径
(力扣257题)
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
示例 1:
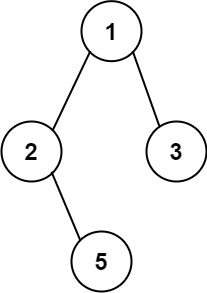
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
提示:
- 树中节点的数目在范围
[1, 100]内 -100 <= Node.val <= 100
解题思路
题目要求返回从根节点到所有叶子节点的路径。采用深度优先搜索(DFS)的方式,通过递归遍历二叉树,记录路径上的节点值。当到达叶子节点时,将路径转换为字符串格式并加入结果列表。
- 递归遍历:从根节点开始,逐层向下遍历,记录路径上的节点值。
- 叶子节点处理:到达叶子节点时,将路径转换为字符串(格式为“节点值->节点值…”),并存入结果列表。
- 回溯:在递归返回时,移除路径中最后一个节点值,以便继续探索其他路径。
- 终止条件:如果当前节点为空,直接返回。
通过这种方式,可以完整地记录所有从根节点到叶子节点的路径,时间复杂度为O(n),空间复杂度为O(h)(h为树的高度)。
代码
#include <iostream>
#include <vector>
using namespace std;
// 给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。// 叶子节点 是指没有子节点的节点。struct TreeNode
{int val;TreeNode *left;TreeNode *right;
};
class Solution
{
public:void traversal(TreeNode *cur, vector<int> &path, vector<string>& result){// 中,中为什么写在这里,因为最后一个节点也要加入到path中path.push_back(cur->val);// 叶子节点if(cur->left == NULL && cur->right == NULL){string PATH;for(int i = 0; i < path.size() - 1; i++){PATH += to_string(path[i]);PATH += "->";}PATH += to_string(path[path.size() - 1]);result.push_back(PATH);return ;}// 左if(cur->left){// 递归traversal(cur->left, path, result);//回溯path.pop_back();}// 右if(cur->right){// 递归traversal(cur->right, path, result);//回溯path.pop_back();}}vector<string> binaryTreePaths(TreeNode *root){// 结果vector<string> result;// 记录路径vector<int> path;if(root == NULL){return result;}traversal(root, path, result);return result;}
};
左叶子之和
(力扣404题)
给定二叉树的根节点 root ,返回所有左叶子之和。
示例 1:
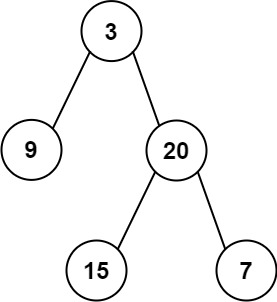
输入: root = [3,9,20,null,null,15,7]
输出: 24
解释: 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24
示例 2:
输入: root = [1]
输出: 0
提示:
- 节点数在
[1, 1000]范围内 -1000 <= Node.val <= 1000
解题思路
题目要求计算二叉树中所有左叶子节点的值之和。采用递归的后序遍历(左-右-中)方法来解决。
- 递归终止条件:
如果当前节点为空,直接返回0。如果当前节点是叶子节点(没有左右子节点),也返回0,因为叶子节点本身不是左叶子节点。 - 递归左子树:
递归计算左子树的左叶子节点之和。如果左子树是一个左叶子节点(即左子节点没有左右子节点),则将其值加入到leftValue中。 - 递归右子树:
递归计算右子树的左叶子节点之和。右子树中可能包含左叶子节点,因此需要继续递归。 - 计算总和:
将左子树和右子树的左叶子节点值相加,得到当前节点的左叶子节点之和。
通过这种方式,可以逐层递归遍历整棵树,确保所有左叶子节点的值都被正确计算。这种方法利用了后序遍历的思想,确保在处理当前节点时,左右子树的结果已经计算完成。
代码
#include <iostream>
#include <vector>
using namespace std;
// 左叶子之和
struct TreeNode
{int val;TreeNode *left;TreeNode *right;
};
// 后序遍历
class Solution
{public:int sumOfLeftLeaves(TreeNode *root){if (root == NULL){return 0;}// 如果是叶子节点if (root->left == NULL && root->right == NULL){return 0;}// 左int leftValue = sumOfLeftLeaves(root->left);// /遇到左叶子节点if (root->left && !root->left->left && !root->left->right){leftValue = root->left->val;}// 右int rightValue = sumOfLeftLeaves(root->right);// 中int sum = leftValue + rightValue;return sum;}
};
