随机响应噪声-极大似然估计

一、核心原因：噪声机制的数学可逆性

在随机响应机制（Randomized Response）中使用极大似然估计（Maximum Likelihood Estimation, MLE）是为了从扰动后的噪声数据中无偏地还原原始数据的统计特性。随机响应通过已知概率的扰动规则扭曲原始数据，其噪声过程满足：

1. 扰动概率是预先设定的（如 ​)；

2. 噪声分布是已知的（如实回答概率 p，随机回答概率 1−p）。

这使得我们可以建立观测数据（扰动后）与真实数据的概率映射关系，从而通过极大似然估计反推真实参数。

---

二、极大似然估计的推导过程

以二值数据（是/否）为例：

1. 真实数据分布：

   • 假设人群中回答“是”的真实比例为 θ（待估计）。

2. 扰动规则：

   • 以概率 p 如实回答；

   • 以概率 1−p随机回答（答“是”概率 0.5）。

3. 观测数据概率：

   • 观测到“是”的总概率：

     

4. 似然函数：

   • 对 n个用户，观测到 k个“是”，似然函数为：

     

5. 求解极大似然估计：

   • 最大化 ln⁡L(θ) 得到估计量：

     

---

三、为什么必须使用极大似然估计？

1. 无偏性保证

• 随机响应引入的噪声是系统性的（非随机噪声），传统均值计算会得到有偏结果。

• MLE 通过概率模型修正偏差，满足 （无偏估计）。

2. 信息充分利用

• MLE（极大似然估计） 基于所有观测数据的联合概率分布求解，比简单线性变换更高效利用信息。

3. 统计最优性

• 当样本量足够大时，MLE（极大似然估计） 是最小方差无偏估计（Cramér-Rao 下界）。

---

四、实例说明

场景：调查患病率（真实 θ=0.2)

• 参数设定：ϵ=ln⁡3 → p=0.75

• 100 个用户：

  • 真实患者 20 人：其中 20×0.75=15 人如实答“是”；

  • 健康者 80 人：其中 80×0.25×0.5=10 人随机答“是”。

• 总观测值：k=15+10=25（即 25% 答“是”）。

传统均值（错误估计）：

MLE 修正：

结果：（与真实值一致）。

五、数学本质：噪声的结构化概率模型

随机响应机制与拉普拉斯/高斯机制的核心差异在于噪声的生成逻辑与可逆性，这直接决定了为何需要极大似然估计（MLE）。

1. 随机响应：离散概率转移模型

随机响应的扰动过程是一个已知概率的离散信道，其本质是 条件概率的精确建模：

• 输入：真实数据 X∈{0,1}（例如 0=健康，1=患病）

• 输出：扰动数据 Y∈{0,1}

• 信道传输矩阵完全已知：

  

  关键特性：

  • 每个 P(Y∣X) 由预设规则显式定义（如)；

  • 模型满足 可逆性：可通过贝叶斯定理反推 P(X∣Y).

2. 拉普拉斯/高斯机制：不可逆的连续噪声

中心化差分隐私的噪声机制本质不同：

• 输入：标量或向量查询结果 

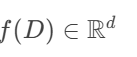
• 输出：

• 噪声完全随机化：

  • 从连续分布采样，丢失原始数据与噪声的对应关系；

  • 即使已知噪声分布，也无法唯一确定 f(D)（因方程 有无穷解）。

3. 为什么仅随机响应需要 MLE？

特性	随机响应机制	拉普拉斯/高斯机制
噪声类型	结构化概率转移	连续随机叠加
可逆性	✓ 通过概率模型精确还原	✗ 不可逆（信息有损）
参数估计目标	群体统计量 θ	单个查询结果 f(D)
估计方法	极大似然估计 (MLE)	直接发布扰动值

根本原因：

• 随机响应的目标是 从扰动数据反推群体参数（如患病率 θ），其噪声过程是 已知概率映射，因此可通过 MLE 构建似然函数求解 θ。

• 拉普拉斯/高斯机制的目标是 隐藏单个查询的真实值，添加的噪声本身即是保护手段，无需（也无法）从噪声中还原原始值。

总结

机制	噪声类型	估计方法	关键原因
随机响应	离散概率扰动	极大似然估计 (MLE)	噪声规则已知且可建模
拉普拉斯/高斯	连续随机噪声	直接发布扰动结果	噪声不可逆，仅能近似统计特性

核心结论：
随机响应机制中，只有通过极大似然估计才能从扰动数据中无偏还原真实参数，这是由其离散概率扰动特性决定的。随机响应机制的本质是一个人造的概率信道，其噪声规则是预先设计的结构化概率转移过程。这种结构保留了数据生成过程的完整数学描述，使得通过 MLE 无偏还原群体统计量成为可能。而连续噪声机制直接破坏原始数据的数值信息，其保护性依赖于噪声的不可逆性。