LCS 问题解释
最长公共子序列问题(Longest Common Subsequence),该问题可以表述为,在 A , B A,B A,B 中找出一段子序列 x x x,使得 x x x 既是 A A A 的子序列,又是 B B B 的子序列。

你可以理解为,在两个序列中分别删除一些元素(剩下的不一定连续),使得两个序列的剩余部分相同且长度最长。
暴力解法可以用 DFS,但是时间复杂度为 O ( ∣ A ∣ × 2 ∣ B ∣ ) O(|A|\times 2^{|B|}) O(∣A∣×2∣B∣),不能够满足我们的需求。
考虑动态规划。
定义:设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共子序列。
答案为 d p n , m dp_{n,m} dpn,m。
状态转移:
d p i , j = { d p i − 1 , j − 1 A i = B j max ( d p i − 1 , j , d p i , j − 1 ) otherwise dp_{i,j}=\begin{cases} dp_{i-1,j-1}& A_i=B_j\\ \max(dp_{i-1,j},dp_{i,j-1})&\text{otherwise} \end{cases} dpi,j={dpi−1,j−1max(dpi−1,j,dpi,j−1)Ai=Bjotherwise
但如果需要输出任意合法路径(题目:51Nod - 1006),怎么办?
递归倒推回去。
设 f ( x , y ) f(x,y) f(x,y) 表示 A A A 序列前 x x x 个和 B B B 序列前 y y y 个的匹配情况。
如果 A x = B y A_x=B_y Ax=By,那么说明选择了这个点,输出 A x A_x Ax(或 B y B_y By),同时调用 f ( x − 1 , y − 1 ) f(x-1,y-1) f(x−1,y−1)。
否则,如果 d p x − 1 , y > d p x , y − 1 dp_{x-1,y}>dp_{x,y-1} dpx−1,y>dpx,y−1,调用 f ( x − 1 , y ) f(x-1,y) f(x−1,y)。
否则调用 f ( x , y − 1 ) f(x,y-1) f(x,y−1)。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int dp[1005][1005];
string s,t;
void print(int x,int y){if(!x||!y){return;}if(s[x]==t[y]){print(x-1,y-1);cout<<s[x];}else{if(dp[x-1][y]>dp[x][y-1]){print(x-1,y);}else{print(x,y-1);}}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;s=' '+s,t=' '+t;for(int i=1;i<s.size();i++){for(int j=1;j<t.size();j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}print(s.size()-1,t.size()-1);return 0;
}
HDU-1159 Common Subsequence
最基础的那道题,本来应该放前面的。
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共子序列。
答案为 d p n , m dp_{n,m} dpn,m。
状态转移:
d p i , j = { d p i − 1 , j − 1 A i = B j max ( d p i − 1 , j , d p i , j − 1 ) otherwise dp_{i,j}=\begin{cases} dp_{i-1,j-1}& A_i=B_j\\ \max(dp_{i-1,j},dp_{i,j-1})&\text{otherwise} \end{cases} dpi,j={dpi−1,j−1max(dpi−1,j,dpi,j−1)Ai=Bjotherwise
注意:*.size() 类型为无符号整型,不管在哪个容器都一样。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int dp[1005][1005]; // 设 dp[i][j] 表示 A 串前 i 个字符和 B 串前 j 个字符的最长公共子序列
string s,t;
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);while(cin>>s>>t){s=' '+s,t=' '+t;for(int i=1;i<s.size();i++){for(int j=1;j<t.size();j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}cout<<dp[s.size()-1][t.size()-1]<<'\n';}return 0;
}
U118717 最长公共上升子序列
注意:该做法不太严谨,数据太水,本来应该会 TLE 的。
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列。
答案: max { d p i , j } \max\{dp_{i,j}\} max{dpi,j}。
计算前先进行 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j。
若 A i = B j A_i=B_j Ai=Bj,那么 d p i , j = max ( d p [ i ] [ j ] , 1 ) dp_{i,j}=\max(dp[i][j],1) dpi,j=max(dp[i][j],1)。
枚举 k ( k ∈ [ 1 , j − 1 ] ) k(k\in[1,j-1]) k(k∈[1,j−1]),若 b k < b j b_k<b_j bk<bj,则:
d p i , j = max ( d p i , j , d p i , k + 1 ) dp_{i,j}=\max(dp_{i,j},dp_{i,k}+1) dpi,j=max(dpi,j,dpi,k+1)
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,dp[3005][3005],a[3005],b[3005],ans;
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){cin>>b[i];}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j];if(a[i]==b[j]){dp[i][j]=max(dp[i-1][j],1ll);for(int k=1;k<j;k++){if(b[k]<b[j]){dp[i][j]=max(dp[i][j],dp[i][k]+1);}}}ans=max(ans,dp[i][j]);}}cout<<ans;return 0;
}
P2516 [HAOI2010] 最长公共子序列
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列, p a t h i , j path_{i,j} pathi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列的方案数。
先处理出 d p i , j dp_{i,j} dpi,j。然后考虑如何处理 p a t h i , j path_{i,j} pathi,j。
若 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j,说明是从 d p i − 1 , j dp_{i-1,j} dpi−1,j 转移过来的,那么:
p a t h i , j = ( p a t h i , j + p a t h i − 1 , j ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i-1,j})\bmod 10^8 pathi,j=(pathi,j+pathi−1,j)mod108
若 d p i , j = d p i , j − 1 dp_{i,j}=dp_{i,j-1} dpi,j=dpi,j−1,则:
p a t h i , j = ( p a t h i , j + p a t h i , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i,j-1})\bmod 10^8 pathi,j=(pathi,j+pathi,j−1)mod108
若 A i = B j A_i=B_j Ai=Bj 且 d p i , j = d p i − 1 , j − 1 + 1 dp_{i,j}=dp_{i-1,j-1}+1 dpi,j=dpi−1,j−1+1,则:
p a t h i , j = ( p a t h i , j + p a t h i − 1 , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i-1,j-1})\bmod 10^8 pathi,j=(pathi,j+pathi−1,j−1)mod108
若 d p i − 1 , j − 1 = d p i , j dp_{i-1,j-1}=dp_{i,j} dpi−1,j−1=dpi,j,那么说明 d p i − 1 , j − 1 dp_{i-1,j-1} dpi−1,j−1 会重复计算,则:
p a t h i , j = ( p a t h i , j − p a t h i − 1 , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}-path_{i-1,j-1})\bmod 10^8 pathi,j=(pathi,j−pathi−1,j−1)mod108
实现
#include<bits/stdc++.h>
using namespace std;
const int mod=1e8;
string s,t;
int dp[5005][5005],n,m,path[5005][5005];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;n=s.size(),m=t.size();s=' '+s,t=' '+t;n--,m--;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}for(int i=0;i<=m;i++){path[0][i]=1;}for(int i=0;i<=n;i++){path[i][0]=1;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(dp[i][j]==dp[i-1][j]){path[i][j]=(path[i][j]+path[i-1][j])%mod;}if(dp[i][j]==dp[i][j-1]){path[i][j]=(path[i][j]+path[i][j-1])%mod;}if(s[i]==t[j]&&dp[i][j]==dp[i-1][j-1]+1){path[i][j]=(path[i][j]+path[i-1][j-1])%mod;}if(dp[i-1][j-1]==dp[i][j]){path[i][j]=((path[i][j]-path[i-1][j-1])%mod+mod)%mod;}}}cout<<dp[n][m]<<'\n'<<path[n][m];return 0;
}
提交上去你就会发现是 70 70 70 分。
只有可怜的 125MB 空间显然过不了。
考虑滚动优化。
可以发现 p a t h path path 只涉及到 i − 1 i-1 i−1 和 i i i 层,可以开两个数字分别处理第 i i i 层和第 i − 1 i-1 i−1 层。
i − 1 i-1 i−1 层用 p r e pre pre,进行存储。
然后:
若 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j,说明是从 d p i − 1 , j dp_{i-1,j} dpi−1,j 转移过来的,那么:
p a t h j = ( p a t h j + p r e j ) m o d 10 8 path_j=(path_j+pre_j)\bmod 10^8 pathj=(pathj+prej)mod108
若 d p i , j = d p i , j − 1 dp_{i,j}=dp_{i,j-1} dpi,j=dpi,j−1,则:
p a t h j = ( p a t h j + p a t h j − 1 ) m o d 10 8 path_j=(path_j+path_{j-1})\bmod 10^8 pathj=(pathj+pathj−1)mod108
若 A i = B j A_i=B_j Ai=Bj 且 d p i , j = d p i − 1 , j − 1 + 1 dp_{i,j}=dp_{i-1,j-1}+1 dpi,j=dpi−1,j−1+1,则:
p a t h j = ( p a t h j + p r e j − 1 ) m o d 10 8 path_j=(path_j+pre_{j-1})\bmod 10^8 pathj=(pathj+prej−1)mod108
若 d p i − 1 , j − 1 = d p i , j dp_{i-1,j-1}=dp_{i,j} dpi−1,j−1=dpi,j,那么说明 d p i − 1 , j − 1 dp_{i-1,j-1} dpi−1,j−1 会重复计算,则:
p a t h i , j = ( p a t h i , j − p r e j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}-pre_{j-1})\bmod 10^8 pathi,j=(pathi,j−prej−1)mod108
初始化:
i ∈ [ 0 , m ] , p r e i = 1 i ∈ [ 0 , n ] , p a t h i = 1 i\in[0,m],pre_i=1\\ i\in[0,n],path_i=1 i∈[0,m],prei=1i∈[0,n],pathi=1
注意: p a t h path path 数组每一层都需要清空。
实现
#include<bits/stdc++.h>
using namespace std;
const int mod=1e8;
string s,t;
int dp[5005][5005],n,m,path[5005],pre[5005];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;n=s.size(),m=t.size();s=' '+s,t=' '+t;n--,m--;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}for(int i=0;i<=m;i++){pre[i]=1;}for(int i=0;i<=n;i++){path[i]=1;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){path[j]=0;if(dp[i][j]==dp[i-1][j]){path[j]=(path[j]+pre[j])%mod;}if(dp[i][j]==dp[i][j-1]){path[j]=(path[j]+path[j-1])%mod;}if(s[i]==t[j]&&dp[i][j]==dp[i-1][j-1]+1){path[j]=(path[j]+pre[j-1])%mod;}if(dp[i-1][j-1]==dp[i][j]){path[j]=((path[j]-pre[j-1])%mod+mod)%mod;}}for(int j=1;j<=m;j++){pre[j]=path[j];}}cout<<dp[n][m]<<'\n'<<path[m];return 0;
}
```最长公共子序列问题(Longest Common Subsequence),该问题可以表述为,在 $A,B$ 中找出一段子序列 $x$,使得 $x$ 既是 $A$ 的子序列,又是 $B$ 的子序列。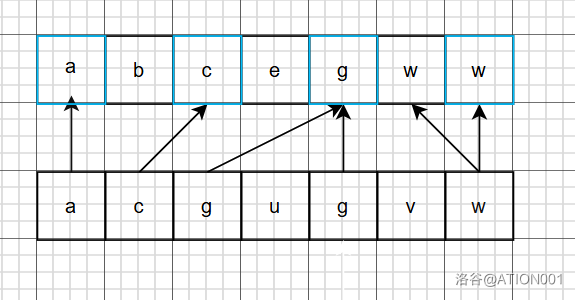你可以理解为,在两个序列中分别删除一些元素(剩下的不一定连续),使得两个序列的剩余部分相同且长度最长。暴力解法可以用 DFS,但是时间复杂度为 $O(|A|\times 2^{|B|})$,不能够满足我们的需求。考虑动态规划。定义:设 $dp_{i,j}$ 表示 $A$ 序列前 $i$ 个与 $B$ 序列的前 $j$ 个的最长公共子序列。答案为 $dp_{n,m}$。状态转移:$$
dp_{i,j}=\begin{cases}
dp_{i-1,j-1}& A_i=B_j\\
\max(dp_{i-1,j},dp_{i,j-1})&\text{otherwise}
\end{cases}
$$但如果需要输出任意合法路径(题目:[51Nod - 1006](https://vjudge.net/problem/51Nod-1006)),怎么办?递归倒推回去。设 $f(x,y)$ 表示 $A$ 序列前 $x$ 个和 $B$ 序列前 $y$ 个的匹配情况。如果 $A_x=B_y$,那么说明选择了这个点,输出 $A_x$(或 $B_y$),同时调用 $f(x-1,y-1)$。否则,如果 $dp_{x-1,y}>dp_{x,y-1}$,调用 $f(x-1,y)$。否则调用 $f(x,y-1)$。
### 实现
```cpp
#include<bits/stdc++.h>
using namespace std;
#define int long long
int dp[1005][1005];
string s,t;
void print(int x,int y){if(!x||!y){return;}if(s[x]==t[y]){print(x-1,y-1);cout<<s[x];}else{if(dp[x-1][y]>dp[x][y-1]){print(x-1,y);}else{print(x,y-1);}}
}
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;s=' '+s,t=' '+t;for(int i=1;i<s.size();i++){for(int j=1;j<t.size();j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}print(s.size()-1,t.size()-1);return 0;
}
HDU-1159 Common Subsequence
最基础的那道题,本来应该放前面的。
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共子序列。
答案为 d p n , m dp_{n,m} dpn,m。
状态转移:
d p i , j = { d p i − 1 , j − 1 A i = B j max ( d p i − 1 , j , d p i , j − 1 ) otherwise dp_{i,j}=\begin{cases} dp_{i-1,j-1}& A_i=B_j\\ \max(dp_{i-1,j},dp_{i,j-1})&\text{otherwise} \end{cases} dpi,j={dpi−1,j−1max(dpi−1,j,dpi,j−1)Ai=Bjotherwise
注意:*.size() 类型为无符号整型,不管在哪个容器都一样。
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int dp[1005][1005]; // 设 dp[i][j] 表示 A 串前 i 个字符和 B 串前 j 个字符的最长公共子序列
string s,t;
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);while(cin>>s>>t){s=' '+s,t=' '+t;for(int i=1;i<s.size();i++){for(int j=1;j<t.size();j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}cout<<dp[s.size()-1][t.size()-1]<<'\n';}return 0;
}
U118717 最长公共上升子序列
注意:该做法不太严谨,数据太水,本来应该会 TLE 的。
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列。
答案: max { d p i , j } \max\{dp_{i,j}\} max{dpi,j}。
计算前先进行 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j。
若 A i = B j A_i=B_j Ai=Bj,那么 d p i , j = max ( d p [ i ] [ j ] , 1 ) dp_{i,j}=\max(dp[i][j],1) dpi,j=max(dp[i][j],1)。
枚举 k ( k ∈ [ 1 , j − 1 ] ) k(k\in[1,j-1]) k(k∈[1,j−1]),若 b k < b j b_k<b_j bk<bj,则:
d p i , j = max ( d p i , j , d p i , k + 1 ) dp_{i,j}=\max(dp_{i,j},dp_{i,k}+1) dpi,j=max(dpi,j,dpi,k+1)
实现
#include<bits/stdc++.h>
using namespace std;
#define int long long
int n,dp[3005][3005],a[3005],b[3005],ans;
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>n;for(int i=1;i<=n;i++){cin>>a[i];}for(int i=1;i<=n;i++){cin>>b[i];}for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){dp[i][j]=dp[i-1][j];if(a[i]==b[j]){dp[i][j]=max(dp[i-1][j],1ll);for(int k=1;k<j;k++){if(b[k]<b[j]){dp[i][j]=max(dp[i][j],dp[i][k]+1);}}}ans=max(ans,dp[i][j]);}}cout<<ans;return 0;
}
P2516 [HAOI2010] 最长公共子序列
设 d p i , j dp_{i,j} dpi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列, p a t h i , j path_{i,j} pathi,j 表示 A A A 序列前 i i i 个与 B B B 序列的前 j j j 个的最长公共上升子序列的方案数。
先处理出 d p i , j dp_{i,j} dpi,j。然后考虑如何处理 p a t h i , j path_{i,j} pathi,j。
若 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j,说明是从 d p i − 1 , j dp_{i-1,j} dpi−1,j 转移过来的,那么:
p a t h i , j = ( p a t h i , j + p a t h i − 1 , j ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i-1,j})\bmod 10^8 pathi,j=(pathi,j+pathi−1,j)mod108
若 d p i , j = d p i , j − 1 dp_{i,j}=dp_{i,j-1} dpi,j=dpi,j−1,则:
p a t h i , j = ( p a t h i , j + p a t h i , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i,j-1})\bmod 10^8 pathi,j=(pathi,j+pathi,j−1)mod108
若 A i = B j A_i=B_j Ai=Bj 且 d p i , j = d p i − 1 , j − 1 + 1 dp_{i,j}=dp_{i-1,j-1}+1 dpi,j=dpi−1,j−1+1,则:
p a t h i , j = ( p a t h i , j + p a t h i − 1 , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}+path_{i-1,j-1})\bmod 10^8 pathi,j=(pathi,j+pathi−1,j−1)mod108
若 d p i − 1 , j − 1 = d p i , j dp_{i-1,j-1}=dp_{i,j} dpi−1,j−1=dpi,j,那么说明 d p i − 1 , j − 1 dp_{i-1,j-1} dpi−1,j−1 会重复计算,则:
p a t h i , j = ( p a t h i , j − p a t h i − 1 , j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}-path_{i-1,j-1})\bmod 10^8 pathi,j=(pathi,j−pathi−1,j−1)mod108
实现
#include<bits/stdc++.h>
using namespace std;
const int mod=1e8;
string s,t;
int dp[5005][5005],n,m,path[5005][5005];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;n=s.size(),m=t.size();s=' '+s,t=' '+t;n--,m--;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}for(int i=0;i<=m;i++){path[0][i]=1;}for(int i=0;i<=n;i++){path[i][0]=1;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(dp[i][j]==dp[i-1][j]){path[i][j]=(path[i][j]+path[i-1][j])%mod;}if(dp[i][j]==dp[i][j-1]){path[i][j]=(path[i][j]+path[i][j-1])%mod;}if(s[i]==t[j]&&dp[i][j]==dp[i-1][j-1]+1){path[i][j]=(path[i][j]+path[i-1][j-1])%mod;}if(dp[i-1][j-1]==dp[i][j]){path[i][j]=((path[i][j]-path[i-1][j-1])%mod+mod)%mod;}}}cout<<dp[n][m]<<'\n'<<path[n][m];return 0;
}
提交上去你就会发现是 70 70 70 分。
只有可怜的 125MB 空间显然过不了。
考虑滚动优化。
可以发现 p a t h path path 只涉及到 i − 1 i-1 i−1 和 i i i 层,可以开两个数字分别处理第 i i i 层和第 i − 1 i-1 i−1 层。
i − 1 i-1 i−1 层用 p r e pre pre,进行存储。
然后:
若 d p i , j = d p i − 1 , j dp_{i,j}=dp_{i-1,j} dpi,j=dpi−1,j,说明是从 d p i − 1 , j dp_{i-1,j} dpi−1,j 转移过来的,那么:
p a t h j = ( p a t h j + p r e j ) m o d 10 8 path_j=(path_j+pre_j)\bmod 10^8 pathj=(pathj+prej)mod108
若 d p i , j = d p i , j − 1 dp_{i,j}=dp_{i,j-1} dpi,j=dpi,j−1,则:
p a t h j = ( p a t h j + p a t h j − 1 ) m o d 10 8 path_j=(path_j+path_{j-1})\bmod 10^8 pathj=(pathj+pathj−1)mod108
若 A i = B j A_i=B_j Ai=Bj 且 d p i , j = d p i − 1 , j − 1 + 1 dp_{i,j}=dp_{i-1,j-1}+1 dpi,j=dpi−1,j−1+1,则:
p a t h j = ( p a t h j + p r e j − 1 ) m o d 10 8 path_j=(path_j+pre_{j-1})\bmod 10^8 pathj=(pathj+prej−1)mod108
若 d p i − 1 , j − 1 = d p i , j dp_{i-1,j-1}=dp_{i,j} dpi−1,j−1=dpi,j,那么说明 d p i − 1 , j − 1 dp_{i-1,j-1} dpi−1,j−1 会重复计算,则:
p a t h i , j = ( p a t h i , j − p r e j − 1 ) m o d 10 8 path_{i,j}=(path_{i,j}-pre_{j-1})\bmod 10^8 pathi,j=(pathi,j−prej−1)mod108
初始化:
i ∈ [ 0 , m ] , p r e i = 1 i ∈ [ 0 , n ] , p a t h i = 1 i\in[0,m],pre_i=1\\ i\in[0,n],path_i=1 i∈[0,m],prei=1i∈[0,n],pathi=1
注意: p a t h path path 数组每一层都需要清空。
实现
#include<bits/stdc++.h>
using namespace std;
const int mod=1e8;
string s,t;
int dp[5005][5005],n,m,path[5005],pre[5005];
signed main(){ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);cin>>s>>t;n=s.size(),m=t.size();s=' '+s,t=' '+t;n--,m--;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(s[i]==t[j]){dp[i][j]=dp[i-1][j-1]+1;}else{dp[i][j]=max(dp[i-1][j],dp[i][j-1]);}}}for(int i=0;i<=m;i++){pre[i]=1;}for(int i=0;i<=n;i++){path[i]=1;}for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){path[j]=0;if(dp[i][j]==dp[i-1][j]){path[j]=(path[j]+pre[j])%mod;}if(dp[i][j]==dp[i][j-1]){path[j]=(path[j]+path[j-1])%mod;}if(s[i]==t[j]&&dp[i][j]==dp[i-1][j-1]+1){path[j]=(path[j]+pre[j-1])%mod;}if(dp[i-1][j-1]==dp[i][j]){path[j]=((path[j]-pre[j-1])%mod+mod)%mod;}}for(int j=1;j<=m;j++){pre[j]=path[j];}}cout<<dp[n][m]<<'\n'<<path[m];return 0;
}
