当前位置：首页 > news >正文

【编译原理】语法分析方法总结

news 来源：原创 2025/6/10 5:05:49

一、预测分析法

整体结构

1. 核心条件：LL(1)文法

2. 预测分析表的构造

3. 分析过程

二、算符优先分析法

整体结构

优先函数

1. 核心条件：算符文法（OG）与算符优先文法（OPG）

2. 关键集合：FIRSTVT 与 LASTVT

3. 优先关系定义

4. 优先关系矩阵与优先函数

5. 分析过程

三、LR分析法

整体结构

1. LR分析法概述

2. LR(0) 分析法

3. SLR(1) 分析法

4. LR(1) 分析法

一、预测分析法

确定的自上而下语法分析方法，适用于LL(1)文法

其核心是通过预测分析表（LL(1)分析表）和栈结构，唯一确定每一步推导（最左推导）使用的产生式，避免回溯

整体结构

1. 核心条件：LL(1)文法

预测分析法要求文法满足以下条件：

无左递归（直接或间接）。
候选式的FIRST集互不相交：对同一非终结符的不同候选式，其首符号集无交集。
ε候选式的处理：若某候选式可推出ε，则该非终结符的FOLLOW集与其他候选式的FIRST集无交集。

2. 预测分析表的构造

步骤：

计算FIRST集：
- 终结符的FIRST集为自身。
- 非终结符的FIRST集由其产生式右部的首符号决定，递归推导直至遇到终结符或ε。
计算FOLLOW集：
- 开始符号的FOLLOW集包含#。
- 若存在产生式A→αBβ，则FIRST(β)-{ε}加入FOLLOW(B)。
- 若β可推导出ε，则将FOLLOW(A)加入FOLLOW(B)。
填充分析表：
- 对每个产生式A→α：
  - 若a ∈ FIRST(α)，则M[A, a] = A→α。
  - 若α可推导出ε，则对b ∈ FOLLOW(A)，M[A, b] = A→α。

3. 分析过程

数据结构：

分析栈：初始为#和文法的开始符号（如E）。
输入串：末尾添加#作为结束符。

步骤：

栈顶为终结符：
- 若与当前输入符号匹配，弹出栈顶，输入指针后移。
- 若不匹配，报错。
栈顶为非终结符：
- 查预测分析表M[X, a]，找到产生式X→α。
- 弹出X，将α逆序压入栈（如α=XYZ，则压入Z Y X）。
成功条件：
- 栈顶和输入符号均为#，分析成功。
失败条件：
- 查表无对应产生式，报错。

自下而上分析方法是从输入符号串开始，查找当前句柄，并用产生式将它归约成相应的非终结符号，最后归约为开始符号的一种分析方法

(1)对输入符号串的扫描，采用自左向右的顺序；

(2)分析过程是自下而上进行的(对语法树来说从末端结点开始，最后归约到根结点)；

(3)每次归约是对最左简单短语(句柄)进行的；

(4)算法的关键是确定最左简单短语。

二、算符优先分析法

算符优先分析法是一种自下而上的语法分析方法，特别适合处理表达式

其核心是通过终结符之间的优先关系确定归约顺序，而非严格遵循规范归约

整体结构

优先函数

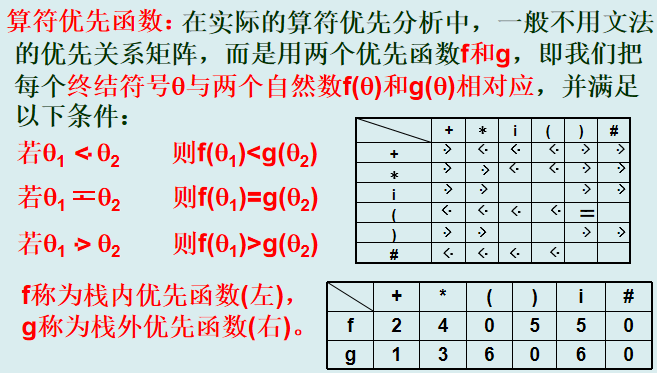
优点：

编程时便于比较运算，即用一般的关系运算即可;

比用文法的优先关系矩阵节省内存，若有n个终结符号，优先关系矩阵占内存为(n+1)2，优先函数为2(n+1);

缺点：

本来不存在优先关系的两个终结符号，变成可比较了，不易发现语法错误。

注意：

应区别对待一目运算“减”和二目运算“减”，它们虽然使用相同的符号‘-’，但优先级不同，可使用不同的符号代替一目运算“减”，即看成两种运算。

1. 核心条件：算符文法（OG）与算符优先文法（OPG）

算符文法（OG）：文法中任意产生式的右部不含连续的非终结符。

算符优先文法（OPG）：OG基础上，任意两终结符之间至多一种优先关系（<, =, >）。

2. 关键集合：FIRSTVT 与 LASTVT

FIRSTVT(U)：非终结符U能推导出的所有符号串的第一个终结符。
LASTVT(U)：非终结符U能推导出的所有符号串的最后一个终结符。
计算方法：
- FIRSTVT：若产生式形如 U→b... 或 U→Vb...，则 b ∈ FIRSTVT(U)。
- LASTVT：若产生式形如 U→...a 或 U→...aV，则 a ∈ LASTVT(U)。

3. 优先关系定义

a < b：若存在产生式 U→...aV...，且 b ∈ FIRSTVT(V)。
a = b：若存在产生式 U→...ab... 或 U→...aVb...。
a > b：若存在产生式 U→...Vb...，且 a ∈ LASTVT(V)。

4. 优先关系矩阵与优先函数

优先关系矩阵：矩阵的行和列为终结符，元素为 <, =, >。
优先函数（f和g）：将终结符映射为整数，满足：
- 若 a < b，则 f(a) < g(b)；
- 若 a = b，则 f(a) = g(b)；
- 若 a > b，则 f(a) > g(b)。

5. 分析过程

数据结构：

符号栈：存放已分析的符号。
输入串：末尾添加结束符 #。

步骤：

初始化：将 # 压入符号栈，输入指针指向第一个符号。
比较优先级：
- 栈顶终结符为 a，输入符号为 b。
- 若 a < b 或 a = b，移进 b。
- 若 a > b，归约最左素短语。
归约规则：
- 找到栈顶最左素短语（至少含一个终结符，且无更小素短语）。
- 用对应的非终结符替换素短语。
结束条件：
- 栈中只剩 #S（S为开始符号），输入为 #，分析成功。
- 若无法匹配优先级，报错。

三、LR分析法

整体结构

1. LR分析法概述

LR分析法是一种有效的自底向上的语法分析技术，它能适用于大部分上下文无关文法的分析，一般叫 LR(k)分析方法，其中L是指自左(Left)向右扫描输入单词串，R是指分析过程都是构造最右(Right)推导的逆过程(规范归约)，括号中的k是指在决定当前分析动作时向前看的符号个数

核心思想：自下而上语法分析，通过构造分析表（动作表 Action 和状态转换表 Goto）驱动分析过程。
特点：

L：从左向右扫描输入串
R：构造最右推导的逆过程（规范归约）
k：向前看 k 个符号（通常 k=1）

分析过程：

初始化：栈中压入初始状态 S0 和 #（输入串边界符）。
查表决策：
- 移进（Shift）：将输入符号和对应新状态压栈。
- 归约（Reduce）：按产生式替换栈顶符号，查 Goto 表更新状态。
- 接受（Accept）：栈顶为开始符号，输入为 #。
- 报错：无合法动作。

2. LR(0) 分析法

核心：基于 LR(0) 项目集规范族，每个状态不含冲突（移进-归约或归约-归约）。
步骤：

拓广文法：添加 S'→S，确保唯一接受状态。
构造项目集：
- LR(0) 项目：形如 A→α·β，圆点表示分析进度。
- 闭包（Closure）：若 A→α·Bβ，则加入 B→·γ 的所有产生式。
- 转换函数（Goto）：根据符号 X 转移到新状态。
构造分析表：
- 移进：Action[S_i, a] = S_j（a 是终结符）。
- 归约：若 A→α·，则 Action[S_i, *] = r_k（k 为产生式编号）。
- 接受：S'→S· 时 Action[S_i, #] = acc。

缺点：无法处理冲突（需文法为 LR(0) 文法）。

3. SLR(1) 分析法

改进：在 LR(0) 基础上，利用 Follow 集 解决冲突。
冲突解决规则：

若状态中存在 A→α· 和 B→β·aγ，且 a ∈ Follow(A)，则对 a 选择移进，其他符号归约。

步骤：

构造 LR(0) 项目集。
填充分析表：
- 归约动作仅对 a ∈ Follow(A) 生效（Action[S_i, a] = r_k）。

优点：比 LR(0) 更灵活，适用于更多文法。
缺点：若 Follow(A) 与移进符号有交集，仍无法解决冲突。

4. LR(1) 分析法

核心：引入 向前搜索符（Lookahead），每个项目形式为 [A→α·β, a]，表示归约时需匹配 a。
步骤：

构造 LR(1) 项目集：
- 闭包：若 [A→α·Bβ, a]，则加入 [B→·γ, b]，其中 b ∈ First(βa)。
- 转换函数：类似 LR(0)，但携带向前搜索符。
构造分析表：
- 归约动作仅在输入符与向前搜索符匹配时触发（Action[S_i, a] = r_k）。

优点：解决 SLR(1) 无法处理的冲突（如 Follow 集与移进符号重叠）。
缺点：项目集数量庞大，构造复杂度高。

方法	核心机制	冲突解决	复杂度	适用性
LR(0)	无冲突项目集	无法处理冲突	低	严格无冲突文法
SLR(1)	利用 `Follow` 集	解决部分移进-归约冲突	中	多数程序设计语言
LR(1)	向前搜索符（精确匹配）	解决所有 LR 冲突	高	复杂或二义性文法