python打卡训练营打卡记录day34
- CPU性能的查看:看架构代际、核心数、线程数
- GPU性能的查看:看显存、看级别、看架构代际
- GPU训练的方法:数据和模型移动到GPU device上
- 类的call方法:为什么定义前向传播时可以直接写作self.fc1(x)
作业:
复习今天的内容,在巩固下代码。思考下为什么会出现这个问题。
检查CUDA是否可用
import torch# 检查CUDA是否可用
if torch.cuda.is_available():print("CUDA可用!")# 获取可用的CUDA设备数量device_count = torch.cuda.device_count()print(f"可用的CUDA设备数量: {device_count}")# 获取当前使用的CUDA设备索引current_device = torch.cuda.current_device()print(f"当前使用的CUDA设备索引: {current_device}")# 获取当前CUDA设备的名称device_name = torch.cuda.get_device_name(current_device)print(f"当前CUDA设备的名称: {device_name}")# 获取CUDA版本cuda_version = torch.version.cudaprint(f"CUDA版本: {cuda_version}")# 查看cuDNN版本(如果可用)print("cuDNN版本:", torch.backends.cudnn.version())else:print("CUDA不可用。")CUDA可用!
可用的CUDA设备数量: 1
当前使用的CUDA设备索引: 0
当前CUDA设备的名称: NVIDIA GeForce RTX 3060 Laptop GPU
CUDA版本: 12.1
cuDNN版本: 90100设置GPU设备
# 设置GPU设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")使用设备: cuda:0GPU训练
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征数据
y = iris.target # 标签数据# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 归一化数据
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 将数据转换为PyTorch张量并移至GPU
# 分类问题交叉熵损失要求标签为long类型
# 张量具有to(device)方法,可以将张量移动到指定的设备上
X_train = torch.FloatTensor(X_train).to(device)
y_train = torch.LongTensor(y_train).to(device)
X_test = torch.FloatTensor(X_test).to(device)
y_test = torch.LongTensor(y_test).to(device)
class MLP(nn.Module):def __init__(self):super(MLP, self).__init__()self.fc1 = nn.Linear(4, 10)self.relu = nn.ReLU()self.fc2 = nn.Linear(10, 3)def forward(self, x):out = self.fc1(x)out = self.relu(out)out = self.fc2(out)return out# 实例化模型并移至GPU
# MLP继承nn.Module类,所以也具有to(device)方法
model = MLP().to(device)
# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 20000
losses = []import time
start_time = time.time() # 记录开始时间for epoch in range(num_epochs):# 前向传播outputs = model(X_train)loss = criterion(outputs, y_train)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()# 记录损失值losses.append(loss.item())# 打印训练信息if (epoch + 1) % 100 == 0:print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')time_all = time.time() - start_time
print(f'Training time: {time_all:.2f} seconds')# 可视化损失曲线
plt.plot(range(num_epochs), losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.show()Epoch [100/20000], Loss: 1.0852
Epoch [200/20000], Loss: 1.0721
Epoch [300/20000], Loss: 1.0540
Epoch [400/20000], Loss: 1.0292
Epoch [500/20000], Loss: 0.9956
Epoch [600/20000], Loss: 0.9511
Epoch [700/20000], Loss: 0.8956
Epoch [800/20000], Loss: 0.8317
Epoch [900/20000], Loss: 0.7652
Epoch [1000/20000], Loss: 0.7023
Epoch [1100/20000], Loss: 0.6474
Epoch [1200/20000], Loss: 0.6010
Epoch [1300/20000], Loss: 0.5624
Epoch [1400/20000], Loss: 0.5304
Epoch [1500/20000], Loss: 0.5035
Epoch [1600/20000], Loss: 0.4804
Epoch [1700/20000], Loss: 0.4601
Epoch [1800/20000], Loss: 0.4420
Epoch [1900/20000], Loss: 0.4255
Epoch [2000/20000], Loss: 0.4103
Epoch [2100/20000], Loss: 0.3960
Epoch [2200/20000], Loss: 0.3827
Epoch [2300/20000], Loss: 0.3699
Epoch [2400/20000], Loss: 0.3578
Epoch [2500/20000], Loss: 0.3462
...
Epoch [19800/20000], Loss: 0.0617
Epoch [19900/20000], Loss: 0.0616
Epoch [20000/20000], Loss: 0.0615
Training time: 11.99 seconds
你这时可能会好奇,不是说gpu比cpu快很多吗?怎么cpu跑了3s,gpu跑了11s。
你问AI,他会告诉你,对于非常小的数据集和简单的模型,CPU 通常会比 GPU 更快。实际上,这并非本质的原因。
这需要你进一步理解二者的区别,深度学习项目的运行时长往往很长,如果只停留在跑通的层面,那是不够的。
本质是因为GPU在计算的时候,相较于cpu多了3个时间上的开销
1. 数据传输开销 (CPU 内存 <-> GPU 显存)
2. 核心启动开销 (GPU 核心启动时间)
3. 性能浪费:计算量和数据批次
下面详细介绍下
数据传输开销 (CPU 内存 <-> GPU 显存)
在 GPU 进行任何计算之前,数据(输入张量 X_train、y_train,模型参数)需要从计算机的主内存 (RAM) 复制到 GPU 专用的显存 (VRAM) 中。
当结果传回 CPU 时(例如,使用 loss.item() 获取损失值用于打印或记录,或者获取最终预测结果),数据也需要从 GPU 显存复制回 CPU 内存。
对于少量数据和非常快速的计算任务,这个传输时间可能比 GPU 通过并行计算节省下来的时间还要长。
在上述代码中,循环里的 loss.item() 操作会在每个 epoch 都进行一次从 GPU 到 CPU 的数据同步和传输,以便获取标量损失值。对于20000个epoch来说,这会累积不少的传输开销。
核心启动开销 (GPU 核心启动时间)
GPU 执行的每个操作(例如,一个线性层的前向传播、一个激活函数)都涉及到在 GPU 上启动一个“核心”(kernel)——一个在 GPU 众多计算单元上运行的小程序。
启动每个核心都有一个小的、固定的开销。
如果核心内的实际计算量非常小(本项目的小型网络和鸢尾花数据),这个启动开销在总时间中的占比就会比较大。相比之下,CPU 执行这些小操作的“调度”开销通常更低。
性能浪费:计算量和数据批次
这个数据量太少,gpu的很多计算单元都没有被用到,即使用了全批次也没有用到的全部计算单元。
综上,数据传输和各种固定开销的总和,超过了 GPU 在这点计算量上通过并行处理所能节省的时间,导致了 GPU 比 CPU 慢的现象。
1.CPU (12th Gen Intel Core i9-12900KF): 对于这种小任务,CPU 的单核性能强劲,且没有显著的数据传输到“另一块芯片”的开销。它可以非常迅速地完成计算。
2.GPU (NVIDIA GeForce RTX 3080 Ti):需要花费时间将数据和模型从 CPU 内存移动到 GPU 显存。
3.每次在 GPU 上执行运算(如 model(X_train)、loss.backward()) 都有核心启动的固定开销。
4.oss.item() 在每个 epoch 都需要将结果从 GPU 传回 CPU,这在总共 20000 个 epoch 中会累积。
5.GPU 强大的并行计算能力在这种小任务上完全没有用武之地。
这些特性导致GPU在处理鸢尾花分类这种“玩具级别”的问题时,它的优势无法体现,反而会因为上述开销显得“笨重”。
那么什么时候 GPU 会发挥巨大优势?
1.大型数据集: 例如,图像数据集成千上万张图片,每张图片维度很高。
2.大型模型: 例如,深度卷积网络 (CNNs like ResNet, VGG) 或 Transformer 模型,它们有数百万甚至数十亿的参数,计算量巨大。
3.合适的批处理大小: 能够充分利用 GPU 并行性的 batch size,不至于还有剩余的计算量没有被 GPU 处理。
4.复杂的、可并行的运算: 大量的矩阵乘法、卷积等。
针对上面反应的3个问题,能够优化的只有数据传输时间,针对性解决即可,很容易想到2个思路:
1. 直接不打印训练过程的loss了,但是这样会没办法记录最后的可视化图片,只能肉眼观察loss数值变化。
2. 每隔200个epoch保存一下loss,不需要20000个epoch每次都打印,
下面先尝试第一个思路:
# 知道了哪里耗时,针对性优化一下
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import numpy as np# 仍然用4特征,3分类的鸢尾花数据集作为我们今天的数据集
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征数据
y = iris.target # 标签数据
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# # 打印下尺寸
# print(X_train.shape)
# print(y_train.shape)
# print(X_test.shape)
# print(y_test.shape)# 归一化数据,神经网络对于输入数据的尺寸敏感,归一化是最常见的处理方式
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test) #确保训练集和测试集是相同的缩放# 将数据转换为 PyTorch 张量,因为 PyTorch 使用张量进行训练
# y_train和y_test是整数,所以需要转化为long类型,如果是float32,会输出1.0 0.0
X_train = torch.FloatTensor(X_train)
y_train = torch.LongTensor(y_train)
X_test = torch.FloatTensor(X_test)
y_test = torch.LongTensor(y_test)class MLP(nn.Module): # 定义一个多层感知机(MLP)模型,继承父类nn.Moduledef __init__(self): # 初始化函数super(MLP, self).__init__() # 调用父类的初始化函数# 前三行是八股文,后面的是自定义的self.fc1 = nn.Linear(4, 10) # 输入层到隐藏层self.relu = nn.ReLU()self.fc2 = nn.Linear(10, 3) # 隐藏层到输出层
# 输出层不需要激活函数,因为后面会用到交叉熵函数cross_entropy,交叉熵函数内部有softmax函数,会把输出转化为概率def forward(self, x):out = self.fc1(x)out = self.relu(out)out = self.fc2(out)return out# 实例化模型
model = MLP()# 分类问题使用交叉熵损失函数
criterion = nn.CrossEntropyLoss()# 使用随机梯度下降优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)# # 使用自适应学习率的化器
# optimizer = optim.Adam(model.parameters(), lr=0.001)# 训练模型
num_epochs = 20000 # 训练的轮数# 用于存储每个 epoch 的损失值
losses = []import time
start_time = time.time() # 记录开始时间for epoch in range(num_epochs): # range是从0开始,所以epoch是从0开始# 前向传播outputs = model.forward(X_train) # 显式调用forward函数# outputs = model(X_train) # 常见写法隐式调用forward函数,其实是用了model类的__call__方法loss = criterion(outputs, y_train) # output是模型预测值,y_train是真实标签# 反向传播和优化optimizer.zero_grad() #梯度清零,因为PyTorch会累积梯度,所以每次迭代需要清零,梯度累计是那种小的bitchsize模拟大的bitchsizeloss.backward() # 反向传播计算梯度optimizer.step() # 更新参数# 记录损失值# losses.append(loss.item())# 打印训练信息if (epoch + 1) % 100 == 0: # range是从0开始,所以epoch+1是从当前epoch开始,每100个epoch打印一次print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')time_all = time.time() - start_time # 计算训练时间
print(f'Training time: {time_all:.2f} seconds')Epoch [100/20000], Loss: 1.0540
Epoch [200/20000], Loss: 1.0179
Epoch [300/20000], Loss: 0.9744
Epoch [400/20000], Loss: 0.9236
Epoch [500/20000], Loss: 0.8691
Epoch [600/20000], Loss: 0.8127
Epoch [700/20000], Loss: 0.7568
Epoch [800/20000], Loss: 0.7040
Epoch [900/20000], Loss: 0.6560
Epoch [1000/20000], Loss: 0.6138
Epoch [1100/20000], Loss: 0.5773
Epoch [1200/20000], Loss: 0.5456
Epoch [1300/20000], Loss: 0.5180
Epoch [1400/20000], Loss: 0.4938
Epoch [1500/20000], Loss: 0.4726
Epoch [1600/20000], Loss: 0.4536
Epoch [1700/20000], Loss: 0.4366
Epoch [1800/20000], Loss: 0.4211
Epoch [1900/20000], Loss: 0.4068
Epoch [2000/20000], Loss: 0.3936
Epoch [2100/20000], Loss: 0.3812
Epoch [2200/20000], Loss: 0.3696
Epoch [2300/20000], Loss: 0.3586
Epoch [2400/20000], Loss: 0.3482
Epoch [2500/20000], Loss: 0.3382
...
Epoch [19800/20000], Loss: 0.0626
Epoch [19900/20000], Loss: 0.0625
Epoch [20000/20000], Loss: 0.0624
Training time: 8.62 seconds优化后发现确实效果好,近乎和用cpu训练的时长差不多。所以可以理解为数据从gpu到cpu的传输占用了大量时间。
下面尝试下第二个思路:
import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler
import time
import matplotlib.pyplot as plt# 设置GPU设备
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(f"使用设备: {device}")# 加载鸢尾花数据集
iris = load_iris()
X = iris.data # 特征数据
y = iris.target # 标签数据# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 归一化数据
scaler = MinMaxScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.transform(X_test)# 将数据转换为PyTorch张量并移至GPU
X_train = torch.FloatTensor(X_train).to(device)
y_train = torch.LongTensor(y_train).to(device)
X_test = torch.FloatTensor(X_test).to(device)
y_test = torch.LongTensor(y_test).to(device)class MLP(nn.Module):def __init__(self):super(MLP, self).__init__()self.fc1 = nn.Linear(4, 10) # 输入层到隐藏层self.relu = nn.ReLU()self.fc2 = nn.Linear(10, 3) # 隐藏层到输出层def forward(self, x):out = self.fc1(x)out = self.relu(out)out = self.fc2(out)return out# 实例化模型并移至GPU
model = MLP().to(device)# 分类问题使用交叉熵损失函数
criterion = nn.CrossEntropyLoss()# 使用随机梯度下降优化器
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 20000 # 训练的轮数# 用于存储每100个epoch的损失值和对应的epoch数
losses = []start_time = time.time() # 记录开始时间for epoch in range(num_epochs):# 前向传播outputs = model(X_train) # 隐式调用forward函数loss = criterion(outputs, y_train)# 反向传播和优化optimizer.zero_grad()loss.backward()optimizer.step()# 记录损失值if (epoch + 1) % 200 == 0:losses.append(loss.item()) # item()方法返回一个Python数值,loss是一个标量张量print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')# 打印训练信息if (epoch + 1) % 100 == 0: # range是从0开始,所以epoch+1是从当前epoch开始,每100个epoch打印一次print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')time_all = time.time() - start_time # 计算训练时间
print(f'Training time: {time_all:.2f} seconds')# 可视化损失曲线
plt.plot(range(len(losses)), losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss over Epochs')
plt.show()使用设备: cuda:0
Epoch [100/20000], Loss: 0.9757
Epoch [200/20000], Loss: 0.9060
Epoch [200/20000], Loss: 0.9060
Epoch [300/20000], Loss: 0.8385
Epoch [400/20000], Loss: 0.7701
Epoch [400/20000], Loss: 0.7701
Epoch [500/20000], Loss: 0.7053
Epoch [600/20000], Loss: 0.6479
Epoch [600/20000], Loss: 0.6479
Epoch [700/20000], Loss: 0.5996
Epoch [800/20000], Loss: 0.5598
Epoch [800/20000], Loss: 0.5598
Epoch [900/20000], Loss: 0.5269
Epoch [1000/20000], Loss: 0.4994
Epoch [1000/20000], Loss: 0.4994
Epoch [1100/20000], Loss: 0.4760
Epoch [1200/20000], Loss: 0.4555
Epoch [1200/20000], Loss: 0.4555
Epoch [1300/20000], Loss: 0.4373
Epoch [1400/20000], Loss: 0.4207
Epoch [1400/20000], Loss: 0.4207
Epoch [1500/20000], Loss: 0.4054
Epoch [1600/20000], Loss: 0.3912
Epoch [1600/20000], Loss: 0.3912
...
Epoch [19900/20000], Loss: 0.0615
Epoch [20000/20000], Loss: 0.0614
Epoch [20000/20000], Loss: 0.0614
Training time: 10.93 seconds
_call_方法
# 不带参数的call方法
class Counter:def __init__(self):self.count = 0def __call__(self):self.count += 1return self.count# 使用示例
counter = Counter()
print(counter()) # 输出: 1
print(counter()) # 输出: 2
print(counter.count) # 输出: 21
2
2# 带参数的call方法
class Adder:def __call__(self, a, b):print("唱跳篮球rap")return a + badder = Adder()
print(adder(3, 5)) # 输出: 8唱跳篮球rap
8作业
记录次数与剩余时长之间无明显线性关系,可能是因为:
训练的核心耗时在 GPU:模型的前向传播、反向传播、参数更新等操作均在 GPU 上完成,这些计算耗时占据总时间的 99% 以上。
记录操作在 CPU 执行:loss.item()、print()、losses.append()等记录操作由 CPU 处理,而 CPU 与 GPU 可并行工作。因此,记录操作的耗时不会阻塞 GPU 计算,仅增加少量 CPU 开销,对总时长影响微乎其微。
若假设 “记录次数与剩余时长成正比”,需满足:
1.每次记录的耗时固定且显著;
2.记录操作与 GPU 计算完全串行(即 CPU 等待 GPU 完成后再执行记录)。
但在实际场景中,GPU 与 CPU 异步并行打破了这一假设,导致剩余时长(即记录总耗时)与记录次数无严格线性关联。
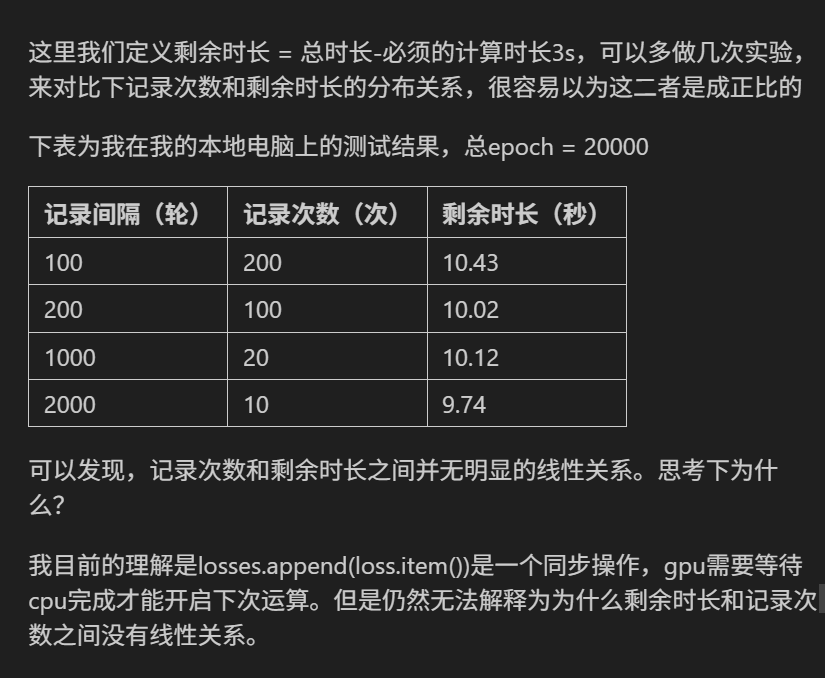
从实验数据看,不同记录间隔下的剩余时长差异极小(约 ±0.7 秒),且无单调趋势,这恰恰印证了记录操作的耗时可忽略且与 GPU 计算解耦。因此,在深度学习训练中,记录频率对总时长的影响几乎可以忽略,无需为减少耗时而刻意增大记录间隔(除非记录次数极多,如百万次)。
@浙大疏锦行
