当前位置： 首页 > news >正文

机器学习-特征工程

news 来源：原创 2025/5/17 8:27:38

一、概念

        特征工程：就是对特征进行相关处理。

        简单理解：有时候我们的数据来源不全是我们想要的数字（可能这些数据是文本、图像），我们需要将这些数据转化为用于机器学习的数字特征。此时就需要用到特征工程进行转换。

二、API

1.实例化转换器对象（工具）

  • 字典特征提取：DictVectorizer
  • 文本特征提取：CountVectorizer
  • TF-IDF文本特征词的重要程度特征提取：TfidfVectorizer
  • 归一化：MinMaxScaler
  • 标准化：StandarScaler
  • 低方差过滤：VarianceThreshold
  • 主成分分析：PCA

2.转换器方法（工具调用）

        转换器对象调用fit_transfrom()进行转换，这可以分开写，也可以一次搞定。

data_to = a.fit_transform(data)#等价于a.fit(data)
data_to = a.transform(data)#这里的a通常指的是一个数据转换器对象（实例化转换器对象）

其中：

        fit用于计算数据（训练），transform用于最终转换。

注意：在之后的代码实现中，调用之前已经训练好的数据时，不用在fit一次，直接transform就好。

三、字典列表特征提取

1.稀疏矩阵

        在讲解之前，要提一下稀疏矩阵（计算机常用）的概念：稀疏矩阵就是零元素远多于非零元素的矩阵。由于稀疏矩阵中零元素非常多，存储和处理稀疏矩阵时，通常会采用特殊的存储格式，以节省内存空间并提高计算效率。

        简单提及一下稠密矩阵：稠密矩阵（数学常用），是指矩阵中非零元素的数量与总元素数量相比接近或相等，也就是说矩阵中的大部分元素都是非零的。

        稀疏矩阵常见于大规模数据分析、图形学、自然语言处理(NLP)、机器学习等领域，而稠密矩阵在数学计算、线性代数等通用计算领域更为常见。

2.三元组表

        三元组表也是稀疏矩阵的类型数据，与稀疏矩阵不同的是，稀疏矩阵零元素多，三元组表存储的是非零元素的行列索引和值。   （行，列）数据

3.API

(1)sklearn.feature_extraction.DictVectorizer(spare=True)

  • sparse=True返回类型为csr_matrix的稀疏矩阵,稀疏矩阵可以调用.toarray()方法将稀疏矩阵转换为数组;
  • sparse=False表示返回的是数组.

(2)fit_transform(原数据data)

        转换器对象调用该方法，返回得到转换后的矩阵或数组

(3)get_feature_names_out()

        获取特征名

4.代码实现

注意：与pandas联用，df中data_to只能是密集矩阵，不能是稀疏矩阵。即sparse必须等于False，或者将稀疏矩阵转为数组后再联用。

（1）将数据提取为稀疏矩阵

from sklearn.feature_extraction import DictVectorizer
import pandas as pd
data = [{'city':'成都', 'age':30, 'temperature':20}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80},{'city':'上海', 'age':22, 'temperature':70},{'city':'成都', 'age':72, 'temperature':40},]
#实例化转换器对象（工具）
transfer = DictVectorizer(sparse=True)
#调用方法
data_to = transfer.fit_transform(data)
print('转换后的稀疏矩阵为：',data_to)
print('特征名：',transfer.get_feature_names_out())

结果：

（2）将数据提取为稀疏矩阵对应的数组

        两种方法：sparse=False，data_to.toarray()

i.spare方法：

from sklearn.feature_extraction import DictVectorizer
import pandas as pddata = [{'city':'成都', 'age':30, 'temperature':20}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80},{'city':'上海', 'age':22, 'temperature':70},{'city':'成都', 'age':72, 'temperature':40},]
transfer = DictVectorizer(sparse=False)
data_to = transfer.fit_transform(data)
print('转换为数组：',data_to)
# pd.DataFrame 无法直接接受稀疏矩阵作为输入
df = pd.DataFrame(data_to,columns=transfer.get_feature_names_out())
print(df)

结果：

转换为数组： [[30.  0.  0.  1.  0. 20.]
 [33.  0.  0.  0.  1. 60.]
 [42.  0.  1.  0.  0. 80.]
 [22.  1.  0.  0.  0. 70.]
 [72.  0.  0.  1.  0. 40.]]
    age  city=上海  city=北京  city=成都  city=重庆  temperature
0  30.0      0.0      0.0      1.0      0.0         20.0
1  33.0      0.0      0.0      0.0      1.0         60.0
2  42.0      0.0      1.0      0.0      0.0         80.0
3  22.0      1.0      0.0      0.0      0.0         70.0
4  72.0      0.0      0.0      1.0      0.0         40.0

 ii.toarray方法：

from sklearn.feature_extraction import DictVectorizer
data =  [{'city':'成都', 'age':30, 'temperature':20}, {'city':'重庆','age':33, 'temperature':60}, {'city':'北京', 'age':42, 'temperature':80},{'city':'上海', 'age':22, 'temperature':70},{'city':'成都', 'age':72, 'temperature':40},]
#创建转换器工具
transfer = DictVectorizer(sparse=True)
#调用方法
transfer.fit(data) #计算
data_to = transfer.transform(data) #转换
print(data_to.toarray())#三元组表转换为了数组

结果：

[[30.  0.  0.  1.  0. 20.]
 [33.  0.  0.  0.  1. 60.]
 [42.  0.  1.  0.  0. 80.]
 [22.  1.  0.  0.  0. 70.]
 [72.  0.  0.  1.  0. 40.]]

四、文本特征提取

1.API

        sklearn.featrue_extraction.text.CountVectorizer(stop_words)

stop_words:停止词，值为list，表示黑名单次，不纳入提取(统计)范围。

        fit_transform(data)

        jieba库（中文文本提取需要导入）安装指令：pip install jieba

2.代码实现

（1）英文文本提取

from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
data = ['i like lovely pappuy dog','do you like']
#创建实例化转化器对象（工具）
transfer = CountVectorizer(stop_words=['you'])
#调用方法
data_new = transfer.fit_transform(data)
print(data_new.toarray())
print(transfer.get_feature_names_out())df = pd.DataFrame(data_new.toarray(),columns=transfer.get_feature_names_out())
print(df)

结果：

[[0 1 1 1 1]
 [1 0 1 0 0]]
['do' 'dog' 'like' 'lovely' 'pappuy']
   do  dog  like  lovely  pappuy
     0   0    1     1       1       1
     1   1    0     1       0       0

注意：这段代码，没有把i显示出来。我并没有把i设为停止词，这是为什么？

原因：因为CountVectorizer默认配置会过滤掉单个字符的词汇。这是它的标准行为，与是否将 "i" 明确列为停用词无关。

如果想添加单个单词作为选词，可以采用这种修改方式，其他不用修改：

transfer = CountVectorizer(stop_words=['you'],token_pattern=r"(?u)\b\w+\b"  # 修改正则表达式，允许单字符词汇
)

（2）中文文本提取

from sklearn.feature_extraction.text import CountVectorizer
import jieba
data = ['今天不是星期四','今天是星期三','好好学习，天天向上']
#工具
transfer = CountVectorizer(stop_words=['天天'])
#转换
data_new = transfer.fit_transform(data)
print(data_new.toarray())
print(transfer.get_feature_names_out())

结果：

[[1 0 0 0]
 [0 1 0 0]
 [0 0 1 1]]
['今天不是星期四' '今天是星期三' '天天向上' '好好学习']

        可以发现这样的分词并不是我们想要的，因为python分词这个概念是国外先构思好的，英文本来就有空格分开，因此他们很快就可以分词。但是中文都是连在一起的，按着同样的方法，我们得到的是我们不想要的答案。

        此时我们就要用到jieba库：

from sklearn.feature_extraction.text import CountVectorizer
import jieba
import pandas as pd
data = '今天不是星期四,今天是星期三,好好学习，天天向上'
data = jieba.cut(data)
data = list(data)
print('我是分好的词语：',data)
#工具
transfer = CountVectorizer(stop_words=['天天'])
#转换
data_new = transfer.fit_transform(data)
print(data_new.toarray())
print(transfer.get_feature_names_out())
df = pd.DataFrame(data_new.toarray(),columns=transfer.get_feature_names_out())
print(df)

结果：

Building prefix dict from the default dictionary ...
Loading model from cache C:\WINDOWS\TEMP\jieba.cache
Loading model cost 0.618 seconds.
Prefix dict has been built successfully.
我是分好的词语： ['今天', '不是', '星期四', ',', '今天', '是', '星期三', ',', '好好学习', '，', '天天向上']  
[[0 1 0 0 0 0]
 [1 0 0 0 0 0]
 [0 0 0 0 0 1]
 [0 0 0 0 0 0]
 [0 1 0 0 0 0]
 [0 0 0 0 0 0]
 [0 0 0 0 1 0]
 [0 0 0 0 0 0]
 [0 0 0 1 0 0]
 [0 0 0 0 0 0]
 [0 0 1 0 0 0]]
['不是' '今天' '天天向上' '好好学习' '星期三' '星期四']
    不是  今天  天天向上  好好学习  星期三  星期四

 0    0   1     0     0    0    0

 1    1   0     0     0    0    0
 2    0   0     0     0    0    1
 3    0   0     0     0    0    0
 4    0   1     0     0    0    0
 5    0   0     0     0    0    0
 6    0   0     0     0    1    0
 7    0   0     0     0    0    0
 8    0   0     0     1    0    0
 9    0   0     0     0    0    0
10   0   0     1     0    0    0

 上面这种data赋值是直接设为字符串，正常情况下我们用的格式都和前面的差不多，data为列表，所以需要一个更完美的答案，将分词用.append方法连接，连成字符串，或者用列表推导式

data_new = []
for sentence in data:words = jieba.cut(sentence)data_new.append(list(words))
data_new = [list(jieba.cut(sentence)) for sentence in data]

其实也就多了一步：

from sklearn.feature_extraction.text import CountVectorizer
import jieba
import pandas as pd
data = ['今天不是星期四','今天是星期三','玉汝于成','开心小狗']
data_new = []
for sentence in data:words = jieba.cut(sentence)data_new.append(' '.join(words))
print('我是分好的词语：',data_new)
#工具
transfer = CountVectorizer(stop_words=['天天'])
#转换
data_final = transfer.fit_transform(data_new)
df = pd.DataFrame(data_final.toarray(),columns=transfer.get_feature_names_out())
print(df)

结果：

五、TF-IDF

1.概念

        TF：词频，这个词在文章里出现的频率。

        TF=某词在文章的出现次数/文章的总词数

在 TfidfVectorizer 中，TF 默认是：直接使用一个词在文档中出现的次数也就是CountVectorizer的结果，不用除以分母。

        IDF：逆文档频率，反应这个词在整个文档集合中的稀有程度。

        IDF=log(总文档数/包含某词的文档数+1)----这里加1是防止分母为0.

在 TfidfVectorizer 中，IDF 的默认计算公式是：

简单理解：

  • 如果一个词在很多文档中都出现，它的 IDF 值就低（说明这个词很 普通，如 “的”“是”）；反之 IDF 值高（说明这个词更 独特，如 “人工智能”）。

  • TF-IDF = TF × IDF：
    综合考虑词在单个文档中的频率和在整个集合中的稀有性

2.API

        sklearn.feature_extraction.text.TfidfVectorizer(stop_words)

        data_new = fit_transfrom(data)---返回稀疏矩阵

3.代码实现

import jieba
from sklearn.feature_extraction.text import TfidfVectorizer
data = ['今天星期四','明天星期五','后天周末','周末可以玩']
data_new = []
for word in data: # 遍历每个句子words = jieba.cut(word) #传入单个句子data_new.append(' '.join(words))
print('分词后的文本：',data_new,'-------')
#创建工具
transfer = TfidfVectorizer(stop_words=['周末'])
#调用工具
data_final = transfer.fit_transform(data_new)
print(transfer.get_feature_names_out())
print(data_final.toarray())

结果：

六、无量纲化

1.概念

        量纲即单位，无量纲化就是把原本有单位，不在一个量纲的数据进行统一规定，让它们都变成没有单位的数据。这样处理后的数据更统一，更好继续后续操作。

2.MInMaxScaler归一化

        通过对原始数据进行变换把数据映射到指定区间（默认为0-1）

        2.1公式

                

                 𝑥是当前特征值，𝑥scaled 是归一化后的特征值。

        2.2API

                sklearn.preprocessing.MinMaxScaler(feature_range)

                feature_range=(0,1) 归一化后的值域,可以自己设定

                fit_transform(data)

        2.3代码实现

原始数据为list:（一列数据看为一组）

from sklearn.preprocessing import MinMaxScaler
data = [[10,20,30],[40,50,60],[70,80,90]]
#创建工具
scaler = MinMaxScaler(feature_range=(0,1))
#计算，训练
scaler.fit(data)
#转换
data_new = scaler.transform(data)
print("最大最小归一化后的数据为:",data_new)

结果：

结果分析

  • 每列独立缩放：MinMaxScaler对每列单独计算最大最小值，因此各列的缩放比例可能不同。
  • 单调性保持：归一化后的数据保留了原始数据的顺序关系（如40在第一列中位于中间，归一化后仍为0.5）。
  • 特征范围统一：所有特征被缩放到相同区间，这对某些机器学习算法（如神经网络、K 近邻）很重要，可避免因特征尺度差异导致的权重分配不均。

验证示例

以第一列[10, 40, 70]为例：

  • 最小值 = 10，最大值 = 70
  • 归一化计算：
    • (10−10)/(70−10)=0
    • (40−10)/(70−10)=0.5
    • (70−10)/(70−10)=1

原始数据为DataFrame:

from sklearn.preprocessing import MinMaxScaler
import pandas as pd
data = [[10,20,30],[40,50,60],[70,80,90]]
df = pd.DataFrame(data,index = ['a','b','c'],columns=['x','y','z'])
print(df)
#创建工具
scaler = MinMaxScaler(feature_range=(1,2))
#计算，训练
scaler.fit(data)
#转换
data_new = scaler.transform(data)
print("最大最小归一化后的数据为:",data_new)

结果：

原始数据为ndarray:

from sklearn.preprocessing import MinMaxScaler
from sklearn.feature_extraction import DictVectorizer
import pandas as pd
data = [{'city':'成都', 'age':30, 'temperature':200},{'city':'重庆','age':33, 'temperature':60},{'city':'北京', 'age':42, 'temperature':80}]
#创建工具
transfer = DictVectorizer(sparse=False)#sparse=False表示不稀疏
#计算，训练
data_new = transfer.fit_transform(data)
print(transfer.get_feature_names_out())
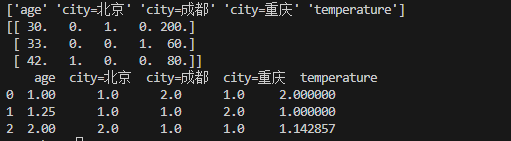
print(data_new)#创建工具
scaler = MinMaxScaler(feature_range=(1,2))#计算，训练
data_final = scaler.fit_transform(data_new)
df = pd.DataFrame(data_final,columns=transfer.get_feature_names_out())
print(df)

结果：

3.normalize归一化

API：from sklearn.preprocessing import normalize

                          normalize(data,norm=' ',axis=1)

                #data是要归一化的数据
                #norm是使用那种归一化:"l1"  "l2"  "max
                #axis=0是列  axis=1是行

        3.1 L1归一化--曼哈顿

from sklearn.preprocessing import normalize
data = [[1,2,0,2],[8,9,5,3],[6,4,7,1]]
result = normalize(data,norm='l1',axis=1)
print(result)

结果：

        3.2 L2归一化--欧氏距离

from sklearn.preprocessing import normalize
data = [[1,2,0,2],[8,9,5,3],[6,4,7,1]]
result = normalize(data,norm='l2',axis=1)
print(result)

结果：

        3.3 max归一化

from sklearn.preprocessing import normalize
data = [[1,2,0,2],[8,9,5,3],[6,4,7,1]]
result = normalize(data,norm='max',axis=1)
print(result)

结果：

4.StandardScaler标准化  

        4.1 公式

                就是正态分布的公式：

        4.2 API

               (1) sklearn.preprocessing.StandardScale

                与MinMaxScaler一样，原始数据类型可以是list、DataFrame和ndarray

                (2)fit_transform(data)

        4.3 代码实现

                

from sklearn.preprocessing import StandardScaler
data = [[1,2,0,2],[8,9,5,3],[6,4,7,1]]
scaler = StandardScaler()
data_new = scaler.fit_transform(data)
print(data_new)data2 = [[33,4,5,56],[67,23,45,7],[0,9,7,8]]
data2_new = scaler.transform(data2)
print(data2_new)

                结果：

利用data的工具直接转换data2标准化的结果。就不用再重新计算。

七、特征降维

        目的：降低特征维度，提高速度，降低计算成本，保留有关信息。

7.1 特征选择

解释：从原始特征集中挑选出最相关的特征。

        7.1.1 低方差过滤特征选择

                理解：如果一个特征的方差很小，说明这个特征的值在样本中几乎相同或区分不大，此时模型很难找到规律，这个特征相差不大就可以去掉。

                （1）API

                        sklearn.feature_selection.VarianceThreshold(threshold=2.0):创建对象，准备把方差为等于小于2的去掉，threshold的缺省值为2.0

                        transfer.fit_transform(data):把data中低方差特征去掉, data的类型可以是DataFrame、ndarray和list

                （2）代码实现
from sklearn.feature_selection import VarianceThreshold
import pandas as pd
def variance():data = pd.DataFrame([[10,1000],[11,3],[11,13],[11,50],[11,90],[11,32],[11,12],[11,61]])transfer = VarianceThreshold(threshold=3)data_new = transfer.fit_transform(data)df = pd.DataFrame(data_new)print(df)if __name__=='__main__':variance()

结果：

      0
0  1000
1     3
2    13
3    50
4    90
5    32
6    12
7    61

        7.1.2根据相关系数的特征选择

        利用相关系数衡量特征与目标变量间线性相关程度，留下相关性高的特征，筛除相关性低的，以优化模型。        

        皮尔逊相关系数：衡量两个连续变量的线性关系，取值 -1 到 1 。等于 1 是完全正相关，-1 是完全负相关，0 表示无线性相关 。

        人为确定一个阈值，用以判断相关系数的显著程度。比如设阈值为 0.3 ，表示只关注与目标变量相关性强于 0.3（绝对值）的特征。   

        （1）API

                scipy.stats.personr(x,y):计算x,y两特征之间的相关性

                返回对象有两个属性:

                statistic皮尔逊相关系数[-1,1]

                pvalue零假设(了解),统计上评估两个变量之间的相关性,越小越相关

        （2）代码实现
from scipy.stats import pearsonr
import pandas as pd
def variance():x = pd.DataFrame([[10,1000],[11,3],[11,13],[11,50]])y = pd.DataFrame([[100],[30],[130],[500]])res = pearsonr(x,y)   df = pd.DataFrame(res)print(df)print('皮尔逊相关系数：',res.statistic)print('零假设：',res.pvalue)if __name__=='__main__':variance()

结果：

         0         1
0  0.284534 -0.244693
1  0.715466  0.755307
皮尔逊相关系数： [ 0.28453386 -0.24469313]
零假设： [0.71546614 0.75530687]

7.2主成份分析（PCA）

解释：把之前的特征通过一系列数学计算，形成新的特征，新的特征数量小于之前的特征数量。

        7.2.1 原理--向量相乘，维度降低

                从原始特征空间中找到一个新的坐标系统，使得数据在新坐标轴上的投影能够最大程度地保留数据的方差，同时减少数据的维度。

                简单理解：

                你有一堆苹果，想挑几个最能代表所有苹果大小、颜色、甜度的 “典型苹果”。PCA 会先把苹果们的各种数据（比如尺寸、糖分）看成散点，然后画一条线，让所有点到这条线的投影最分散（代表最能区分苹果的特征），这是第一个 “典型”；再画一条垂直的线，找第二重要的特征，以此类推。
                最后用这几个 “典型” 代替所有苹果的数据，扔掉没用的细节，用更少的指标看懂全部苹果。

        7.2.2 步骤

              

        7.2.3API

                from sklearn.decomposition import PCA

                PCA(n_components=None)

  • 参数解释：    n_components:

    • 实参为小数时：表示降维后保留百分之多少的信息，系统也不知道降到几维，但是信息保留一定保留指定百分比。

    • from sklearn.decomposition import PCA
import numpy as np
#创建随机数组，元素范围为0-19，数组为五行四列
arr = np.random.randint(0,20,size=(5,4))
print(arr)
#创建工具
pca = PCA(n_components=0.9)
#调用工具
pca.fit(arr)
arr_new = pca.transform(arr)
print(arr_new)

      结果：

    • 可以观察到：原本五行四列的数组变为五行三列，特征还是少了一维的。达到了降维效果。

    • 实参为整数时：表示减少到多少特征

    • from sklearn.decomposition import PCA
import numpy as np
arr = np.random.randint(0,20,size=(5,4))
print(arr)
#创建工具
pca = PCA(n_components=2)
#调用工具
pca.fit(arr)
arr_new = pca.transform(arr)
print(arr_new)

  • 结果：

  • 可以观察到：原本五行四列的数组变为五行二列，特征少了两维，达到了降维效果。

  • 信息保留比=保留信息/原始信息。

相关文章：

  • GD32 GPIO失控的解决方案
  • 【动态导通电阻】GaN HEMT动态导通电阻的精确测量
  • 每日Prompt：迷你 3D 建筑
  • 【leetcode】94. 二叉树的中序遍历
  • 【技术原理】ELK技术栈的历史沿革与技术演进
  • 《Elasticsearch 源码解析与优化实战》笔记
  • 前端面经 9 JS中的继承
  • FC7300 WDG MCAL 配置引导
  • kubernetes的service与服务发现
  • 矩阵转置的LATEX写法
  • Spring Cloud深度实践：从服务发现到弹性智能API网关全景解析
  • import pywinauto后tkinter.filedialog.askdirectory()无法调用，直接卡死，应如何解决
  • 基于Matlab实现图像透明叠加程序
  • LED接口设计
  • 物联网设备远程管理：基于代理IP的安全固件更新通道方案
  • ChatGPT到Claude全适配：跨模型Prompt高级设计规范与迁移技巧
  • Python连接redis
  • 深入理解 JavaScript 事件循环机制
  • 【嵌入式开发-RGB 全彩 LED】
  • Nginx模块配置与请求处理详解
  • 中国新闻发言人论坛在京举行，郭嘉昆：让中国声音抢占第一落点
  • 昔日千亿房企祥生集团约2.03亿元债权被拍卖，起拍价8000万元
  • 悬疑剧背后的女编剧：创作的差异不在性别，而在经验
  • 泽连斯基：乌代表团已启程，谈判可能于今晚或明天举行
  • 北方产粮大省遭遇气象干旱，夏粮用水如何解决？
  • 绿景中国地产：洛杉矶酒店出售事项未能及时披露纯属疏忽，已采取补救措施