抛物线法(二次插值法)
抛物线法简介
抛物线法(Quadratic Interpolation Method)是一种用于一维单峰函数极值搜索的经典优化方法。该方法通过在区间内选取三个不同的点,拟合一条二次抛物线,并求取这条抛物线的极值点作为新的迭代点,从而逐步逼近函数的极值。它相比于0.618法或黄金分割法,具有更快的收敛速度,特别是在极值点附近表现出超线性收敛特性。
数学推导
设 f ( x ) f(x) f(x) 在区间 内有单个极值点,选取不同的点 ( x 1 , f ( x 1 ) ) (x_1, f(x_1)) (x1,f(x1)), ( x 2 , f ( x 2 ) ) (x_2, f(x_2)) (x2,f(x2)), ( x 3 , f ( x 3 ) ) (x_3, f(x_3)) (x3,f(x3)), 用它们你和出一条二次抛物曲线
f ( x ) = A x 2 + B x + C f(x) = Ax^2 + Bx + C f(x)=Ax2+Bx+C
根据三点插值法,可以推导出抛物线极值点的公式
x m i n = f ( x 1 ) ( x 2 2 − x 3 2 ) + f ( x 2 ) ( x 3 2 − x 1 2 ) + f ( x 3 ) ( x 1 2 − x 2 2 ) 2 [ f ( x 1 ) ( x 2 − x 3 ) + f ( x 2 ) ( x 3 − x 1 ) + f ( x 3 ) ( x 1 − x 2 ) ] x_{min} = \frac{f(x_1) (x_2^2 -x_3^2) + f(x_2) (x_3^2 - x_1^2) + f(x_3)(x_1^2 -x_2^2)}{ 2[f(x_1)(x_2 - x_3) + f(x_2)(x_3 - x_1) + f(x_3)(x_1 - x_2)]} xmin=2[f(x1)(x2−x3)+f(x2)(x3−x1)+f(x3)(x1−x2)]f(x1)(x22−x32)+f(x2)(x32−x12)+f(x3)(x12−x22)
这个公式直接给出了二次曲线顶点的位置,作为当前迭代中的极小值近似。
算法流程
-
选取初始区间 [ a , b ] [a, b] [a,b] 内的三个点 x 1 x_1 x1, x 2 x_2 x2, x 3 x_3 x3
这三个点一般选取为 x 1 = a x_1 = a x1=a, x 3 = b x_3 = b x3=b, x 2 = a + b 2 x_2 = \frac{a+b}{2} x2=2a+b, 设定容许误差 η \eta η -
计算函数值 f ( x 1 ) f(x_1) f(x1), f ( x 2 ) f(x_2) f(x2) 和 f ( x 3 ) f(x_3) f(x3)
-
拟合抛物线,计算顶点 根据三点插值公式,拟合出二次函数,并计算顶点坐标:
x m i n = f ( x 1 ) ( x 2 2 − x 3 2 ) + f ( x 2 ) ( x 3 2 − x 1 2 ) + f ( x 3 ) ( x 1 2 − x 2 2 ) 2 [ f ( x 1 ) ( x 2 − x 3 ) + f ( x 2 ) ( x 3 − x 1 ) + f ( x 3 ) ( x 1 − x 2 ) ] x_{min} = \frac{f(x_1) (x_2^2 -x_3^2) + f(x_2) (x_3^2 - x_1^2) + f(x_3)(x_1^2 -x_2^2)}{ 2[f(x_1)(x_2 - x_3) + f(x_2)(x_3 - x_1) + f(x_3)(x_1 - x_2)]} xmin=2[f(x1)(x2−x3)+f(x2)(x3−x1)+f(x3)(x1−x2)]f(x1)(x22−x32)+f(x2)(x32−x12)+f(x3)(x12−x22) -
判断是否满足精度要求 η \eta η
如果
∣ x m i n − x 2 ∣ < η |x_{min} - x_2| < \eta ∣xmin−x2∣<η
说明收敛,极小值点为 x min x_{\text{min}} xmin,停止迭代。 -
根据极值点位置和函数值更新三个点
计算 f min = f ( x min ) f_{\text{min}} = f(x_{\text{min}}) fmin=f(xmin)
比较 x min x_{\text{min}} xmin 和 x 2 x_2 x2,分情况更新
| 情况 | 条件 | 更新方式 |
|---|---|---|
| A | x min < x 2 x_{\text{min}} < x_2 xmin<x2 且 f min < f 2 f_{\text{min}} < f_2 fmin<f2 | x 3 ← x 2 x_3 \leftarrow x_2 x3←x2, f 3 ← f 2 f_3 \leftarrow f_2 f3←f2 x 2 ← x min x_2 \leftarrow x_{\text{min}} x2←xmin, f 2 ← f min f_2 \leftarrow f_{\text{min}} f2←fmin |
| B | x min < x 2 x_{\text{min}} < x_2 xmin<x2 且 f min ≥ f 2 f_{\text{min}} \geq f_2 fmin≥f2 | x 1 ← x min x_1 \leftarrow x_{\text{min}} x1←xmin, f 1 ← f min f_1 \leftarrow f_{\text{min}} f1←fmin |
| C | x min > x 2 x_{\text{min}} > x_2 xmin>x2 且 f min < f 2 f_{\text{min}} < f_2 fmin<f2 | x 1 ← x 2 x_1 \leftarrow x_2 x1←x2, f 1 ← f 2 f_1 \leftarrow f_2 f1←f2 x 2 ← x min x_2 \leftarrow x_{\text{min}} x2←xmin, f 2 ← f min f_2 \leftarrow f_{\text{min}} f2←fmin |
| D | x min > x 2 x_{\text{min}} > x_2 xmin>x2 且 f min ≥ f 2 f_{\text{min}} \geq f_2 fmin≥f2 | x 3 ← x min x_3 \leftarrow x_{\text{min}} x3←xmin, f 3 ← f min f_3 \leftarrow f_{\text{min}} f3←fmin |
- 重复第 2 步到第 5 步, 直到收敛
当 ∣ x min − x 2 ∣ < η |x_{\text{min}} - x_2| < \eta ∣xmin−x2∣<η,返回 x min x_{\text{min}} xmin 作为极小值点
算法实现
#include <iostream>
#include <cmath>
#include <functional>
#include <algorithm>class QuadraticInterpolation {
private:double x1, x2, x3; // 三个采样点double eps; // 精度要求std::function<double(double)> func; // 待优化目标函数public:// 构造函数QuadraticInterpolation(double a, double b, double e, std::function<double(double)> f): x1(a), x2((a + b) / 2), x3(b), eps(e), func(f) {}// 执行搜索double search() {double f1 = func(x1);double f2 = func(x2);double f3 = func(x3);double xmin;while (true) {// 抛物线拟合顶点公式double numerator = f1 * (std::pow(x2, 2) - std::pow(x3, 2)) +f2 * (std::pow(x3, 2) - std::pow(x1, 2)) +f3 * (std::pow(x1, 2) - std::pow(x2, 2));double denominator = 2 * (f1 * (x2 - x3) +f2 * (x3 - x1) +f3 * (x1 - x2));if (std::abs(denominator) < 1e-12) break; // 防止除0异常xmin = numerator / denominator;double fmin = func(xmin);// 判断是否达到精度if (std::fabs(xmin - x2) < eps) break;// 更新三点,保留较优的三个点if (xmin < x2) {if (fmin < f2) {x3 = x2;f3 = f2;x2 = xmin;f2 = fmin;}else {x1 = xmin;f1 = fmin;}}else {if (fmin < f2) {x1 = x2;f1 = f2;x2 = xmin;f2 = fmin;}else {x3 = xmin;f3 = fmin;}}}return xmin;}
};// 示例函数
double testFunc(double x) {return x * x - sin(x);
}int main() {// 构造优化器,区间[0,5],精度1e-6QuadraticInterpolation optimizer(0, 1, 1e-6, testFunc);double result = optimizer.search();std::cout << "极小值点 x ≈ " << result << std::endl;std::cout << "对应的 f(x) ≈ " << testFunc(result) << std::endl;return 0;
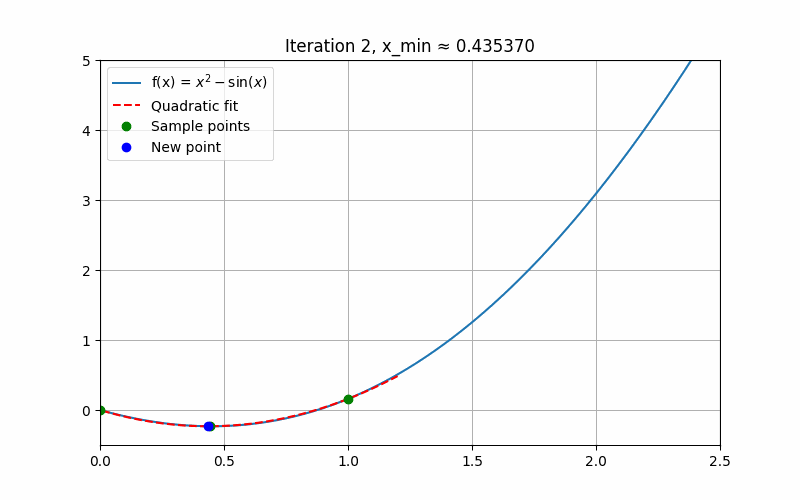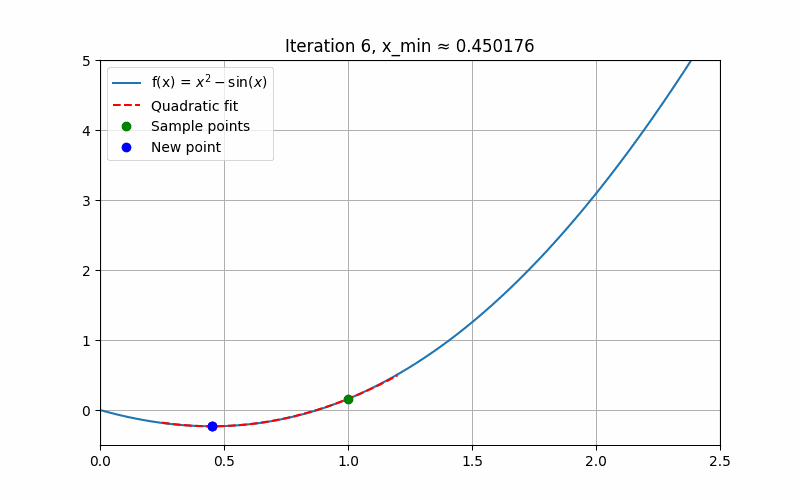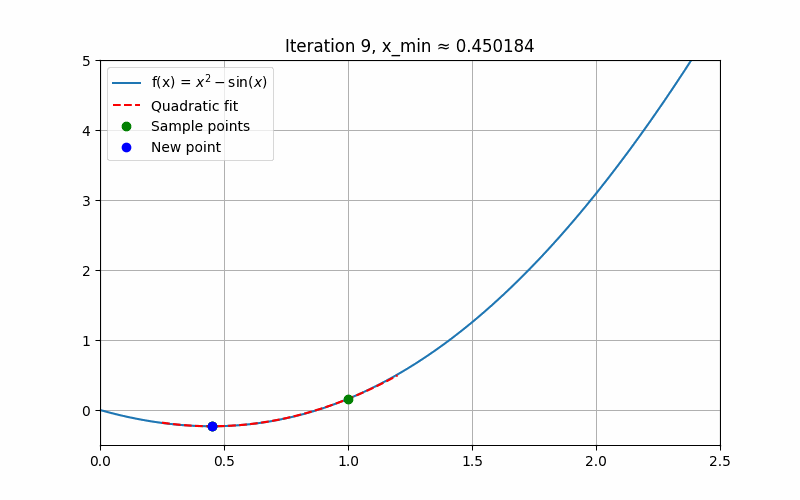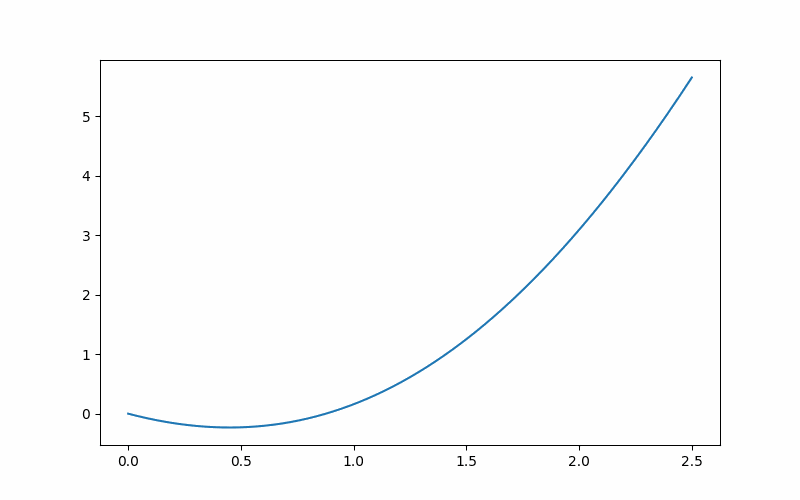
}
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation, PillowWriter# 定义目标函数
def f(x):return x**2 - np.sin(x)# 抛物线插值法计算顶点
def quadratic_interpolation(x1, x2, x3, f1, f2, f3):numerator = f1*(x2**2 - x3**2) + f2*(x3**2 - x1**2) + f3*(x1**2 - x2**2)denominator = 2*(f1*(x2 - x3) + f2*(x3 - x1) + f3*(x1 - x2))if np.abs(denominator) < 1e-12:return x2 # 防止除0return numerator / denominator# 初始参数
x1, x2, x3 = 0.0, 1.0, 2.0
eps = 1e-6# 函数取值范围
x_vals = np.linspace(0, 2.5, 400)
y_vals = f(x_vals)# 创建图形
fig, ax = plt.subplots(figsize=(8, 5))iteration = [0] # 用 list 包一层,方便闭包修改def update(_):global x1, x2, x3iteration[0] += 1ax.clear()ax.plot(x_vals, y_vals, label="f(x) = $x^2 - \sin(x)$")f1, f2, f3 = f(x1), f(x2), f(x3)# 防止三点重合if abs(x1 - x2) < 1e-10 or abs(x1 - x3) < 1e-10 or abs(x2 - x3) < 1e-10:ani.event_source.stop()return# 拟合抛物线 y = A x^2 + B x + CX = np.array([[x1**2, x1, 1],[x2**2, x2, 1],[x3**2, x3, 1]])Y = np.array([f1, f2, f3])try:coeffs = np.linalg.solve(X, Y)except np.linalg.LinAlgError:ani.event_source.stop()returnA, B, C = coeffs# 拟合抛物线曲线x_fit = np.linspace(min(x1, x2, x3)-0.2, max(x1, x2, x3)+0.2, 200)y_fit = A * x_fit**2 + B * x_fit + Cax.plot(x_fit, y_fit, 'r--', label="Quadratic fit")# 计算拟合顶点xmin = quadratic_interpolation(x1, x2, x3, f1, f2, f3)fmin = f(xmin)# 绘制采样点和拟合点ax.plot([x1, x2, x3], [f1, f2, f3], 'go', label="Sample points")ax.plot(xmin, fmin, 'bo', label="New point")# 显示当前迭代信息ax.set_title(f"Iteration {iteration[0]}, x_min ≈ {xmin:.6f}")# 判断收敛,满足条件则停止动画if np.abs(xmin - x2) < eps:ani.event_source.stop()# 更新三点if xmin < x2:if fmin < f2:x3, f3 = x2, f2x2, f2 = xmin, fminelse:x1, f1 = xmin, fminelse:if fmin < f2:x1, f1 = x2, f2x2, f2 = xmin, fminelse:x3, f3 = xmin, fminax.legend()ax.set_xlim(0, 2.5)ax.set_ylim(-0.5, 5)ax.grid(True)# 动画:frames 不设定固定值,interval 控控制刷新速度
ani = FuncAnimation(fig, update, interval=500, repeat=False)# 保存 GIF
ani.save("quadratic_interpolation_auto_stop.gif", writer=PillowWriter(fps=2))plt.show()