LeetCode105_从先序与中序遍历序列构造二叉树

标签：#树 #数组 #哈希表 #分治 #二叉树

Ⅰ. 题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

Ⅱ. 示例

· 示例 1:

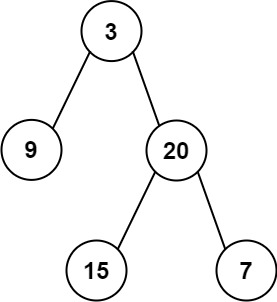
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

· 示例 2:
输入: preorder = [-1], inorder = [-1]
输出: [-1]

0. 个人方法

• 先序：即（根、左、右）的排列方式；
• 中序：即（左、根、右）的排列方式。

Q：要构造这颗二叉树，肯定要进行完整的遍历，那该如何遍历呢？
A：根结点肯定是一个重要的结点，我们可以以根结点为起点，通过递归，不断对左右子树进行搜索，并返回根结点，逐步构建成这颗二叉树。

1. 首先观察先序遍历：根结点始终在最前面（这很好，方便我们递归时对根结点的操作），但是左、右子树的边界在先序中不明显，那怎么办呢？
2. 这时我们再观察中序遍历：中序遍历中，根结点把左右子树分开了，所以我们可以通过在先序中得到的根结点，在中序遍历中找到它，这样就有左右子树的长度了，也可以返回去用到先序遍历中了。
3. 递归：观察完先序和中序后，递归的写法就很明了了。题目只给了调用两个根结点的函数，这显然是不够用的，因为我们要对左右子树进行操作，所以先定义一个新函数，在新函数中进行递归。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {return buildTreeRoot(preorder, 0, preorder.size()-1, inorder,  0, inorder.size()-1);}TreeNode* buildTreeRoot(vector<int>& preorder, int preStart, int preEnd,vector<int>& inorder,  int inStart,  int inEnd){// 0. 先写递归停止的条件if (preStart > preEnd || inStart > inEnd){return nullptr;}// 1. 从根结点开始，判断左右子树区间TreeNode* root = new TreeNode(preorder[preStart]);// 2. 找到中序遍历中的根结点int mid = 0;for (int i=inStart; i<=inEnd; i++){if (inorder[i] == preorder[preStart]){mid = i;break;}}// 3. 左子树的大小int leftsize = mid - inStart;root->left = buildTreeRoot(preorder, preStart+1, preStart+leftsize, inorder,  inStart,  mid-1);root->right = buildTreeRoot(preorder, preStart+leftsize+1, preEnd, inorder,  mid+1, inEnd);return root;}
};

• 复杂度分析

  • 时间复杂度：O(n)，其中 n 是树中的节点个数。

  • 空间复杂度：O(n)，除去返回的答案需要的 O(n) 空间之外，我们还需要使用 O(n) 的空间存储哈希映射，以及 O(h)（其中 h 是树的高度）的空间表示递归时栈空间。这里 h<n，所以总空间复杂度为 O(n)。

官方题解二：迭代

• 迭代法是一种非常巧妙的实现方法。

• 对于前序遍历中的任意两个连续节点 u 和 v，根据前序遍历的流程，我们可以知道 u 和 v 只有两种可能的关系：

  • v 是 u 的左儿子。这是因为在遍历到 u 之后，下一个遍历的节点就是 u 的左儿子，即 v；

  • u 没有左儿子，并且 v 是 u 的某个祖先节点（或者 u 本身）的右儿子。如果 u 没有左儿子，那么下一个遍历的节点就是 u 的右儿子。如果 u 没有右儿子，我们就会向上回溯，直到遇到第一个有右儿子（且 u 不在它的右儿子的子树中）的节点 u_a，那么 v 就是 u_a 的右儿子。

class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if (!preorder.size()) {return nullptr;}TreeNode* root = new TreeNode(preorder[0]);stack<TreeNode*> stk;stk.push(root);int inorderIndex = 0;for (int i = 1; i < preorder.size(); ++i) {int preorderVal = preorder[i];TreeNode* node = stk.top();if (node->val != inorder[inorderIndex]) {node->left = new TreeNode(preorderVal);stk.push(node->left);}else {while (!stk.empty() && stk.top()->val == inorder[inorderIndex]) {node = stk.top();stk.pop();++inorderIndex;}node->right = new TreeNode(preorderVal);stk.push(node->right);}}return root;}
};