二叉树 - JS - 2

一、递归问题的统一套路（4步法）

1. ​明确递归的定义（函数的作用）​​

• ​关键问题​：这个递归函数到底要完成什么任务？
• ​示例​：
  • 二叉树路径问题：dfs(node, path) 的作用是「记录从根到当前节点的路径」。
  • 斐波那契数列：fib(n) 的作用是「返回第 n 个斐波那契数」。

2. ​确定递归终止条件​

• ​原则​：在问题无法再分解（最小子问题）时终止。
• ​常见终止条件​：
  • 二叉树问题：if (node == null) return...
  • 数组/字符串问题：if (index >= length) return...
  • 数值问题：if (n == 0 || n == 1) return...

3. ​处理当前层逻辑​

• ​操作​：对当前数据做处理（如计算、选择、拼接等）。
• ​示例​：
  • 二叉树路径：path += node.val
  • 全排列问题：swap(nums[i], nums[start])

4. ​递推到下一层​

• ​缩小问题规模​：通过参数变化进入子问题。
• ​关键点​：
  • 参数如何传递？（如 dfs(node.left, path + "->")）
  • 是否需要回溯？（如组合问题要撤销选择）

二、二叉树操作

257.二叉树的所有路径

题目描述

257. 二叉树的所有路径

 

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

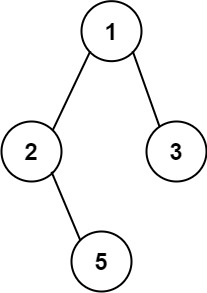
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]

提示：

• 树中节点的数目在范围 [1, 100] 内
• -100 <= Node.val <= 100

解题思路​

这道题可以使用 ​深度优先搜索（DFS）​​ 来遍历所有可能的路径。具体步骤如下：

1. ​递归遍历​：从根节点开始，递归访问左子树和右子树。
2. ​记录路径​：在递归过程中，维护当前路径的字符串。
3. ​到达叶子节点时保存路径​：当遇到叶子节点（没有左右子节点）时，将当前路径加入结果列表。

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {string[]}*/
var binaryTreePaths = function (root) {const paths = [];// 深度优先const dfs = (node, path) => {if (!node) return;// 当前节点加入路径path += node.val;// 如果是叶子节点，保存路径if (!node.left && !node.right) {paths.push(path);return;}// 继续递归左子树和右子树path += "->";dfs(node.left, path);dfs(node.right, path);};dfs(root, "");return paths;
}

 404.左叶子之和

题目描述

404. 左叶子之和

 

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

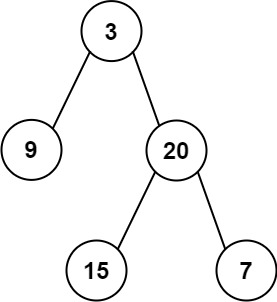
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0

提示:

• 节点数在 [1, 1000] 范围内
• -1000 <= Node.val <= 1000

解题思路​

1. ​识别左叶子节点​：
   • 必须是某个节点的左子节点。
   • 必须没有左右子节点​（即叶子节点）。
2. ​递归遍历​：
   • 检查当前节点的左子节点是否是叶子节点，如果是则累加其值。
   • 递归处理左子树和右子树。

/*** Definition for a binary tree node.* function TreeNode(val, left, right) {*     this.val = (val===undefined ? 0 : val)*     this.left = (left===undefined ? null : left)*     this.right = (right===undefined ? null : right)* }*/
/*** @param {TreeNode} root* @return {number}*/
var sumOfLeftLeaves = function (root) {if (!root) return 0;let sum = 0;// 检查左子节点是否是左叶子if (root.left && !root.left.left && !root.left.right) {sum += root.left.val;}// 递归处理左右子树sum += sumOfLeftLeaves(root.left);sum += sumOfLeftLeaves(root.right);return sum;
};