文献分享: Aligner——学习稀疏对齐的检索模型
文章目录
- 1. \textbf{1. } 1. 背景与导论
- 3. Aligner \textbf{3. Aligner} 3. Aligner原理
- 3.0. \textbf{3.0. } 3.0. 模型的假设
- 3.1. \textbf{3.1. } 3.1. 稀疏矩阵
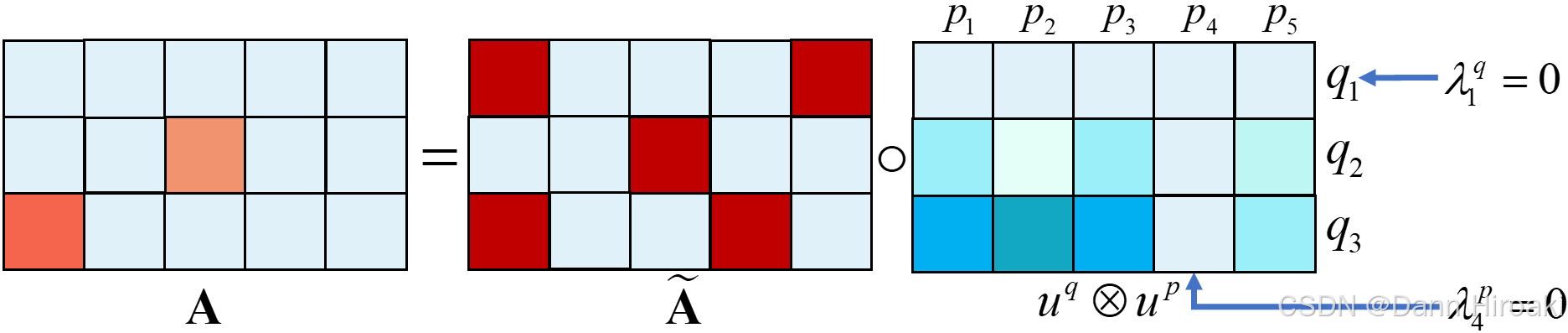
- 3.1.1. \textbf{3.1.1. } 3.1.1. 稀疏矩阵的分解 A = A ~ ∘ ( u q ⊗ u p ) ∈ R n × m \boldsymbol{\textbf{A}\text{=}\tilde{\textbf{A}}\text{∘}(u^q\text{⊗}u^p)\text{∈}\mathbb{R}^{n\text{×}m}} A=A~∘(uq⊗up)∈Rn×m
- 3.1.2. \textbf{3.1.2. } 3.1.2. 如何确定显著性矩阵 ( u q ⊗ u p ) \boldsymbol{(u^q\text{⊗}u^p)} (uq⊗up): 显著性参数的学习
- 3.1.3. \textbf{3.1.3. } 3.1.3. 如何确定稀疏性矩阵 A ~ \tilde{\textbf{A}} A~: 在小样本上的对齐适配
- 3.2. \textbf{3.2. } 3.2. 基于显著性的剪枝
- 4. \textbf{4. } 4. 实验概要
原文,另外这篇文章被 ICLR’23 \text{ICLR'23} ICLR’23拒稿了,公开处刑见 OpenReview \text{OpenReview} OpenReview(几个审稿人说的都挺好的)
1. \textbf{1. } 1. 背景与导论
1️⃣多向量文本检索的定义:给定一个查询 Q Q Q和一个包含 N N N个段落的段落集 P = { P ( 1 ) , P ( 2 ) , … , P ( N ) } \mathscr{P}\text{=}\left\{P^{(1)},P^{(2)},\ldots,P^{(N)}\right\} P={P(1),P(2),…,P(N)}
- 嵌入:为 Q Q Q与 P = { P ( 1 ) , P ( 2 ) , … , P ( N ) } \mathscr{P}\text{=}\left\{P^{(1)},P^{(2)},\ldots,P^{(N)}\right\} P={P(1),P(2),…,P(N)}的每个 Token \text{Token} Token都生成一向量,即 Q = { q 1 , q 2 , … , q n } Q\text{=}\left\{q_{1},q_2,\ldots,q_{n}\right\} Q={q1,q2,…,qn}和 P ( j ) = { p 1 ( j ) , p 2 ( j ) , … , p m ( j ) } P^{(j)}\text{=}\{p_{1}^{(j)},p_{2}^{(j)},\ldots,p_{m}^{(j)}\} P(j)={p1(j),p2(j),…,pm(j)}
- 检索:让每个 q i ∈ Q q_i\text{∈}Q qi∈Q在所有段落子向量集 P ( 1 ) ∪ P ( 2 ) ∪ … ∪ P ( N ) P^{(1)}\text{∪}P^{(2)}\text{∪}\ldots\text{∪}P^{(N)} P(1)∪P(2)∪…∪P(N)中执行 MIPS \text{MIPS} MIPS(最大内积搜索),得到 Top- K \text{Top-}K Top-K的段落子向量
- 回溯:合并 n n n个 q i q_i qi的 MIPS \text{MIPS} MIPS结果得到 n × K n\text{×}K n×K个段落子向量,将每个子向量回溯到其所属段落得到 P ′ = { P ( 1 ) , P ( 2 ) , … , P ( M ) } \mathscr{P}^\prime\text{=}\left\{P^{(1)},P^{(2)},\ldots,P^{(M)}\right\} P′={P(1),P(2),…,P(M)}
- 重排:用基于 MaxSim \text{MaxSim} MaxSim的后期交互计算精确相似度评分 ( Q , P ) = ∑ i = 1 n max j = 1 … m q i ⊤ p j \displaystyle{}(Q,P)\text{=}\sum_{i=1}^{n} \max _{j=1 \ldots m} q_{i}^{\top} p_{j} (Q,P)=i=1∑nj=1…mmaxqi⊤pj,从而对 P ′ \mathscr{P}^\prime P′进行重排得到最相似段落
2️⃣ ColBERT \text{ColBERT} ColBERT中 MaxSim \text{MaxSim} MaxSim的缺陷
- 检索性能上: MaxSim \text{MaxSim} MaxSim操作为每个查询向量 q i q_i qi找到单个段落向量 p q i p_{q_i} pqi,放宽单个的约束可能可以提升检索性能
- 检索效率上:在检索阶段,传统的 ColBERT \text{ColBERT} ColBERT并不会对向量个数 ∣ P ∣ |P| ∣P∣进行剪枝,但存储计算开销 ∝ ∣ P ∣ \text{∝}|P| ∝∣P∣
2️⃣改进的直觉:引入稀疏矩阵 A \textbf{A} A来扩展原有的 MaxSim \text{MaxSim} MaxSim操作
- 数据结构:相似度矩阵 S \textbf{S} S,和稀疏矩阵 A \textbf{A} A
- 对于 S \textbf{S} S:令查询 Q = { q 1 , q 2 , … , q n } Q\text{=}\left\{q_{1},q_2,\ldots,q_{n}\right\} Q={q1,q2,…,qn}以及文档 P = { p 1 , p 2 , . . . , p m } P\text{=}\{p_1,p_2,...,p_m\} P={p1,p2,...,pm}中,记子内积为 s i j = q i ⊤ p j s_{ij}\text{=}{q}_{i}^{\top}{p}_{j} sij=qi⊤pj,由此构成 S ∈ R n × m \textbf{S}\text{∈}\mathbb{R}^{n\text{×}m} S∈Rn×m
- 对于 A \textbf{A} A:让每个元素 a i j ∈ [ 0 , 1 ] a_{ij}\text{∈}[0,1] aij∈[0,1]来对 S \textbf{S} S中的元素进行不同强度的选择,由此构成 A ∈ R n × m \textbf{A}\text{∈}\mathbb{R}^{n\text{×}m} A∈Rn×m
- 相似评分: Sim ( Q , D ) = 1 Z ∑ i = 1 n ∑ j = 1 m ( S ∘ A ) i j \displaystyle\text{Sim}(Q,D)\text{=}\frac{1}{Z} \sum_{i=1}^{n} \sum_{j=1}^{m}(\textbf{S}\text{∘}\textbf{A})_{ij} Sim(Q,D)=Z1i=1∑nj=1∑m(S∘A)ij
- S ∘ A \textbf{S}\text{∘}\textbf{A} S∘A表示两矩阵的 Hadamard \text{Hadamard} Hadamard积,即两形状相同的矩阵按位相乘,构成新的形状相同的矩阵
- ∑ i = 1 n ∑ j = 1 m ( S ∘ A ) i j \displaystyle\sum_{i=1}^{n} \sum_{j=1}^{m}(\textbf{S}\text{∘}\textbf{A})_{ij} i=1∑nj=1∑m(S∘A)ij表示将 S ∘ A \textbf{S}\text{∘}\textbf{A} S∘A矩阵的每位相加,最后再进行 Z Z Z归一化即除以 A \textbf{A} A中所有 m × n m\text{×}n m×n个元素的总和
- 对比:稠密检索和多向量检索,可以看出稀疏矩阵 A \textbf{A} A的特殊情况
- 稠密检索:计算 P P P和 Q Q Q嵌入后二者
<cls>的内积,相当于用 A \textbf{A} A屏蔽掉其它子向量的相似度
- 多向量检索:找到每个 q i q_i qi找到最相似的段落子向量 p p p,相当于设置 A \textbf{A} A以选取 S \textbf{S} S中每行最大元素
3. Aligner \textbf{3. Aligner} 3. Aligner原理
3.0. \textbf{3.0. } 3.0. 模型的假设
1️⃣不同任务有不同的最优对齐方式,例如
- 事实型:例如查询
Who-is-the-president-of-USA的答案通常集中在 P P P的某一部分,因此只需要少量且集中的对齐即可- 论点型:例如查询
Who-is-next-president-of-USA的答案需要综合多个文档 P P P进行分析,影刺需要较多且分散的对齐2️⃣一个段落 P P P中大多 Token \text{Token} Token不贡献语义
- 实验上:只有 1 / 10 1/10 1/10左右的文档在 MaxSim \text{MaxSim} MaxSim时被检索到过,即大多的 Token \text{Token} Token不具备检索的价值
- 如何作:可以对大多 Token \text{Token} Token进行剪枝
3.1. \textbf{3.1. } 3.1. 稀疏矩阵
3.1.1. \textbf{3.1.1. } 3.1.1. 稀疏矩阵的分解 A = A ~ ∘ ( u q ⊗ u p ) ∈ R n × m \boldsymbol{\textbf{A}\text{=}\tilde{\textbf{A}}\text{∘}(u^q\text{⊗}u^p)\text{∈}\mathbb{R}^{n\text{×}m}} A=A~∘(uq⊗up)∈Rn×m

数据结构 维度 范围 意义 稀疏性矩阵 A ~ ∈ R n × m \tilde{\textbf{A}}\text{∈}\mathbb{R}^{n\text{×}m} A~∈Rn×m a i j ∈ { 0 , 1 } a_{ij}\text{∈}\{0,1\} aij∈{0,1} a i j a_{ij} aij决定了 s i j = q i ⊤ p j s_{ij}\text{=}{q}_{i}^{\top}{p}_{j} sij=qi⊤pj是否参与最终评分 显著性向量 u q , u p ∈ R n u^q,u^p\text{∈}\mathbb{R}^{n} uq,up∈Rn u i q , u j p ∈ [ 0 , 1 ] u^q_{i},u^p_{j}\text{∈}[0,1] uiq,ujp∈[0,1] u i q / u j p u^q_{i}/u^p_{j} uiq/ujp相当于 q i / p j q_i/p_j qi/pj的一个重要性权重 显著性矩阵 ( u q ⊗ u p ) ∈ R n × m (u^q\text{⊗}u^p)\text{∈}\mathbb{R}^{n\text{×}m} (uq⊗up)∈Rn×m ( u q ⊗ u p ) i j = u i q u j p ∈ [ 0 , 1 ] (u^q\text{⊗}u^p)_{ij}\text{=}u^q_{i}u^p_{j}\text{∈}[0,1] (uq⊗up)ij=uiqujp∈[0,1] u i q u j p u^q_{i}u^p_{j} uiqujp决定了 s i j = q i ⊤ p j s_{ij}\text{=}{q}_{i}^{\top}{p}_{j} sij=qi⊤pj参与最终评分的权重 3.1.2. \textbf{3.1.2. } 3.1.2. 如何确定显著性矩阵 ( u q ⊗ u p ) \boldsymbol{(u^q\text{⊗}u^p)} (uq⊗up): 显著性参数的学习
1️⃣显著性的定义:以段落子向量 p i p_i pi为例,其显著性定义为 u i p = λ i p ×ReLU ( W p p i + b p ) u_{i}^{p}\text{=}\lambda_{i}^{p}\text{×ReLU}\left(\textbf{W}^{p} {p}_{i}\text{+}b^{p}\right) uip=λip×ReLU(Wppi+bp)
- 神经网络部分: ReLU ( W p p i + b p ) \text{ReLU}\left(\textbf{W}^{p}p_i \text{+}b^{p}\right) ReLU(Wppi+bp)为一前馈网络, W p \textbf{W}^{p} Wp和 b p b^{p} bp是可学习参数,最终给出 p i {p}_{i} pi一个显著性得分
- 稀疏性门控变量: λ i p ∈ [ 0 , 1 ] \lambda_{i}^{p}\text{∈}[0,1] λip∈[0,1]用于控制该 p i {p}_{i} pi被激活的程度,当 λ i p = 0 \lambda_{i}^{p}\text{=}0 λip=0时与 p i {p}_{i} pi有关的相似度全被屏蔽
2️⃣训练方法:基于熵正则化线性规划的训练
- 有关符号:令 s i p =ReLU ( W p p i + b p ) s_i^p\text{=ReLU}\left(\textbf{W}^{p} {p}_{i}\text{+}b^{p}\right) sip=ReLU(Wppi+bp)构成向量 s p = { s 1 p , s 2 p , . . . , s m p } s^p\text{=}\{s^p_1,s^p_2,...,s^p_m\} sp={s1p,s2p,...,smp},以及门控向量 λ p = { λ 1 p , λ 1 p , . . . , λ m p } {\lambda}^p\text{=}\{\lambda_{1}^{p},\lambda_{1}^{p},...,\lambda_{m}^{p}\} λp={λ1p,λ1p,...,λmp}
- 训练目标: max ⟨ s p , λ p ⟩ – ε ∑ i = 1 m λ p i log λ p i \displaystyle\max\langle{s^p,\lambda^p}\rangle\text{ – }\varepsilon{\mathop{\sum}\limits_{{i=1}}^{m}{\lambda^p}_{i}\log{\lambda^p}_{i}} max⟨sp,λp⟩ – εi=1∑mλpilogλpi,并约束 λ i p ∈ [ 0 , 1 ] \lambda_{i}^{p}\text{∈}[0,1] λip∈[0,1]及 λ p \lambda^p λp的非零元素数 ∥ λ d ∥ 0 = ⌈ α p m ⌉ \left\|\lambda^d\right\|_0\text{=}\left\lceil\alpha^pm\right\rceil λd 0=⌈αpm⌉
- 加权项:最大化 s p s^p sp与 λ p \lambda^p λp内积,使所有段落 Token \text{Token} Token的显著性合 ∑ i = 1 m u i p \displaystyle{}\sum_{i=1}^{m}u_{i}^{p} i=1∑muip最大,鼓励模型选择使得得分更高的 Token \text{Token} Token
- 熵项: λ p \lambda^p λp实际对于 s p s^p sp进行类 0/1 \text{0/1} 0/1二元选择,会导致结果离散不可微,故加入熵项以进行 ε \varepsilon ε平滑化以便梯度优化
- 训练迭代:初始化辅助变量 a p / b 1 p , b 2 p , . . . , n m p a^p/b_1^p,b_2^p,...,n_m^p ap/b1p,b2p,...,nmp为全 0 0 0
- 更新方式: a p ′ = ε ln k – ε ln { ∑ i exp ( s i p + b i p ε ) } \displaystyle{}{a}^{p\text{ }\prime}\text{=}\varepsilon\ln{k}\text{ – }\varepsilon\ln\left\{{\mathop{\sum}\limits_{i}\exp\left(\frac{{s}_{i}^p\text{+}{b}_{i}^p}{\varepsilon}\right)}\right\} ap ′=εlnk – εln{i∑exp(εsip+bip)}以及 b i ′ = min ( – s i – a ′ , 0 ) {b}_{i}^{\prime}\text{=}\min\left({–{s}_{i}–{a}^{\prime},0}\right) bi′=min(–si–a′,0)
- 最终输出:只需几轮迭代后,即可输出结果 λ i p = exp ( s i p + b i p + a p ε ) \lambda_i^p\text{=}\exp\left(\cfrac{s_i^p\text{+}b_i^p\text{+}a^p}{\varepsilon}\right) λip=exp(εsip+bip+ap)
3.1.3. \textbf{3.1.3. } 3.1.3. 如何确定稀疏性矩阵 A ~ \tilde{\textbf{A}} A~: 在小样本上的对齐适配
1️⃣一些稀疏对齐策略
- Top- k \text{Top-}k Top-k:对每个 q i q_i qi选取相关性评分最高的 k k k个文档向量,当 k =1 k\text{=1} k=1时退化为 ColBERT \text{ColBERT} ColBERT
- Top- p \text{Top-}p Top-p:对每个 q i q_i qi选取相关性评分最高的 max ( ⌊ p m ⌋ , 1 ) \max\left(\lfloor pm\rfloor,1\right) max(⌊pm⌋,1)个文档向量,其中 m m m为文档长度 p p p为对齐比例
2️⃣让稀疏对齐策略适应特定目标任务
- 训练阶段:在源域(通用检索语料库)上使用一个固定的对齐策略(如 Top-1 \text{Top-1} Top-1)训练 Aligner \text{Aligner} Aligner
- 适应阶段:在不改参数的前提下,基于目标任务完成以下步骤的调整
- 输入:目标域(目标任务语料库) { P ( 1 ) , P ( 2 ) , … , P ( N ) } \left\{P^{(1)},P^{(2)},\ldots,P^{(N)}\right\} {P(1),P(2),…,P(N)}及少量标注数据 { ( Q 1 , P + 1 ) , ( Q 2 , P + 2 ) , … , ( Q K , P + K ) } \left\{\left(Q^1, P_{+}^1\right),\left(Q^2,P_{+}^2\right), \ldots,\left(Q^K, P_{+}^K\right)\right\} {(Q1,P+1),(Q2,P+2),…,(QK,P+K)}
- 检索:用预训练模型为每个查询 Q i Q^i Qi检索得到候选段落 { P ( i 1 ) , P ( i 2 ) , … } \left\{P^{\left(i_1\right)}, P^{\left(i_2\right)}, \ldots\right\} {P(i1),P(i2),…}
- 评估:用不同的对齐策略( Top-0.1/Top-0.2/.../Top-1/Top-2/... \text{Top-0.1/Top-0.2/.../Top-1/Top-2/...} Top-0.1/Top-0.2/.../Top-1/Top-2/...)重新计算候选文档集中每个段落的得分并排序
- 适应:基于标注数据,选择评估阶段中排序效果(如 nDCG@10 \text{nDCG@10} nDCG@10)最佳的对齐策略,将其作为是用于该任务的对齐策略
3️⃣适配后的检索:以 Top-2 \text{Top-2} Top-2为例,用 A ~ \tilde{\textbf{A}} A~去选择 ( u q ⊗ u p ) (u^q\text{⊗}u^p) (uq⊗up)矩阵每行显著性积 ( u q ⊗ u p ) i j = u i q u j p (u^q\text{⊗}u^p)_{ij}\text{=}u^q_{i}u^p_{j} (uq⊗up)ij=uiqujp最大的两个元素

3.2. \textbf{3.2. } 3.2. 基于显著性的剪枝
1️⃣原始方法
- 嵌入:为 Q Q Q与 P = { P ( 1 ) , P ( 2 ) , … , P ( N ) } \mathscr{P}\text{=}\left\{P^{(1)},P^{(2)},\ldots,P^{(N)}\right\} P={P(1),P(2),…,P(N)}每个 Token \text{Token} Token都生成向量,即 Q = { q 1 , q 2 , … , q n } Q\text{=}\left\{q_{1},q_2,\ldots,q_{n}\right\} Q={q1,q2,…,qn}和 P ( j ) = { p 1 ( j ) , p 2 ( j ) , … , p m ( j ) } P^{(j)}\text{=}\{p_{1}^{(j)},p_{2}^{(j)},\ldots,p_{m}^{(j)}\} P(j)={p1(j),p2(j),…,pm(j)}
- 检索:让每个 q i ∈ Q q_i\text{∈}Q qi∈Q在所有段落子向量集 P ( 1 ) ∪ P ( 2 ) ∪ … ∪ P ( N ) P^{(1)}\text{∪}P^{(2)}\text{∪}\ldots\text{∪}P^{(N)} P(1)∪P(2)∪…∪P(N)中执行 MIPS \text{MIPS} MIPS(最大内积搜索),得到 Top- K \text{Top-}K Top-K的段落子向量
- 回溯:合并 n n n个 q i q_i qi的 MIPS \text{MIPS} MIPS结果得到 n × K n\text{×}K n×K个段落子向量,将每个子向量回溯到其所属段落得到 P ′ = { P ( 1 ) , P ( 2 ) , … , P ( M ) } \mathscr{P}^\prime\text{=}\left\{P^{(1)},P^{(2)},\ldots,P^{(M)}\right\} P′={P(1),P(2),…,P(M)}
- 重排:用基于 MaxSim \text{MaxSim} MaxSim的后期交互计算精确相似度评分 ( Q , P ) = ∑ i = 1 n max j = 1 … m q i ⊤ p j \displaystyle{}(Q,P)\text{=}\sum_{i=1}^{n} \max _{j=1 \ldots m} q_{i}^{\top} p_{j} (Q,P)=i=1∑nj=1…mmaxqi⊤pj,从而对 P ′ \mathscr{P}^\prime P′进行重排得到最相似段落
2️⃣剪枝方法
- 段落剪枝:用 u i p = λ i p ×ReLU ( W p p i + b p ) u_{i}^{p}\text{=}\lambda_{i}^{p}\text{×ReLU}\left(\textbf{W}^{p} {p}_{i}\text{+}b^{p}\right) uip=λip×ReLU(Wppi+bp)计算 P ( 1 ) ∪ … ∪ P ( N ) P^{(1)}\text{∪}\ldots\text{∪}P^{(N)} P(1)∪…∪P(N)中每个 Token \text{Token} Token的显著性,留下显著性排前 β p % β^p\% βp%的 Token \text{Token} Token
- 查询剪枝:用 u i q = λ i q ×ReLU ( W q q i + b q ) u_{i}^{q}\text{=}\lambda_{i}^{q}\text{×ReLU}\left(\textbf{W}^{q} {q}_{i}\text{+}b^{q}\right) uiq=λiq×ReLU(Wqqi+bq)计算 Q Q Q中每个 Token \text{Token} Token的显著性,同样只留下显著性排前 β q % β^q\% βq%的 Token \text{Token} Token
- 检索:让剩下的查询子向量 q i q_i qi集,对剩下的段落子向量 p j p_j pj集进行 MIPS \text{MIPS} MIPS搜索,后续回溯步骤不变
- 重排:将精确的距离评分从 MaxSim \text{MaxSim} MaxSim,变成基于稀疏矩阵的相似度评分 Sim ( Q , D ) = 1 Z ∑ i = 1 n ∑ j = 1 m ( S ∘ A ) i j \displaystyle\text{Sim}(Q,D)\text{=}\frac{1}{Z} \sum_{i=1}^{n} \sum_{j=1}^{m}(\textbf{S}\text{∘}\textbf{A})_{ij} Sim(Q,D)=Z1i=1∑nj=1∑m(S∘A)ij
4. \textbf{4. } 4. 实验概要
1️⃣实验的关键设置
- 模型配置:采用 Top-1 \text{Top-1} Top-1任务进行训练 Transformer \text{Transformer} Transformer,在 Ms-Marco \text{Ms-Marco} Ms-Marco上进行微调
- 检索过程:采用 ScaNN \text{ScaNN} ScaNN最邻近查询进行 MIPS \text{MIPS} MIPS,为每个 q i q_i qi查找 Top-4000 \text{Top-4000} Top-4000最邻近
- 对齐适配:采样 8 \text{8} 8个标记数据,在 k ∈ { 1 , 2 , 4 , 6 , 8 } k\text{∈}\{1,2,4,6,8\} k∈{1,2,4,6,8}和 p ∈ { 0.5 % , 1 % , 1.5 % , 2 % } p\text{∈}\{0.5\%,1\%,1.5\%,2\%\} p∈{0.5%,1%,1.5%,2%}上选择能最大化 nDCG@10 \text{nDCG@10} nDCG@10的策略
2️⃣实验的关键结果
- 检索性能: Aligner \text{Aligner} Aligner的性能优于单向量模型和 ColBERTv2 \text{ColBERTv2} ColBERTv2,并且仅需 8 \text{8} 8个标记样本就可使 Aligner \text{Aligner} Aligner完成对特定任务的适配
- 检索开销:高度剪枝后( β q = 50 % , β d = 40 % β^q\text{=}50\%,β^d\text{=}40\% βq=50%,βd=40%)性能仍接近未剪枝,更高程度的剪枝后性能仍然衰减不大,然而索引大大减小
- 可解释性:在具体的任务当中,模型能够自动识别关键的名词 / \text{/} /动词短语,并在不同任务中有不同的识别模式