【RL】KTO: Model Alignment as Prospect Theoretic Optimization

note

• 提出了一种新的对齐方法KTO，该方法通过直接最大化生成内容的效用，匹配或超过了基于偏好的对齐方法。研究表明，最佳的对齐损失函数取决于具体场景的归纳偏差，而非单一损失函数的普适性。KTO方法在数据收集和处理上具有显著优势，有望在实际应用中推广。

一、研究背景

研究问题：这篇文章要解决的问题是如何更好地对齐大型语言模型（LLMs）与人类反馈，以提高生成内容的有用性、事实性和伦理性。
研究难点：该问题的研究难点包括：人类反馈通常以偏好形式出现，而偏好数据稀缺且昂贵；现有的对齐方法在处理大规模模型时存在性能和稳定性问题。
相关工作：该问题的研究相关工作有：RLHF、DPO等基于偏好的对齐方法，以及条件SFT、序列似然校准等非基于偏好的对齐方法。

二、研究方法

这篇论文提出了一种新的对齐方法，称为Kahneman-Tversky优化（KTO），用于解决LLMs与人类反馈对齐的问题。具体来说，

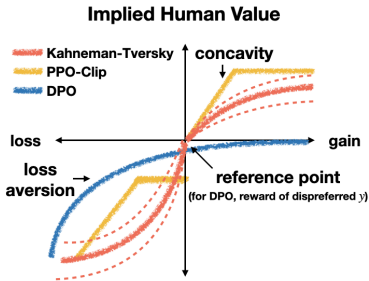
• 前景理论视角：首先，论文通过前景理论解释了现有对齐方法成功的原因，指出这些方法隐含地模型化了人类决策中的偏差，如损失厌恶。
• 人类感知损失函数（HALOs）：论文定义了一类新的损失函数，称为人类感知损失函数（HALOs），这些损失函数直接最大化生成内容的效用，而不是偏好对数似然。
• Kahneman-Tversky优化（KTO）：论文提出了KTO方法，该方法使用Kahneman和Tversky的前景理论模型来直接最大化生成内容的效用。KTO方法只需要一个二进制信号，即输出是否可取，这使得数据收集更便宜、更快。

• KTO（Kahneman-Tversky Optimization）方法的数学公式如下：

核心损失函数：

$$L_{\text{KTO}}({\pi }_{\theta },{\pi }_{ref})={\mathbb{E}}_{(x,y)\sim D}\left[{\lambda }_y-v(x,y)\right]$$

其中：

• $r_{\theta }(x,y)$：策略模型的相对对数概率比
  $$r_{\theta }(x,y)=\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)}$$

• $z_0$：策略模型与参考模型之间的KL散度
  $$z_0=\text{KL}({\pi }_{\theta }(y^{\prime }|x)\Vert {\pi }_{ref}(y^{\prime }|x))$$

• $v(x,y)$：基于Kahneman-Tversky前景理论的价值函数

三、实验设计

论文在多个模型家族上进行了实验，包括Pythia和Llama系列模型。实验设计包括以下几个方面：
数据集：实验使用了Anthropic-HH、OpenAssistant和SHP等多个数据集进行预训练和微调。
模型对比：实验对比了SFT、DPO、ORPO、KTO等方法在不同模型规模下的性能。
评估指标：使用GPT-4-0613对对齐模型的响应进行评价，评估指标包括有帮助性、无害性和简洁性。

四、结果与分析

• HALOs的性能：HALOs在每一个模型规模上都匹配或超过了非HALOs的性能，尤其是在13B以上的模型中，差异显著。

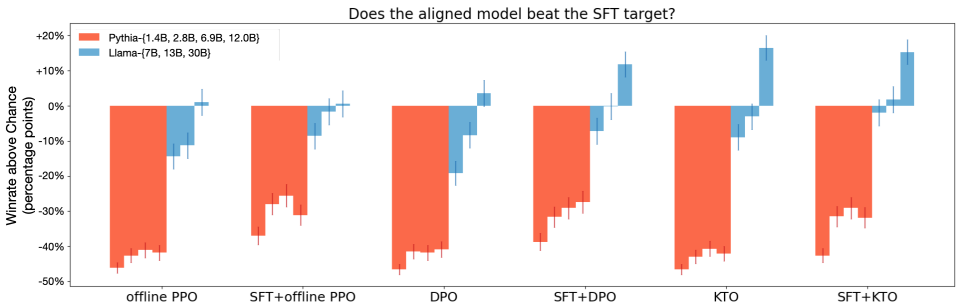
• KTO的优势：KTO在7B、13B和30B模型上均优于DPO，且在某些任务上表现尤为突出，如在GSM8K数据集上，KTO相较于DPO提升了13.5个百分点。
• 数据不平衡性：KTO能够处理极端的数据不平衡，使用高达90%的少期望示例仍能匹配DPO的性能。
• 无需SFT：在足够大的模型上，KTO可以直接跳过SFT阶段，而不会影响生成质量。

五、论文评价

1、优点与创新

提出了一种新的对齐方法：论文提出了Kahneman-Tversky Optimization (KTO)，该方法直接最大化生成物的效用，而不是像现有方法那样最大化偏好的对数似然。
数据效率更高：KTO只需要一个二进制信号（输出是否可取），这种数据在现实世界中更容易收集，成本更低，速度更快。
在多种规模上表现优异：KTO在1B到30B参数规模上匹配或超过了基于偏好的方法（如DPO）的性能。
处理极端数据不平衡的能力：KTO在使用高达90%更少可取示例的情况下，仍然能够匹配DPO的性能。
跳过监督微调的可能性：当预训练模型足够好时，可以直接使用KTO而无需监督微调，这在DPO中总是需要的。
理论解释：论文提供了理论解释，说明为什么KTO在某些情况下比DPO表现更好，特别是在处理噪声和不一致反馈时。

2、不足与反思

没有一种通用的HALO：论文指出，没有一种HALO是普遍优越的，最佳HALO取决于特定设置的最适合归纳偏差，这一选择应该是有意为之，而不是默认选择任何一种损失函数。
反馈数据的代表性问题：使用的反馈数据（如SHP、HH、OASST）可能不具代表性，可能会导致模型对齐到不具代表性的子集，从而阻碍其他人群同等受益。
未来工作方向：包括开发能够处理更细粒度反馈的HALO、适用于其他模态和模型类的HALO、能够根据不同的公平性定义解决反馈矛盾的HALO，以及设计用于在线数据的HALO。
生态有效评估：需要在实际环境中部署对齐模型，以评估不同HALO的优点，这是未来工作的一个重要方向。

六、相关问题

问题1：KTO方法如何在实验中表现出优于DPO的性能？

KTO方法在实验中表现出优于DPO的性能主要有以下几个原因：
数据效率：KTO方法只需要一个二进制信号（输出是否可取），这使得数据收集更便宜、更快。相比之下，DPO依赖于偏好数据，这些数据通常稀缺且昂贵。
处理极端数据不平衡的能力：KTO能够处理极端的数据不平衡，使用高达90%的少期望示例仍能匹配DPO的性能。而DPO在处理数据不平衡时可能会遇到困难。
无需SFT：在足够大的模型上，KTO可以直接跳过SFT阶段，而不会影响生成质量。而DPO通常需要SFT来达到最佳性能。
理论优势：KTO方法通过直接最大化生成内容的效用，而不是偏好对数似然，能够更好地反映人类的决策偏差，如损失厌恶。

问题2：KTO方法的理论基础是什么？

KTO方法的理论基础是Kahneman和Tversky的前景理论。前景理论解释了人类在不确定事件中的决策行为，指出人类决策中存在损失厌恶、风险厌恶等偏差。KTO方法通过以下方式利用前景理论：

价值函数：KTO使用Kahneman和Tversky的价值函数来衡量生成内容的效用。该函数在相对损失区域比相对增益区域更敏感，反映了人类的损失厌恶特性。
加权函数：虽然KTO主要关注价值函数，但加权函数也在一定程度上影响了模型的决策。KTO通过引入参考点来控制模型的决策行为。

KTO（Kahneman-Tversky Optimization）方法的数学公式如下：

核心损失函数：

$$L_{\text{KTO}}({\pi }_{\theta },{\pi }_{ref})={\mathbb{E}}_{(x,y)\sim D}\left[{\lambda }_y-v(x,y)\right]$$

其中：

• $r_{\theta }(x,y)$：策略模型的相对对数概率比
  $$r_{\theta }(x,y)=\log \frac{{\pi }_{\theta }(y|x)}{{\pi }_{ref}(y|x)}$$

• $z_0$：策略模型与参考模型之间的KL散度
  $$z_0=\text{KL}({\pi }_{\theta }(y^{\prime }|x)\Vert {\pi }_{ref}(y^{\prime }|x))$$

• $v(x,y)$：基于Kahneman-Tversky前景理论的价值函数

问题3：KTO方法在实际应用中有哪些潜在优势？

数据收集更容易：KTO方法只需要一个二进制信号（输出是否可取），这使得数据收集更便宜、更快，特别是在实际应用中，可以更容易地从用户反馈中收集数据。
适应性强：KTO方法不依赖于特定的数据分布，可以适应不同的应用场景和数据类型，具有更强的通用性。
稳定性高：KTO方法在处理极端数据不平衡时表现出色，且不需要复杂的奖励学习过程，因此在实际应用中可能更稳定。
理论支持：KTO方法基于前景理论，能够更好地反映人类的决策偏差，从而在实际应用中可能更有效地对齐模型与人类反馈。

Reference

[1] KTO: Model Alignment as Prospect Theoretic Optimization
[2] https://huggingface.co/docs/trl/main/en/kto_trainer