当前位置：首页 > news >正文

图神经网络分享系列-GraphSage(Inductive Representation Learning on Large Graphs) (二)

news 2025/11/17 11:14:04

一、提出的方法：GraphSAGE

嵌入生成算法（前向传播）

参数学习

1.1 嵌入生成（即前向传播）算法

算法1的直观理解

迭代步骤详解

聚合器架构灵活性

小批量扩展方法

与Weisfeiler-Lehman同构测试的关系

邻域定义

1.2 学习GraphSAGE的参数

1.3 聚合器架构

均值聚合器

LSTM聚合器

池化聚合器

上一篇文章：图神经网络分享系列-GraphSage(Inductive Representation Learning on Large Graphs) (二)

一、提出的方法：GraphSAGE

该方法的核心理念是学习如何聚合节点局部邻域的特征信息（例如相邻节点的度数或文本属性）。

嵌入生成算法（前向传播）

假设GraphSAGE模型参数已训练完成，算法首先生成节点的嵌入向量（见3.1节）。该过程通过采样和聚合邻域特征实现层次化表征学习。

参数学习

模型参数通过标准随机梯度下降（SGD）和反向传播技术进行优化（见3.2节）。训练目标是最小化基于图结构的损失函数，使嵌入保留节点间的拓扑关系。

1.1 嵌入生成（即前向传播）算法

本节描述嵌入生成或前向传播算法（算法1），该算法假设模型已完成训练且参数固定。具体而言，假设已学习到K个聚合函数的参数（记为AGGREGATEk，∀k ∈ {1, ..., K}），这些函数用于聚合来自邻居节点的信息；同时假设已学习到一组权重矩阵Wk（∀k ∈ {1, ..., K}），用于在模型的不同层或“搜索深度”之间传播信息。参数训练方法将在3.2节详述。

算法1的直观理解

该算法的核心在于每次迭代（或搜索深度）中，节点会聚合局部邻居的信息。随着迭代进行，节点逐步获取来自图中更远区域的信息。算法1描述了在输入完整图结构G=(V,E)及所有节点特征x_v (∀v∈V)情况下的嵌入生成过程，后续将说明如何推广到小批量(minibatch)场景。

迭代步骤详解

外层循环的每一步（对应搜索深度k）中， $h^k$ 表示节点当前深度的表示：
每个节点v∈V将其直接邻居集合{ $h^{k-1}_u$ , ∀u∈N(v)}的表示聚合为单一向量 $h^{k-1}_{N(v)}$ 。需注意，此聚合步骤依赖于外层循环前一次迭代（k-1）生成的表示，而k=0时的初始表示定义为输入节点特征。

聚合邻居特征向量后，GraphSAGE将节点当前表示 $h^{k-1}_v$ 与聚合的邻居向量 $h^{k-1}_{N(v)}$ 拼接，并将拼接后的向量输入带有非线性激活函数σ的全连接层，生成算法下一步的节点表示（即 $h^k_v$ , ∀v∈V）。最终深度K的输出表示记为z_v≡h^K_v。

聚合器架构灵活性

邻居表示的聚合可通过多种聚合器架构实现（算法1中的AGGREGATE占位符），具体架构选择将在后续章节讨论。

小批量扩展方法

在小批量场景下，给定输入节点集合后，需先向前采样所需邻域集合（至深度K），随后运行内层循环（算法1第3行）。此时不再遍历所有节点，而是仅计算满足当前深度递归所需的表示（完整小批量伪代码见附录）。

与Weisfeiler-Lehman同构测试的关系

GraphSAGE算法在概念上受到经典的图同构测试算法启发。若在算法1中满足以下条件：(i) 设K = |V|（节点总数）；(ii) 权重矩阵设置为单位矩阵；(iii) 使用合适的哈希函数作为聚合器（无非线性激活），则算法1即为Weisfeiler-Lehman（WL）同构测试的实例，也称为“朴素顶点细化”[32]。若算法1对两个子图输出的表示集合{zv , ∀v ∈ V}完全相同，WL测试会判定这两个子图同构。该测试在部分情况下可能失效，但对广泛的图类有效[32]。

GraphSAGE是WL测试的连续近似，它将哈希函数替换为可训练的神经网络聚合器。当然，GraphSAGE的目标是生成有用的节点表示而非测试图同构。然而，GraphSAGE与经典WL测试的关联为算法设计提供了理论背景，即通过学习节点邻域的拓扑结构来捕获图信息。

邻域定义

在本研究中，采用固定大小的邻居集合均匀采样，而非使用算法1中的完整邻域集，以确保每批计算量固定。具体而言，通过重载符号定义 ( N(v) ) 为从集合 ( ${u \in V : (u, v) \in E}$ ) 中均匀抽取的固定大小样本，并在算法1的每次迭代 ( k ) 中重新抽取不同样本。若不进行采样，单批次的内存和预期运行时间将不可预测，最坏情况下为 ( O(|V|) \。

相比之下，GraphSAGE的每批次空间和时间复杂度固定为 ( $O(\prod_{i=1}^{K} S_i)$ )，其中 ( $S_i$ )（ $( i \in {1, ..., K} )$ ）和 ( K ) 为用户指定常数。实践表明，当 ( K=2 ) 且 ( $S_1 \cdot S_2 \leq 500$ ) 时，该方法可取得高性能表现（详见第4.4节）。

1.2 学习GraphSAGE的参数

在完全无监督的环境中，为了学习有用且具有预测性的表示，对输出表示 $z_u, \forall u \in V$ 应用基于图的损失函数，并通过随机梯度下降调整权重矩阵 $W^k, \forall k \in {1, ..., K}$ 以及聚合函数的参数。该损失函数促使相邻节点的表示尽可能相似，同时确保差异较大的节点表示显著不同。

v 是与节点 u 在固定长度随机游走中共同出现的邻近节点，σ 是 sigmoid 函数，Pn 是负采样分布，Q 定义了负样本的数量。值得注意的是，与之前的嵌入方法不同，输入此损失函数的表示 zu 是由节点局部邻域内的特征生成的，而非通过嵌入查找为每个节点训练唯一的嵌入。

这一无监督设置模拟了节点特征作为服务或静态存储库提供给下游机器学习应用的场景。如果生成的表示仅用于特定下游任务，无监督损失（公式 1）可以直接替换或通过任务特定目标（例如交叉熵损失）进行增强。

1.3 聚合器架构

与在N维网格（如句子、图像或3D体积）上进行的机器学习不同，节点的邻居没有自然顺序；因此，算法1中的聚合器函数必须对无序向量集合进行操作。理想的聚合器函数应具备对称性（即对输入排列保持不变），同时可训练且保持高表示能力。这种对称性确保了神经网络模型能在任意顺序的节点邻域特征集上训练和应用。

研究了三种候选聚合器函数：

均值聚合器

第一种候选函数是均值算子，即对集合 {h<sup>k−1</sup>, ∀u ∈ N(v)} 中的向量逐元素取平均。该聚合器几乎等同于转导式GCN框架[17]中的卷积传播规则。具体而言，通过将算法1中的第4、5行替换为以下内容，可推导出GCN方法的归纳式变体：

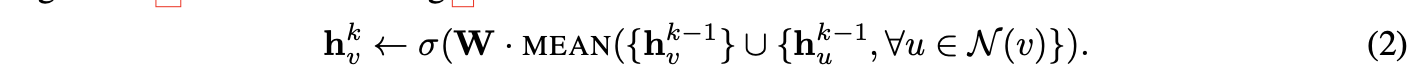
该聚合器是对局部谱卷积[17]的粗略线性近似。这种卷积聚合器与其他提出的聚合器的关键区别在于：它不执行算法1第5行中的拼接操作——即卷积聚合器不会将节点前一层的表示 $h^{k-1}$ 与聚合后的邻居向量 $h^{k}_{\mathcal{N}(v)}$ 拼接。

LSTM聚合器

另一种基于LSTM架构的复杂聚合器也被研究。相比均值聚合器，LSTM具有更强的表达能力。但需注意，LSTM本身不具备对称性（即非排列不变），因其按顺序处理输入。为适配无序的邻居集合，LSTM被随机应用于节点的邻居排列。

池化聚合器

最后一种聚合器兼具对称性和可训练性。在该池化方法中，每个邻居向量独立输入全连接神经网络，经变换后通过逐元素最大池化操作聚合邻居集信息：

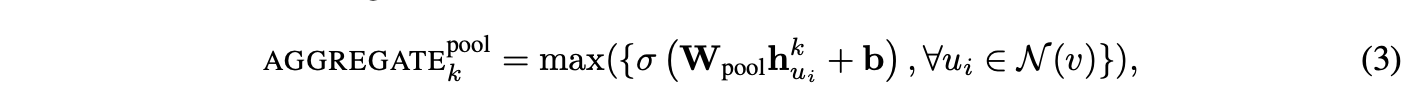
max表示逐元素的最大值运算符，σ是非线性激活函数。理论上，在最大池化之前应用的函数可以是一个任意深度的多层感知机，但本研究中聚焦于简单的单层架构。这种方法的灵感来源于近期在将神经网络架构应用于通用点集学习方面的进展[29]。直观来看，多层感知机可视为一组函数，用于为邻域集中的每个节点表征计算特征。通过对每个计算出的特征应用最大池化运算符，模型能有效捕捉邻域集的不同特性。还需注意的是，理论上任何对称的向量函数均可替代max运算符（例如逐元素的均值）。在开发测试中，最大池化与均值池化未表现出显著差异，因此后续实验均采用最大池化。

本篇内容讲解就到这里，下一篇会详细介绍实验～

传送门：

查看全文

http://www.dtcms.com/a/619093.html