洛谷 P3935 Calculating——因数个数定理+整除分块(数论分块)
P3935 Calculating
首先有一个东西叫因数个数定理。
就是题目中的x=p1k1p2k2⋯pnknx=p_1^{k_1}p_2^{k_2}\cdots p_n^{k_n}x=p1k1p2k2⋯pnkn,那么xxx的因数的个数为(k1+1)(k2+1)⋯(kn+1)(k_1+1)(k_2+1)\cdots (k_n+1)(k1+1)(k2+1)⋯(kn+1)。
证明
根据短除法可知,任何一个不小于222的数,都可以分解成若干个素数相乘;
又因为,ab=axab−xa^b=a^xa^{b-x}ab=axab−x(其中0≤x≤b0\leq x \leq b0≤x≤b);
所以nnn个相同的数可以被分成b−0+1=b+1b-0+1=b+1b−0+1=b+1个不同的数乘以某个数;
即对于∀i\forall i∀i,pikip_i^{k_i}piki含ki+1k_i+1ki+1个不同的整数(且他们的质因数只有pip_ipi);
最后根据乘法原理,就得出上式。
显而易见,这道题就变成了,求lll到rrr中所有数字的因数个数和。
因为数很多,所以枚举每个数字并计算它的因素的个数。显然是要TLE的。
考虑到,肯定会有很多数存在公因数,因此我们枚举每个因数显然更快一些。
现在再引入类似前缀和的原理,我们先求[1,l)[1,l)[1,l)中所有数字的因数个数和,再求[1,r][1,r][1,r]中所有数字的因数个数和,最后相减就是答案([l,r][l,r][l,r]中所有数字的因数个数和)了。
t1=∑i∈[1,l)g(i)t2=∑i∈[1,r]g(i)ans=∑i∈[l,r]g(i)=t2−t1t_1=\sum_{i\in[1,l)}g(i)\\ t_2=\sum_{i\in[1,r]}g(i)\\ ans=\sum_{i\in[l,r]}g(i)=t_2-t_1 t1=i∈[1,l)∑g(i)t2=i∈[1,r]∑g(i)ans=i∈[l,r]∑g(i)=t2−t1
- 其中g(i)g(i)g(i)表示iii的因数个数
上文的∑i∈[1,x]g(i)\sum_{i\in[1,x]}g(i)∑i∈[1,x]g(i)到底怎么快速求解呢?
我们先将式子转化一下:
∑i∈[1,x]g(i)=∑i=1n∑j∣i1=∑i=1n⌊ij⌋\sum_{i\in[1,x]}g(i)=\sum_{i=1}^{n}\sum_{j|i}1=\sum_{i=1}^{n}{\lfloor \frac {i}{j}\rfloor} i∈[1,x]∑g(i)=i=1∑nj∣i∑1=i=1∑n⌊ji⌋
- 其中x∣yx|yx∣y表示xxx整除yyy(yyy整除以xxx(ymodx=0y\mod x=0ymodx=0))
解释
求[1,n][1,n][1,n]中所有因数的个数(∑i∈[1,x]g(i)\sum_{i\in[1,x]}g(i)∑i∈[1,x]g(i));最直接的办法就是先枚举[1,n][1,n][1,n](∑i=1n\sum_{i=1}^{n}∑i=1n),再枚举其中每个数的因数,并累加数量∑j∣i1\sum_{j|i}1∑j∣i1;跟前面说的一样,枚举每个因数显然会快一些,因此我们就可以枚举[1,n][1,n][1,n],并求出该数字在nnn以内的整倍数数量(∑i=1n⌊ij⌋\sum_{i=1}^{n}{\lfloor \frac {i}{j}\rfloor}∑i=1n⌊ji⌋)。
显然,这样做可以把时间复杂度从O(n2)O(n^2)O(n2)降到O(n)O(n)O(n),但还不够。
注意到,总会有相邻的几个数在范围内的整倍数相同,那我们就尝试把整倍数书相同的(当然就相邻的)几个数分为一块儿,一起求解;这就是整除分块。
为了方便理解,我们观察图像(n=10n=10n=10)。
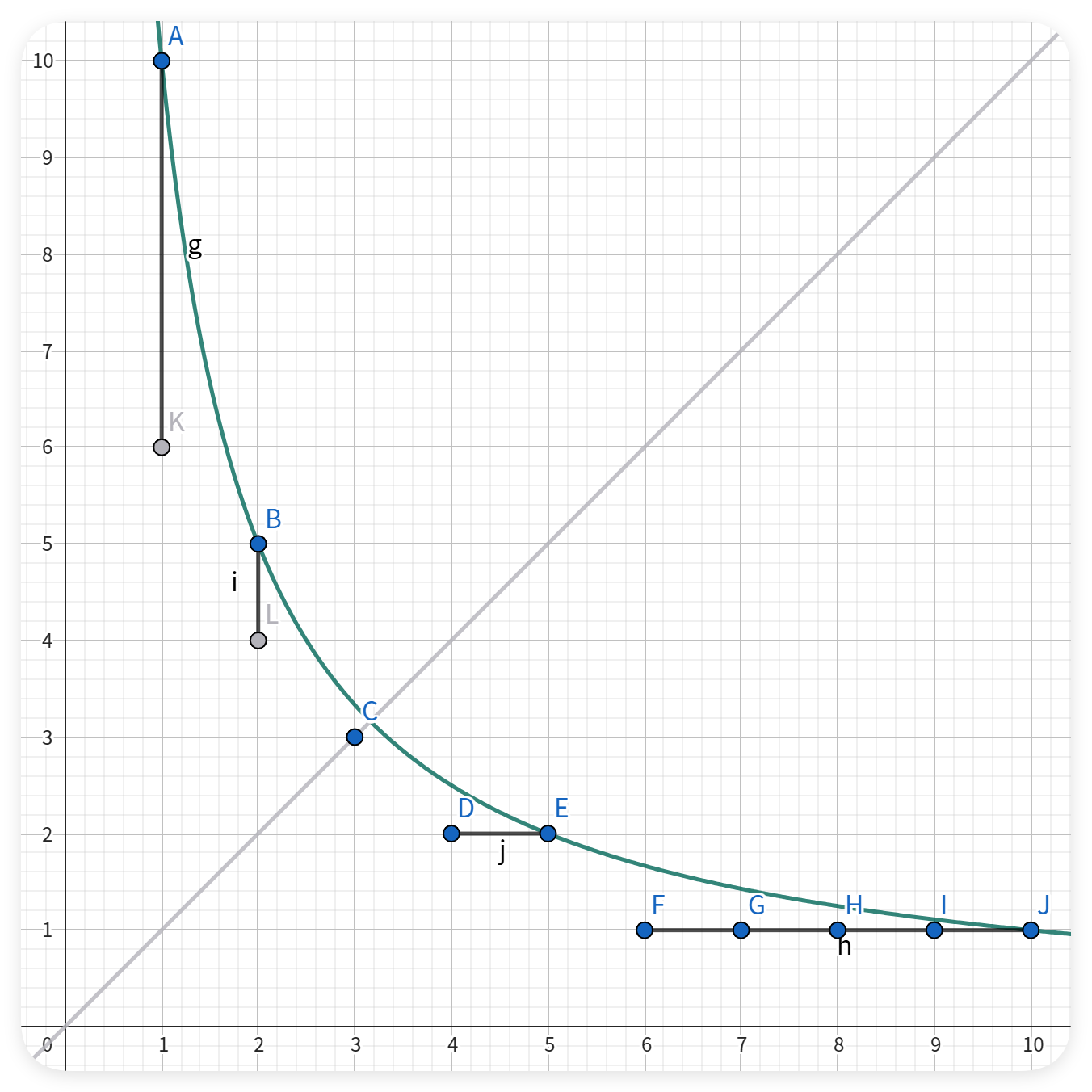
- (横着的)xxx轴:遍历[1,n][1,n][1,n]的每个数
- (竖着的)yyy轴:对应的数的整倍数数
显然,这是一个反比例函数(解析式为y=nxy=\frac{n}{x}y=xn),它关于y=xy=xy=x对称,交对称轴于(n,n)(\sqrt n, \sqrt n)(n,n)。
因此,我们可以把nnn分成两个部分(区间),分别是i<=ni<=\sqrt ni<=n和i>ni>\sqrt ni>n(xxx相当于iii):
-
对于i<=ni<=\sqrt ni<=n的部分,其kf≤−1k_f\leq-1kf≤−1(仅i=ni=\sqrt ni=n时kf=−1k_f=-1kf=−1)(kfk_fkf表示斜率),每个点对应的答案各不相同;
-
对于i>ni>\sqrt ni>n的部分,其kf>−1k_f>-1kf>−1;会出现有些点对应的答案相同的情况。
第一种情况暴力枚举[1,n][1,\sqrt n][1,n]就好了(时间复杂度O(n)O(\sqrt n)O(n))。
而第二种情况我们怎么知道哪些点对应的答案相同呢?
——根据函数的对称性。(还是上图)
描的每个蓝点代表对应的iii对应的答案。
我们任取一点DDD,求它所在的相同答案区间的右界。
因为函数的对称性,所以我们可以直接把DDD点对应(映射)到LLL点,而DDD点所在的区间的右界就是LLL所在区间(严格来说只能是一条线段)的上界(BBB点)。
这是怎么求出来的呢?直接说结论:(x,y)(x,y)(x,y)关于y=xy=xy=x的对称点为(y,x)(y,x)(y,x)。
证明
因为y=xy=xy=x是平面直角坐标系第一象限和第三象限的角平分线;
所以xxx轴与yyy轴互为关于y=xy=xy=x对称关系;
所以找(x,y)(x,y)(x,y)关于y=xy=xy=x的对称点相当于互换了坐标轴,得到(y,x)(y,x)(y,x)。
因此,i>ni>\sqrt ni>n时我们可以先求出iii对应的答案yyy,然后再求出yyy对应的答案,就是iii所在区间的右界了。
每个区间的总答案就是其中任意一个点的答案乘以区间长度。
这样的操作只会进行n\sqrt nn次(n\sqrt nn左边有nnn个点,n\sqrt nn右边就有nnn个区间),因此时间复杂度也是O(n)O(\sqrt n)O(n)。
#include<cstdio>
#include<cmath>
inline long long read(){ //快读char t;long long x=0;do{t=getchar();}while(t<'0' || '9'<t);while('0'<=t && t<='9'){x=x*10+t-'0';t=getchar();}return x;
}
constexpr long long mod=998244353;
inline long long sum(long long x){long long s=0;for(long long i=1; i<=sqrt(x); ++i) s+=x/i; //sqrt(x)以内直接枚举for(long long i=sqrt(x)+1, t; i<=x; i=t+1){t=x/(x/i); //当前区间的右界s+=x/i*(t-i+1); //当前区间的总答案((t-i+1)就是区间长度)s%=mod;}return s;
}
int main(){long long l, r;l=read();r=read();printf("%lld", (sum(r)-sum(l-1)+mod)%mod); //经过取模,不能保证sum(r)>sum(l-1)return 0;
}
