计算机图形学·14 经典视图（Classical Viewing）

本文是记录专业课计算机图形学的部分笔记，参考教材为Angel的第八版交互式计算机图形学——基于WebGL 2.0的自顶向下方法。

1、为什么需要经典视图（Classical Viewing）？存在许多传统由手工操作的制图工作（某些电影中的动画、大量建筑图或机器零件图纸），这些领域中需要不同的经典视图（如等角投影/等轴测图isometrics，正视图elevation，透视图Perspective）。而经典视图与计算机视图之间的对比关系，表明了在大多数API中所采用方法的长处（经典照相机vs合成照相机）。
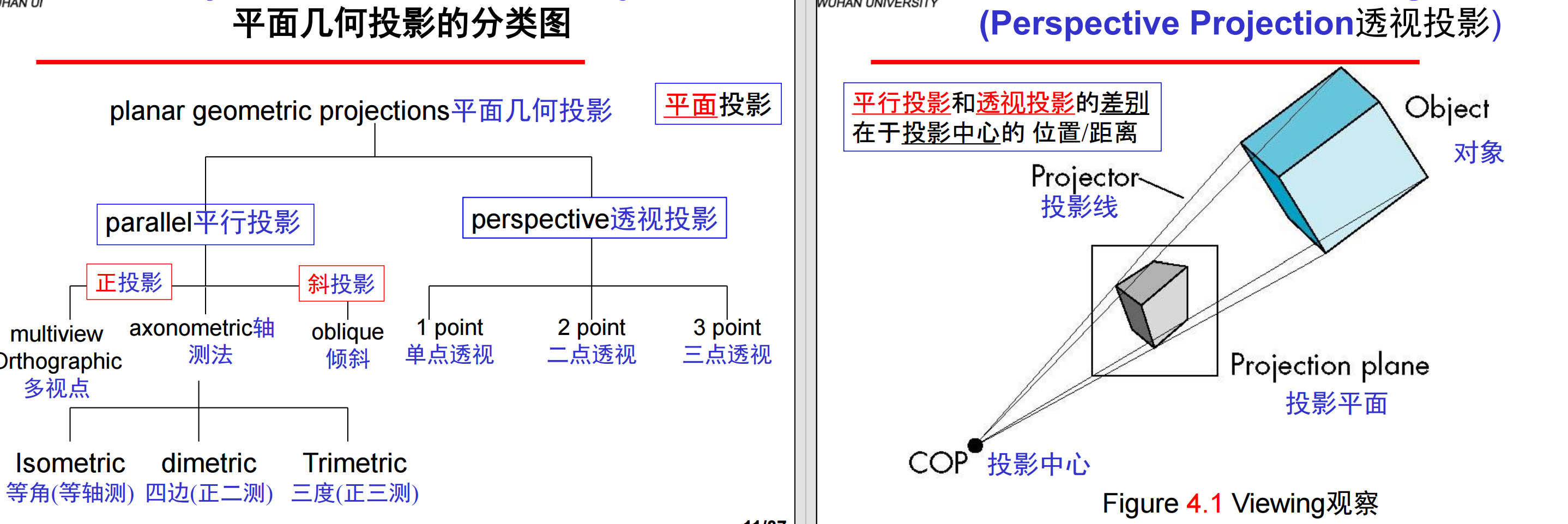
2、视图中需要三个基本要素：一个或多个对象、带有一个投影面的观察者、从对象到投影平面的投影线，经典视图就是基于这些要素之间的关系的（每个对象都假定是用平面的基准面构造出来的）。Planar Geometric Projections平面几何投影即投影到平面上的标准投影，投影线为直线，这些直线汇聚于投影中心或彼此平行，这种投影保持共线性但不一定保角。在诸如地图绘制等应用中也需要非平面投影。

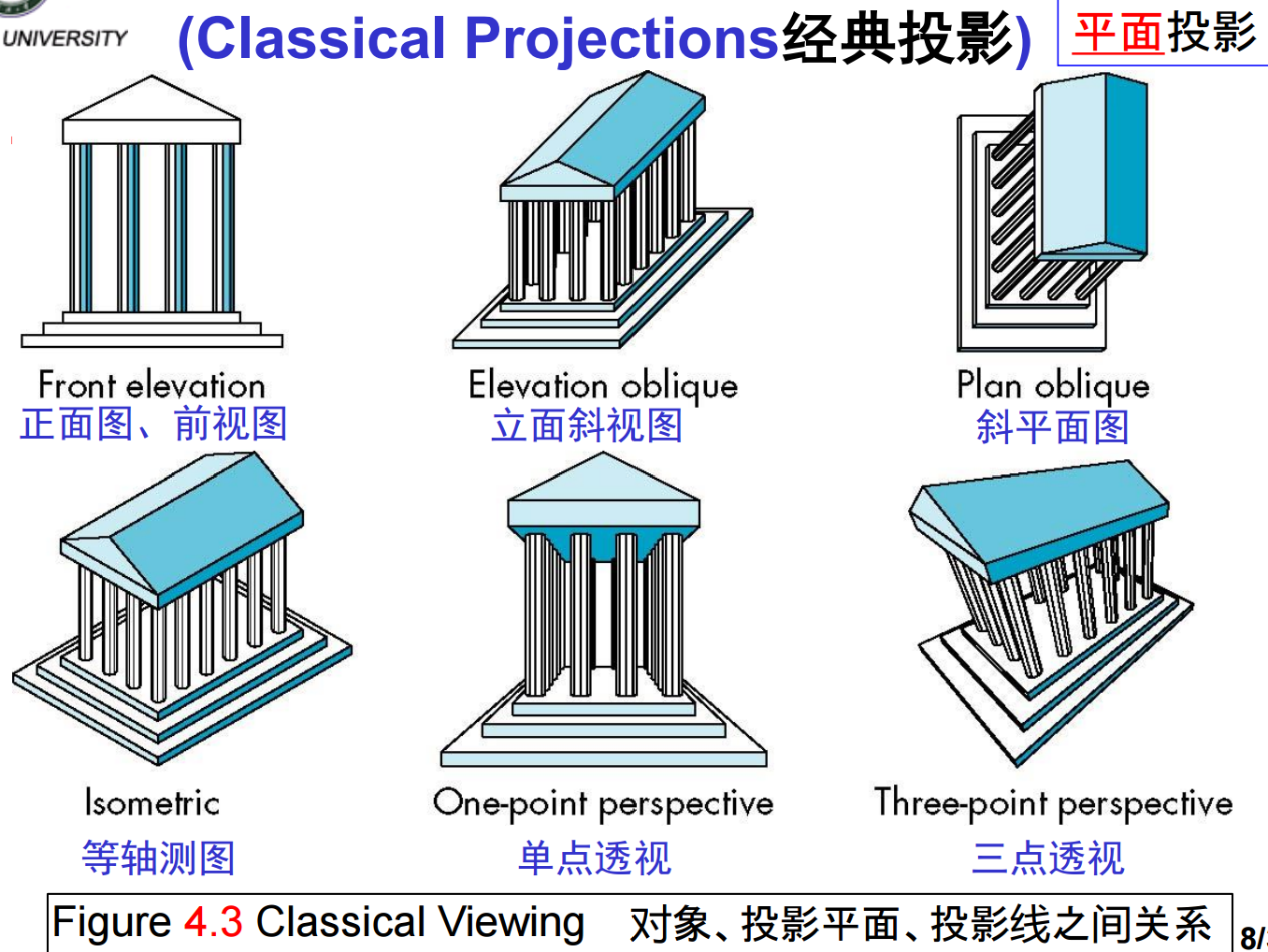
3、在诸如建筑业等实际应用中，所观察的对象通常由许多平坦面构成。这些面中任一个都可以认为是一个基准面(Principal faces) ，从而进行定位。特别地，根据习惯，对于比较规则物体，例如房屋，按照通常的方式可以定义前、后、左、右、顶、底等面。许多对象上都有几个面相交于直角，从而可以得到三个正交的方向（称为基准方向）和基准面。这其实是假设、想象出来、符合大众先验的建模坐标系统（对象坐标系统）。
4、计算机图形学中把所有的投影用同样的方法处理，用一个流水线体系实现它们。在经典视图中为了绘制不同类型的投影，发展出来不同的技术，其基本区别在于平行投影和透视投影（虽然从数学上说，平行投影是透视投影的极限状态）。


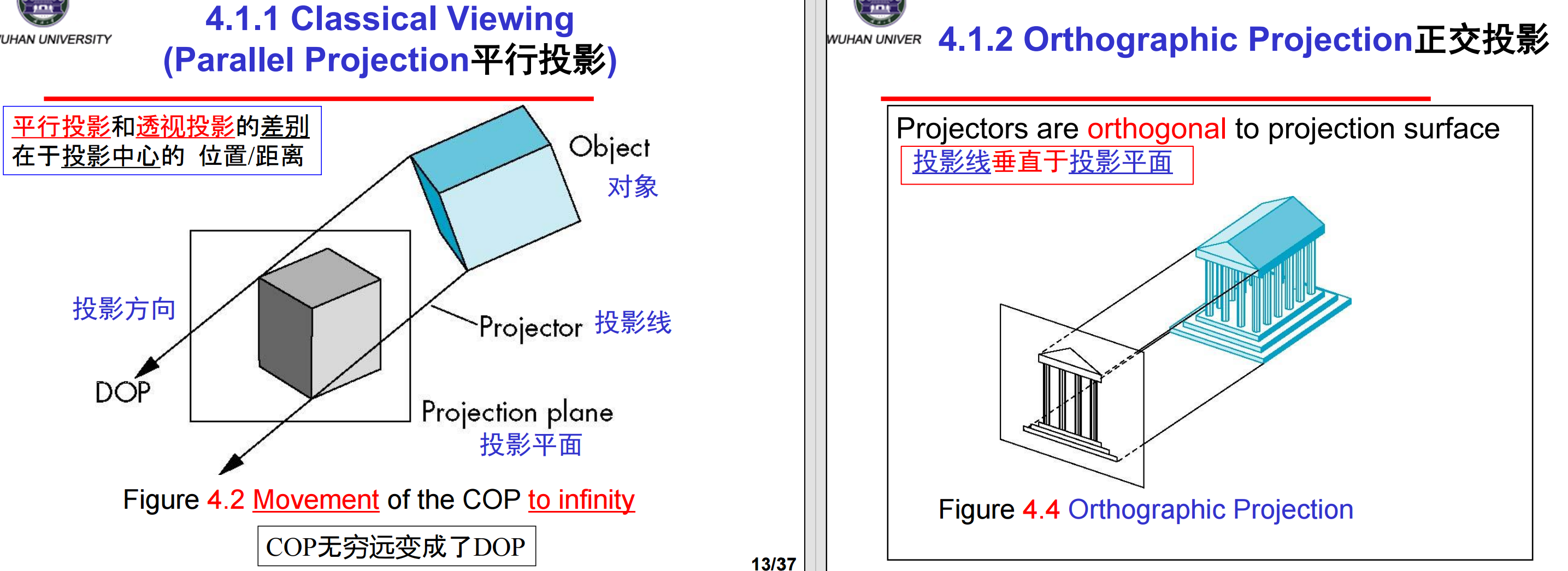
5、多视点正投影（Multiview Orthographic Projection）的优点是保持了距离与角度，可以保持形状、用来测量或建筑规划，缺点是不能看到对象真正的全局形状，因为许多面在视点中不可见（因此有时加上等角图）。

6、而在另一类正投影中，投影面不再平行基准面，这是轴测投影（Axonometric Projections）。投影面相对于对象基准面有一定的夹角，可以根据对立方体进行投影时一个角点处有多少个角相等（对称性）进行分类：①none没有——trimetric三度(正三测)；②two两个——dimetric四边(正二测)；③three三个——isometric等角(等轴测)。相当于把局部坐标（对象box）以某种角度投影到投影平面（观察坐标）上。

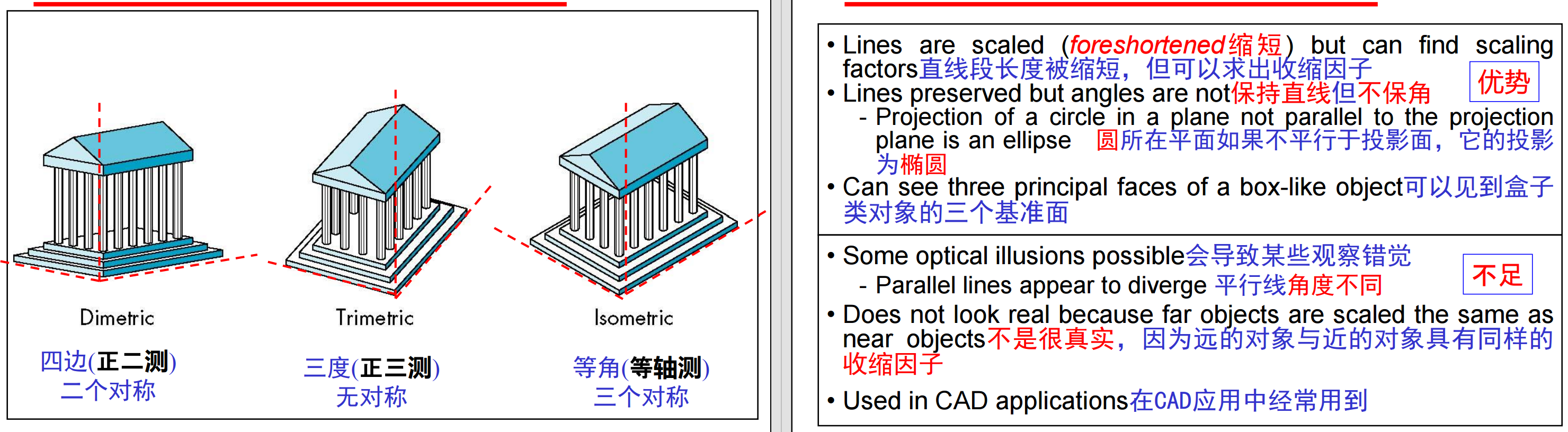
7、而在倾斜投影（Oblique Projections）中，投影线与投影面之间可以是任意角度：

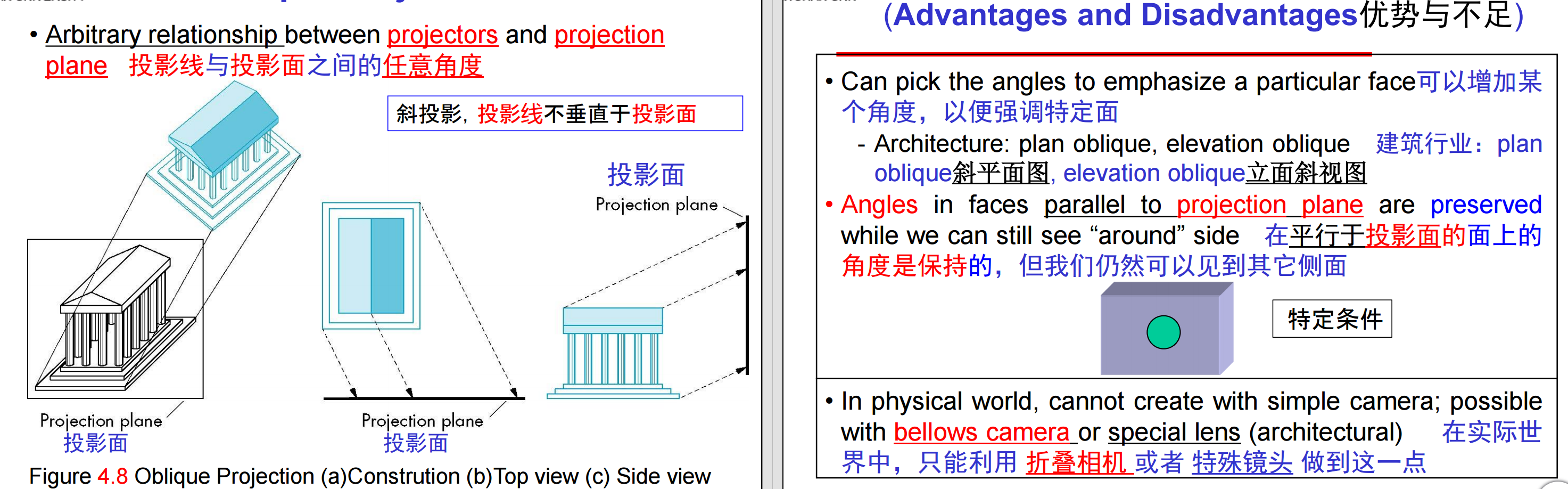
8、在透视投影（Perspective Projection）中，投影线汇聚于投影中心（COP）。其中，不平行于投影平面的一组平行线，经过透视投影之后收敛于一点，称为灭点（vanishing point），常用于代表景深。而主灭点是对象上平行于基准面坐标系（对象的建模坐标系）坐标轴方向的一组平行线（最多三组）的灭点，主灭点的个数决定一点透视/两点透视/三点透视。可以改变投影面的方位以控制主灭点的数目。
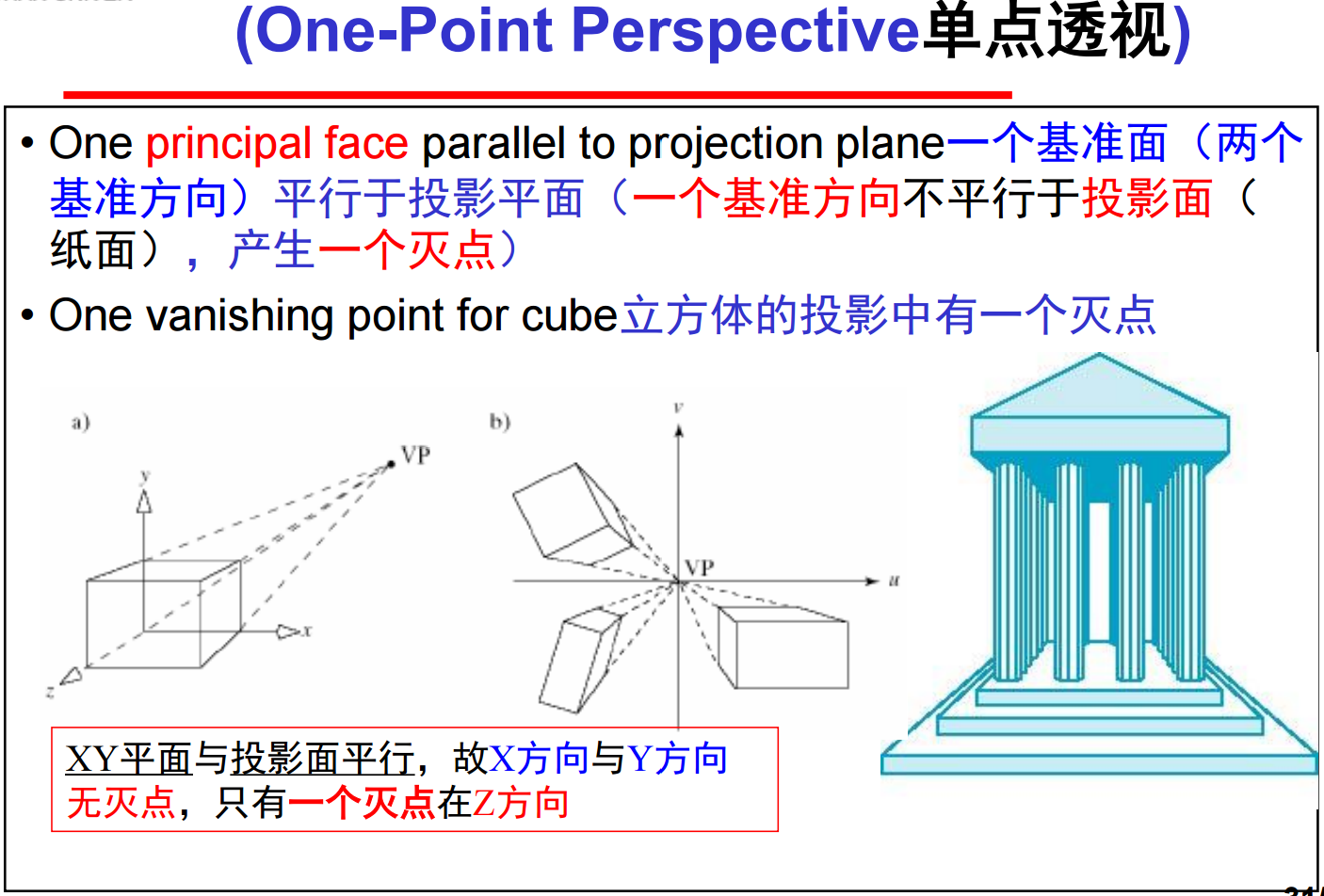
① 一点透视：
投影平面与对象局部坐标系的一个平面平行（这样，平行于坐标轴，并且不平行于投影平面的平行线只有一个方向）。

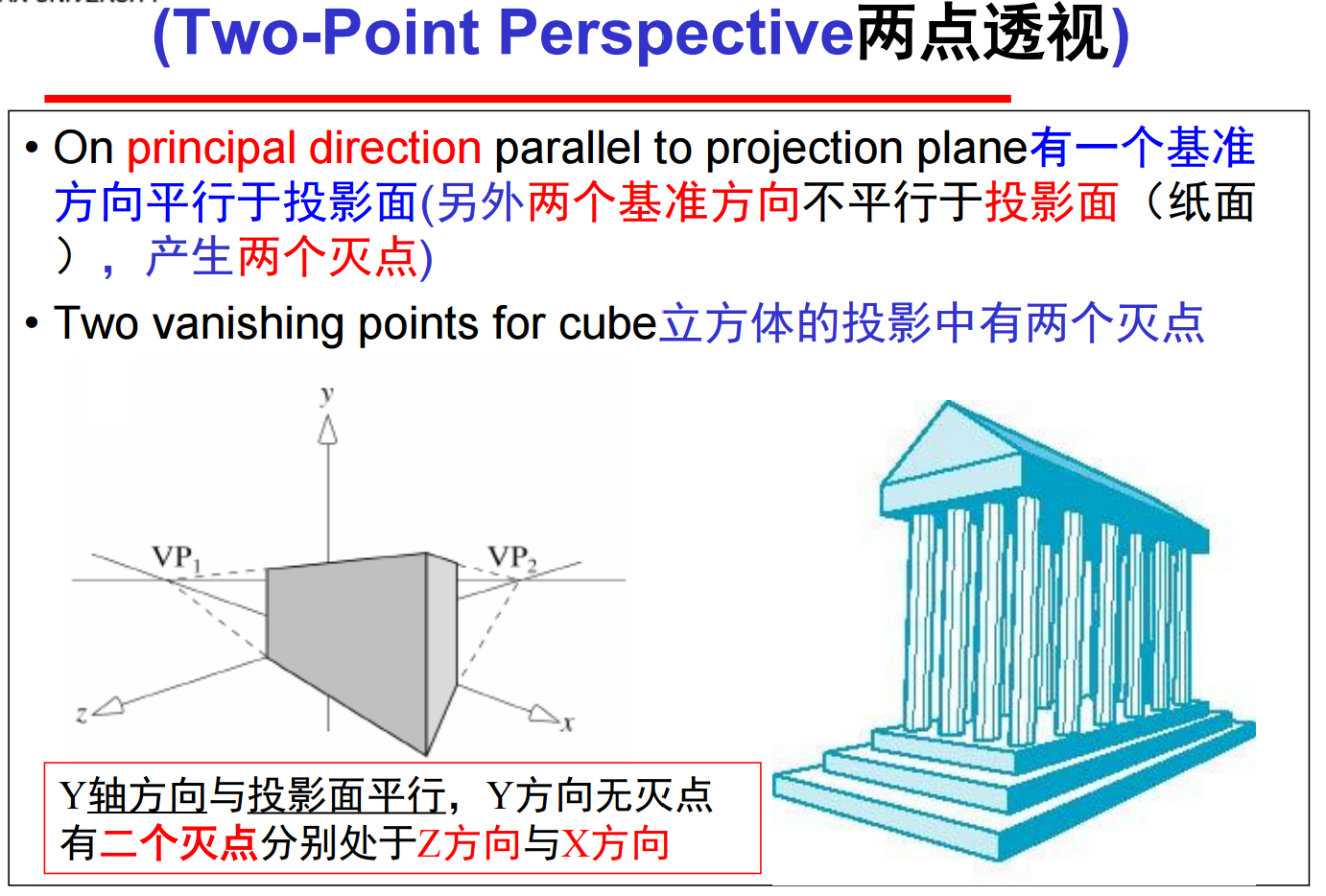
② 二点透视：
投影平面与对象局部坐标系的一根坐标轴平行而与另两根坐标轴成一定角度（平行于坐标轴并且不平行于投影平面的平行线则有二个方向）。

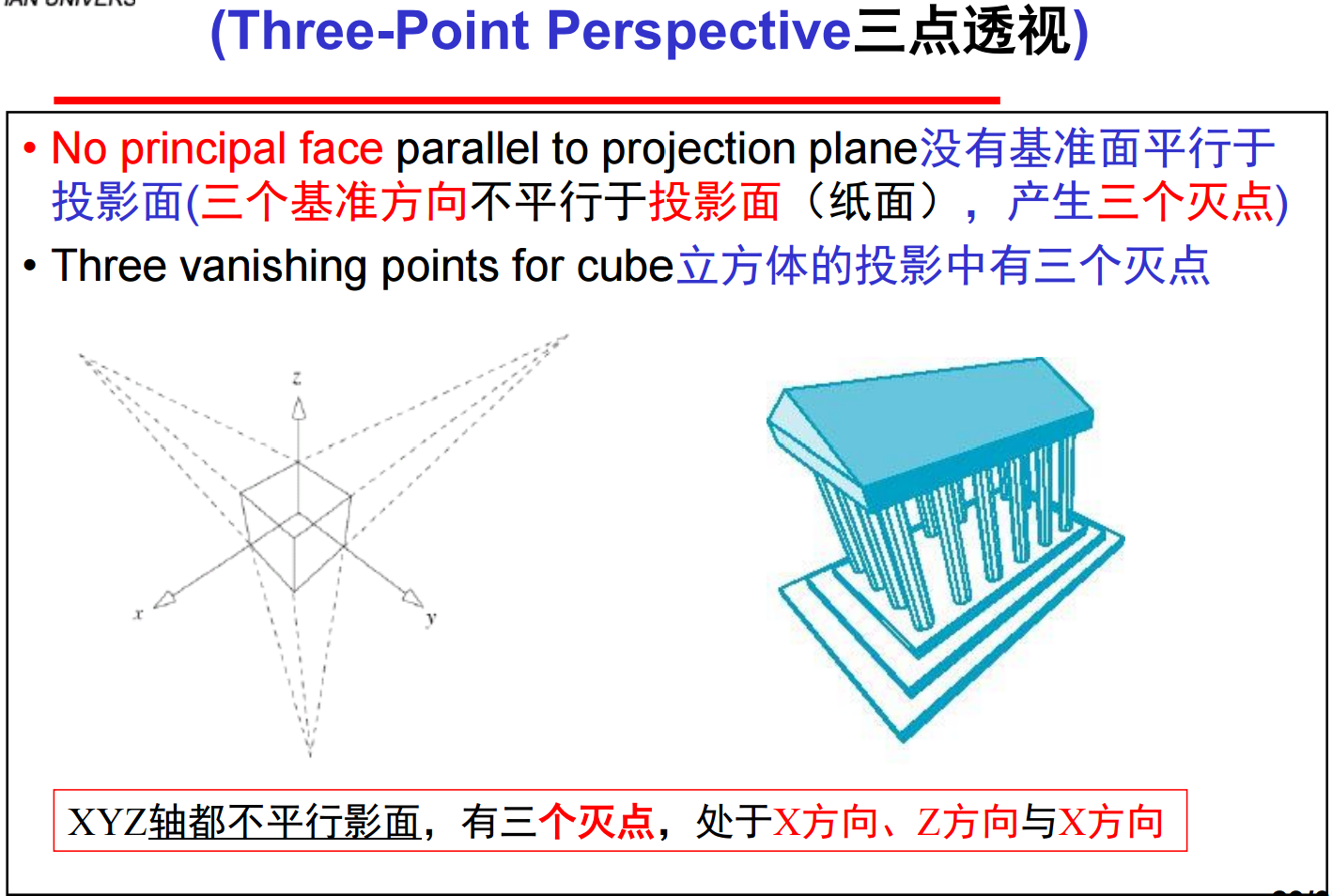
③ 三点透视：
投影平面与对象局部坐标系的三根坐标轴均有一定的角度（平行于坐标轴并且不平行于投影平面的平行线就有三个方向）。三点透视用得不多，主要原因是它难于构造。

透视投影的优势是同样大小的对象，离视点越远，投影结果就越小（diminuition），这样看起来更真实。但是，沿一条直线等距的几点投影后不一定等距（非均匀收缩），只有在平行于投影面的平面上角度被保持，相对于平行投影而言，更难用手工进行绘制（但对计算机而言，没有增加更多的困难）。
9、对于投影的性质，射影几何中对此进行了详尽的研究Rn+1中所有一维线性子空间看作n维射影空间的元素，记作Pn。给定Rn+1空间到自身的一个正则线性变换，那么它诱导出Pn上的变换称为射影变换（投影变换）。所有的射影变换都可以分解为有限个透视的复合。