昆明网站制作报价安卓手机网页视频怎么下载
专题一 联合分布函数
1.二维随机变量的定义
设,
为样本空间
上的两个随机变量,称
为二维随机变量。
实值函数,样本点的函数
2.联合分布函数的定义
设为二维随机变量,对任意实数
,称
为
的联合分布函数,简称分布函数。
3.联合分布函数的性质
1.非负规范性
,
,
;
2.单调不减性
关于
和
均单调不减;
3.右连续性
关于
和
均右连续;
。
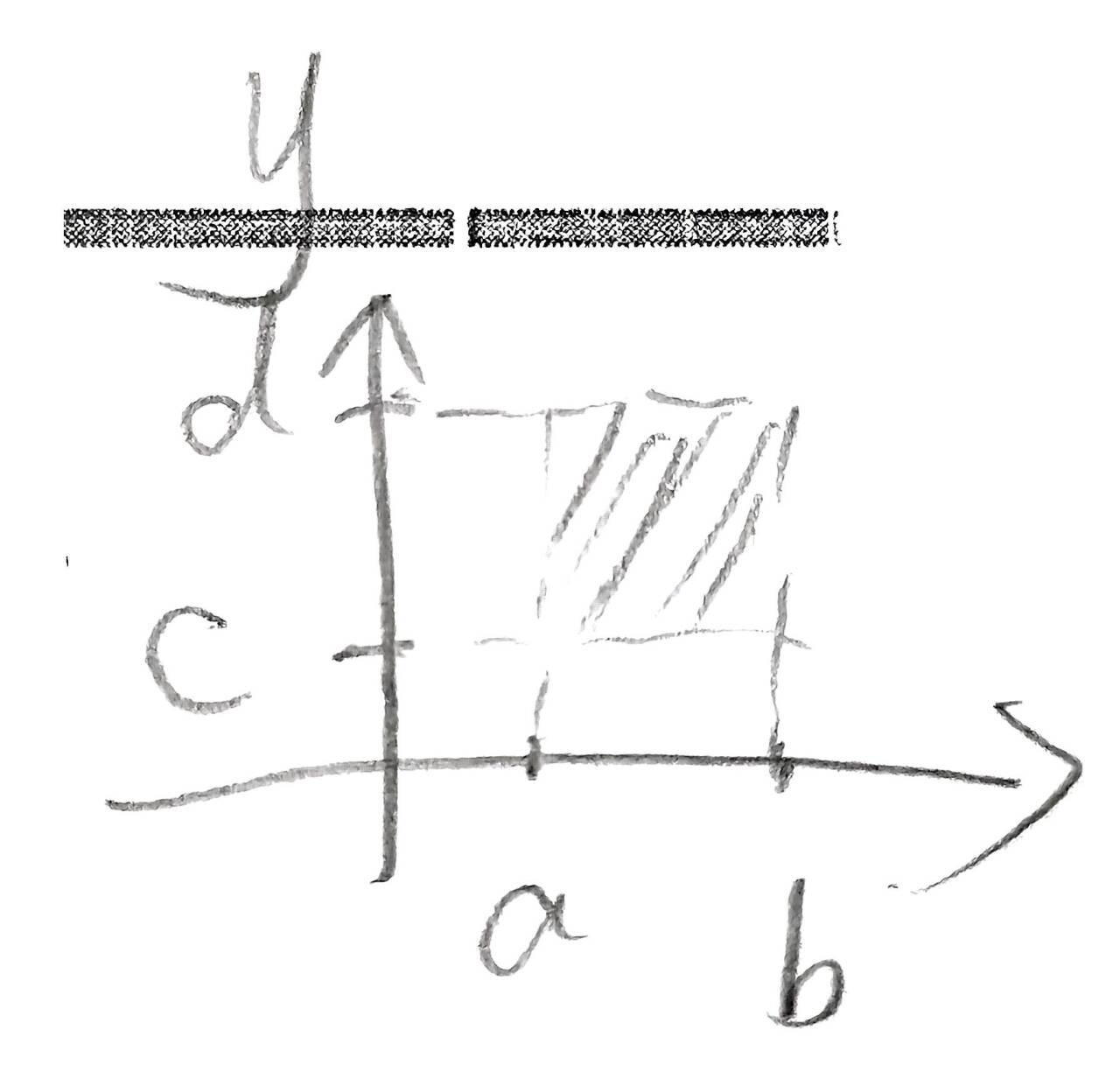
评注:性质(1)、(2)、(3)、(4)构成联合分布函数的充要条件。
4.边缘分布函数的定义
设二维随机变量的联合分布函数为
,分别称
为关于
和
的边缘分布函数。
求自己方向的概率
专题二 二维离散型随机变量
1.联合概率分布的定义
设二维随机变量的取值为有限个或可列个,称
为二维离散型随机变量。
设的取值为
,
称为
的联合概率分布,简称概率分布,也可用列表法表示。
2.联合概率分布的性质
【评注】性质(1)、(2)构成联合概率分布的充要条件。
3.边缘概率分布的定义
设二维随机变量的联合概率分布为
,分别称
第i行概率的和
第j列概率的和
为关于
和
的边缘概率分布。
4.条件概率分布的定义
设二维随机变量的联合概率分布为
,
称为在
的条件下,
的条件概率分布;
称为在
的条件下,
的条件概率分布。
专题三 二维连续型随机变量
1.联合概率密度的定义
设二维随机变量的联合分布函数为
,若存在非负可积函数
,对任意实数
,有
,则称
为二维连续型随机变量,
为
的联合概率密度,简称概率密度。二重反常变限积分
2.联合概率密度的性质
1.非负性:,
,
2.归一性:
3.★概率计算:
求X,Y取值的概率,将X,Y改为x,y,对联合概率密度的二重积分
4.导数关系:在的连续点处有
评注:性质(1)和(2)构成联合概率密度的充要条件。
3.边缘概率密度的定义
设二维随机变量的联合概率密度为
,分别称
为关于
和
的边缘概率密度。
4.条件概率密度的定义
设二维随机变量的联合概率密度为
,称
为在的条件下,
的条件概率密度;
称
为在的条件下,
的条件概率密度。
专题四 随机变量的独立性
1.随机变量相互独立的定义
设二维随机变量的联合分布函数为
,边缘分布函数分别为
和
。
若对任意实数,有
则称与
相互独立。(互不影响
2.随机变量相互独立的充要条件
与
相互独立
2.离散型:
3.连续型:
评注:若与
独立,
为连续函数,则
与
独立。
专题五 二维均匀分布与二维正态分布
1.二维均匀分布
设的联合概率密度为
其他
称服从区域
上的均匀分布,记作
。
性质:
若,则
,
,且
与
独立。
2.二维正态分布
的联合概率密度为
其中,
,记作
。
性质:
二维正态分布两个边缘分布均为一维正态分布,反之不成立,独立时成立
特别地:若与
独立,则
。
- 边缘分布:
(反之不成立)。
- 独立性与相关性:
与
独立
(X与Y不相关)。
- 线性组合:
。
相互独立的正态分布的线性组合仍为正态分布
专题六 二维随机变量函数的分布
1.二维离散型随机变量函数的分布
【例 3.8】设二维随机变量的联合概率分布为
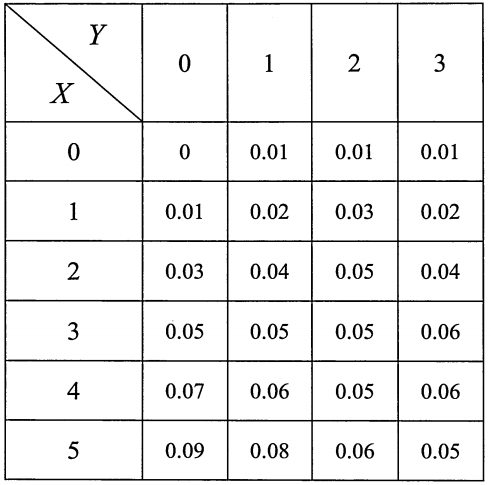
求:
(1),
;
(2)的概率分布;
(3)的概率分布;
(4)的概率分布。
【详解】
(1)
(2)
例如求V=2的概率分布,那么X取2,Y取2,1,0;Y取2,X取2,1,0
由
得的概率分布为
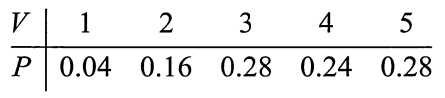
(3)
例如求U=2的概率分布,那么X取2,Y取2,3,;Y取2,X取2,3,4,5
由
得的概率分布
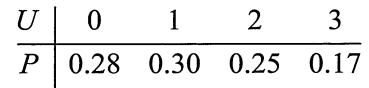
(4)
由
得 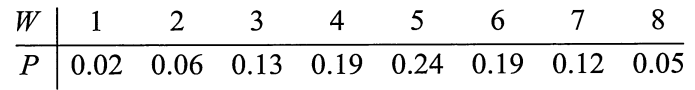
2.二维连续型随机变量函数的分布
设二维随机变量的联合概率密度为
,求
的概率密度。
方法一:分布函数法(三大步)
(1)设的分布函数为
,则
。
(2)求在
的正概率密度区域的值域
,讨论
。
当时,
;
当时,
;
当时,
。
(3)的概率密度为
。
方法二:卷积公式(四则运算)
(1)设(
),则
其中,,
,
,
。
(2)设,则
。
(3)设,则
;设
,则
。
总结:卷积公式
先确定E的范围,再任取z,沿x轴正方向穿针,确定x的范围
其他
3.★一离散一连续随机变量函数的分布
已知离散型随机变量的概率分布与连续型随机变量
的概率密度,
求的分布。
利用分布函数法,由全概率公式,对的所有取值展开计算。
4.最值函数的分布
设相互独立,分布函数分别为
,则
的分布函数为
。
的分布函数为
求逆
独立
求逆
。
特别地,若相互独立同分布,
分布函数为,
则
