当前位置：首页 > news >正文

B-树分析

news 2025/11/16 5:32:10

绪论

伸展树十年考了 8 道题，说明这个考点是一个重要的考点。

双层伸展实例分析

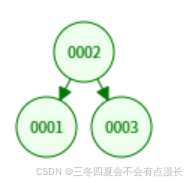
在这里插入图片描述
假设本来是这么一个伸展树，然后我们查找 3 ，双层伸展之后会变成什么样子呢。

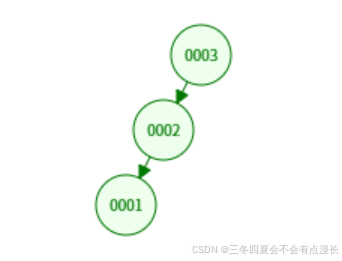
在这里插入图片描述

会变成这个样子，就是对根节点做逆时针旋转，也就是 zag 操作。我对 zig 操作稍微熟悉一些。对这个 zag 操作没有那么熟悉。这个 zag 操作，实际上就是，v 的右孩子不变，左孩子变成 p ，然后其他的不变。假设就是只有 v 和 p ，没有所谓的 g.

经过上面的实例分析，也就是说，伸展树查找之后，伸展树的高度是有可能提升的。

伸展树分摊时间复杂度的问题

假设理想随机的情况，伸展树的分摊时间复杂度是 $O (l o g n)$

假设满足局部性，那么伸展树的分摊时间复杂度是 $O (1)$

这里说明一下为啥满足局部性原理，分摊时间复杂度就是常数呢。因为，根据极限的抓大头原理，访问的节点数 k 和原来伸展树的规模 n 相对于巨大的，趋近于无穷大的 m 来说都可以视为常数。m 表示的是一个巨大的访问次数。就是对着 k 个确定的节点，不断地访问，有点类似于我们考察一个具体的重要考点，不断地考。那么总的时间复杂度就是 $O (m l o g k + n l o g n)$ ，抓大头之后就是 $O (m l o g k)$ ，分摊之后就是 $O (l o g k)$ ，k 相对于 m 就是一个常数，所以我们认为这个满足局部性原理的时候，时间复杂度分摊意义下就是 $O (1)$

伸展树的势能问题

总体的势能不可能超过 $O (n l o g n)$ ，很容易分析出来。就是高度越大，势能越大。单链的时候势能达到巅峰。此时，套用一下势能的公式，就是每个节点作为根节点的规模，连乘起来，取一个对数，考虑单链的情况，就是 $l o g n!$ ，用斯特林公式，可以证明这个和 $O (n l o g n)$ 是同级别的。

单链观察可以发现，实际上，zag 操作就是孩子节点的右孩子不变，把孩子节点提升上去。然后对于数字比较大的题，可以用几个比较小的数字，找一下规律。

双阶乘

约分之后是双阶乘的形式，实际上就是隔一项的连乘，比如， $2023!! = 2023 * 2021 * 2019 * ... * 3 * 1$

总结

感觉伸展树主要就是知道这个伸展的过程就可以了。实际上并不难。今年要是考一个类似的势能分析的题，价值 4 分，就爽死了。25 年伸展树这个单一的知识点，考察了两个题，总共考了 5 分。伸展树看来是绝对的考试重点呀。

B-树

看了一下真题，感觉还是比较困难。。。其实也不难，就是套公式，就是公式的每个式子的含义没有完全搞清楚。我深刻反思了一下，我之前的学习过程。也不是所有科目，其实之前复习数学还是复习得挺好的，每个题都总结总结，然后慢慢来。就是之前复习专业课的时候，看一遍网课就完事，也没有做题，实际上也没啥题目可以做的。还是得每个题都分析分析，这样才能形成自己的逻辑。从今天到考研的那天，还是有一些时间的。我尽量把遇到的每个题都总结和分析一下。这样才能实打实地提升自己的能力。应试实际上也是需要硬实力的。

最重要的真题就是 25 年的真题吧。感觉四个科目最重要的资料就是 25 年的真题，还有往年的真题。

引入

为什么要引入 B 树呢，因为以前，内存小，但是应用也小，现在内存变大了，但是相应的，应用增长的速度更快。也就是说，跟不上这个所谓的变化。道高一尺魔高一丈。大概就是这个感觉。

思想就是尽量少做 IO ，尽量一次 IO 尽可能多地把数据从外存读到内存，我们有一个共识，就是内存的速度大于外存，cache 的速度大于内存。

循环左移

感觉是一个还算一般的考点。就是假设我们需要循环左移几位数字，有什么比较高级的，效率比较高得算法吗。有一个思路就是，交换三次。

第一次，把左边的 k 个数字进行一个翻转。比如说，本来是 0123，翻转之后变成 3210.

第二次，把右边剩下的数字进行一个翻转。比如说，本来是 4567，翻转之后变成 7654.

第三次，把所有的数字进行一个翻转。经过前面两次翻转之后，现在的向量是 32107654, 再进行一次翻转，得到的是，45670123, 最最开始，向量是 01234567, 观察可以发现，确实是实现了循环左移的一个效果。

这个也非常巧妙。要是今年考一个这个算法题就好了。这将近 20 分我就拿下了。

B 树的结构

d 代合并成一个超级节点。啥意思呢，就是说类似于思维导图吧。m 路表示 $2^d$ 路。也就是说，多少路和多少代，两者是有一个数量关系的。B 树是一个平衡的多路搜索树。关键码有 $m - 1$ 个。也就是说，节点总数是 $m - 1$ 个？

比如说 3 个关键码，这个时候， $m = 4$ ，那么根据 $m=2^d$ 可以算出来， $d = 2$ ，也就是说，3 个关键码合并成为一个超级节点，这个超级节点有 4 个分支，有 4 个分支，说明有 $m = 4$ 路。路就是有多少个分支的意思。

进行 IO 操作需要的时间，大于直接访问内存的时间。所以我们为了提高计算的效率，希望尽可能减少 IO 次数。宁愿 1000 次访问内存，也不愿意进行一次 IO 。从考试的角度来看，宁愿把重点的知识点练习 1000 次，也不愿意在非重点上面练习一次。把重要的知识点反复的练习就是最重要的应试策略。

$log_{256}10^9<4$ ，这里我们是假设 m = 256, 也就是说，假设一个超级节点有 256 个分支，这个时候可以显著地降低 IO 次数。

m 阶 B 树表示的是，m 路的完全平衡搜索树。实际上就是和二路作一个区分。

B 树的高度问题

B 树的高度一定要算上外部节点的。B 树的高度一定要算上外部节点的。B 树的高度一定要算上外部节点的。外部节点是没有关键码信息的。

后面的东西稍微有点没看懂了。 $(⌈m2⌉,m)(\lceil\frac{m}{2}\rceil,m)$ -树。这样子来表示啥东西。。。感觉应该是一个相关的结论。就是记住这个关键码和相对应的路数的大小关系就可以了。我感觉数据结构里面很多这种相关的东西。

也就是说，有 $n≤m−1n\le m-1$ 个关键码。有 $n+1≤mn+1\le m$ 个分支。实际上这里的数学关系，移动一下就出来了。m 还是表示所谓的路数，或者就是分支数目。然后关键码是啥意思呢，就是比如说 m = 4, 然后就是 4 路分支，3 个关键码构成一个超级节点。分支数目不能太少。树根的分支数目需要大于 2，表示分支至少是 2 个分支，有点没看懂。还有分支必须大于 $⌈m2⌉\lceil\frac m 2\rceil$ 也有点没看懂。奥。看懂了。这里的表示为 $(⌈m2⌉,m)−(\lceil\frac{m}{2}\rceil,m)-$ 树表示的是分支数目取 $[⌈m2⌉,m][\lceil\frac{m}{2}\rceil,m]$ 这个区间的数字。还是非常非常有意思的。

为了不出现意外，我们最好表示的时候把外部节点也考虑进去，防止因为紧张之类的原因，导致自己分析不了这个所谓的 B-树的高度，因为外部节点肯定是要算到 B-树的高度里面去的。

关键码和分支的关系

我们观察可以发现，分支的个数是 $⌈m2⌉≤n+1≤m\lceil\frac{m}{2}\rceil\le n+1\le m$ ，关键码的数目是 $⌈m2⌉−1≤key≤m−1\lceil\frac{m}{2}\rceil -1\le key \le m-1$

今天的目标就是把 B-树和红黑树突破了。突破完了之后再整理整理。每天复习复习。就可以了。

5 阶 B- 树和 5 叉树的区别

实际上虽然考试也没有考察过这个知识点，但是这两者还是有区别的。就是 5 阶 B-树并不一定需要 5 叉， $⌈52⌉=3\lceil\frac{5}{2}\rceil=3$ ，也就是说，3，4，5 叉都符合 5 阶 B-树的这么一个定义。

B-树是模拟内存访问数据，如果内存里面数据是缺失的，那么需要进行 IO 操作访问外存，如果外存里面也没有这个数据，表示查找失败。否则就是查找成功。然后 B-树也是类似于二叉树的情况，左孩子更小，右孩子更大。

如果给一个 $(3, 5) -$ 树，表示这个是一个 5 阶 B-树。那么，关键码个数就小于等于 4，分支个数就是 3，4，5 里面取值。B-树里面进行查找是超级节点内部是从左到右顺序查找的。把超级节点视为一个节点来判断就可以了。这就是所谓的整体法吗。

我们约定根节点常驻 RAM random access memory ，实际上就是内存。随机存取存储器。

B 树的高度

这个是一个公式。感觉还是得记忆一下。要是记不住考场上还是有点无奈的。今年考一个 B-树的高度的填空题好不好！！！

$log⁡m(N+1)≤h≤1+⌊log⌈m2⌉N+12⌋\log_m(N+1)\le h \le 1+\lfloor log_{\lceil\frac{m}{2}\rceil}\frac{N+1}{2}\rfloor$

高度的推导过程，有点看不懂，这种证明确实我也不大愿意看。考试又不考。考了也是自己拿不到分数的部分吧。我感觉自己就是把所谓的套路的，死记硬背的东西搞熟练就算达到目标了。毕竟也不是说想要专业课拿多高的分数。90 分对于专业课来说就是一个完全够用的分数了。不需要说硬是往里面钻。并且 25 反馈还说押题押中了 50 分左右的内容呢。那么，我按照局部性原理来考虑。我吃透模拟卷和真题，至少可以拿到 50 分的原题，我吃透真题怎么也能帮自己把那个 40 分补上吧。

B-树插入新的关键码可能产生分裂

这么复杂么。我有点害怕了。这些数据结构设计得有些过于巧妙了。我有点害怕。上题吧。把那些题目练习得非常熟练就完事了。

看了一下 ppt 内容。确实还是挺多的呢。比较抽象的知识点。如果关键码数目超过了限制，就把最中间的关键码分裂上去，如果是偶数个关键码，就把中间偏右边的关键码分裂上去。

如果是 6 个节点，那么，就是把秩为 3 的关键码分裂出去。也就是第四个关键码。如果是 5 个节点，那么就是把秩为 2 的关键码分裂出去。用公式表示就是 $⌊m2⌋\lfloor\frac{m}{2}\rfloor$ ，效果上面就是向下取整。

上溢可能持续发生，逐层向上传播。这么秀。然后就是最极端的情况就是传播到根节点。有点没看懂这个网课和 ppt 的逻辑。

听了一下一个具体的例子。现在感觉懂了。这个我感觉完全懂了。就是每次让最中间的，分裂上去。当然前提是这个插入的关键码，使得整个的关键码数目超过了 m - 1 这个限制。

B-树的删除

需要是叶子节点。不是叶子节点就要交换到叶子节点。我们感觉知识点抽象是因为这个东西我们不熟悉，要是用一个具体的例子来帮助理解，肯定是可以分析清楚了的。

删除操作必须保证原来 B-树的性质，至少有一个性质就是中序遍历是有序的。也就是左孩子比父亲小，右孩子比父亲大。我理解不上去。呜呜呜。

还是看例子来分析分析。自己硬看结论还是太困难了。假设左兄弟和右兄弟都不够借，实际上这里说的借，意思是说，借了之后依然满足关键码个数 $⌈m2⌉−1,m−1\lceil\frac{m}{2}\rceil-1,m-1$ 这个范围。否则不够借，就合并，用父节点的关键码和孩子节点的关键码进行合并。删除之前是满足 B-树的性质的。我们现在就是想要删除之后依然满足 B-树的性质。