P11096 体育课 top51goc CSP2025模拟第二次第二题题解

———————————————————————————————

题面如上
大体意思就是:
有nnn个元素,你可以选择lll和rrr两个位置(1≤l≤r≤n1\leq l\leq r\leq n1≤l≤r≤n),在这两个位置所构成的区间内(l≤i≤rl\leq i\leq rl≤i≤r)的所有元素将从左往右升序排序,然后求每两个元素排序后的最大距离的和
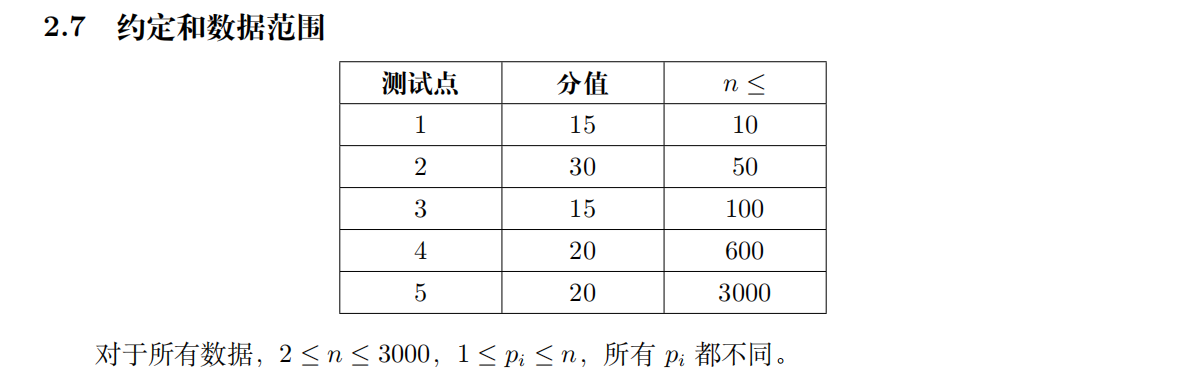
由于(1≤l≤30001\leq l\leq 30001≤l≤3000)
我们只需要双重循环两两遍历时,将找iii和jjj两个人的最大距离的时间复杂度降到O(1)O(1)O(1)
试想以下思路:
第一种排序情况便是将所有元素都选中,此时两者的距离变为 ∣p[i]−p[j]∣|p[i]-p[j]|∣p[i]−p[j]∣但是这并不一定的最优情况。
所以又有以下两种
对于iii这个人来说,要与jjj的距离更远,由于(i≤ji\leq ji≤j)就要让更多的元素到 (i+1)∼(j−1)(i+1) \sim (j-1)(i+1)∼(j−1)的这个区间,所以让1∼i1\sim i1∼i的元素都选中(l=1,r=i)(l=1,r=i)(l=1,r=i)参与排序,通过升序排序把前面比他大的元素到(i+1)∼(j−1)(i+1) \sim (j-1)(i+1)∼(j−1)这个区间里,而这样,他远离jjj的距离就是原本在 1∼(i−1)1\sim (i-1)1∼(i−1) 区间之内的比他大的数的个数
反之对于jjj这个人来说,要与iii的距离更远,由于(j≥ij\geq ij≥i),所以让更多的元素到&(i+1) \sim (j-1)&的这个区间,所以让j∼nj\sim nj∼n这个区间里的所有元素都选中(l=j,r=n)(l=j,r=n)(l=j,r=n)都参与排序,升序排序会将它原本后面小于它的元素排到他的前面,而这样他远离iii的距离就是原本在 (j+1)∼n(j+1)\sim n(j+1)∼n区间之内比他小的元素的个数
而每两个人之间的最大距离就是这三种情况里的最优解
为了O(1)O(1)O(1)查询1∼(i−1)1\sim (i-1)1∼(i−1)和(j+1)∼n(j+1)\sim n(j+1)∼n这两个区间里的符合条件的元素个数
我们使用两个标记数组来预处理1∼(i−1)1\sim (i-1)1∼(i−1) 区间之内的比p[i]p[i]p[i]大的数的个数
和 (j+1)∼n(j+1)\sim n(j+1)∼n区间之内比p[j]p[j]p[j]小的元素的个数
预处理大概框架(伪代码)
for i 1 n
{for j 1 i-1if p[j] > p[i]cnt1[i] + 1for j i + 1 nif p[j] < p[i]cnt2[i] + 1
}
最后就是求和了
在 排序1∼i1\sim i1∼i这个区间 和 排序 j∼nj\sim nj∼n这个区间 取最优解 再加上原本jjj与iii的距离
也就是maxmaxmax(1∼(i−1)1\sim (i-1)1∼(i−1) 区间之内的比p[i]p[i]p[i]大的数的个数,(j+1)∼n(j+1)\sim n(j+1)∼n区间之内比p[j]p[j]p[j]小的元素的个数) 再加上原本jjj与iii的距离
也就是max(cnt1[i],cnt2[j])+(j−i)max(cnt1[i],cnt2[j])~+~(j-i)max(cnt1[i],cnt2[j]) + (j−i)
还要和将所有元素都选中的这种情况进行最优解比较
也就是max(max(cnt1[i],cnt2[j])+(j−i),∣p[i]−p[j]∣)max(max(cnt1[i],cnt2[j])~+~(j-i)~,~|p[i]-p[j]|)max(max(cnt1[i],cnt2[j]) + (j−i) , ∣p[i]−p[j]∣)
求和大概框架(伪代码)
for i 1 n-1
{for j i+1 n{//为了方便书写// 定义一个temp保存1、2两种情况的最优解temp = max(cnt1[i], cnt2[j]) + (j - i)temp = max(temp, abs(p[i] - p[j])) //与全选的情况最优解比较ans + temp }
}