磁共振成像原理（理论）28：饱和恢复序列 (Saturation-Recovery Sequence)

引言

图像对比度是磁共振成像中的重要参数，因为人类视觉系统不擅长判断绝对亮度值。如下图所示，两个中间小方块的实际强度相同，但右侧的看起来更亮，这说明了对比度感知的复杂性。

图像对比度被定义为：图像强度差异的函数。具体而言，设$I_A$和$I_B$分别表示组织A和B的图像强度，${\mathcal{C}}_{AB}$为它们的对比度指数，则对比度定义为：
$${\mathcal{C}}_{AB}=\frac{|I_A-I_B|}{I_{\text{ref}}}\text{\hspace{1em}(7.1)}$$

其中$I_{\text{ref}}$为归一化参考值（通常取白质或灰质的平均强度）。从公式(7.1)可以看出，增强图像对比度需要最大化不同组织间的图像强度差异。这也是序列设计的一个目标之一。

在磁共振成像中，图像强度$I$是自旋密度$\rho$、弛豫时间$T_1$、$T_2$、$T_2^{\ast }$、扩散系数$D$等多参数的函数。因此，对比度可表示为：
$${\mathcal{C}}_{AB}=f(\rho ,T_1,T_2,T_2^{\ast },D,\dots )\text{\hspace{1em}(7.2)}$$

函数$f$的具体形式取决于数据采集序列。通过选择突出特定效应的参数，可获得近似对比度：

• 当$T_1$效应占主导时，得到$T_1$对比度：
  $${\mathcal{C}}_{AB}\approx f(T_1)\text{\hspace{1em}(7.3)}$$
• 当自旋密度效应占主导时，得到自旋密度对比度：
  $${\mathcal{C}}_{AB}\approx f(\rho )\text{\hspace{1em}(7.4)}$$
• 当$T_2$效应占主导时，得到$T_2$对比度：
  $${\mathcal{C}}_{AB}\approx f(T_2)\text{\hspace{1em}(7.5)}$$

饱和恢复序列

基本饱和恢复序列由一系列等间隔的90°脉冲组成，如下图所示。脉冲间隔时间称为重复时间$T_R$。该序列可简写为：
$$(90^{\circ }-T_R{)}_N\text{\hspace{1em}(7.6)}$$
其中$N$为90°脉冲的应用次数。

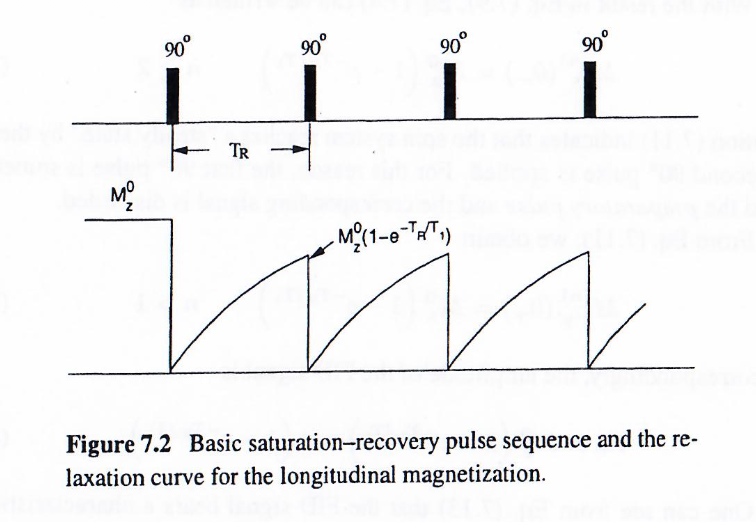
为分析该序列的图像对比特性，需推导信号与序列参数的关系表达式。设$M_{z^{\prime }}^{(n)}(0_{-})$和$M_{z^{\prime }}^{(n)}(0_{+})$分别表示第$n$个90°脉冲前后的纵向磁化强度，初始条件为：
$$\{\begin{array}{l}{M}_{z^{\prime }}^{(1)}(0_{-})=M_z^0\\ M_{z^{\prime }}^{(1)}(0_{+})=0\end{array}\text{\hspace{1em}(7.7)}$$

根据弛豫方程（式3.122）
$$\{\begin{array}{l}{M}_{x^{\prime }{y}^{\prime }}(t)=M_{x^{\prime }{y}^{\prime }}(0_{+})e^{-t/T_2}\\ M_{z^{\prime }}(t)=M_z^0(1-e^{-t/T_1})+M_{z^{\prime }}(0_{+})e^{-t/T_1}\end{array}\text{\hspace{1em}(3.122)}$$

对于$n>1$，也就是第n个脉冲前$M_{z^{\prime }}^{(n)}(0_{-})$，发生在第n-1个脉冲作用后$M_{z^{\prime }}^{(n-1)}(0_{+})$的$T_R$时刻，将$M_{z^{\prime }}(0_{+})\to M_{z^{\prime }}^{(n-1)}(0_{+}),t\to T_R$，可得：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0\left(1-e^{-T_R/T_1}\right)+M_{z^{\prime }}^{(n-1)}(0_{+})e^{-T_R/T_1}\text{\hspace{1em}(7.8)}$$

该激发序列通常满足饱和条件：
$$M_{z^{\prime }}^{(n)}(0_{+})=0(n\ge 1)\text{\hspace{1em}(7.9)}$$

此条件在$T_R\gg T_2$时成立。饱和条件意味着前一个90°脉冲产生的横向磁化在下一个脉冲应用前已完全衰减。因此不会有横向磁化被90°脉冲转到纵向，基于式(7.9)，式(7.8)可改写为：
$$M_{z^{\prime }}^{(n)}(0_{-})=M_z^0\left(1-e^{-T_R/T_1}\right)(n\ge 2)\text{\hspace{1em}(7.11)}$$

这表明自旋系统在第二个90°脉冲前已达到稳态。因此，第一个90°脉冲常称为预备脉冲，其对应信号通常被舍弃。因为第一个脉冲产生的信号幅度正比于 $M_z^0$，而稳态信号幅度正比于 $M_z^0(1-e^{-T_R/T_1})$：
$$\begin{array}{rl}{S}_1& \propto M_z^0\\ S_n& \propto M_z^0(1-e^{-T_R/T_1})(n\ge 2)\end{array}$$

而对于长 $T_1$ 组织，当 $T_R\ll T_1$ 时：
$$(1-e^{-T_R/T_1})\ll 1\text{\hspace{1em}()}$$
第一个信号幅度远大于稳态信号幅度，如果混合使用会造成严重的图像伪影。

回到正文，由式(7.11)可得横向磁化强度：
$$M_{x^{\prime }{y}^{\prime }}^{(n)}(0_{+})=M_z^0\left(1-e^{-T_R/T_1}\right)(n>1)\text{\hspace{1em}(7.12)}$$

相应的FID信号幅度为：
$$A_f\propto M_z^0\left(1-e^{-T_R/T_1}\right)\propto \rho \left(1-e^{-T_R/T_1}\right)\text{\hspace{1em}(7.13)}$$

从式(7.13)可见，FID信号携带：特征性的$T_1$加权因子$(1-e^{-T_R/T_1})$。该加权因子不受后续空间信息编码和图像重建步骤影响，因此图像强度同样具有$T_1$加权特性：
$$I(\mathbf{r})=C\rho (\mathbf{r})\left[1-e^{-T_R/T_1(\mathbf{r})}\right]\text{\hspace{1em}(7.14)}$$

其中$C$为与编码和重建方法相关的比例常数。饱和恢复序列可产生自旋密度加权或$T_1$加权对比度：

• 当采用长$T_R$时，$(1-e^{-T_R/T_1})\to 1$，组织对比主要来自自旋密度差异；
• 当采用短$T_R$时，图像呈$T_1$加权，组织对比主要源于$T_1$值差异。

最优$T_R$计算

假设样本包含两种自旋密度均匀但$T_1$弛豫时间不同（$T_{1A}$和$T_{1B}$）的组织。根据式(7.14)，强度表达式为：
$$\{\begin{array}{l}{I}_A\propto {\rho }_A(1-e^{-T_R/T_{1A}})\\ I_B\propto {\rho }_B(1-e^{-T_R/T_{1B}})\end{array}\text{\hspace{1em}(7.16)}$$

当${\rho }_A={\rho }_B$时，对比度为：
$${\mathcal{C}}_{AB}\propto |I_A-I_B|=C\left(e^{-T_R/T_{1B}}-e^{-T_R/T_{1A}}\right)\text{\hspace{1em}(7.17)}$$

最优$T_R$值需满足：
$$\frac{\partial {\mathcal{C}}_{AB}}{\partial T_R}=C\left(\frac{1}{T_{1A}}{e}^{-T_R/T_{1A}}-\frac{1}{T_{1B}}{e}^{-T_R/T_{1B}}\right)=0\text{\hspace{1em}(7.18)}$$

解得：
$$T_R^0=\frac{\ln \left(\frac{T_{1A}}{T_{1B}}\right)}{\frac{1}{T_{1B}}-\frac{1}{T_{1A}}}\text{\hspace{1em}(7.19)}$$
而当${\rho }_A\ne {\rho }_B$时，组织A和B之间的对比度定义为它们图像强度的绝对差值：
$${\mathcal{C}}_{AB}=|I_A-I_B|=C\cdot \left|{\rho }_A(1-e^{-T_R/T_{1,A}})-{\rho }_B(1-e^{-T_R/T_{1,B}})\right|\text{\hspace{1em}()}$$

为了最大化对比度 ${\mathcal{C}}_{AB}$，需要找到使 $|I_A-I_B|$ 取最大值的 $T_R$ 值。不失一般性，假设 $I_A>I_B$（如果相反，只需交换A和B的标签），因此可以去掉绝对值符号：
$${\mathcal{C}}_{AB}=C\left[{\rho }_A(1-e^{-T_R/T_{1,A}})-{\rho }_B(1-e^{-T_R/T_{1,B}})\right]\text{\hspace{1em}()}$$

定义目标函数：
$$f(T_R)={\rho }_A(1-e^{-T_R/T_{1,A}})-{\rho }_B(1-e^{-T_R/T_{1,B}})\text{\hspace{1em}()}$$

对目标函数求导并令导数为零：
$$\begin{array}{rl}\frac{df(T_R)}{d{T}_R}& ={\rho }_A\cdot \frac{1}{T_{1,A}}{e}^{-T_R/T_{1,A}}-{\rho }_B\cdot \frac{1}{T_{1,B}}{e}^{-T_R/T_{1,B}}=0\\ {\rho }_A\cdot \frac{1}{T_{1,A}}{e}^{-T_R/T_{1,A}}& ={\rho }_B\cdot \frac{1}{T_{1,B}}{e}^{-T_R/T_{1,B}}\end{array}$$

将方程(7.19)两边取自然对数：
$$\ln \left({\rho }_A\cdot \frac{1}{T_{1,A}}\right)-\frac{T_R}{T_{1,A}}=\ln \left({\rho }_B\cdot \frac{1}{T_{1,B}}\right)-\frac{T_R}{T_{1,B}}\text{\hspace{1em}()}$$

整理项：
$$\frac{T_R}{T_{1,B}}-\frac{T_R}{T_{1,A}}=\ln \left({\rho }_B\cdot \frac{1}{T_{1,B}}\right)-\ln \left({\rho }_A\cdot \frac{1}{T_{1,A}}\right)\text{\hspace{1em}()}$$

提取公因子并简化：
$$T_R\left(\frac{1}{T_{1,B}}-\frac{1}{T_{1,A}}\right)=\ln \left(\frac{{\rho }_B}{{\rho }_A}\cdot \frac{T_{1,A}}{T_{1,B}}\right)\text{\hspace{1em}()}$$

对于自旋密度不同的两种组织，饱和恢复序列中最优重复时间的通用解为：
$$T_R^o=\frac{\ln \left(\frac{{\rho }_B{T}_{1,A}}{{\rho }_A{T}_{1,B}}\right)}{\frac{1}{T_{1,B}}-\frac{1}{T_{1,A}}}$$