2025-11-12[第三大的数、将x减到0的最小操作数]

题目链接

第三大的数

题目描述

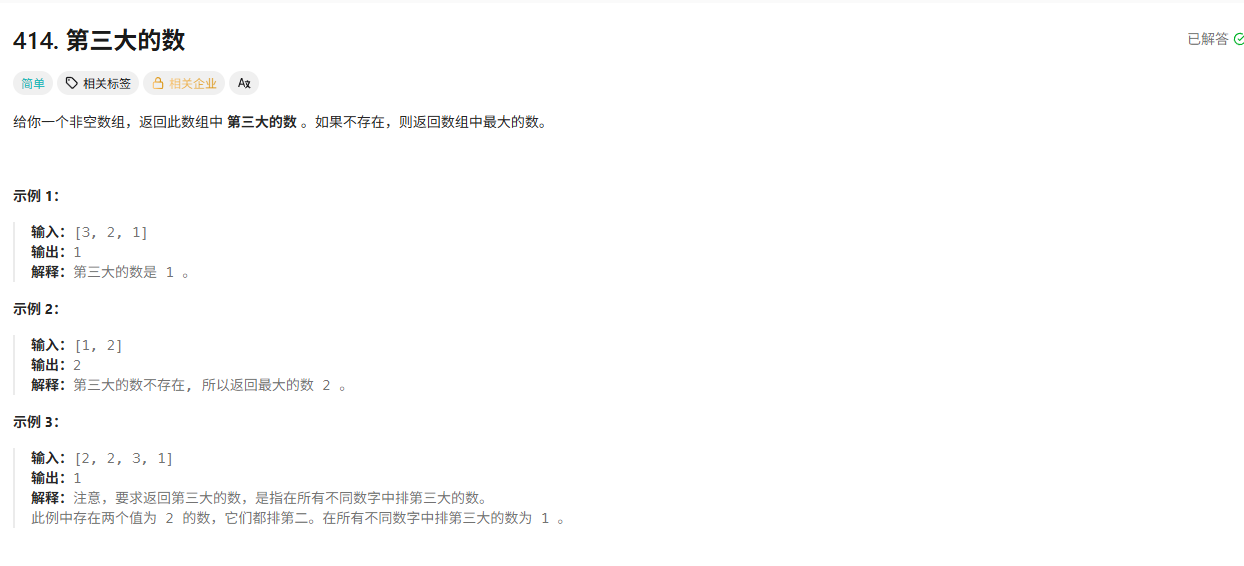
题目解析

思路

1. 去重处理：由于题目要求第三大的数是指所有不同数字中排第三大的数，因此首先需要去除数组中的重复元素。
2. 排序处理：对去重后的元素进行排序，以便快速找到第三大的元素。
3. 判断与返回：根据去重后的元素数量判断是否存在第三大的元素。如果元素数量不少于 3，则返回第三大的元素（即排序后倒数第三个元素）；否则返回最大的元素（即排序后最后一个元素）。

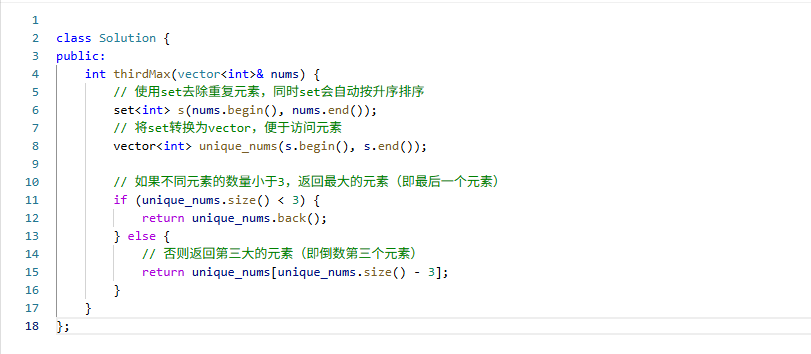
解释

1. 去重与排序：使用set容器对数组进行处理，set会自动去除重复元素并按升序排序，这一步同时完成了去重和排序的工作。
2. 转换为向量：将set转换为vector，以便更方便地通过索引访问元素。
3. 判断元素数量：检查去重排序后的元素数量。如果数量小于 3，说明不存在第三大的元素，返回最大元素（即向量的最后一个元素）；如果数量不少于 3，则返回第三大的元素（即向量中倒数第三个元素）。

这种方法简洁高效，充分利用了set容器的特性，使得去重和排序过程变得简单，整体时间复杂度主要由set的插入操作决定，为 O (n log n)，其中 n 是数组的长度。

---

题目链接

将x减到0的最小操作数

题目描述

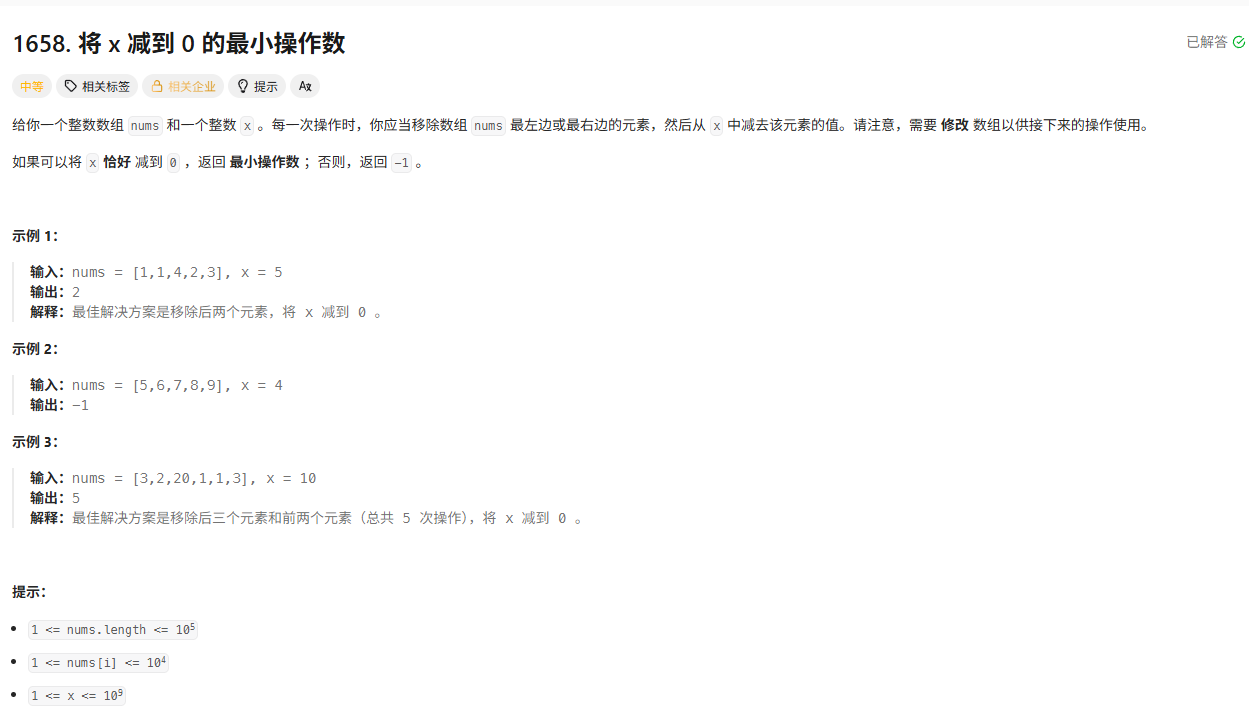
题目解析

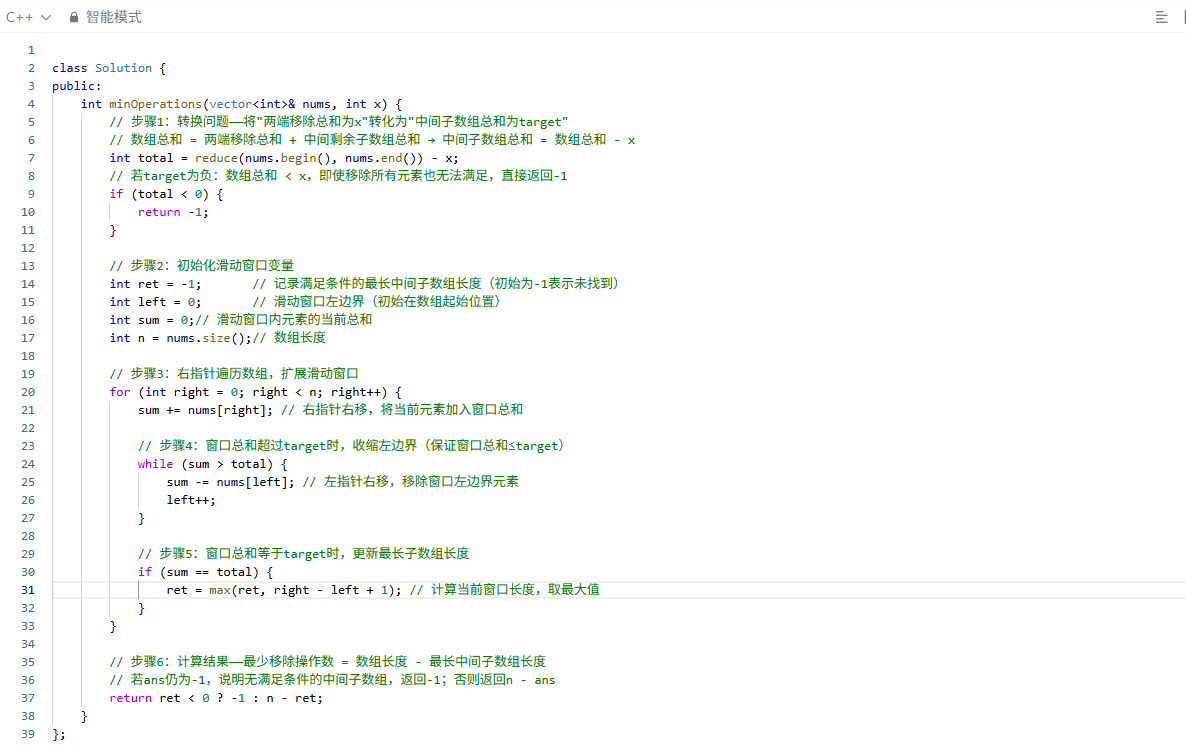
核心原理与问题转化

1. 问题本质转换（关键洞察）

• 原问题：从数组两端移除元素，使移除元素总和为x，求最少移除次数。
• 转化后：寻找数组中间连续子数组，使子数组总和为target = 数组总总和 - x，求最长这样的子数组。
• 为什么转化？
  • 因为 “两端移除最少元素” 等价于 “中间保留最多元素”（总数固定），将最小操作数问题转化为最长子数组问题，更易用滑动窗口求解。

 滑动窗口适用条件

• 数组元素均为正数（题目隐含条件，否则滑动窗口逻辑不成立）：
  • 当窗口总和超过target时，收缩左边界必然使总和减小；
  • 当窗口总和小于target时，扩展右边界必然使总和增大。
• 时间复杂度：O(n)（左右指针各遍历数组一次，无嵌套循环）。
• 空间复杂度：O(1)（仅用常数额外空间）。

核心思想

• 通过问题转化将两端移除问题转化为中间子数组问题，利用滑动窗口高效寻找最长满足条件的子数组。
• 滑动窗口的核心是 “扩展右边界、收缩左边界”，保证窗口总和始终≤target，从而找到总和等于 target 的最长窗口。