Leetcode 54

1 题目

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

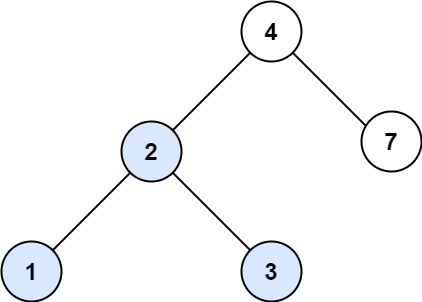
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

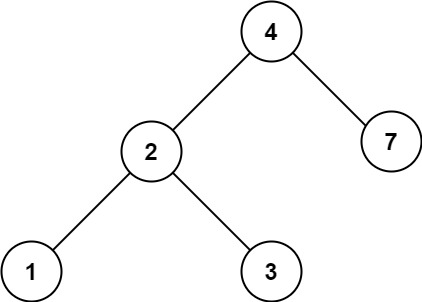
输入：root = [4,2,7,1,3], val = 5
输出：[]

提示：

• 树中节点数在 [1, 5000] 范围内
• 1 <= Node.val <= 107
• root 是二叉搜索树
• 1 <= val <= 107

2 代码实现

如果是一般的二叉树，寻找特定 val 的节点不是很难

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == nullptr){return nullptr;}if(root -> val == val){return root;}TreeNode* left = searchBST(root -> left ,val);TreeNode* right = searchBST(root -> right ,val);return left == nullptr ? right : left ;}
};

结合BST的特性优化代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == nullptr){return nullptr;}if(root -> val == val){return root;}if(root -> val > val){return searchBST(root -> left ,val);}else{return searchBST(root -> right ,val);}}
};

一开始写犯了错误，并且要结合BST特性实现剪枝

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == nullptr){return nullptr;}if(root -> val){return root;}TreeNode* left = searchBST(root -> left ,val);TreeNode* right = searchBST(root -> right ,val);return left == nullptr ? right : left ;}
};

你的代码存在逻辑错误，主要问题在于判断条件和搜索逻辑上，具体分析如下：

错误原因

1. 判断条件错误代码中 if(root -> val) 这一行的逻辑有问题。这个条件实际判断的是 root->val 是否为非 0 值（在 C++ 中，非 0 值会被视为true），而不是判断当前节点的值是否等于目标值val。正确的判断应该是 if(root->val == val)，只有当当前节点的值等于目标值时，才返回该节点。

2. 搜索逻辑不符合 BST 特性二叉搜索树（BST）的特性是：对于任意节点，其左子树的所有节点值都小于该节点值，右子树的所有节点值都大于该节点值。你的代码采用了类似普通二叉树的全遍历（同时搜索左右子树），没有利用 BST 的特性进行剪枝，虽然在功能上可能 “碰巧” 找到节点，但效率低下且不符合 BST 的搜索逻辑。正确的做法是：

   • 若当前节点值等于val，返回当前节点；
   • 若当前节点值大于val，则只需搜索左子树；
   • 若当前节点值小于val，则只需搜索右子树。

修正后的代码

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* searchBST(TreeNode* root, int val) {if (root == nullptr) {return nullptr; // 空节点，返回null}if (root->val == val) {return root; // 找到目标节点，返回} else if (root->val > val) {return searchBST(root->left, val); // 目标值更小，搜索左子树} else {return searchBST(root->right, val); // 目标值更大，搜索右子树}}
};

总结

你的代码主要错误是判断条件写错（漏了== val），且没有利用 BST 的特性优化搜索。修正后，代码会根据 BST 的性质高效地找到目标节点，时间复杂度为 O (h)（h 为树的高度）。

3 题目

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

一般来说，删除节点可分为两个步骤：

1. 首先找到需要删除的节点；
2. 如果找到了，删除它。

示例 1:

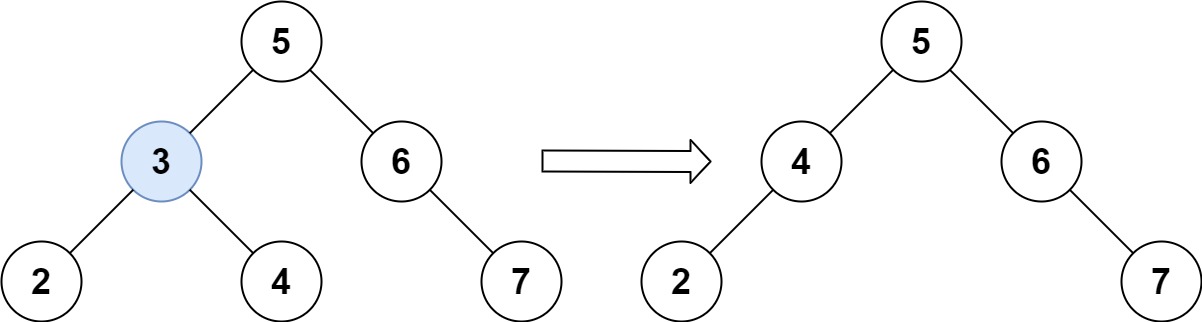
输入：root = [5,3,6,2,4,null,7], key = 3
输出：[5,4,6,2,null,null,7]
解释：给定需要删除的节点值是 3，所以我们首先找到 3 这个节点，然后删除它。
一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。
另一个正确答案是 [5,2,6,null,4,null,7]。

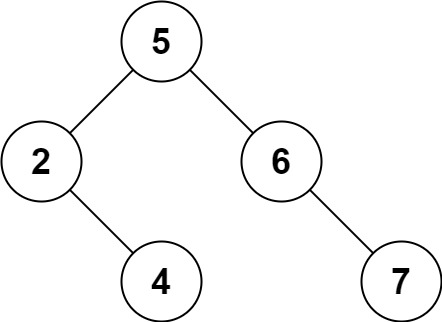
示例 2:

输入: root = [5,3,6,2,4,null,7], key = 0
输出: [5,3,6,2,4,null,7]
解释: 二叉树不包含值为 0 的节点

示例 3:

输入: root = [], key = 0
输出: []

提示:

• 节点数的范围 [0, 104].
• -105 <= Node.val <= 105
• 节点值唯一
• root 是合法的二叉搜索树
• -105 <= key <= 105

进阶： 要求算法时间复杂度为 O(h)，h 为树的高度。

4 代码实现

这道题思路很明确，先找后删。

找的过程之间根据上面的题目能学会了，但是怎么删呢？看下面的笔记讲解的很清楚。

二叉搜索树心法（基操篇） | labuladong 的算法笔记

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:TreeNode* getMin(TreeNode* node){while (node -> left != nullptr){node = node -> left ;}return node;}TreeNode* deleteHelper(TreeNode* node , int key){if (node == nullptr) return nullptr;if (node -> val > key){node -> left = deleteHelper( node -> left , key);}else if (node -> val < key){node -> right = deleteHelper (node -> right ,key);}else {if (node -> left == nullptr && node -> right == nullptr){return nullptr;}else if (node -> left == nullptr){return node -> right ;}else if (node -> right == nullptr){return node -> left ;}else{TreeNode* minNode = getMin(node -> right );node -> val = minNode -> val;node -> right = deleteHelper(node -> right ,minNode -> val);}}return node ;}
public:TreeNode* deleteNode(TreeNode* root, int key) {return deleteHelper(root ,key);}
};

删除二叉搜索树（BST）中的节点是一个经典问题，核心在于删除节点后仍需保持 BST 的特性（即对于任意节点，左子树所有节点值 < 该节点值 < 右子树所有节点值）。删除操作需根据节点的子树情况分情况处理，具体步骤如下：

一、删除节点的三种情况

假设要删除的节点为 node，根据其左、右子树是否为空，分为三种情况：

1. 节点为「叶子节点」（左、右子树均为空）

• 处理方式：直接删除该节点，无需额外操作。
• 原因：删除叶子节点不会影响其他节点的父子关系，BST 特性自然保持。

2. 节点「只有一棵子树」（左空右非空 或 右空左非空）

• 处理方式：用子树替代被删除节点的位置。
  • 若左子树为空，用右子树替代 node；
  • 若右子树为空，用左子树替代 node。
• 原因：子树的所有节点值均满足与 node 的父节点的大小关系（BST 特性保证），直接替代即可维持特性。

3. 节点「有两棵子树」（左、右子树均非空）

• 核心问题：删除节点后，需要找一个「替代节点」填补其位置，且保证替代节点的值满足 BST 特性。
• 替代节点的选择：
  • 左子树的最大值（左子树中最右侧的节点）：该值是左子树中最大的，且小于 node 的右子树所有节点值；
  • 右子树的最小值（右子树中最左侧的节点）：该值是右子树中最小的，且大于 node 的左子树所有节点值。
• 处理步骤：
  1. 找到替代节点（如右子树的最小值 successor）；
  2. 用 successor 的值覆盖 node 的值；
  3. 删除 successor 节点（此时 successor 最多只有一棵子树，按情况 1 或 2 处理）。

二、具体实现步骤（递归版）

1. 定位目标节点：根据 BST 特性，递归查找值为 val 的节点：

   • 若当前节点值 > val，递归搜索左子树；
   • 若当前节点值 < val，递归搜索右子树；
   • 若找到节点（值相等），执行删除逻辑。

2. 执行删除逻辑：按上述三种情况处理：

   • 叶子节点：返回 nullptr（父节点会忽略该节点）；
   • 单棵子树：返回非空子树；
   • 两棵子树：找替代节点，覆盖值后删除替代节点。

三、代码示例

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:TreeNode* deleteNode(TreeNode* root, int val) {if (root == nullptr) return nullptr; // 空树，直接返回// 1. 定位目标节点if (root->val > val) {// 目标在左子树，递归删除后更新左子树root->left = deleteNode(root->left, val);} else if (root->val < val) {// 目标在右子树，递归删除后更新右子树root->right = deleteNode(root->right, val);} else {// 2. 找到目标节点，执行删除逻辑if (root->left == nullptr) {// 左子树为空，用右子树替代return root->right;} else if (root->right == nullptr) {// 右子树为空，用左子树替代return root->left;} else {// 3. 左右子树均非空：找右子树的最小值（后继节点）TreeNode* successor = root->right;while (successor->left != nullptr) {successor = successor->left; // 最左侧节点即最小值}// 用后继节点的值覆盖当前节点root->val = successor->val;// 删除后继节点（后继节点最多只有右子树）root->right = deleteNode(root->right, successor->val);}}return root;}
};

四、关键说明

• 时间复杂度：O (h)，h 为树的高度（平衡 BST 为 O (log n)，极端不平衡为 O (n)）。
• 替代节点的选择：示例中用了右子树的最小值（后继），也可用左子树的最大值（前驱），逻辑类似（找左子树最右侧节点）。
• 递归的作用：递归自动处理了父节点与子树的连接关系，无需手动调整指针（删除后返回新的子树根节点，父节点直接接收）。

通过以上步骤，即可在删除节点后保持 BST 的特性。

写到一半崩溃了，不会写了，有点复杂呢

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:void findKey (TreeNode* root , int key){if (root == nullptr){return;}if (root -> val == key){deleteNode(root);}else if (root ->val > key){findKey(root -> left , key);}else(findKey(root -> right , key);)}TreeNode* deleteNode(TreeNode* node , int key){if (node == nullptr) return nullptr;if (node -> left == nullptr && node -> right == nullptr){return nullptr;}else if (node -> left == nullptr) return node -> right;else if (node -> right == nullptr) return node -> left;else{TreeNode* minNode = getMin( node-> right );node -> val =minNode -> val ;return node;}}
public:TreeNode* deleteNode(TreeNode* root, int key) {}
};//好复杂，写不来

别着急！删除 BST 节点确实有点绕，主要是要处理不同情况的节点，还要保持 BST 的特性。我们一步步来拆解，把你的代码改对，你会发现其实没那么难～

先分析你的代码问题

1. 函数设计混乱：你定义了两个deleteNode函数（重载），但逻辑没串起来，findKey找到节点后不知道怎么通知父节点更新指针。（啊没仔细看函数名...无语凝噎）
2. 删除逻辑不完整：当节点有两个子树时，只复制了最小值，却没删除那个最小值节点，导致树结构出错。
3. 入口函数未实现：public的deleteNode没写具体逻辑，无法启动整个流程。

简化思路：递归到底，让父节点 “接管”

核心思想：递归时，让当前节点的父节点直接接收删除后的子树，不用单独写findKey，直接在递归中定位并处理节点。

分 3 步走：

1. 找目标节点（利用 BST 特性，左小右大）
2. 找到后，按 3 种情况删除（叶子 / 单孩子 / 双孩子）
3. 让父节点接收处理后的子树，自动完成指针更新

修正后的代码（带详细注释）

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
private:// 辅助函数：找右子树的最小值节点（最左侧节点）TreeNode* getMin(TreeNode* node) {while (node->left != nullptr) {node = node->left;}return node;}// 递归删除节点的核心函数TreeNode* deleteHelper(TreeNode* node, int key) {if (node == nullptr) {return nullptr; // 没找到目标节点，返回空}// 1. 先定位目标节点if (node->val > key) {// 目标在左子树，递归删除后，左孩子更新为删除后的结果node->left = deleteHelper(node->left, key);} else if (node->val < key) {// 目标在右子树，递归删除后，右孩子更新为删除后的结果node->right = deleteHelper(node->right, key);} else {// 2. 找到目标节点，执行删除逻辑// 情况1：叶子节点（左右都空）if (node->left == nullptr && node->right == nullptr) {return nullptr; // 父节点会把这里设为null}// 情况2：只有右孩子else if (node->left == nullptr) {return node->right; // 父节点直接连右孩子}// 情况3：只有左孩子else if (node->right == nullptr) {return node->left; // 父节点直接连左孩子}// 情况4：有两个孩子else {// 找右子树的最小值节点（替代节点）TreeNode* minNode = getMin(node->right);// 用替代节点的值覆盖当前节点node->val = minNode->val;// 删除那个替代节点（它一定是叶子或只有右孩子）node->right = deleteHelper(node->right, minNode->val);}}return node; // 返回处理后的节点给父节点}public:TreeNode* deleteNode(TreeNode* root, int key) {return deleteHelper(root, key); // 调用辅助函数启动删除}
};

为什么这样写？

1. 递归自动处理父节点指针：比如删除左子树的节点后，node->left = 处理结果 直接让父节点的左指针指向新的子树，不用手动维护复杂的指针关系。
2. 分情况处理清晰：把 4 种情况（没找到 / 叶子 / 单孩子 / 双孩子）拆解开，每种情况逻辑简单。
3. 替代节点的处理：当有两个孩子时，找右子树最小值（或左子树最大值），复制值后再删除它，保证 BST 特性不变。

一句话总结

删除 BST 节点的关键是：找到节点后，根据子树情况用合适的节点 “填补空位”，再让递归自动帮你更新父节点的指针。多画几个例子（比如删叶子、删单孩子、删双孩子），走一遍流程就懂了～别怕，多练两次就熟练啦！