【剑斩OFFER】算法的暴力美学——山脉数组的蜂顶索引

一、题目描述

二、算法原理

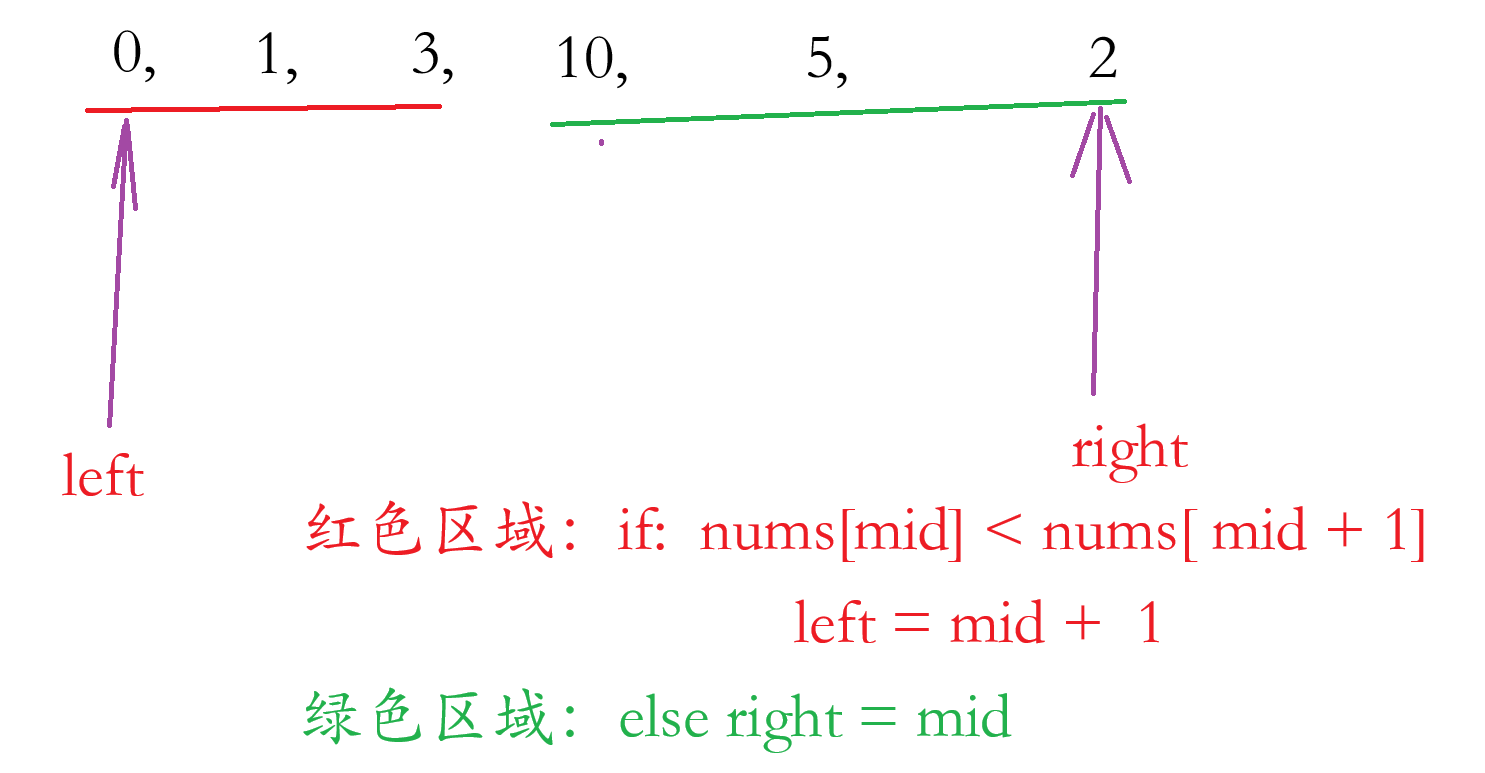
首先我们我们观察一下数组里面的数字的排列的规律：在没遇到蜂顶元素时，前面的数据的是依次变大的，而蜂顶的元素后面的数字是依次递减的，我们可以把蜂顶的元素归于这其中的一类，故而如上图一样。

如上图，我们可以假设我们求的中间点的落于红色区域，此时红色区域是没有蜂顶元素的，所以我们要让 left 移动到 mid + 1，到 [ mid + 1，right ] 去找我们要的答案。

而当我们的中间点落于绿色区域时，因为绿色里面数字包含蜂顶元素，而且是依次递减的所以，我们要让 right 移动到 mid ，不能移动到 mid - 1 ，原因 mid 有可能是蜂顶元素。这相当于求二分查找的查找最左边的元素，所以根据二次查找的查找最左边的元素的模板得：循环条件：left < tight 

求 mid 的方式：int mid = left + (right - left )/2

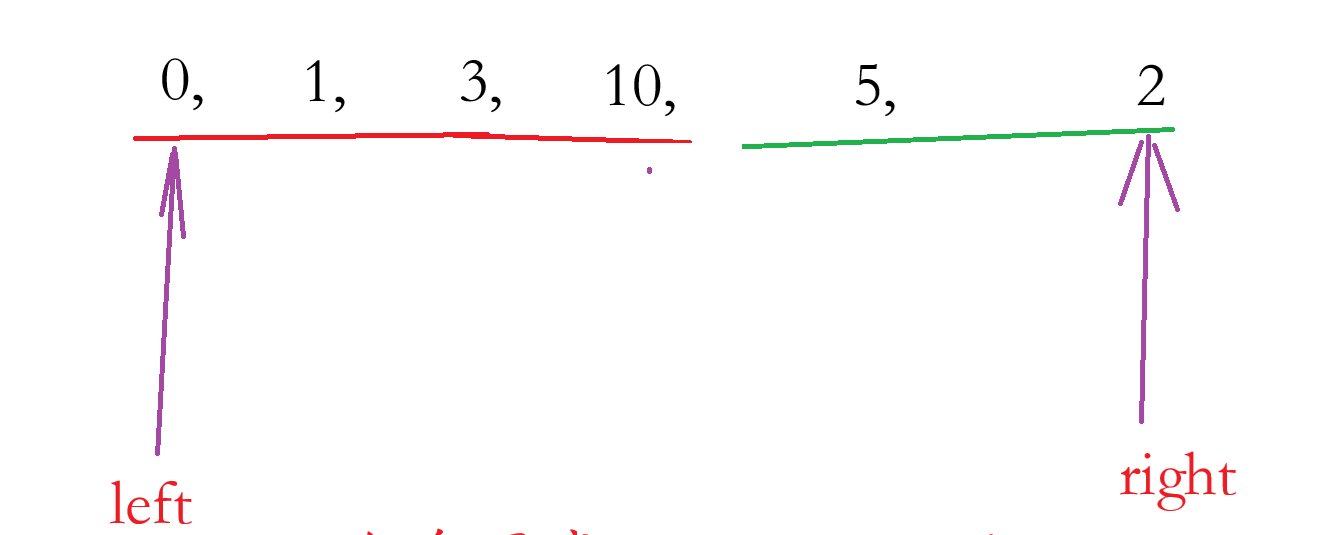
当然我们也可以把蜂顶元素归于红色区域，此时：

当 mid 落于红色区域：if( nums[mid] > nums[ mid - 1] )，此时因为红色区域包含我们要求的答案，所以我们不能让 left = mid + 1，而是：left = mid

当 mid  落于绿色区域时：else :  right =  mid - 1，因为绿色区域包含蜂顶的元素。

这和我们二分查找的查找最右端点的元素的模板一样：

循环条件：left < right

求 mid 的方式：int mid = left + (right - left + 1)/2

三、代码实现

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 1, right = arr.size() - 2;//根据题目意思，峰顶元素不可能是第一个和最后一个while(left < right){int mid = left + (right - left)/2;if(arr[mid] < arr[mid + 1]) left =  mid + 1;else right = mid;}return left;}
};

第二种方式的代码实现：

class Solution {
public:int peakIndexInMountainArray(vector<int>& arr) {int left = 1, right = arr.size() - 2;//根据题目意思，峰顶元素不可能是第一个和最后一个while(left < right){int mid = left + (right - left + 1)/2;if(arr[mid] > arr[mid - 1]) left =  mid;else right = mid - 1;}return left;}
};