跟踪导论（三）——滤波的释义位置信息的“观测+修正”

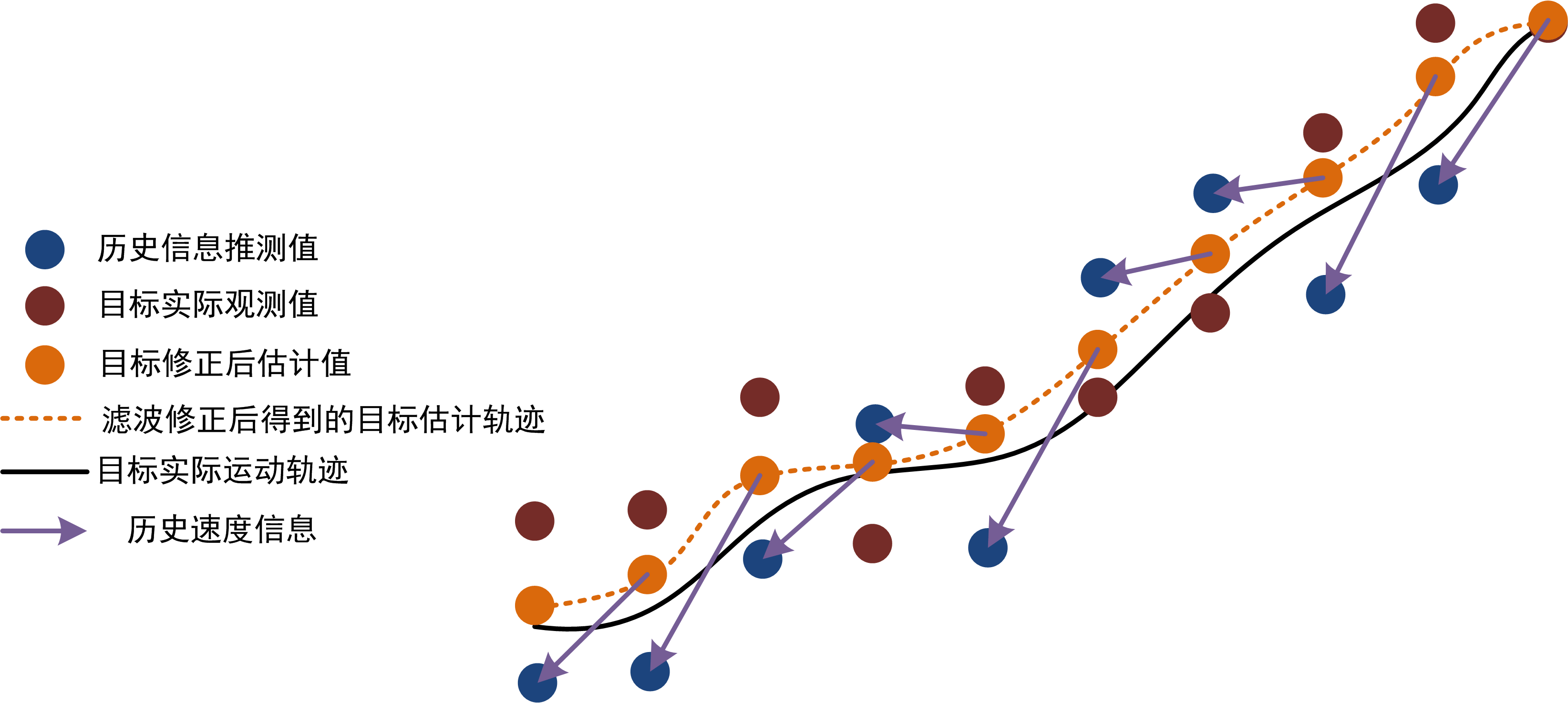
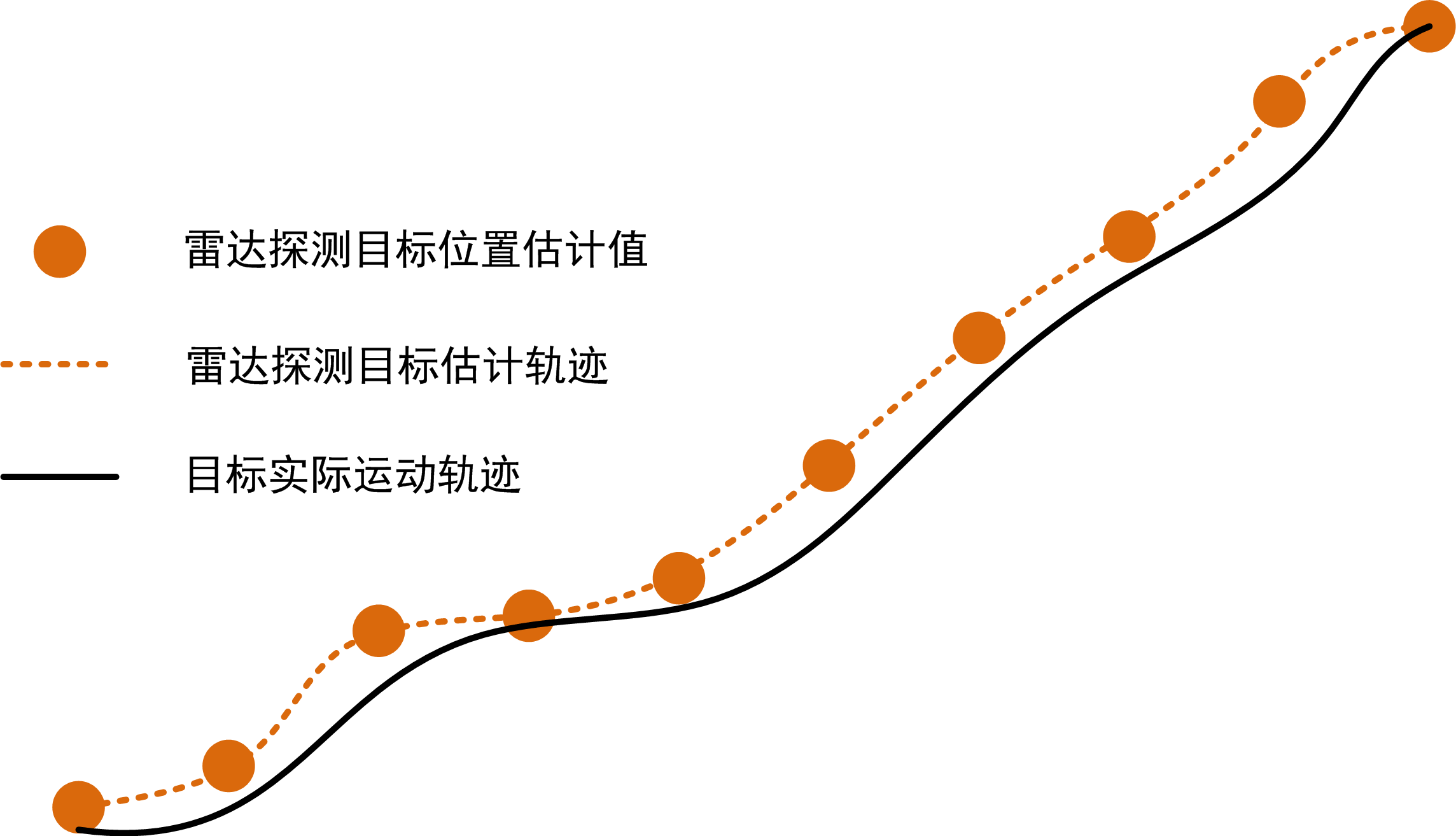
        真实的雷达测量均是在噪声存在的情形下去获取探测目标的状态信息（距离、角度、速度），其中距离和角度信息共同构成了当下时刻目标的位置信息，因此雷达探测的目标信息又可精炼成：位置、速度，两类。通常在雷达的实际显控中我们观测到的目标轨迹是一条相对平滑的曲线，如图1所示，然而该曲线却是雷达通过数据滤波处理在滤除部分噪声后获得的一系列合理估计点连接得到曲线，如图2所示。

图1 雷达探测目标时的雷达显控形成的目标运动轨迹

图2 雷达探测目标时实际观测值形成的目标运动轨迹

        那么滤波的基本原理是什么呢？为什么滤波后我们的运动曲线就变得光滑了呢？
我们已经知道雷达探测得到的位置观测值$\tilde{z}\left[n\right]$和速度观测值$\tilde{v}\left[n\right]$都是在噪声环境下观测得到的，若假设为加性高斯噪声即：
$$\tilde{z}\left[n\right]=z\left[n\right]+w_z\left[n\right]（1）$$
$$\tilde{v}\left[n\right]=v\left[n\right]+w_v\left[n\right]（2）$$
其中，$z\left[n\right]$、$v\left[n\right]$是目标位置和速度的客观真实值，$w_z\left[n\right]$、$w_v\left[n\right]$是目标位置和速度的观测噪声。根据贝叶斯估计的基本原理可知，若可以从观测值之外的其他来源获取客观真实值的部分信息，那么就可以讲这部分当作一种修正信息对观测值进行修正，从而得到更接近客观真实值的估计值$\hat{z}\left[n\right]$、$\hat{v}\left[n\right]$。
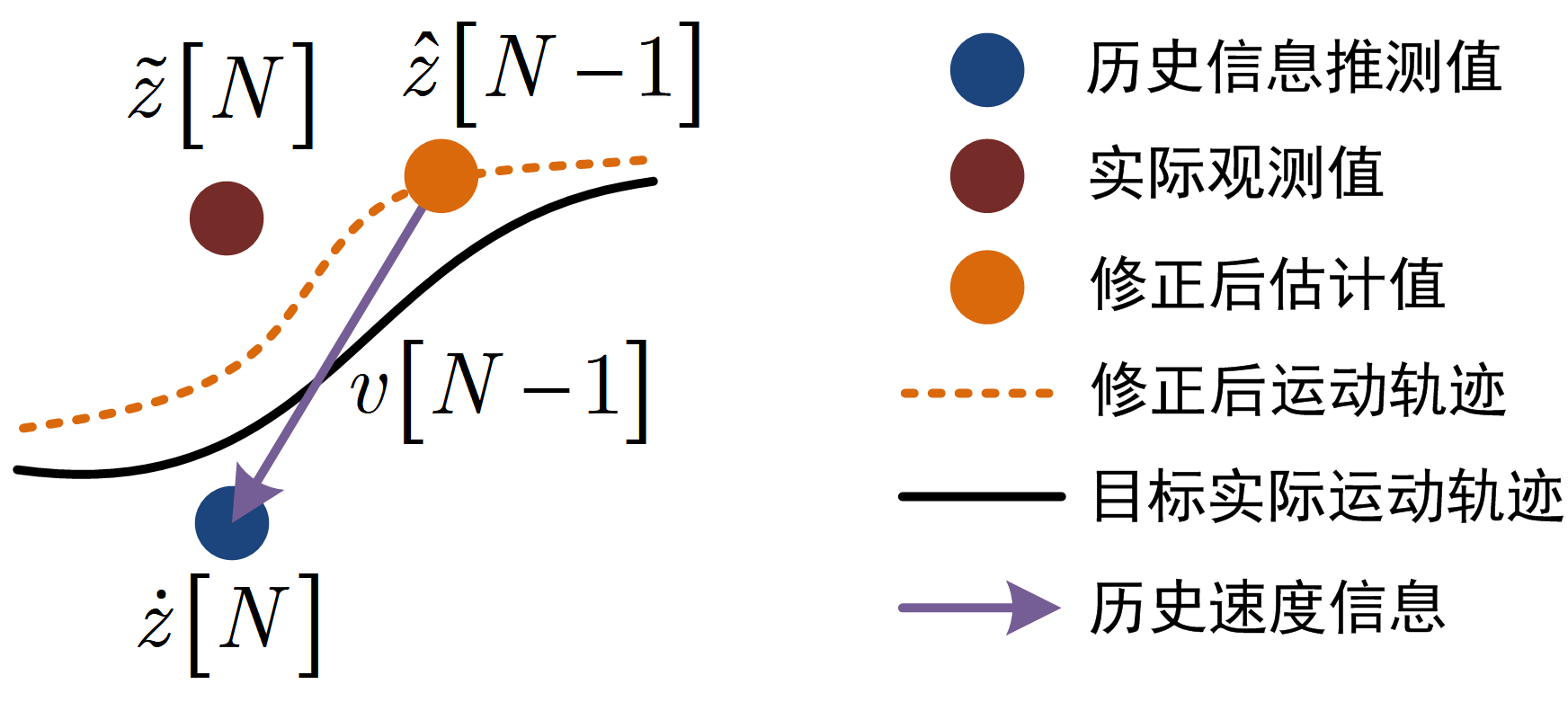
这篇内容主要理解位置信息的修正。在雷达探测场景中，这种修正信息可从历史信息中得到。在雷达探测中，由于我们是对宏观世界的物体进行探测，那么目标的状态肯定在时间前后上具有关联性。具体来讲，目标在当下$t_N$时刻的位置$z\left[N\right]$肯定可以通过$t_{N-1}$时刻的位置$z\left[N-1\right]$和$t_{N-1}$时刻的速度$v\left[N-1\right]$推测得到，如：
$$z\left[N\right]=z\left[N-1\right]+v\left[N-1\right]\cdot （匀速运动）（3）T$$
$$z\left[N\right]=z\left[N-1\right]+v\left[N-1\right]\cdot T+\frac{1}{2}a{T}^2（匀加速运动）（4）$$
其中$T$是时间采样间隔$T=t_N-t_{N-1}$，$a$是匀加速运动的加速度。即当目标是匀速、匀加速运动或其他速度变化规律已知的变加速运动时，目标当下时刻的位置$z\left[N\right]$可以由前一时刻的位置$z\left[N-1\right]$、速度$v\left[N-1\right]$直接计算得到的。实际情况中目标的这种速度变化规律雷达是不知道的，那么目标当下时刻的位置$z\left[N\right]$无法通过前一时刻的位置$z\left[N-1\right]$、速度$v\left[N-1\right]$直接计算得到。但是，由于雷达观测的是目标宏观物体，因此我们可以有一个合理的基本假设：目标在任意间隔$T$的两次观测之间的速度变化是渐变的而非突变的。在这个假设之下我们可以认为当观测时间间隔$T$较短时，雷达按照前一时刻位置$\hat{z}\left[N-1\right]$、速度$\hat{v}\left[N-1\right]$推测得到的当下时刻位置$\dot{z}\left[N\right]=\hat{z}\left[N-1\right]+\hat{v}\left[N-1\right]\cdot T$总是在客观真实位置$z\left[N\right]$附近的。如图3所示。由此，雷达就获得了关于目标客观真实位置$z\left[N\right]$的两个相关值，一个是当下时刻的观测值$\tilde{z}\left[N\right]$、一个是由之前的历史信息得到的推测值$\dot{z}\left[N\right]$，两个相关值同时指向客观真实值$z\left[N\right]$，且来自不同的信息来源。那么我们就可以通过用推测值$\dot{z}\left[N\right]$修正观测值$\tilde{z}\left[N\right]$的方法来获得更加接近客观真实值$z\left[N\right]$的估计值$\hat{z}\left[N\right]$，如图4所示。综合考虑这个过程，由于我们估计得到的值$\hat{z}\left[N\right]$考虑了由之前历史信息得到的推测值$\dot{z}\left[N\right]$，因此得到的目标运动轨迹$\hat{z}\left[n\right]$总是随时间渐变的、平滑的，而非突变的。

图3 推测依据示意图

图4 修正过程示意图