INT301 Bio-computation 生物计算（神经网络）Pt.7 时间序列预测和Elman网络

1. 时间序列（Time Series）

时间序列是一系列按时间顺序排列的、可比较的观察值$y_t$，这些观察值是在等距的时间间隔内记录的。
$y_t$表示第$t$个周期的观察值，其中$t=1,2,\dots ,n$。

例如：

1. 股票价格（Stock prices）：股票价格随时间变化，可以形成时间序列数据。
   

2. 温度读数（Temperature readings）：温度数据通常在固定的时间间隔（如每小时）记录，形成时间序列。
   

3. 脑电图（Electroencephalography脑电图）：脑电图是一种通过在头皮上放置电极来记录大脑电活动的技术。这些电极可以检测到大脑神经元产生的微小电流变化，从而生成脑电波的图形记录。

1.1 时间序列模型（Time Series Models）

时间序列建模是指使用统计方法和数学模型来分析和预测按时间顺序排列的数据点。这种建模可以帮助我们理解数据随时间变化的模式和趋势。
时间序列中连续时间点的值通常存在相关性。这种相关性是时间序列分析和预测的基础。如果时间序列中的值是完全随机的，那么预测就变得不可能。
时间序列的统计特性（如均值、方差等）在时间上是稳定的。这是许多时间序列模型的基本假设之一。
宽平稳（Wide-Sense Stationary，WSS）是平稳性的一种较弱形式，它要求时间序列满足以下两个条件：

1. 均值和自协方差不随时间变化。
2. 方差对所有时间都是有限的。

在统计学和机器学习中，时间序列通常被描述为一系列随时间变化的向量（或标量）。
这些向量或标量表示在不同时间点$t$上的观测值，例如{x(t0),x(t1),⋯,x(ti−1),x(ti),x(ti+1),⋯}\{x(t_0), x(t_1), \cdots, x(t_{i-1}), x(t_i), x(t_{i+1}), \cdots \}{x(t0​),x(t1​),⋯,x(ti−1​),x(ti​),x(ti+1​),⋯}

时间序列是某个过程 P 的输出，这个过程具有未知的动态特性（Unknown dynamics）。

我们的目标是通过分析观测到的时间序列数据来理解和预测这个过程的动态特性。

1.1.1 连续信号采样

连续信号$x(t)$是指在时间上连续变化的信号。例如，声音波形、温度变化等都可以视为连续信号。
为了将这些连续信号用于时间序列分析，需要在离散的时间点对其进行采样，从而得到一系列离散的观测值。
均匀采样（Uniform Sampling）是指以固定的时间间隔$\Delta t$对连续信号进行采样。
通过均匀采样得到的离散时间序列表示为{x[t]}\{x[t]\}{x[t]}。
因此这个序列表示为：{x[t]}={x(0),x(Δt),x(2Δt),x(3Δt),⋯}\{x[t]\}=\{x(0),x(Δt),x(2Δt),x(3Δt),⋯\}{x[t]}={x(0),x(Δt),x(2Δt),x(3Δt),⋯}

1.1.2 预测未来的问题

从时间点$t$向前延伸，我们有一个时间序列{x[t],x[t−1],⋯}\{x[t],x[t−1],⋯\}{x[t],x[t−1],⋯}。我们的目标是估计在未来某个时间点$t+s$的值$x$。
预测公式表示为：$\hat{x}[t+s]=f(x[t],x[t-1],\cdots )$
$s$被称为预测范围（horizon of prediction）。
在开始时，我们预测未来一个时间点，即$s=1$。
这是一个函数逼近问题（function approximation problem），我们需要找到一个合适的函数$f$来逼近真实的未来值。
我们的解决步骤如下：

1. 首先，我们需要假设一个生成模型，这个模型能够生成时间序列数据。
2. 对于过去的每一个点$x[t_i]$，使用$t_i$之前的数据作为输入，$t_i$之后的数据作为期望输出，来训练生成模型。
3. 使用训练好的模型，根据$(x[t],x[t-1],\cdots )$来预测$\hat{x}[t+s]$。

时间序列预测是一种统计方法，用于根据历史数据预测未来的趋势和行为。它在许多领域都有广泛的应用。
例如：

1. 金融领域：例如股票价格、汇率等。通过对历史金融数据的分析，可以预测未来的市场走势，从而做出投资决策。
2. 物理观测：例如天气变化、河流流量等。通过对历史观测数据的分析，可以预测未来的天气情况或河流水位，从而进行相应的规划和管理。

时间序列预测的重要性如下：

1. 预防不良事件：
   通过预测事件的发生，识别事件前的特定情况，并采取纠正措施，可以避免事件的发生。
   例如，在医疗领域，通过分析病人的历史健康数据，可以预测某些疾病的发生，从而提前采取预防措施。
2. 减轻不可避免事件的影响：
   对于一些不可避免的不良事件，通过预测可以提前采取措施，减轻其影响。
   例如，在自然灾害领域，通过预测地震、洪水等灾害的发生，可以提前疏散人员，减少损失。
3. 从预测中获利：
   在金融市场中，通过预测股票价格、汇率等，可以进行投资决策，从而获得收益。
   例如，通过对历史金融数据的分析，可以预测未来的市场走势，从而进行买卖操作，获得投资回报。

时间序列预测有以下难点：

• 数据量有限（Limited quantity of data）：
  可用的时间序列数据可能数量有限，这限制了模型训练的充分性和预测的准确性。
  时间序列数据可能太短，以至于无法有效地分割成训练集和测试集，这会影响模型的泛化能力。
• 噪声（Noise）：
  数据中可能存在错误数据点或噪声，这些会干扰模型的学习和预测。
• 非平稳性（Non-stationarity）：
  时间序列的统计特性（如均值、方差）可能随时间变化，这种非平稳性使得预测变得更加复杂。
• 预测方法的选择（Forecasting method selection）：
  存在多种预测方法，如统计方法和人工智能方法，选择合适的方法对于提高预测性能至关重要。

神经网络，尤其是前馈神经网络，已被广泛用于时间序列预测。这些网络通常使用滑动窗口方法处理输入序列。滑动窗口是一种技术，它在输入序列上移动，每次提取一个固定长度的子序列作为输入向量。
神经网络将时间序列$X_1,\dots ,X_n$视为多个从输入向量到输出值的映射。这意味着网络学习如何根据输入的一系列值（如过去的观测值）来预测下一个值。

1.1.2.1 使用人工神经网络（ANN）进行时间序列预测

我们用以下方式使用人工神经网络（ANN）进行时间序列预测：

1. 输入窗口的数据点映射：
   将时间序列中相邻的一系列数据点（输入窗口$X_{t-s},X_{t-s+1},\dots ,X_t$）映射到区间$[0,1]$，并用作输入层的激活值。
   这个步骤是为了将原始数据标准化或归一化，使其适合神经网络处理。
2. 输入窗口的大小与神经网络的输入单元数：
   输入窗口的大小$s$对应于神经网络输入层的单元数。
   这意味着如果输入窗口包含$s$个数据点，那么输入层将有$s$个神经元。
3. 前向传播和误差计算：
   在前向传播过程中，激活值通过隐藏层传播到输出单元。
   用于反向传播训练的误差是通过比较输出单元的值与时间序列在时间$t+1$的实际值来计算的。
   这个过程涉及到损失函数，它衡量了预测值与实际值之间的差异。
4. 多层感知器网络的训练：
   使用反向传播学习算法训练多层感知器（MLP）网络通常需要多次呈现所有输入集的表示（称为一个epoch）。
   这意味着在训练过程中，整个训练数据集需要被多次遍历，以便网络能够学习到数据中的模式和关系。

下图展示了使用人工神经网络（ANN）进行时间序列预测的结构示意图。

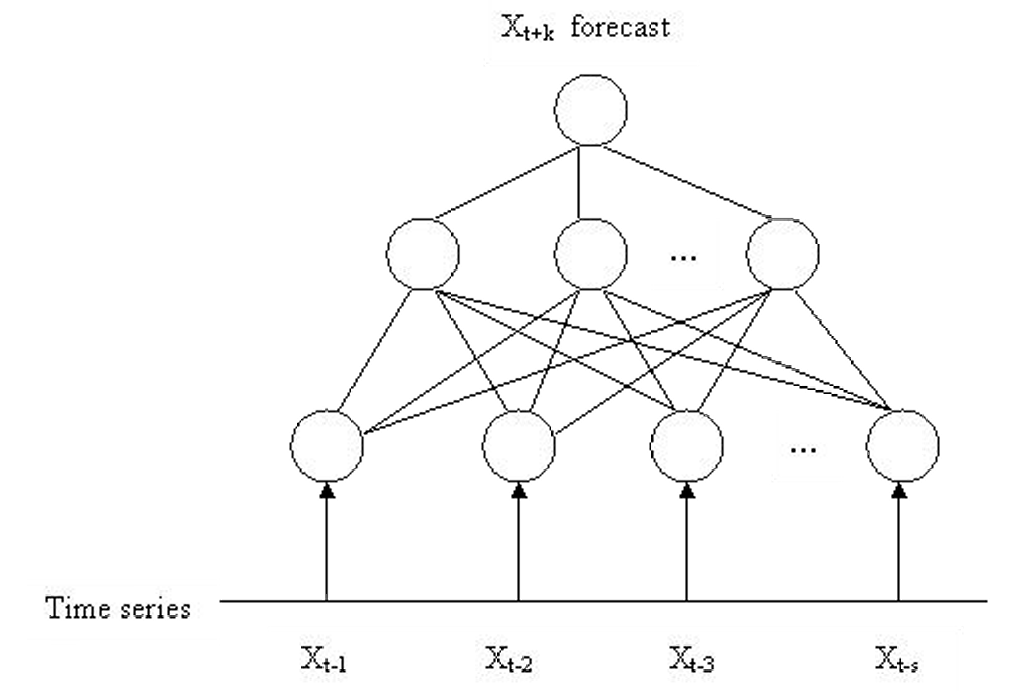
我们这里稍微复习一下前面所学的前馈神经网络（Feed Forward Neural Network，FNN）。前馈神经网络是一种常见的神经网络结构，其中信息从输入层流向输出层，不形成闭环。
通过训练（例如使用反向传播算法），带有隐藏节点的前馈神经网络会发展出内部表示，这些表示对输入信号进行重新编码。
这种重新编码使得网络能够以一种方式处理输入信号，从而产生正确的输出。

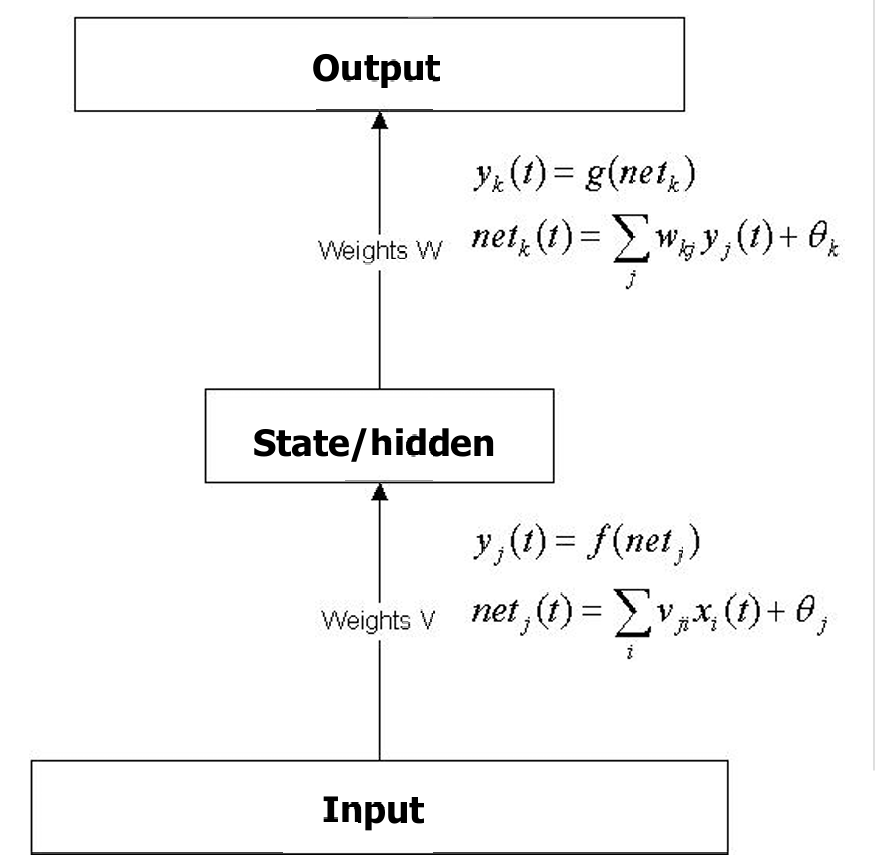
输入层接收输入信号，隐藏层处理这些信号，输出层生成最终的输出。
对于隐藏层的每个神经元$j$：
$y_j(t)=f(ne{t}_j)$
$ne{t}_j(t)={\sum }_i(v_{ji}{x}_i(t))+{\theta }_j$
其中，$y_j(t)$是神经元$j$在时间$t$的输出，$f$是激活函数，$ne{t}_j$是神经元$j$的净输入，$v_{ji}$是从输入层到隐藏层的权重，$x_i(t)$是输入信号，${\theta }_j$是神经元$j$的偏置项。
对于输出层的每个神经元$k$：
$y_k(t)=g(ne{t}_k)$
$ne{t}_k(t)={\sum }_j{w}_{kj}{y}_j(t)+{\theta }_k$
其中，$y_k(t)$是输出层神经元$k$在时间$t$的输出，$g$是激活函数，$ne{t}_k$是神经元$k$的净输入，$w_{kj}$是从隐藏层到输出层的权重，$y_j(t)$是隐藏层神经元$j$的输出，${\theta }_k$是神经元$k$的偏置项。

1.2 动态网络（dynamic networks）

有时，我们希望模型对一段时间前呈现的输入保持敏感。
这意味着我们的需求不能仅通过一个函数（无论它多么复杂）来满足，而是需要一个能够维护状态或记忆的模型，这些状态或记忆可以跨越多个输入呈现。
序列输入（sequential input）：例如语言理解、机器人探索等。在这些应用中，理解当前输入通常需要考虑之前的输入信息。
序列输出（sequential output）：例如语音生成、路线规划等。在这些应用中，生成当前输出通常需要考虑之前的输出信息。
输入和输出的组合：有些应用可能同时需要处理序列输入和序列输出，例如机器翻译，其中输入是一段文本序列，输出是另一段文本序列。

因此动态网络的好处如下：

1. 记忆和状态维护：动态网络能够维护一个内部状态，这个状态可以随时间更新，从而允许网络“记住”过去的信息。
2. 处理序列数据：动态网络特别适合处理序列数据，因为它们可以利用过去的信息来影响当前的决策或输出。
3. 复杂模式识别：在处理复杂的序列模式时，动态网络可以更好地捕捉长期依赖关系，这是静态模型难以做到的。

1.2.1 序列学习（Sequence Learning）

多层感知器（MLP）和径向基函数（RBF）网络是静态网络（Static Networks）的例子。
静态网络学习从单个输入信号到单个输出响应的映射。
它们可以处理任意数量的输入输出对，但每个输入输出对都是独立的。

动态网络（Dynamic Networks）学习从单个输入信号到一系列响应信号的映射。
它们可以处理任意数量的输入序列对（输入信号和对应的输出序列）。
动态网络的输入信号通常是序列中的一个元素，然后网络生成序列的其余部分作为响应。
例如：

1. 文本生成：假设我们有一个文本序列：“我今天很开心”。
   如果网络的输入是“我今”，网络的任务可能是生成序列的下一个单词“天”。
   网络通过学习语言模式和上下文关系来预测下一个合适的单词。
2. 时间序列预测：假设我们有一个股票价格的时间序列。
   如果网络的输入是最近几天的股票价格，网络的任务可能是预测接下来几天的价格。
   网络通过分析历史价格数据和可能的趋势来预测未来的价格。

为了学习序列，网络需要包含某种形式的记忆（短期记忆）。
这是因为序列数据具有时间依赖性，网络需要记住过去的信息来预测未来的值。

1.2.1.1 记忆效应（Memory Effect）

记忆效应（Memory Effect）是指系统能够记住过去发生的事件，并利用这些信息来影响当前或未来的行为。具体来说是网络或模型能够利用过去的输入数据来影响当前的输出或预测。
序列学习中的记忆效应分为两种主要方式：隐式（Implicit）和显式（Explicit）。

1. 隐式（Implicit）：
   隐式记忆效应是通过将时间延迟的信号作为输入提供给静态网络，或者通过循环连接（recurrent connections）来实现的。
   在这种方法中，我们假设收集（输入信号，输出序列）示例的环境是静止的（stationary）。这意味着环境的统计特性不随时间变化，例如，时间序列数据的均值和方差在时间上保持恒定。
2. 显式（Explicit）：
   显式记忆效应是通过明确设计网络结构来实现的，例如使用时间反向传播方法（Temporal Backpropagation Method）。
   显式形式允许环境是非静止的（non-stationary），即网络能够跟踪信号结构的变化。这意味着网络可以适应环境的变化，例如，时间序列数据的统计特性可能随时间变化。

1.2.1.1.1 时间延迟网络（Time Delayed Networks）

时间延迟网络是一种特殊的神经网络结构，它通过引入时间延迟的输入来处理序列数据。
这种网络结构使得网络能够利用过去的输入信息来影响当前的输出。
信号可以被外部缓冲（buffered externally），并在额外的输入节点（input banks）上呈现。这样网络可以接收一系列时间延迟的输入信号，这些信号是在过去不同时间点上收集的。
时间延迟网络展示了一种隐式的序列学习方法，它将静态网络（如多层感知器MLP或径向基函数RBF）与记忆结构结合起来。
通过这种方式，网络能够在没有显式记忆单元的情况下，利用过去的输入信息来处理序列数据。

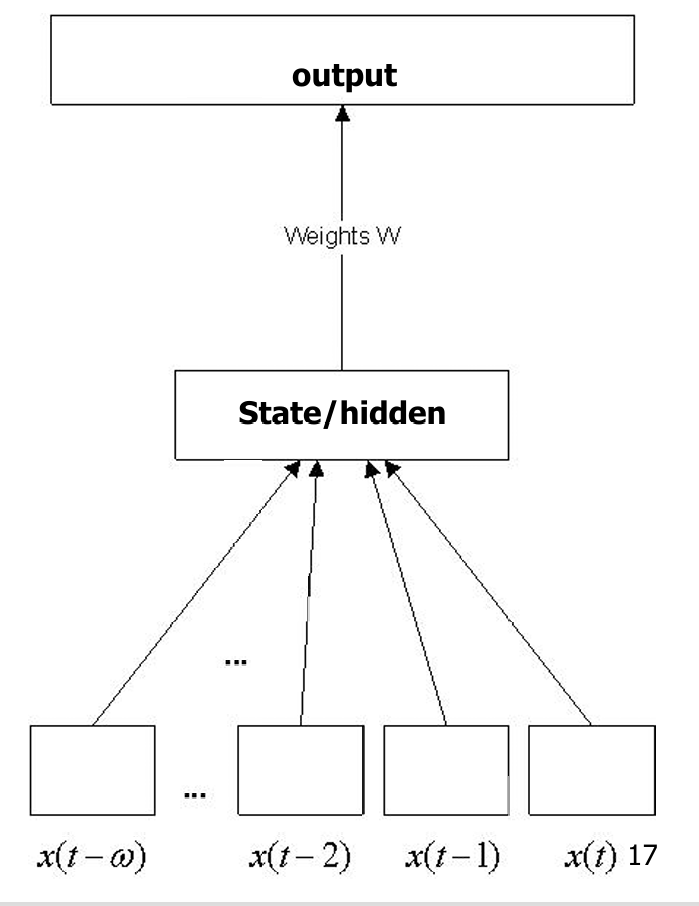
输入层接收一系列时间延迟的信号，如$x(t-\omega ),x(t-2),x(t-1),x(t)$。
这些输入信号被连接到隐藏层（State/hidden），隐藏层通过权重$W$将信息传递到输出层。
输出层生成最终的输出。

1.2.1.1.2 动态神经网络（Dynamical Neural Networks）

动态神经网络能够根据输入数据和内部状态动态地调整其行为，这使得它们非常适合处理具有时间依赖性的任务。我们重点介绍循环网络。
循环网络可以显式地处理按顺序呈现的输入，这在现实问题中几乎总是如此。
循环网络与前馈网络（Feed Forward Networks）在本质上是不同的。循环网络不仅处理输入数据，还处理网络的状态。这种状态可以看作是网络的内部记忆，它允许网络记住过去的输入信息，并利用这些信息来影响当前和未来的输出。
网络的回响（reverberate）和持续活动的能力可以作为工作记忆（working memory）。这意味着网络能够在一段时间内保持信息，即使在没有新的输入的情况下也能继续处理信息。
具有这种能力的网络被称为动态神经网络。

下图将前馈神经网络（Feed-Forward Neural Networks）和循环神经网络（Recurrent Neural Networks，RNN）进行了对比。

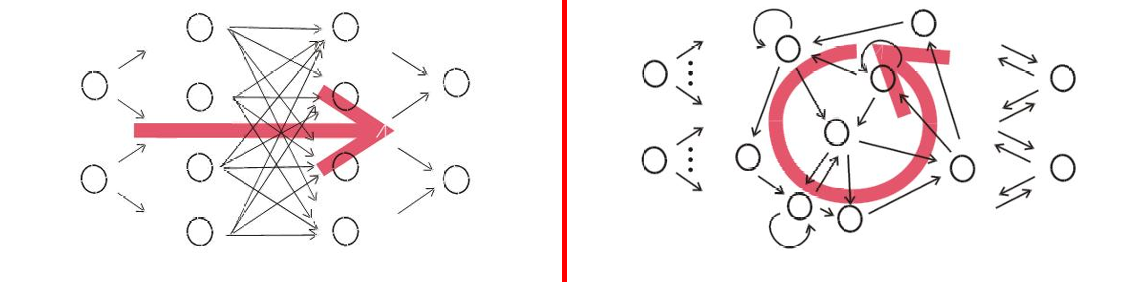
左侧（前馈神经网络）：
连接方向：连接仅从左到右，没有连接循环（即没有反馈连接）。
激活传播：激活值从输入层通过隐藏层向前传播到输出层，没有反馈回路。
记忆能力：前馈网络没有记忆能力，因为它们不存储过去的信息。

右侧（循环神经网络）：
连接循环：至少存在一个连接循环，即网络中存在反馈连接，使得信息可以在网络中循环流动。
激活回响：激活可以“回响”（reverberate），即使在没有新输入的情况下也能持续存在。这意味着网络可以维持内部状态。
记忆系统：循环网络具有记忆能力，可以存储和利用过去的信息。
动态系统：从数学角度来看，RNN实现了动态系统。这意味着它们的行为和输出可以随时间变化，并且对初始条件敏感。

我们再总结一下显式和隐式记忆效应。
显式记忆效应涉及到对神经网络结构的直接修改，以引入一种机制来明确地存储和利用过去的信息。
隐式记忆效应不涉及对网络结构的直接修改，而是通过控制输入或利用网络的学习能力来间接利用过去的信息。

2. Elman网络

Elman网络是一种循环神经网络，这意味着它具有循环连接，可以将网络的输出反馈到输入，从而允许信息在网络中循环流动。
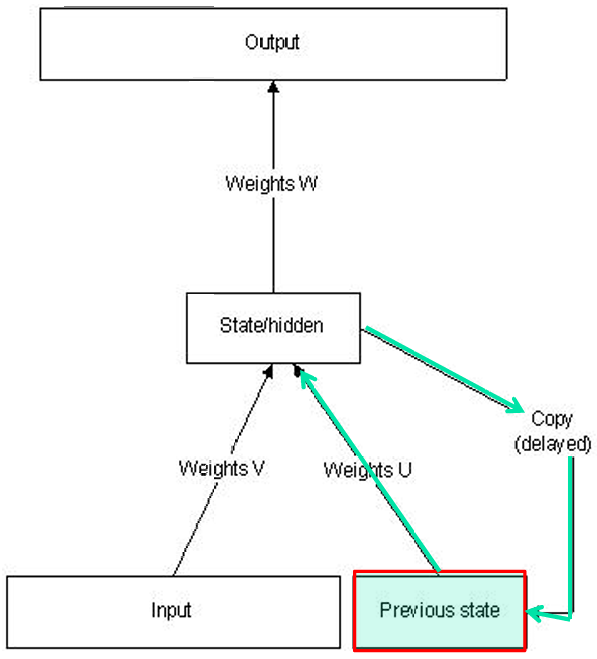
Elman网络除了传统的三层：输入层、隐藏层和输出层。此外，它还有一个额外的层，称为上下文层（context layer）或记忆层，用于存储隐藏层的输出。
Elman网络具有强大的预测能力，这主要得益于其循环连接和上下文层。通过这些结构，网络可以利用过去的信息来预测未来的输出。

2.1 Elman网络的结构

Elman网络包含以下几个部分：

1. 输入层（Input）：
   输入层接收外部输入信号$x$。
2. 隐藏层（State/Hidden）：
   隐藏层处理输入信号，并生成内部状态$z$。
   隐藏层的输出不仅用于生成最终的输出，还被复制到上下文层（Context Layer）。
3. 上下文层（Context Layer）：
   上下文层存储隐藏层的输出，作为网络的短期记忆。
   上下文层的输出被反馈到隐藏层，形成循环连接。
4. 输出层（Output）：
   输出层生成最终的输出$y$，基于隐藏层的当前状态和上下文层的状态。

$W$：从隐藏层到输出层的权重。
$V$：从输入层到隐藏层的权重。
$U$：从上下文层到隐藏层的权重，用于形成循环连接。

状态更新：$z^t=F_v(z^{t-1},x)$，其中：
$z^t$是时间$t$时刻的状态。
$z^{t-1}$是时间$t-1$时刻的状态。
$x$是当前的输入。
$F_v$是状态更新函数，通常是一个非线性激活函数。
输出生成：$y=F_w(z)$，其中：
$y$是网络的输出。
$F_w$是输出生成函数，通常也是一个非线性激活函数。

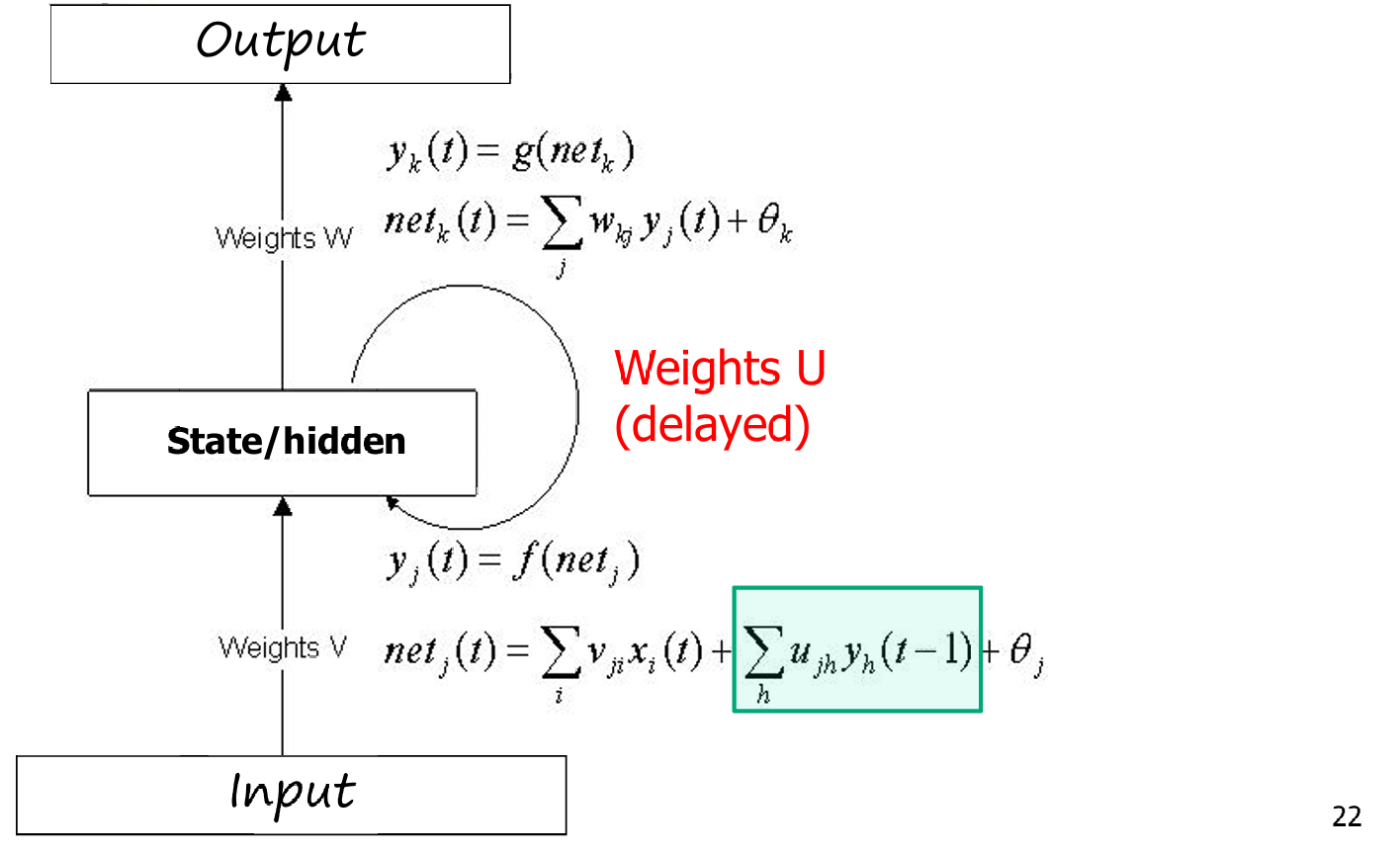
隐藏层的净输入和输出：
$ne{t}_j(t)={\sum }_i{v}_{ji}{x}_i(t)+{\sum }_h{u}_{jh}{y}_h(t-1)+{\theta }_j$
$y_j(t)=f(ne{t}_j)$
其中：
$ne{t}_j(t)$是隐藏层第$j$个神经元在时间$t$的净输入。
$v_{ji}$是从输入层到隐藏层的权重。
$u_{jh}$是从上下文层（隐藏层的前一状态）到隐藏层的权重（延迟的反馈）。
${\theta }_j$是隐藏层第$j$个神经元的偏置。
$f$是激活函数。

输出层的净输入和输出：
$ne{t}_k(t)={\sum }_j{w}_{kj}{y}_j(t)+{\theta }_k$
$y_k(t)=g(ne{t}_k)$
其中：
$ne{t}_k(t)$是输出层第$k$个神经元在时间$t$的净输入。
$w_{kj}$是从隐藏层到输出层的权重。
${\theta }_k$是输出层第$k$个神经元的偏置。
$g$是激活函数。

Elman网络中使用的方程与前馈神经网络（Feed Forward Neural Networks）中的方程在形式上是相同的。这包括如何计算神经元的净输入（net input）以及如何根据净输入通过激活函数生成输出。
Elman网络与前馈网络的主要区别在于引入了另一组权重（通常表示为 U），这组权重负责将隐藏层（hidden nodes）的激活值反馈到隐藏层自身。这种连接方式允许网络在处理序列数据时能够维持一个内部状态，或称为“记忆”。

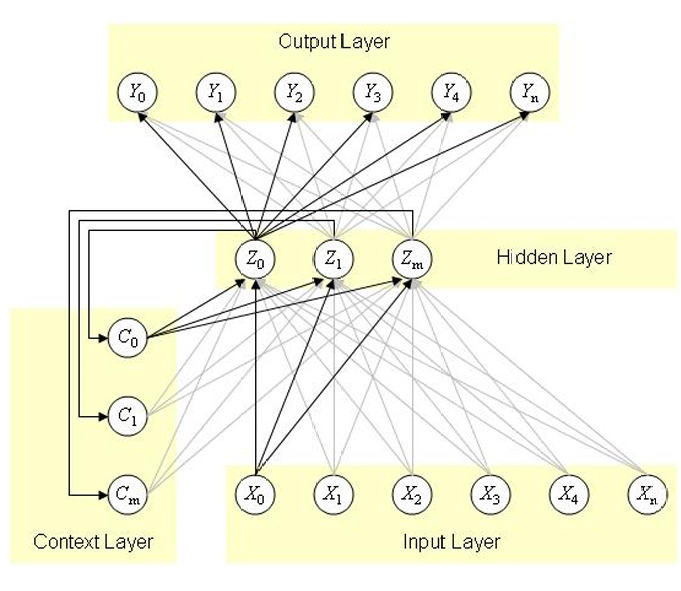
所以Elman网络的主要特点和区别确实在于隐藏层与上下文层之间的交互方式：
隐藏层（Hidden Layer）：
隐藏层负责形成内部表示，处理输入层传来的数据，并生成内部状态。
隐藏层的输出不仅用于生成最终的输出，还被复制到上下文层。
上下文层（Context Layer）：
上下文层存储隐藏层的输出，作为网络的短期记忆。
上下文层的值被用作隐藏层所有神经元的额外输入信号，用于下一个时间步。
在Elman网络中，从隐藏层到上下文层的权重被设置为1并固定，以确保上下文神经元的值能够被精确复制。

总结一下：
隐藏层的激活值（即隐藏层神经元的输出）在每个时间步被复制并存储在上下文层中。上下文层可以被看作是隐藏层状态的“快照”，它记录了前一时间步隐藏层的信息。
在下一个时间步，上下文层中的值被用作额外的输入，反馈到隐藏层。这意味着隐藏层在处理当前输入时，不仅考虑当前的输入数据，还会考虑前一时间步的隐藏层状态（即上下文层提供的值）。

2.2 Elman网络的学习算法

Elman网络采用反向传播算法（Backpropagation，BP）来调整网络的权重。
Elman网络使用的误差函数：$E={\sum }_{k=1}^n[y(k)-d(k){]}^2$，其中：
$E$是总误差。
$y(k)$是网络在第$k$个时间步的实际输出。
$d(k)$ 是第$k$个时间步的期望输出（目标值）。
$n$是时间步的总数。