当前位置：首页 > news >正文

算法的初步认识

news 2025/11/11 12:36:27

什么是算法

算法（Algorithm）一词源于公元 9 世纪一位波斯数学家的名字，原意指计算步骤或规则，完全属于数学范畴。事实上，对算法的研究比这个词出现要早很多。

比如：求两个正整数 m、n（m>n）的最大公因数的欧几里得算法（辗转相除法）。

计算 m 除以 n 所得的余数 r；若 r=0，则 m 和 n 的最大公因数等于 n；若 r>0，则 m 和 n 的最大公因数等于 n 和用 n 除 m 的余数的最大公因数。

此算法在中国古代数学家秦九韶的《数学九章》中也有记载。求若干数的最小公倍数的孙子算法等也有类似。

算法是将问题的输入转化为输出的操作步骤的集合。

算法获得空前研究和广泛应用是出现了计算机后。在计算机科学中，“算法”一词有特殊的意义，特指用计算机求解某一问题的方法。所以，这里讨论的是用计算机语言描述的，能在计算机上执行的各种算法。

数学算法与计算机算法是有差异的。由于计算机本身是有限离散结构，决定了计算机所能处理的问题必须是确定有解的，而且能在有限步骤内得到解。有的问题可将求解过程写成算法，由计算机求解，有的问题则不能，如：求二次方程的复数根。一个问题能否由计算机求解，属于可计算性理论研究的范畴。

有的问题虽然可由计算机求解，但手工算法大不相同。

如：求定积分 $s=\int_{a}^{b}f(x)dx$ ，人工处理步骤如下：找出 f(x) 的原函数 F(x)；利用牛顿-莱布尼兹（Newton-Leibniz）公式：

$\int_{a}^{b}f(x)dx=F(b)-F(a)$

计算 s=F(b)-F(a)。

说明：牛顿-莱布尼兹公式也称为微积分基本公式，揭示了定积分和被积函数的原函数或者不定积分之间的关系。若 F(x) 是连续函数 f(x) 在区间 [a,b] 上的增量。

实例：量水问题

两只没有刻度的桶 A 和 B，其中 A 的容量为 7 升，B 为 5 升。问：如何能通过相互之间的倒腾，量出 6 升水来？

1. 重复下述步骤（2,3,4,5）两次
2.    将 A 装满；
3.    将 A 的水倒向 B（满为止）；
4.    倒空 B；
5.    将 A 中剩的水倒向 B；
6. 将 A 装满；
7. 将 A 的水倒向 B（满为止）

解答这个题目的方法：给出操作步骤，任何人按照这个步骤执行，都可以得到所要的结果。

算法：准确描述的 “操作步骤”

实例：求 π 问题

π 的定义：圆周长和直径的比，称为圆周率。

思路参考：圆面积=πr²（此处r=0.5）与正方形面积（此处为 1）之比近似等于圆中随机落点与在正方形中落点个数之比。

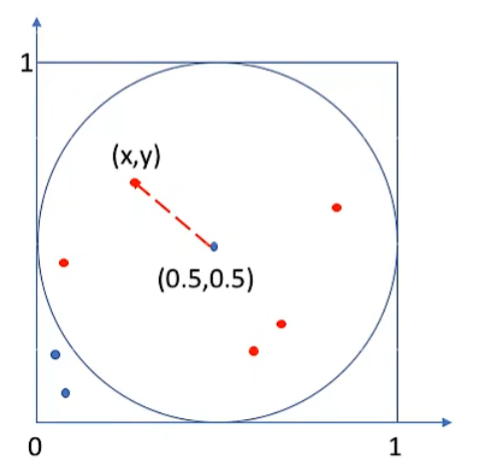
圆面积=πr²

πr²≈圆中落点数/正方形中落点数

π≈4•圆中落点数/正方形中落点数

假设有办法产生任意多在单位正方形中的随机点（x，y）。设总共产生 n 个点，用 in_circle 记录落在圆中的个数。

for i = 1 to n# 随机生成单位正方形中一个点（x，y）# 如果（x，y）与圆心（0.5,0.5）之间的距离<0.5# in_circle = in_circle + 1

算法结束时：4*in_circle/n 即为所求

描述的操作步骤，尽管不一定是精确的结果

什么是计算机算法——从特殊到一般的追求

计算机算法思路，首先考虑是否可能，其在在可能得情况下给出具体的操作步骤。

而计算机计算定积分采用数值积分法，得到的是一个近似解，因为用程序很难找到原函数。那么，作为计算机算法，应具备哪些基本特征呢？

算法特征

有穷性（Finiteness）

一个算法须在执行有限运算步骤后终止，每个步骤必须在有限时间内完成。实际应用中，算法的有穷性应该包括执行时间的合理性。

确定性（Definiteness）

算法的每个步骤必须有确定的含义，对每种可能出现的情况，算法都应给出确定的操作，不能有多义性。

如：计算分段函数

$f(x)=\left\{\begin{matrix} 1,x>100 & \\ 0,x<10 & \end{matrix}\right.$

算法描述：

输入变量 x
若 x 大于 100，则输出 1
若 x 小于 10，则输出 0

在异常情况下（输入 $10\leqslant x \leqslant 100$ ），算法的执行结果是不确定的。

有效性（Effectiveness）

算法中的每个步骤都是能实现的，算法的执行结果应达到预期目的，即正确、有效。如算法执行过程中出现 x/0、复数开方等操作将导致算法无法执行。

有 0 个或多个输入项

至少有一个输出项

算法和程序是有区别的。因为程序不一定要满足有穷性的要求，如操作系统除非死机，否则他永远再循环等待。另外，算法必须有输出，而程序可以没有输出。

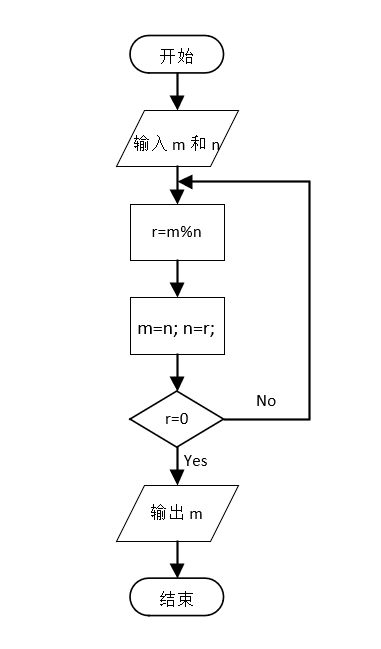
如：欧几里得算法，描述如下。

输入两个正整数 m、n（m>n），输出这两个数的最大公因数 gcd(m,n)。

Step1：输入两个正整数 m、n。

Step2：计算 m 除以 n，所得的余数赋给 r。

Step3：先将 n 的赋值给 m，再将 r 的值赋给 n。

Step4：若 r=0，则返回 m 的值作为结果，过程结束，否则进入 Step2。

对每个合法输入，该算法都会在有限的时间内输出一个满足要求的结果。计算最大公约数的欧几里得算法的正确性基于 gcd(m,n)=gcd(n,m,modn) 的正确性。该算法每座一次循环，第二个数字就会变得更小，最后算法会在第二个数字变为 0 时停止。

算法描述

如何描述一个算法呢？

算法描述的目的是让阅读者了解算法的工作流程和步骤，因此只要清楚表现算法的 5 个特性即可。常用的算法描述有三种方式：自然语言描述、流程图描述、伪代码描述。

自然语言描述

一般的日常文字叙述，如文字、英文、数字等，其特色在于，使用文字或语言说明操作步骤。欧几里得算法就是自然语言描述。

流程图描述

流程图是用一组集合图形表示各种类型的操作，在图形上用扼要的文字和符号表示具体的操作，并用带有箭头的流线表示操作的先后次序。

流程图的基本符号及其意义
图形符号	名称	含义
	起止/结束框	表示算法的开始或结束
	输入/输出框	表示输入/输出操作
	处理框	表示处理或运算功能
	判断框	根据是否满足给定的条件决定执行两条路径中的某一路径
	流线	表示程序执行的路径，箭头代表方向
	连接符	表示算法流向的出口连接点或入口连接点，同一对出口与入口的连接符内，必须标以相同的数字或字母

伪代码描述

伪代码描述是一种介于自然语言和计算机语言之间的描述形式。其比自然语言简洁，又比计算机语言灵活，没有严格的语法，但很容易转换成计算机语言程序。常用的有类 Pascal 语言、SPARKS、类 C 语言等。

下面是用伪代码写成的欧几里得算法。

euclid(m,n)
dor := m mod n;m := n;n := r;
while r≠0;
return m;

算法结构

不管算法多复杂，都是由顺序结构、选择结构、循环结构这三块“积木”通过组合和嵌套表达出来的，这样表达的算法结构清晰，易于验证和纠错。遵循这种方法的程序设计，就是结构化程序设计。正确理解和识别三种基本结构是描述算法的关键所在。

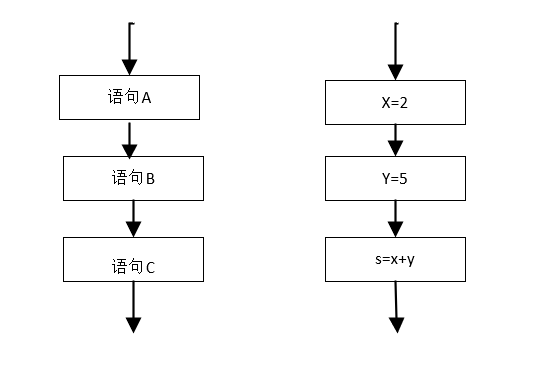
顺序结构

顺序结构是最简单的算法结构，语句是按从上到下的顺序执行的。语句的执行顺序为 A→B→C。

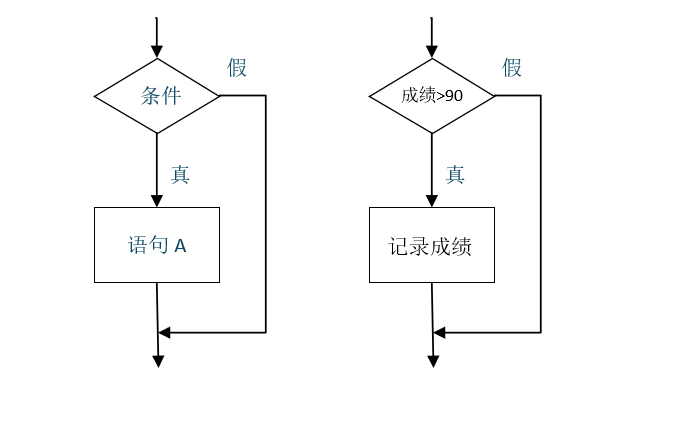
选择（分支）结构

选择（分支）结构的伪代码描述为：

if 条件 then A
else B

这种结构对给定条件进行判断，条件为真时执行语句 A，条件为假时执行语句 B。

其流程图基本形状有两种。

当条件真时执行语句 A，否则执行语句 B。

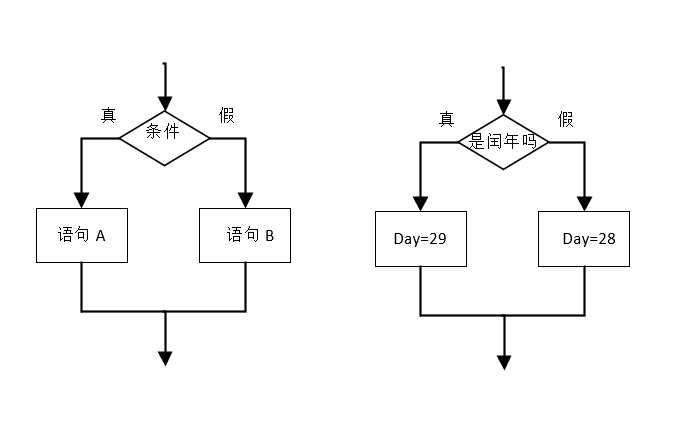
当条件为真时执行语句 A，否则什么也不做。

循环结构

重复执行同一组操作的结构称为循环结构，即从某处开始，按照一定条件反复执行某一处理步骤。反复执行的处理步骤称为循环体。循环结构有两种基本形态：当型循环和直到型循环。

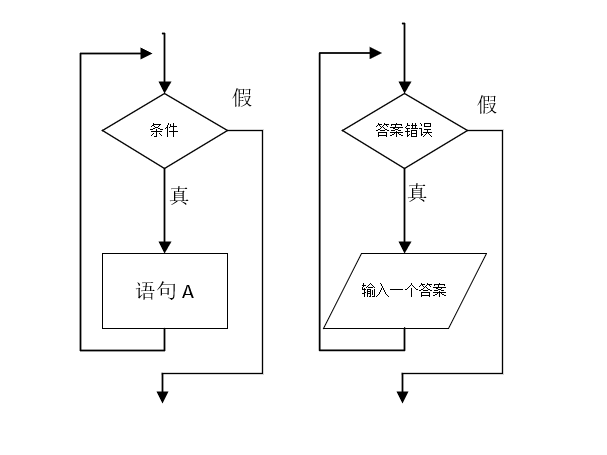
当型循环结构，执行序列是：当条件为真时，反复执行 A，一旦条件为假，跳出循环，执行循环体后的语句。

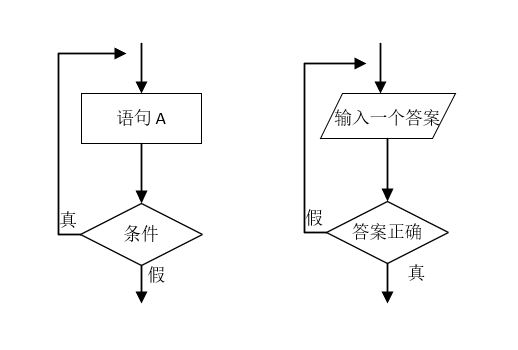
直到型循环，执行序列是：首先执行 A，在判断条件，条件为真时，循环执行 A，一旦条件为假，结束循环，执行循环后的下一条语句。

在两种结构流程中，语句 A 称为循环体，条件被称为循环控制条件。注意：在循环体中，必然会对条件的判断值进行修改，使经过有限次循环后，循环一定能结束。

当型循环中，循环可能一次都不执行，而直到型循环至少执行一次循环体。

三种基本结构的共同特点是：

（1）只有一个入口和一个出口。

（2）结构内的每一部分都有机会执行到，也就是说，每个框架都应当有一条从入口到出口的路径通过。

（3）结构内不存在死循环。

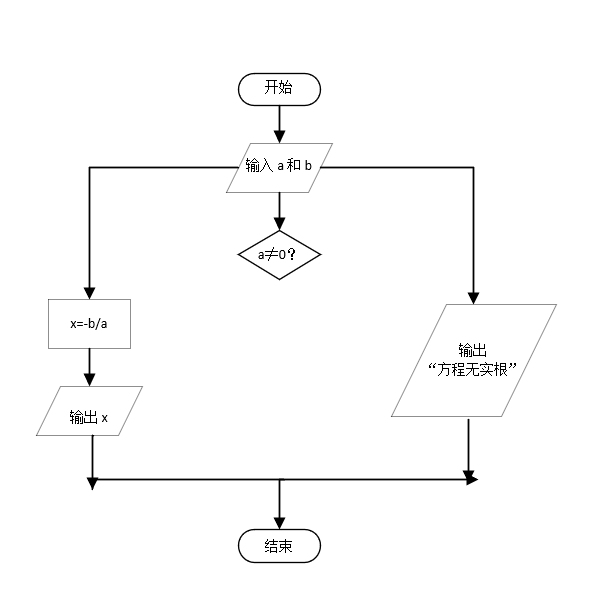
给出求方程 ax+b=0（a 和 b 为实数）实根的一个算法，并画出流程图。

此方程的根 a 和 b 的取值有关。算法如下：

1 输入 a 和 b。
2 如果 a≠0，x=-b/a，那么执行 3 ；否则，执行 4.
3 输出 x；结束。
4 输出“方程无实根”；结束。

流程图

算法设计方法

如何才能设计一个好的算法呢？

这在很大程度上依赖设计者个人的学识水平，因此有人说算法设计更像一门艺术，而不是一门技术。

但是算法设计还是有一些可以遵循的策略或方法的。常用的几种算法设计方法：

递归法

一个直接或间接地调用自身的算法称为递归算法。

在使用递归策略时，必须有一个明确的递归结束条件，称为递归出口。通常情况下，递归调用都受条件控制，而且被调用过程中会对调用条件进行修改，最终满足结束递归调用的条件，并逐级返回。

所以，递归算法一般包含三个基本部分：

当前问题 $Q_{n}$ ；

从较简单的问题 $Q_{n-1}$ 到 $Q_{n}$ 的操作；

已解决的基础问题 $Q_{0}$ 。

实例：用递归策略求 n！。

因为 n！=1+2+3+┅+n=n×(n-1)!，设f(n)=n!，那么

f(n-1)=(n-1)!

f(n)=f(n-1)×n

实例：汉诺塔问题的递归算法。将 n 个盘子从 A 塔座移动到 C 塔座可以分解以下三个步骤。

1 将 A 塔座上 n-1 个盘子借助 C 塔座先移动到 B 塔座上。

2 把 A 塔座上剩下的一个盘子移动到 C 塔座上。

3 将 n-1 个盘子从 B 塔座借助 A 塔座移动到 C 塔座上。

上面的 1 和 3 都是把 n-1 个盘子从一个塔座移到另一个塔座上，采取的办法一样，只是塔座的名字不同而已。为此，可以把上面三个步骤分成两类操作：

①将 n-1 个盘子从一个塔座移动到另一个塔座上（n>1）。

②将 1 个盘子从一个塔座移到另一个塔座山。

这就是递归，递归出口的条件是 n=1。

分治法

将规模为 n 的问题分解为 k 个规模较小的子问题，而这些子问题相互独立且可分别求解，再将 k 个子问题的解合并成原问题的解。若子问题的规模仍很大，则反复分解直到问题小到可直接求解为止。在分治法中，子问题的解法通常和原问题相同，从而导致递归过程。

实例：将 n 个整数递增排序。

采用合并排序的算法策略：若 n 为 1，算法终止；否则，将 n 个待排元素分割成 k（k=2）个大致相等的子集合 A 和 B，对每个子集合分别进行递增排序，再将排好序的子集归并为一个集合。

实例：

初始序列：[8] [4] [5] [6] [2] [1] [7] [3]一次归并：[4 8]    [5 6]    [1 2]    [3 7]二次归并：[4 5 6 8]         [1 2 3 7]三次归并：[1 2 3 4 5 6 7 8]

归并过程从两个序列的头部开始。如：归并 [4,5,6,8] 和 [1,2,3,7] 时：4 和 1 比较，1 被移入结果序列；4 和 2 比较，2 被移入结果序列；4 和 3 比较，3 被移入结果序列；4 和 7 比较，4 被移入结果序列；5 和 7 比较 ……

贪心法

问题的求解过程被划为多步选择，每次都是在条件允许范围内找一个当前最好的选择，由感步的选择构成问题的最终解。贪心法以当前情况为基础进行最优选择，而不考虑各种可能的体情况，一般可以快速得到问题的解，但并不总能找到最优解，

实例设计一个算法使找回的零钱的硬币数最少

算法思路：划分为多步选择，每次选取一个硬币，策略是先尽量用大面值的币种，这就是贪心策略。所以，算法是从最大面值的币种开始取硬币，当余额不足硬币面值时，取下一种较小面值的币种。

如面值分别为1、5 和 10 单位的硬币，而希望找回总额为 15 单位的硬币。按贪心算法，应找 1 个 10 单位面值的硬币和 1 个 5 单位面值的硬币，共找回 2 个硬币。这是最优解。但如果面值分别为1、5 和 11 单位的硬币，贪心策略的解是 1 个 11 单位面值的硬币和 4 个 1 单位面值的硬币，共找回 5 个硬币，而最优解是 3 个 5 单位面值的硬币。

回溯法

回溯法，也称为“万能算法”，求解过程相当于在所有可能解构成的解空间树中搜索满足约束条件的解。

实例：0-1 背包问题。设有 n 个物体和一个背包，物体 i 的重量为 $w_{i}$ ，价值为 $p_{i}$ ，背句的载荷为 M。若将物体 i（1 ≤ i ≤ n）装入背包，则有价值为 $p_{i}$ 。目标是找到一种方案，使放人背包的物体总价值最高。

n=3

w=( $w_{1},w_{2},w_{3}$ )=(20,15,15)

算法思路（通过实例说明）：设 p=( $p_{1},p_{2},p_{3}$ )=(40,25,25)

M = 30

问题的解为x=( $x_{1},x_{2},x_{3}$ )，那么

问题所有可能得解为 (0,0,0)，(0,0,1)，(0,1,0)，(0,1,1)，(1,0,0)，(1,0,1)，(1,1,0)，(1,1,1)，可表示为一棵三层的二叉树。

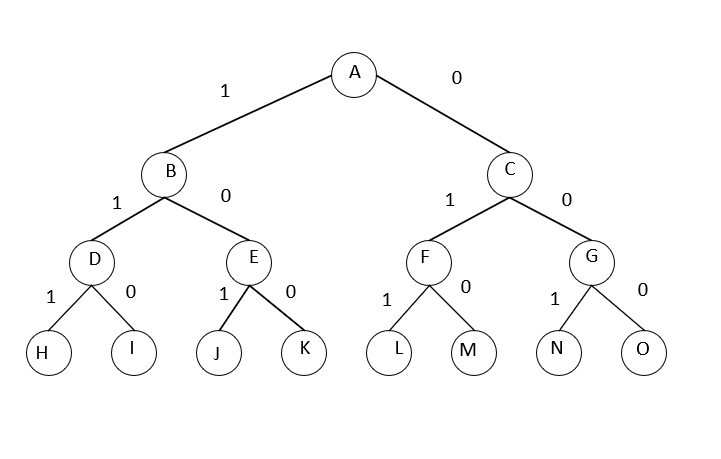
回溯法按深度优先策略从根开始向下搜索，当搜索到任一结点时，判断该结点是否满足约束条件：背包剩余载荷是否大于等于当前物体重量，满足就把当前物体加人背包；否则，跳过该结点以下的子树（剪枝），向上逐级回溯。

动态规划法

用来求解最优化问题。其思想是：化为多步决策，如果问题的最优解可以由子问题的最优解推导得到，则先求子问题的最优解，再由子问题的最优解构造原问题的最优解；若子问题有较多的重复出现，则可以自底向上，从最终子问题向原问题逐步求解。

实例：在多段图中找一条从 s 到 t 的最短路径。

算法思路：将问题化为多步决策，从最后一段开始向前依次计算各结点到 t 的最短路径。当第 i 层结点计算时，会用到上一层结点的计算结果，

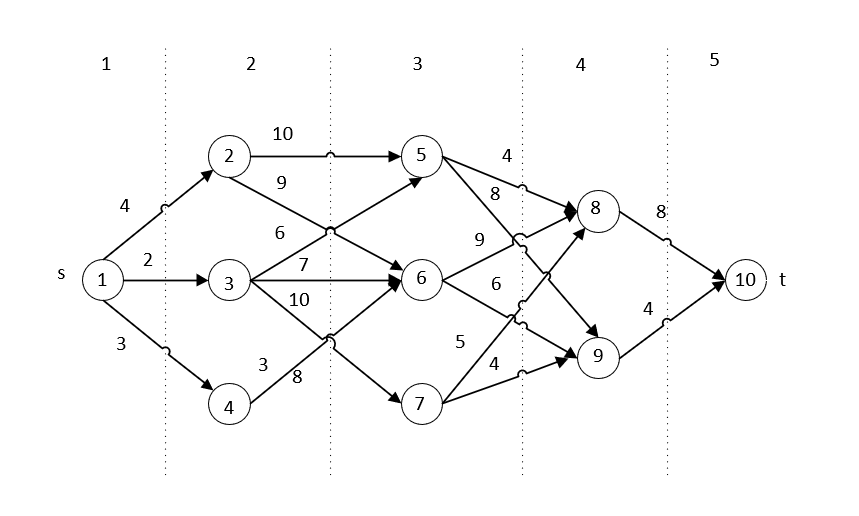
如图所示，先求 ⑧→t 和 ⑨→t 的最短路径，再求 ⑤→t、⑥→t、⑦→t 的最短路径，再求 ②→t、③→t、④→t 的最短路径，最后求 s一t 的最短路径。

例如，s 到 t 的最短路径应该是 s一②一1、s一③一1、s一④-t 这三条路径中的最短者，而 ②-1、③一、④一t 的最短路径在上一步中已经求出，可以直接利用。也就是说，在 ②→t、③→1、④一1 的最短路径基础上各增加一条边，那么 s→②→t、s→③→1、s一④→t 三者的最小者即为所求。

算法分析

算法的特征之一是有穷性，一个算法必须在有穷步执行后终止。但在实际应用中，仅要求算法能终止还远远不够，还需对算法的执行效率进一步分析，以确定算法能否有效地求得问题的解。有许多实际应用问题，理论上有计算机解，但求解所需的时间或空间耗费巨大，实际上无法办到；对有些时效性很强的问题，如实时控制，即使算法执行时间很短，如只有一两秒，也可能是无法忍受的。

如：给出 26 个英文字母的全排列。它的排列数为 26!≈4×10²⁶，以每年 365 天计算，每年 365×24×3600=3.1536x10⁷ 秒，以每秒能完成 10⁷ 个排列的超高速电子计算机来做这项工作，需要4×10²⁶/(3.1536x10¹⁴)=1.2x10¹² 年。

显然，以计算机的运行速度是不可能实现的。算法分析就是对执行该算法所消耗的计算机资源进行估算。一个算法所需的资源越多，它的复杂性越高，反之则低。算法设计的目标是设计复杂性尽可能低的算法。

计算机资源中最重要的是时间和空间资源：时间复杂性指一个算法在计算机上运算所花费的时间；空间复杂性指一个算法在计算机上运算所花费的空间。

对算法的时间复杂性进行分析就是统计算法中各种操作的执行时间，即包括哪些基本运算（如赋值、加、减、乘、除等），每种运算执行的次数，该运算执行一次所花费的单位时间等。

一个算法的执行时间 = 算法运行时所执行的每条语句的执行时间总和

算法分析举例，如表所示：

算法分析举例
项目	算法 1	算法 2	算法 3
包含语句	x←x＋y	for i←1 to n do x←x＋y	for i←1 to n do for j←1 to n do x←x＋y
语句执行次数	x←x＋y 执行了 1 次	x←x＋y 执行了 n 次	x←x＋y 执行了 n² 次
运算量	加法一次，赋值一次	加法 n 次，赋值 n 次	加法 n² 次，赋值 n² 次