[优选算法专题六.模拟 ——NO.37~39 替换所有的问号、提莫攻击、Z 字形变换]

题目链接

1576. 替换所有的问号

题目描述

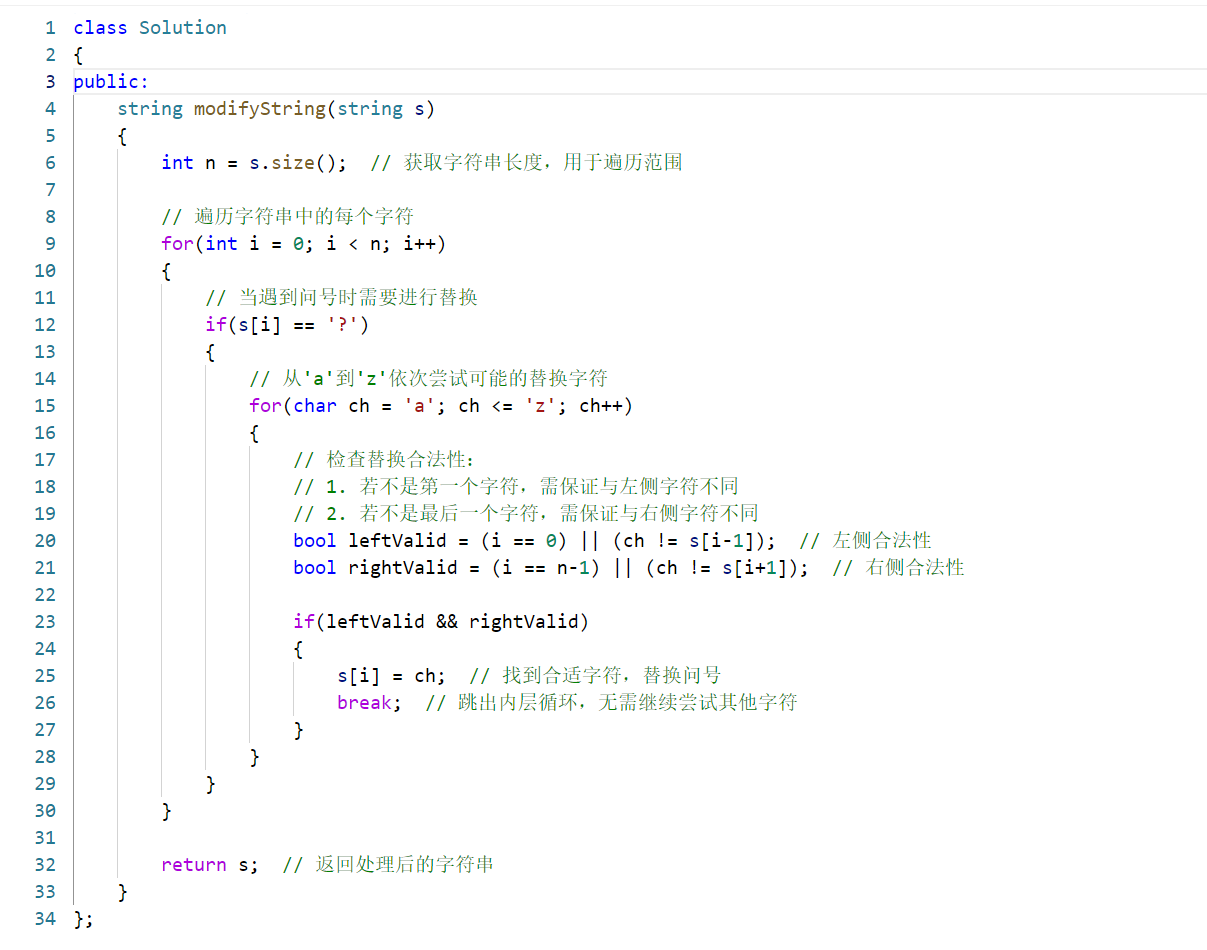
核心思路

遍历字符串中的每个字符，当遇到问号 '?' 时，从 'a' 到 'z' 依次尝试替换，选择一个既不等于左侧字符（如果存在）也不等于右侧字符（如果存在）的字符作为替换值。这样可以保证替换后不会出现连续相同的字符。

题目解析

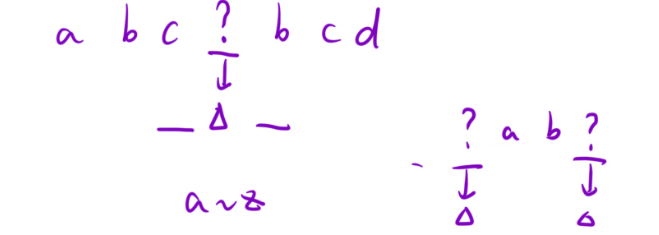
• 时间复杂度：O(n)，其中 n 是字符串长度。每个 '?' 最多尝试 3 个字母即可找到合法替换（因为英文字母有 26 个，而相邻字符最多 2 个不同值，必然存在至少 1 个合法字母），因此整体遍历次数与 n 成正比。
• 空间复杂度：O(1)，仅使用常数级额外空间（无需额外数据结构）。

---

题目链接：

495. 提莫攻击

题目描述：

题目解析：

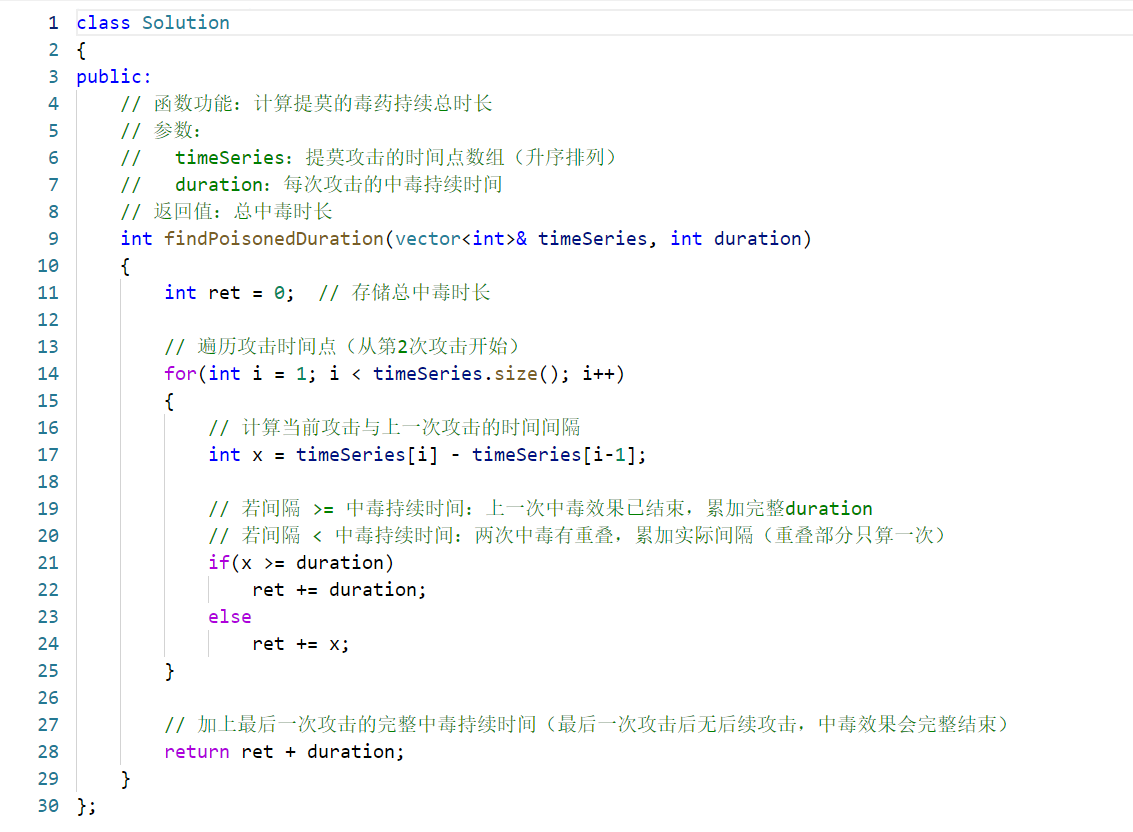
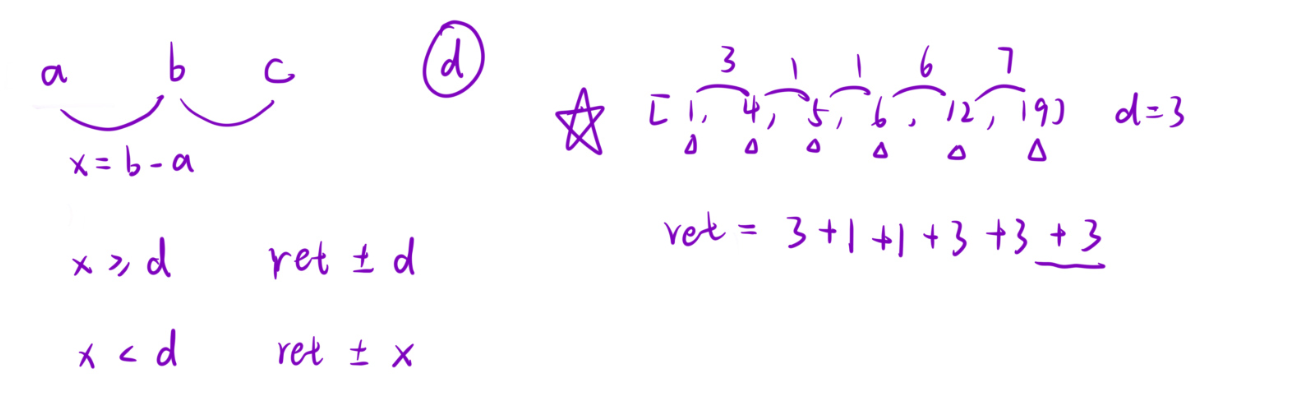
核心问题

计算提莫多次攻击后，目标的总中毒时长。关键在于处理攻击时间重叠的情况：如果两次攻击间隔小于中毒持续时间，重叠部分的中毒时间只能算一次。

逻辑分析

1. 单次攻击的基础时长：每次攻击会使目标中毒 duration 单位时间，但若下一次攻击在中毒结束前发生，重叠部分不重复计算。

2. 间隔与重叠的处理：

   • 设两次攻击时间为 t[i-1] 和 t[i]，间隔为 x = t[i] - t[i-1]。
   • 若 x >= duration：前一次中毒在第二次攻击前已结束，贡献 duration 时长。
   • 若 x < duration：两次中毒重叠，前一次实际贡献 x 时长（重叠部分被后一次攻击覆盖）。

3. 最后一次攻击：最后一次攻击后无后续攻击，其完整的 duration 时长需单独累加。

示例说明

• 输入：timeSeries = [1,4], duration = 2

  • 第一次攻击（1）到第二次攻击（4）的间隔 x=3，大于 duration=2，因此第一次贡献 2 时长。
  • 加上最后一次攻击的 2 时长，总时长为 2 + 2 = 4。

• 输入：timeSeries = [1,2], duration = 2

  • 间隔 x=1 < 2，第一次贡献 1 时长。
  • 加上最后一次的 2 时长，总时长为 1 + 2 = 3。

复杂度分析

• 时间复杂度：O(n)，其中 n 是攻击次数，只需遍历一次数组。
• 空间复杂度：O(1)，仅使用常数额外空间。

---

题目链接

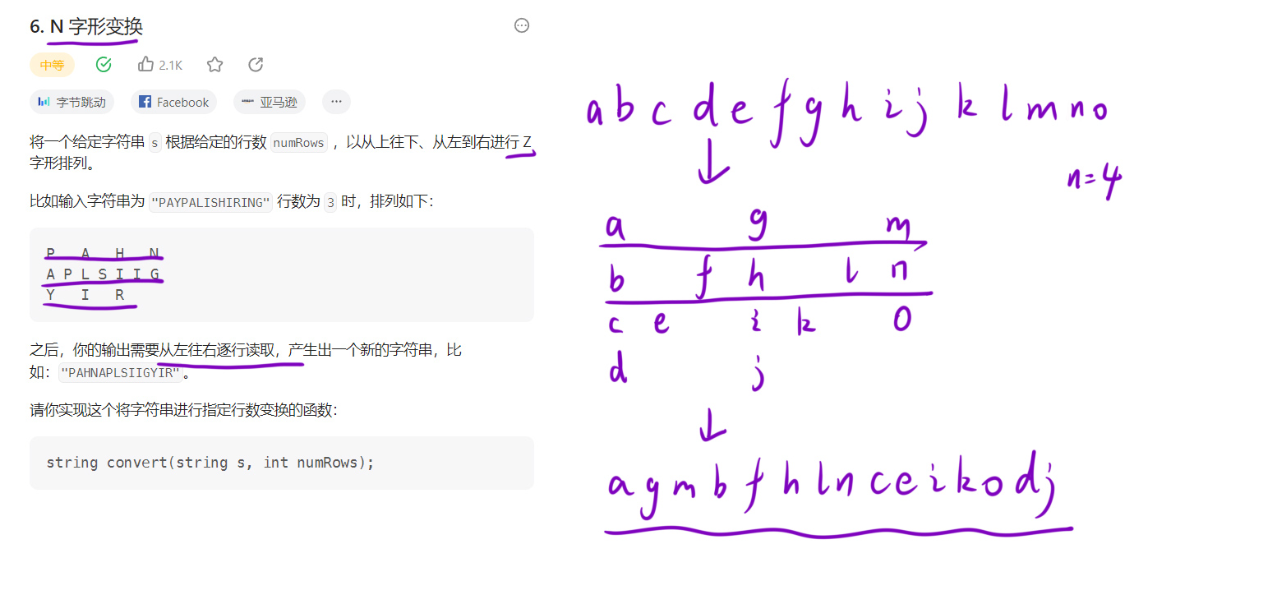
6. Z 字形变换

题目描述：

题目解析：

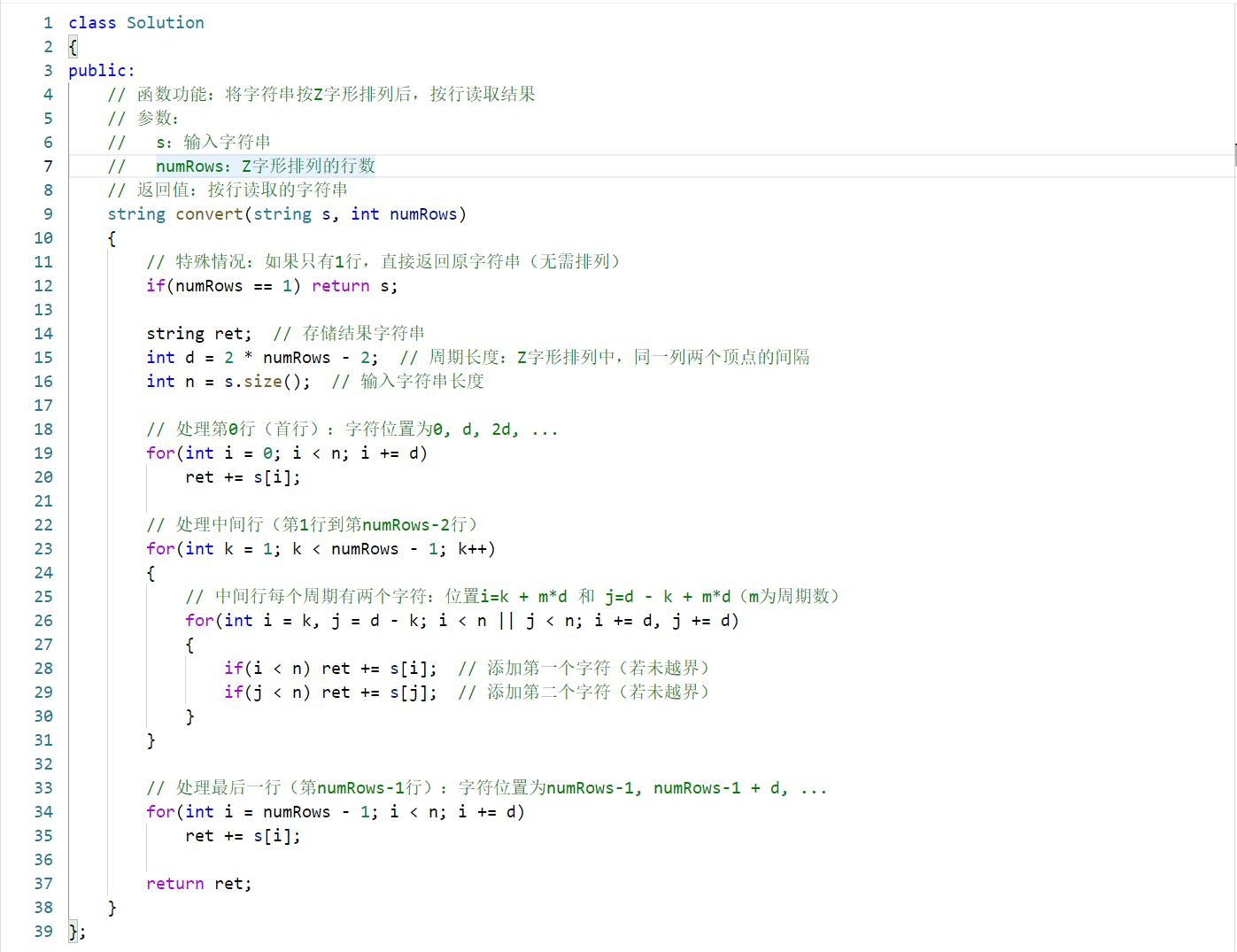
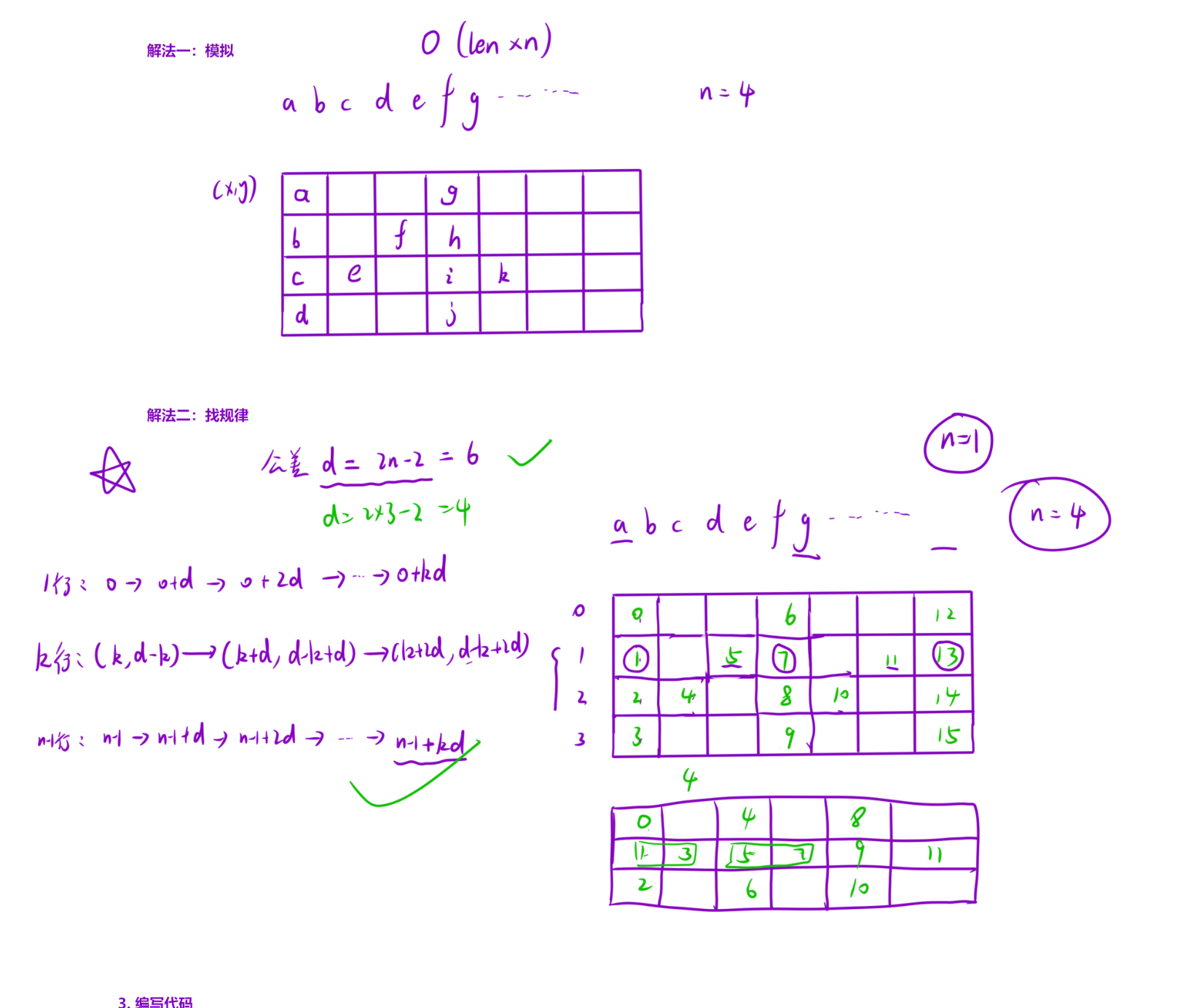
逻辑分析

1. Z 字形排列的周期规律：Z 字形排列可看作重复的「下降 - 上升」周期，每个周期的长度为 d = 2 * numRows - 2（例如 3 行时，d=4）。

2. 各行字符位置规律：

   • 首行（第 0 行）：字符位置为 0, d, 2d, 3d, ...（每个周期的起点）。
   • 末行（第 numRows-1 行）：字符位置为 numRows-1, numRows-1 + d, numRows-1 + 2d, ...（每个周期的终点）。
   • 中间行（第 k 行，1≤k≤numRows-2）：每个周期有两个字符，位置分别为 k + m*d 和 (d - k) + m*d（m 为周期数）。

3. 特殊情况处理：当 numRows=1 时，字符串无需排列，直接返回原字符串。

示例说明

以 s = "PAYPALISHIRING", numRows = 3 为例：

• d = 2*3 - 2 = 4。
• 首行（k=0）：位置 0,4,8,12 → 字符 P,A,H,N。
• 中间行（k=1）：每个周期的两个位置为 1+4m 和 3+4m → 字符 A,P,L,S,I,I,G。
• 末行（k=2）：位置 2,6,10 → 字符 Y,I,R。
• 拼接后结果为 "PAHNAPLSIIGYIR"。

复杂度分析

• 时间复杂度：O(n)，其中 n 是字符串长度，每个字符仅被访问一次。
• 空间复杂度：O(n)，用于存储结果字符串（不考虑输出空间时为 O(1)）。