Java基础——集合进阶用到的数据结构知识点4
一、数据结构
1.1 背景
红黑树为何而生?—— 需求背景
❌ AVL 树的痛点:频繁旋转
- AVL 树追求“严格平衡” → 每次插入/删除都可能触发多次旋转
- 虽然查询快,但插入/删除代价高
- 不适合频繁修改的场景(如数据库索引、内存映射表)
✅ 红黑树的诞生目标:
在保证“近似平衡”的前提下,减少旋转次数,提高插入/删除效率
💡 类比:
| 数据结构 | 平衡程度 | 查询速度 | 插入/删除速度 |
|---|---|---|---|
| BST | 无 | O(n) | O(n) |
| AVL | 严格 | O(log n) | 较慢(多旋) |
| 红黑树 | 近似 | O(log n) | 较快(少旋) |
✅ 红黑树是工程中的“折中之选” —— 它允许轻微不平衡,但确保最坏情况下仍为 O(log n)
1.2 红黑树
1.1.1 什么是红黑树?—— 定义与本质
红黑树是一种自平衡的二叉查找树(BST),通过给每个节点附加一个颜色属性(红色或黑色),在插入和删除时通过“变色”和“旋转”来维持近似平衡。
- 红黑树 是一种二叉树,用于内存中(如 Java 的
TreeMap、TreeSet)
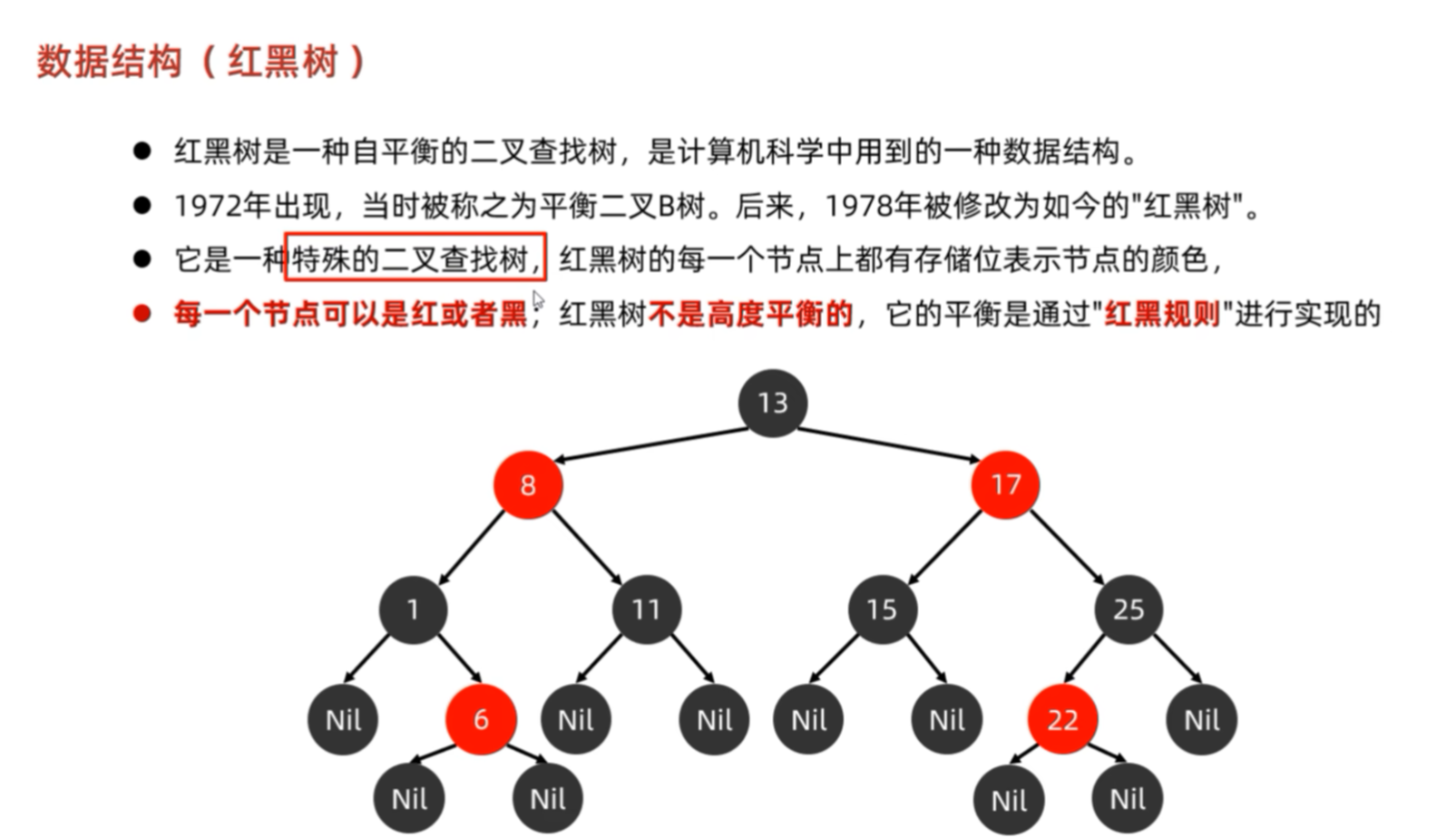
红黑树是一种特殊的二叉查找树,但是不是平衡二叉树,跟它还是有区别的。

1.1.2 红黑树的五大规则(必须牢记!)
所有红黑树都必须满足以下五条规则,否则就不是合法的红黑树。
📌 记忆口诀:“根黑、不连红、黑深同、叶黑、红子黑”

✅ 这些规则共同保证了:任意路径长度 ≤ 2 × 黑高度 → 最坏情况 O(log n)
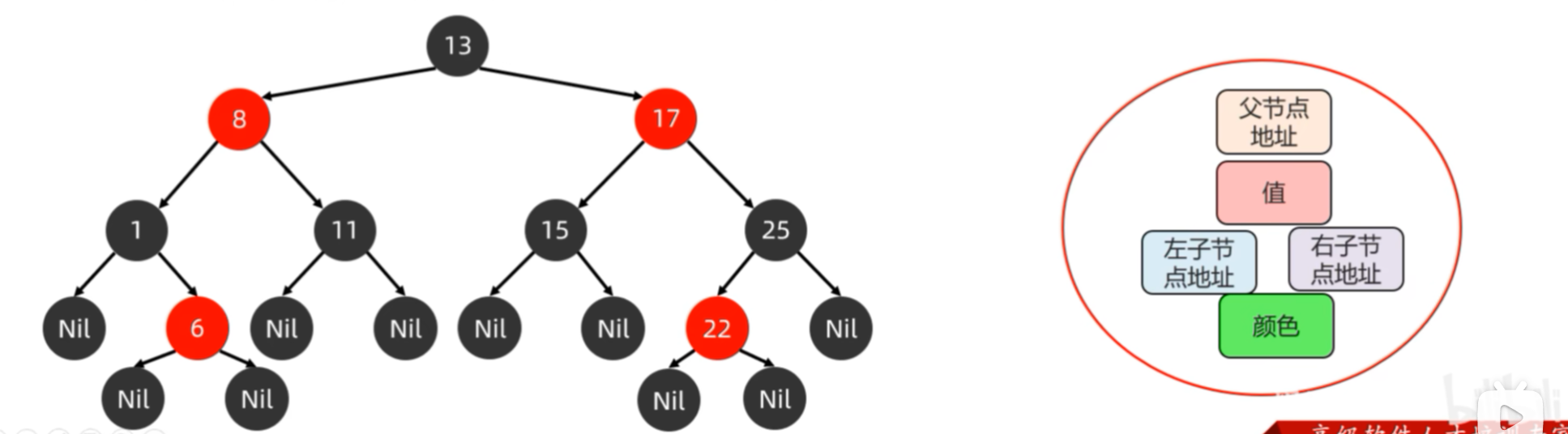
在红黑树的节点定义中,多了一个变量用以记录节点的颜色。
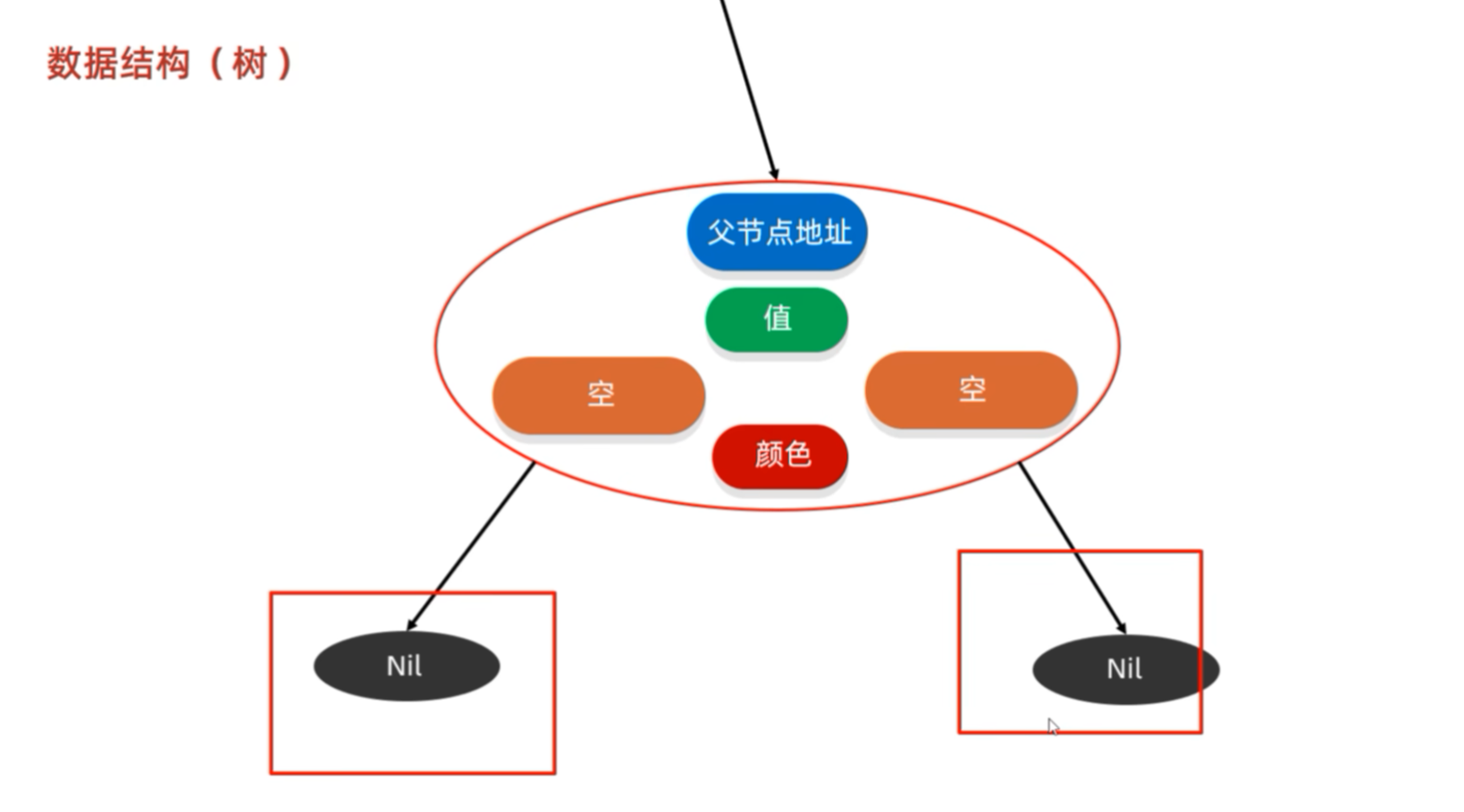
叶子节点里面是没有任何数据的,存储的都是NULL。这些叶子节点其实也是没有什么意义的,平时在查询数据或者遍历红黑树的时候也不会去考虑叶子节点,只是在红黑规则的规定上(如规则5)有些许作用。
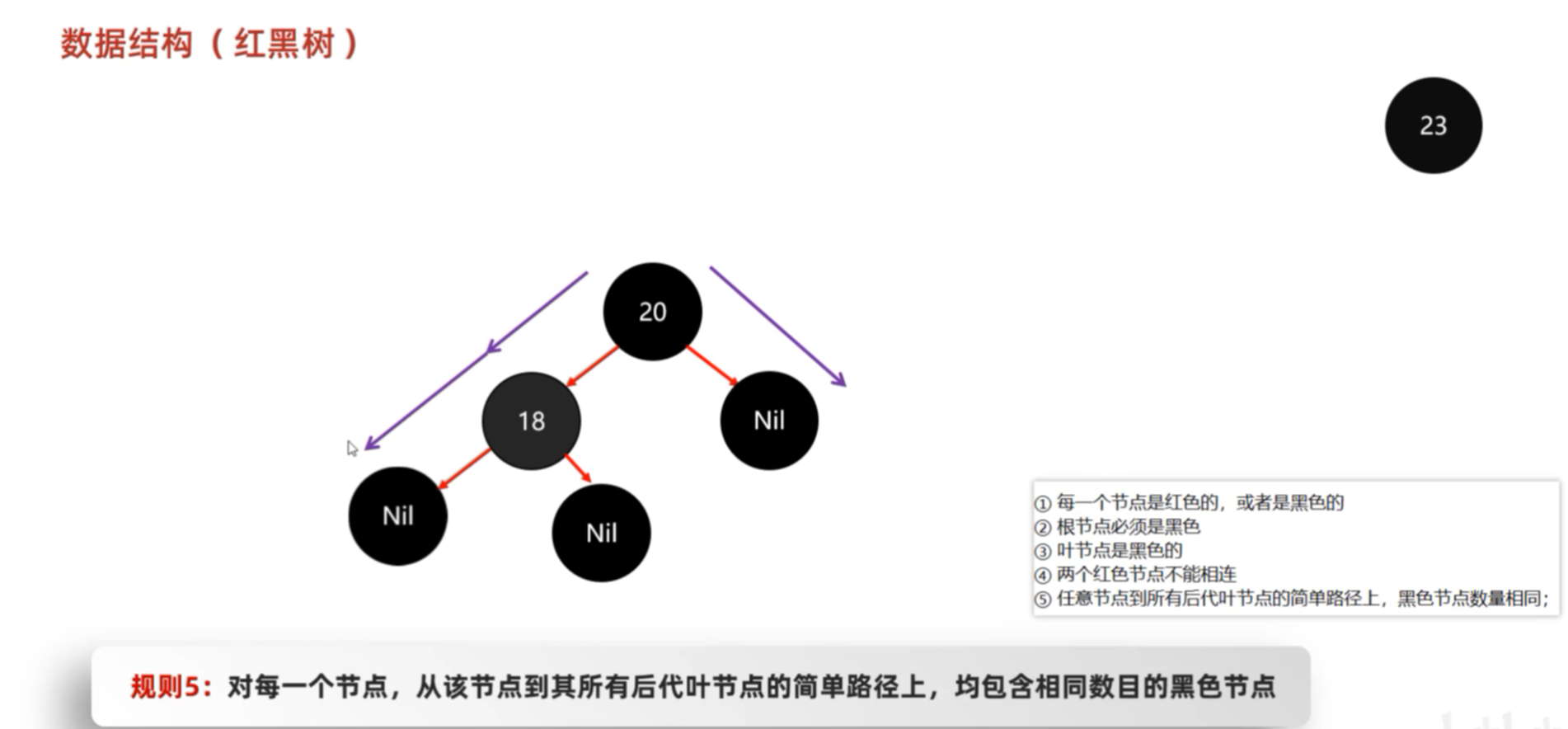
后代:对于13节点来说,下面全部的节点都是它的后代。17节点来说左右子节点的所有节点都是它的后代,它的兄弟节点8的所有后代节点都跟它没有关系。其后代节点中的叶子节点就是后代叶子节点。
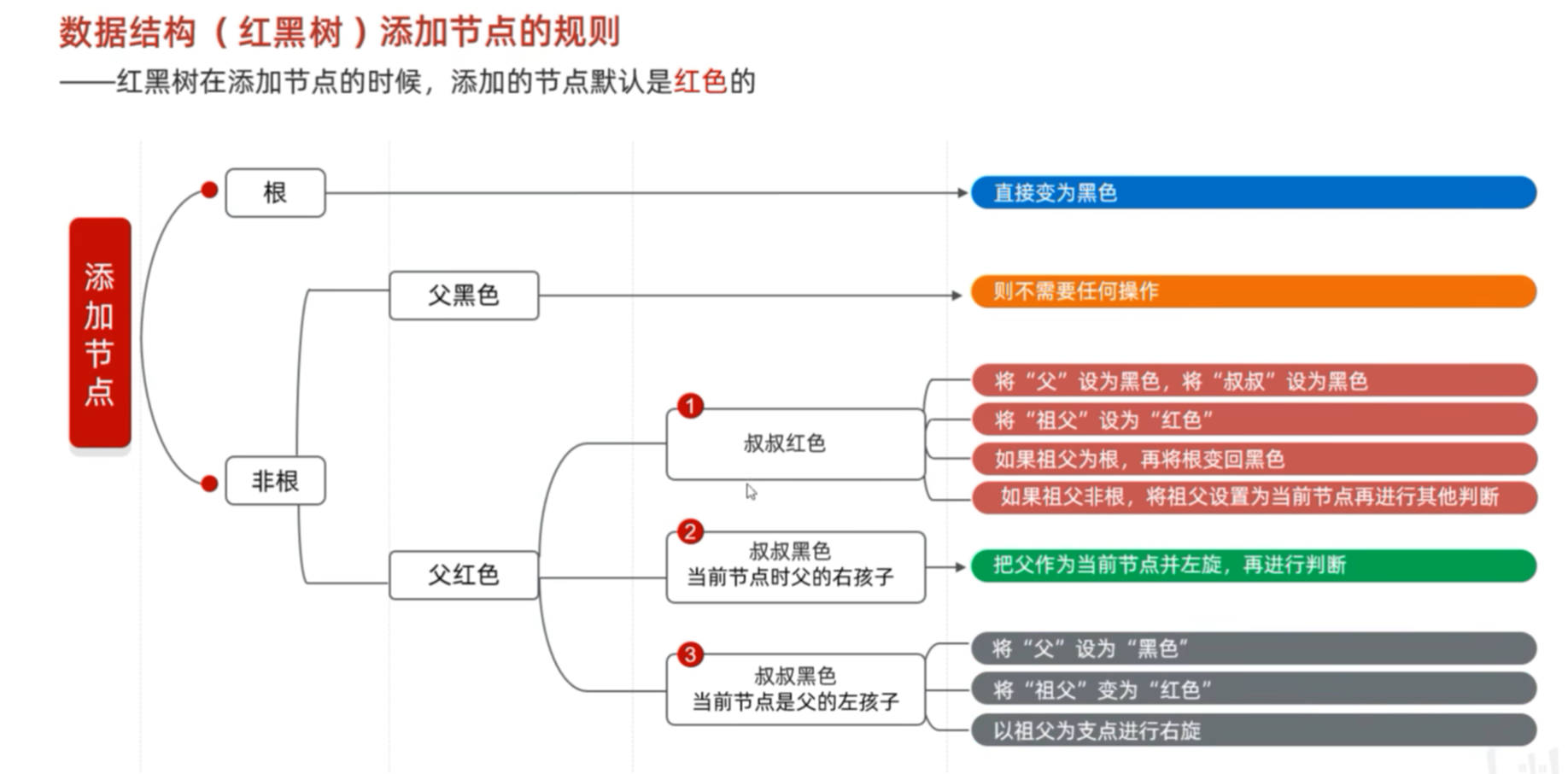
1.1.3 红黑树插入节点的规则
为什么默认节点的颜色是红色的好?现在举个反例假设都默认是黑色,来看这三个数据的排列。
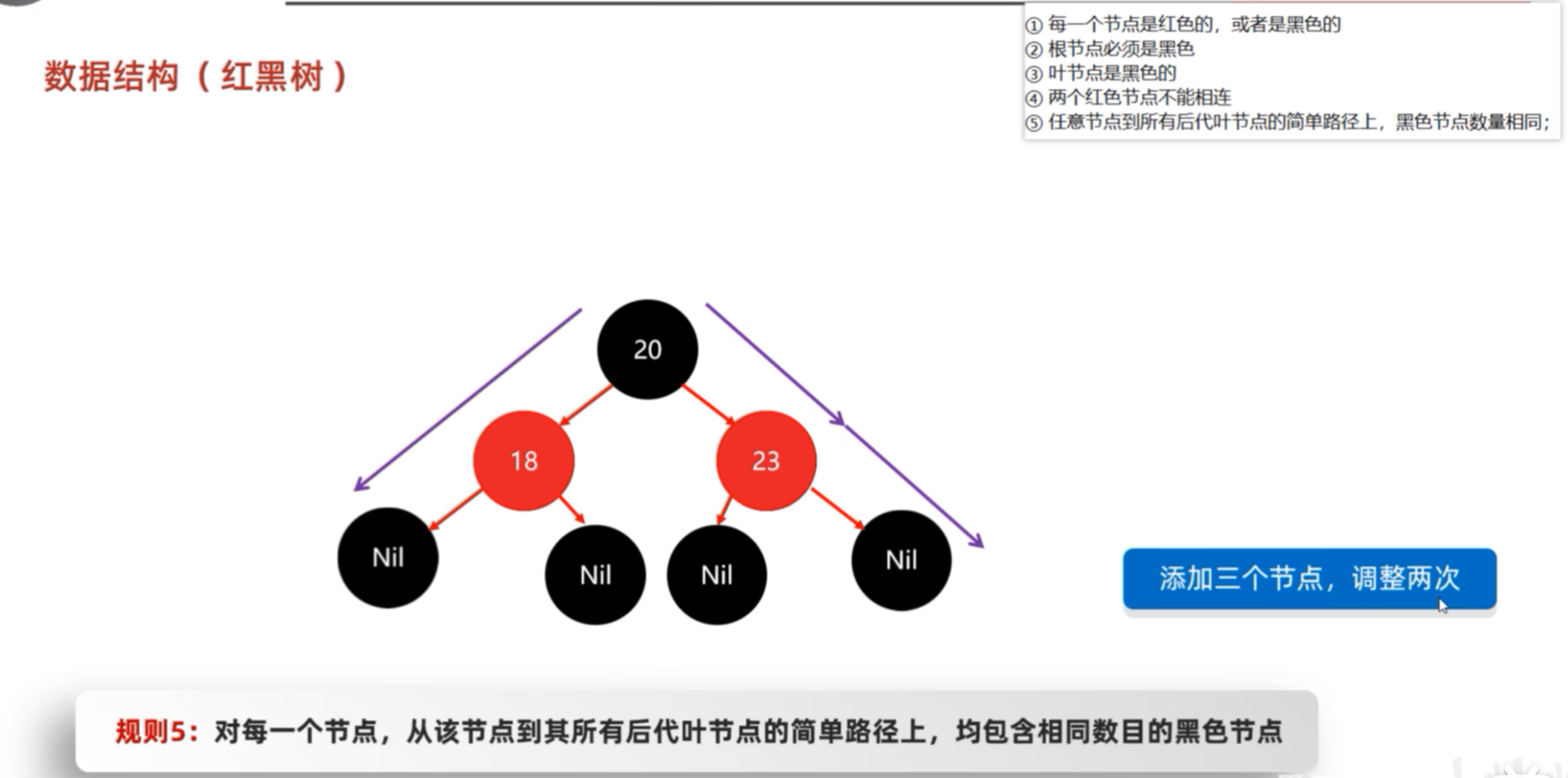
完整介绍:
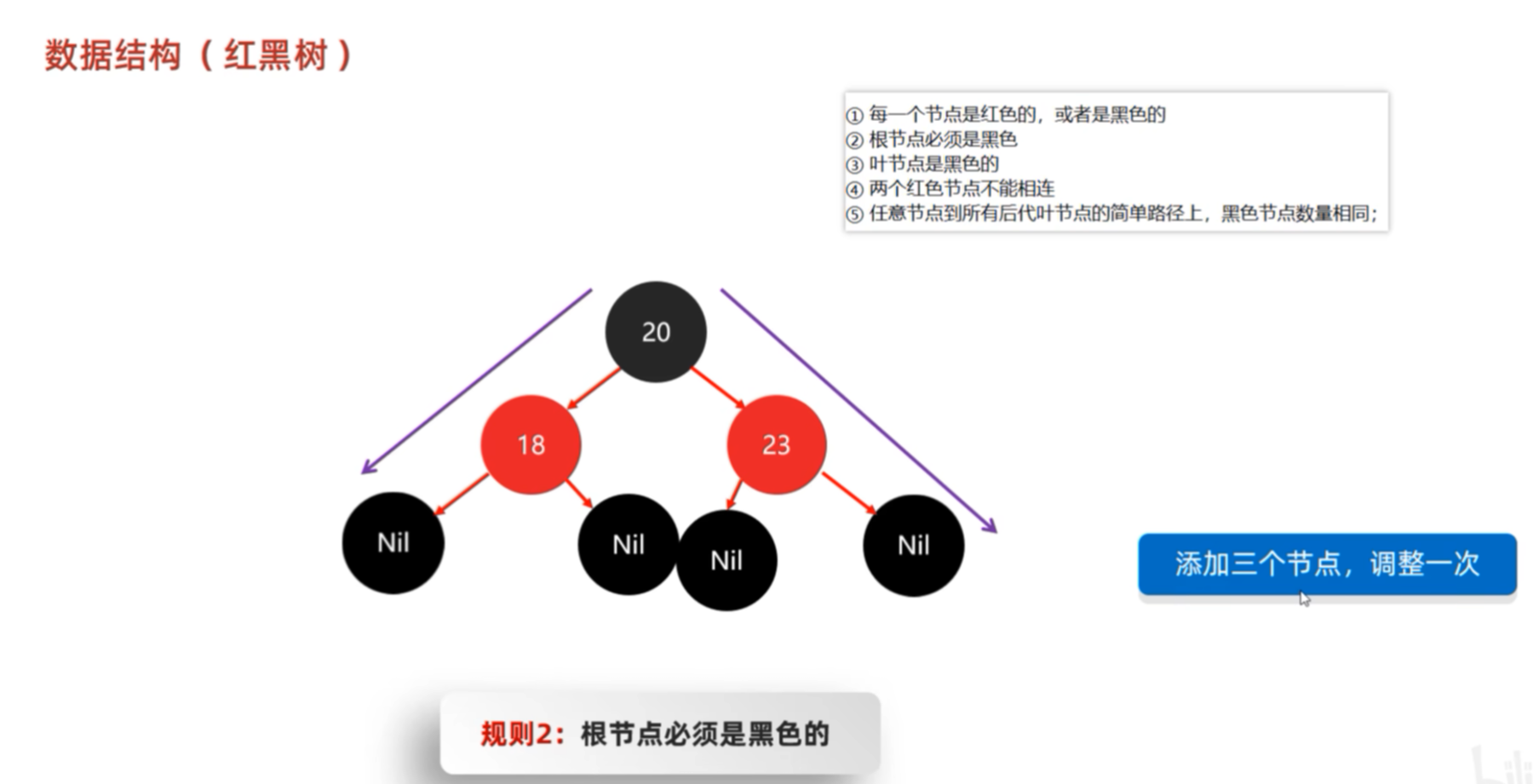
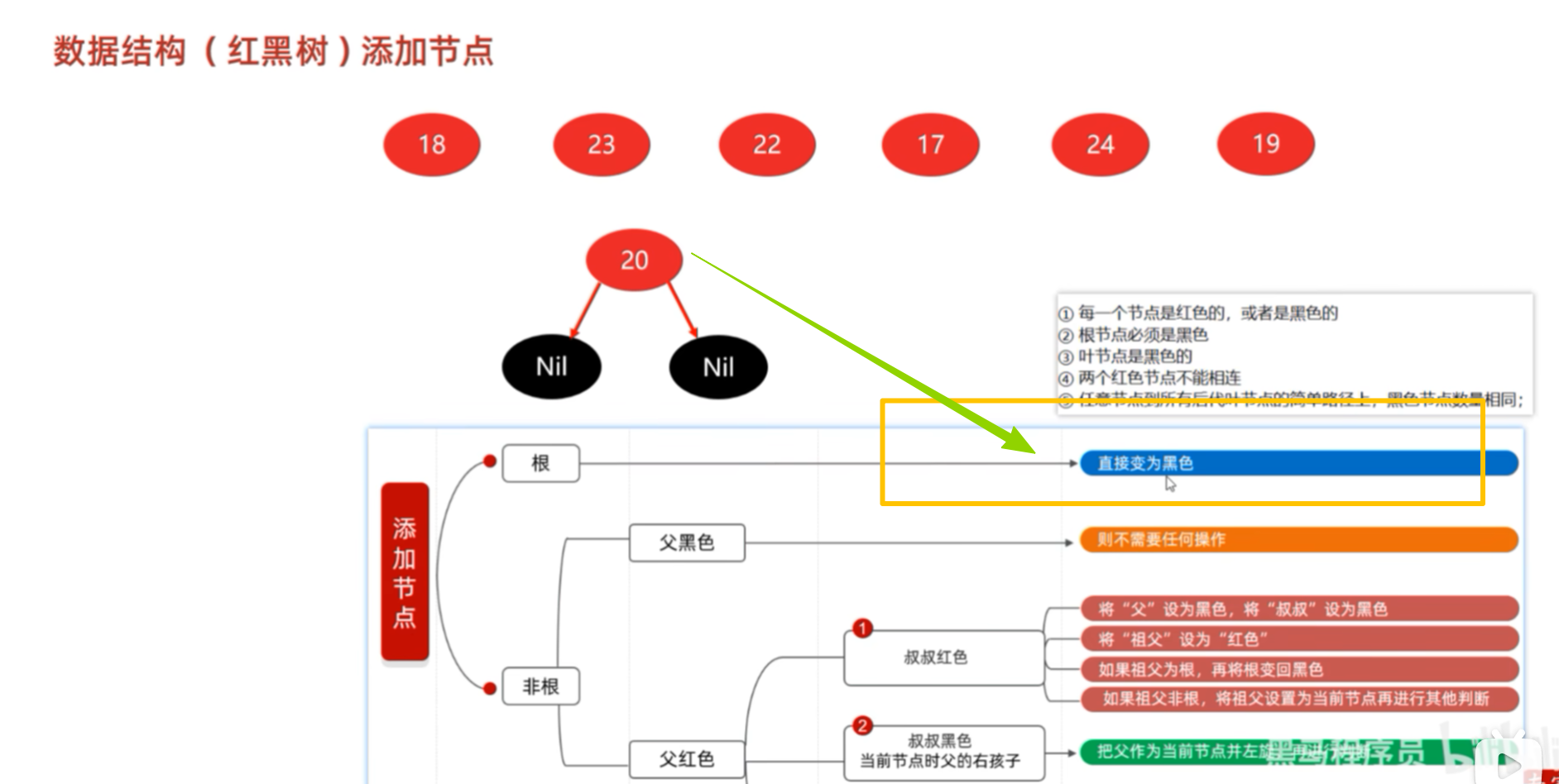
假设添加7个数据,第一次添加20作为根节点,触发违法规则2:根节点必须是黑色的。解决方案:黄色框中的文字。将其变成黑色。
接下来插入18,与20比较发现比其小,成为其左子节点,没有违反任何的规则。
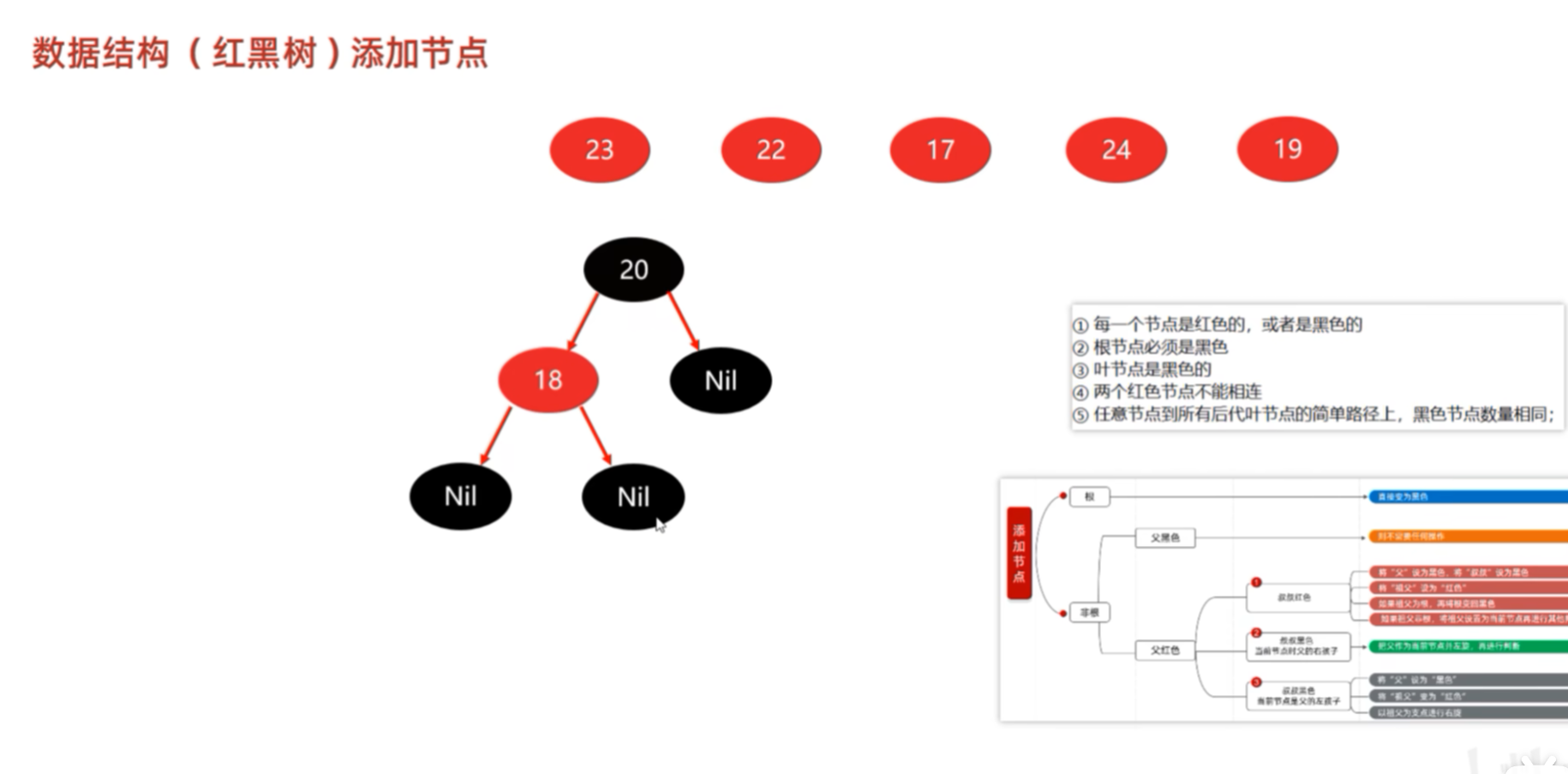
添加23,也没有违法红黑树的规则,
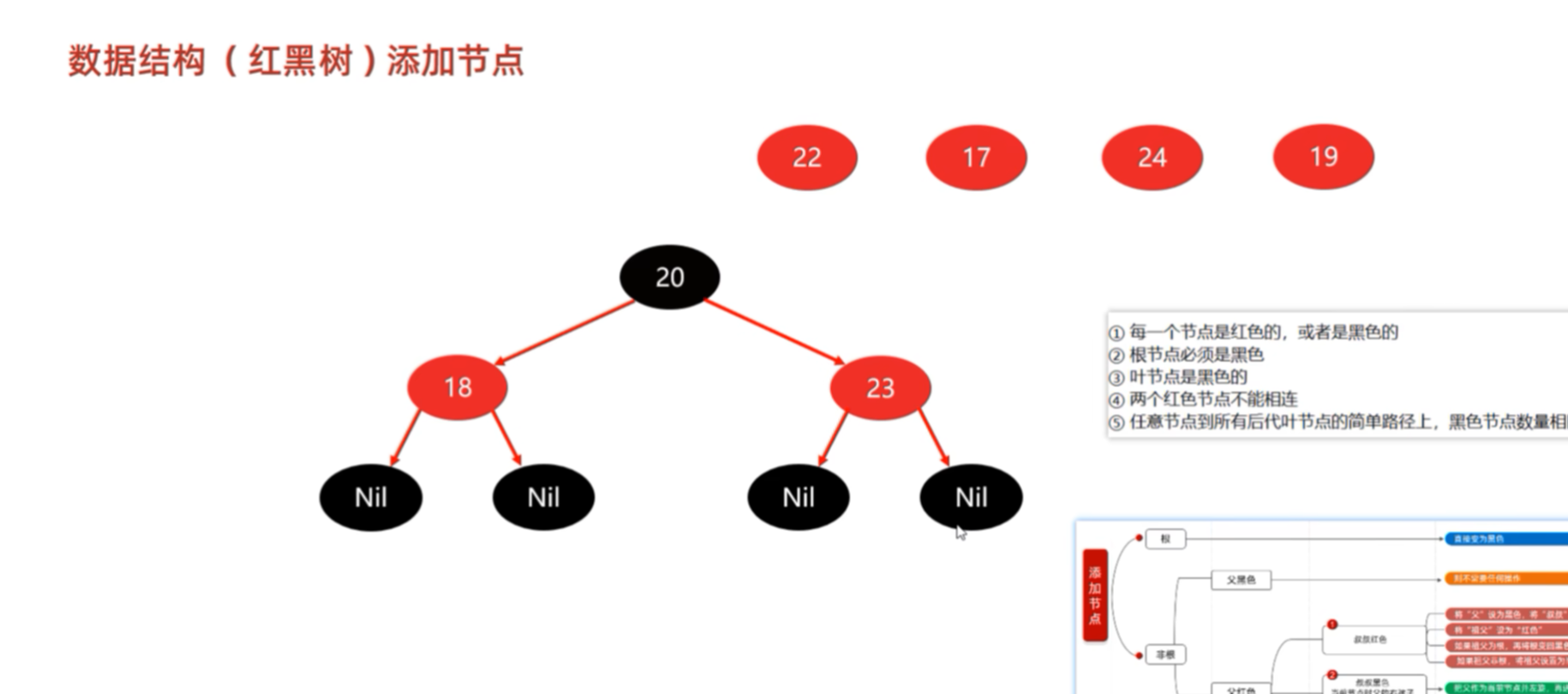
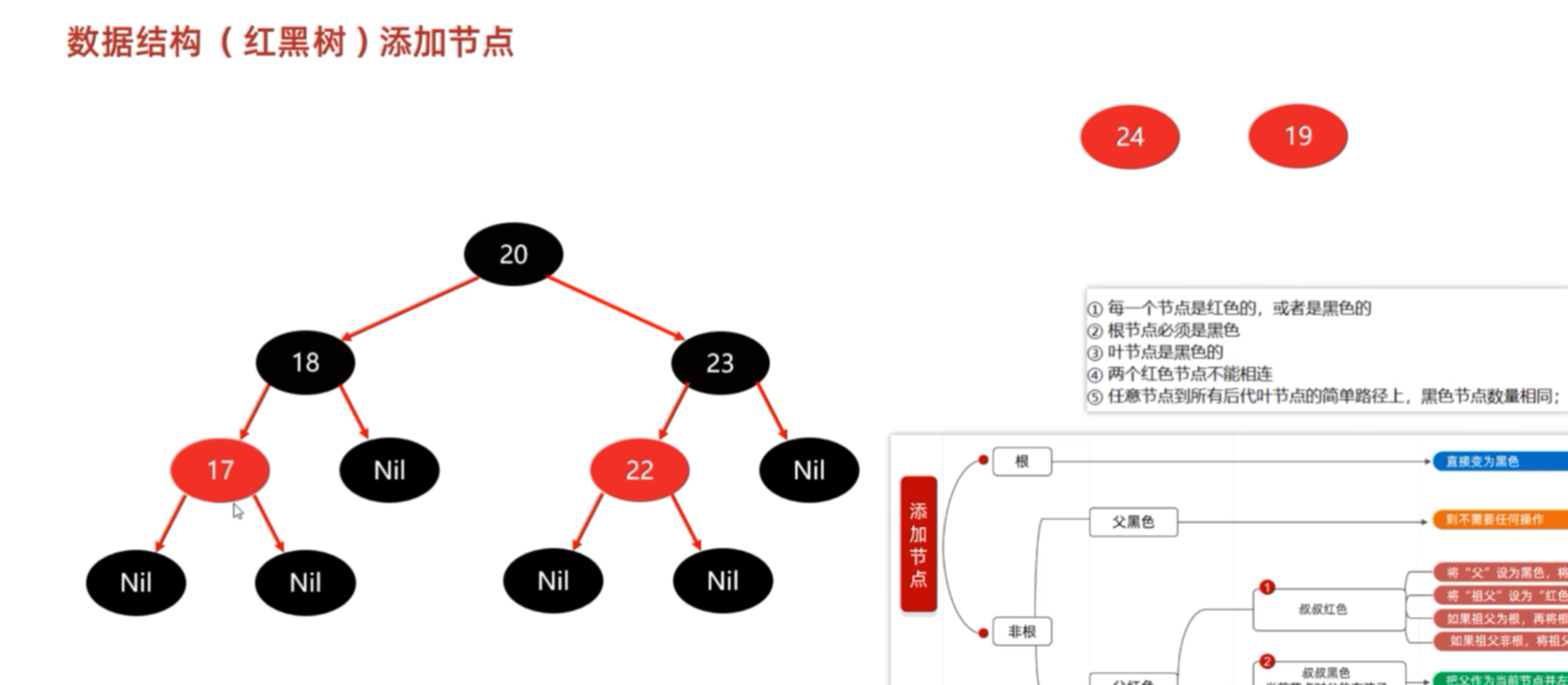
添加第四个节点22,22比根节点20要大,使其成为根节点的右子节点,发现已经有了右子节点23,与其比较,发现小,则成为23节点的左子节点。显然,违法了红黑树规则的第四条:两个红色的节点不能连续在一起。

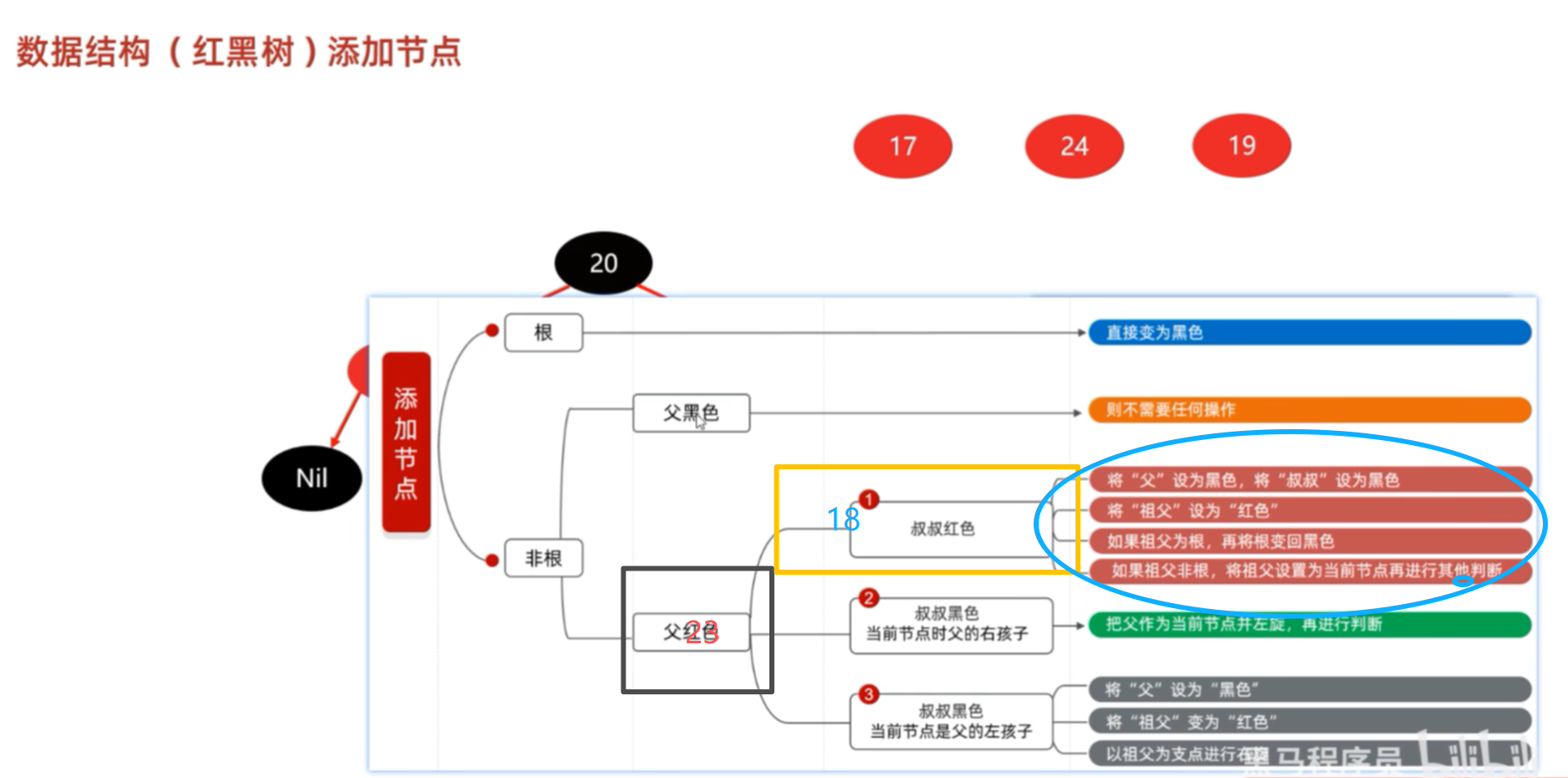
处理方案:①首先需要将“父”23节点设置为黑色,还需要把叔叔节点18设置为黑色;
②再将祖父也就是根节点20设置为红色;
③触发第三步,这里的祖父就是根节点,需要将其再变为黑色;
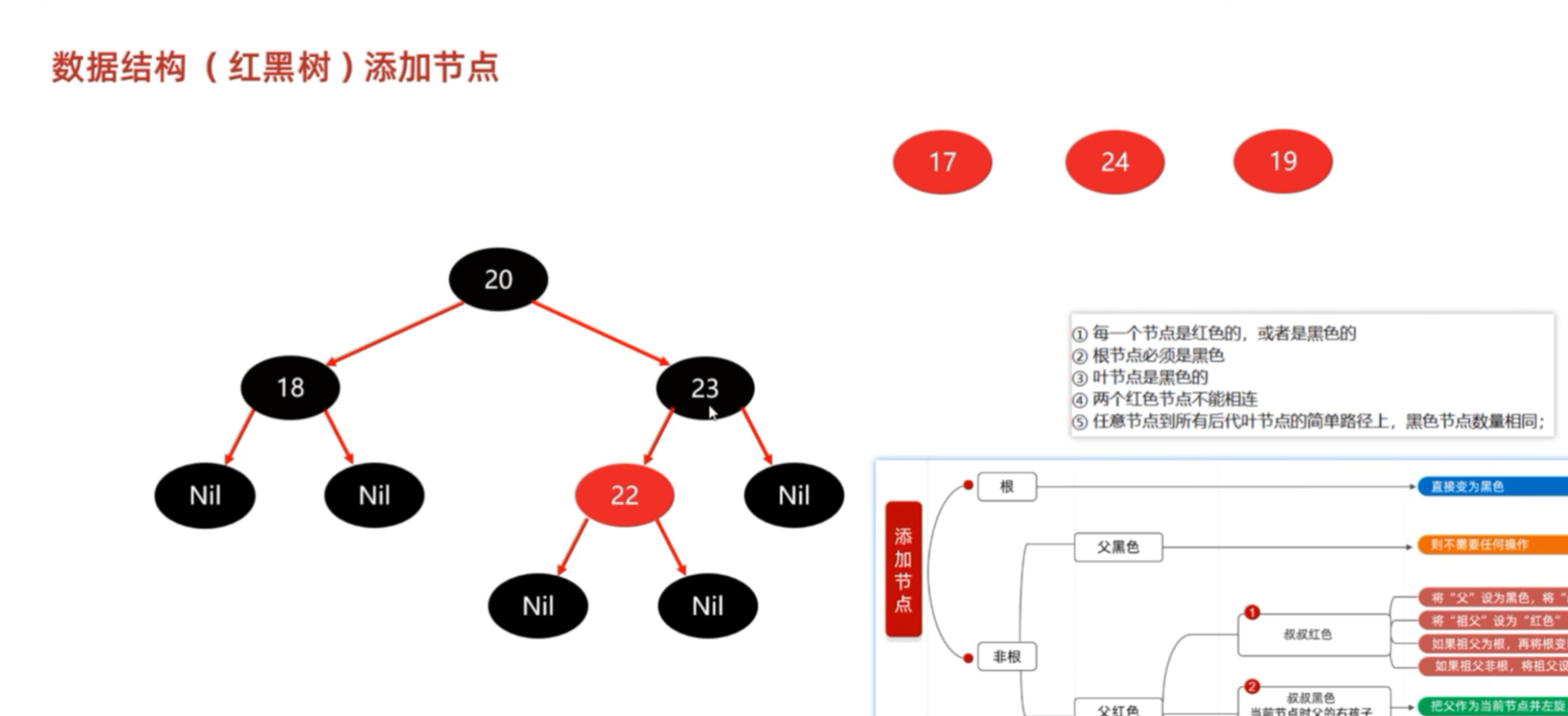
添加17,17比根节点20要小,使其成为左子节点,与其18比较,又成为其左子节点。没有违法任何的红黑树的规则,不需要进行任何的操作。
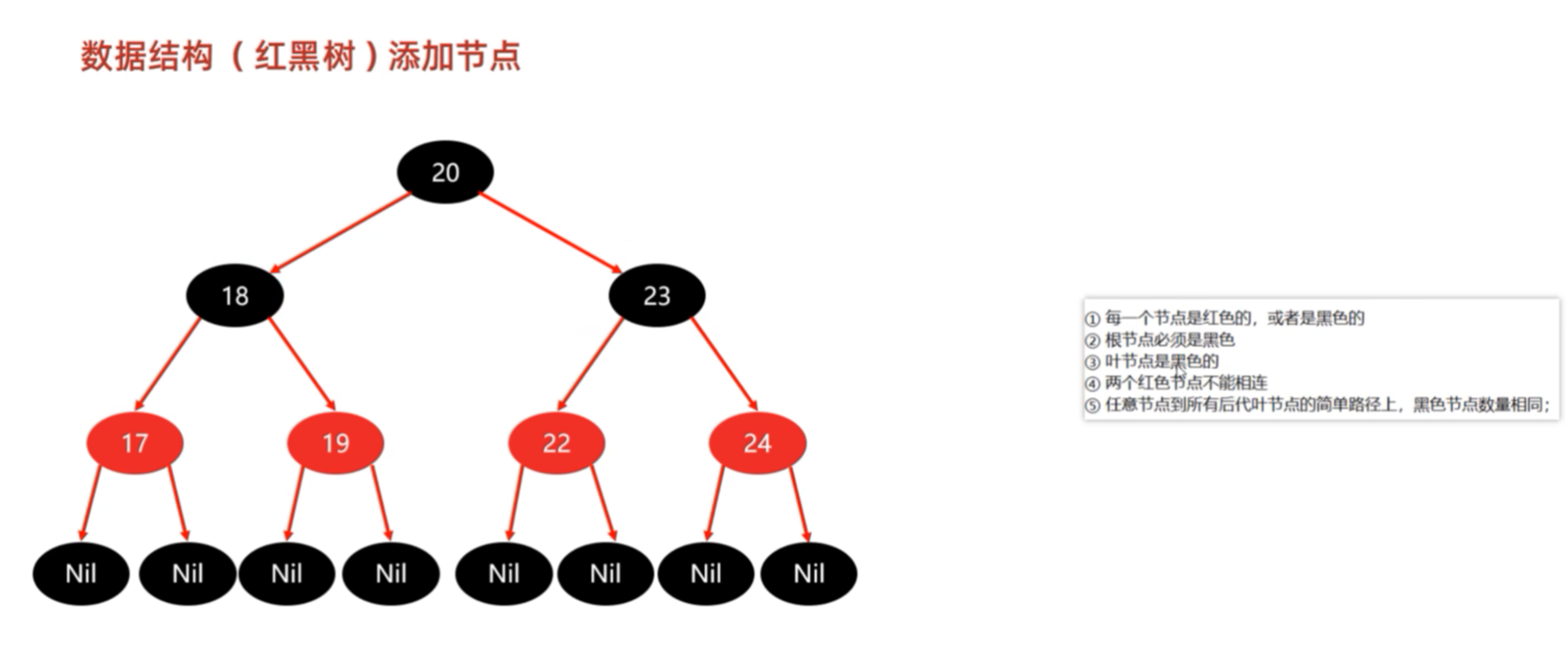
后续的数据也不需要进行任何的调正,没有违法规则。
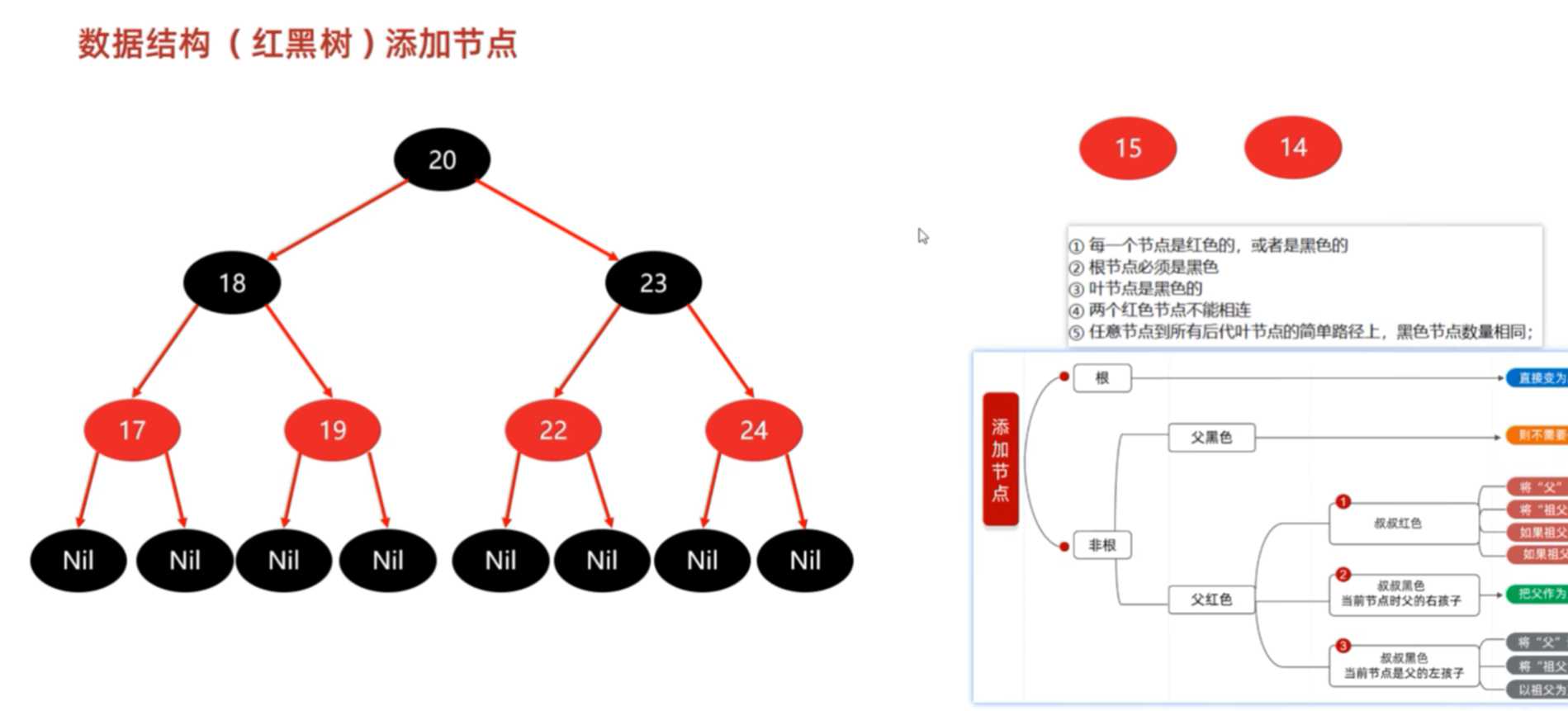
接下来添加15节点和14节点
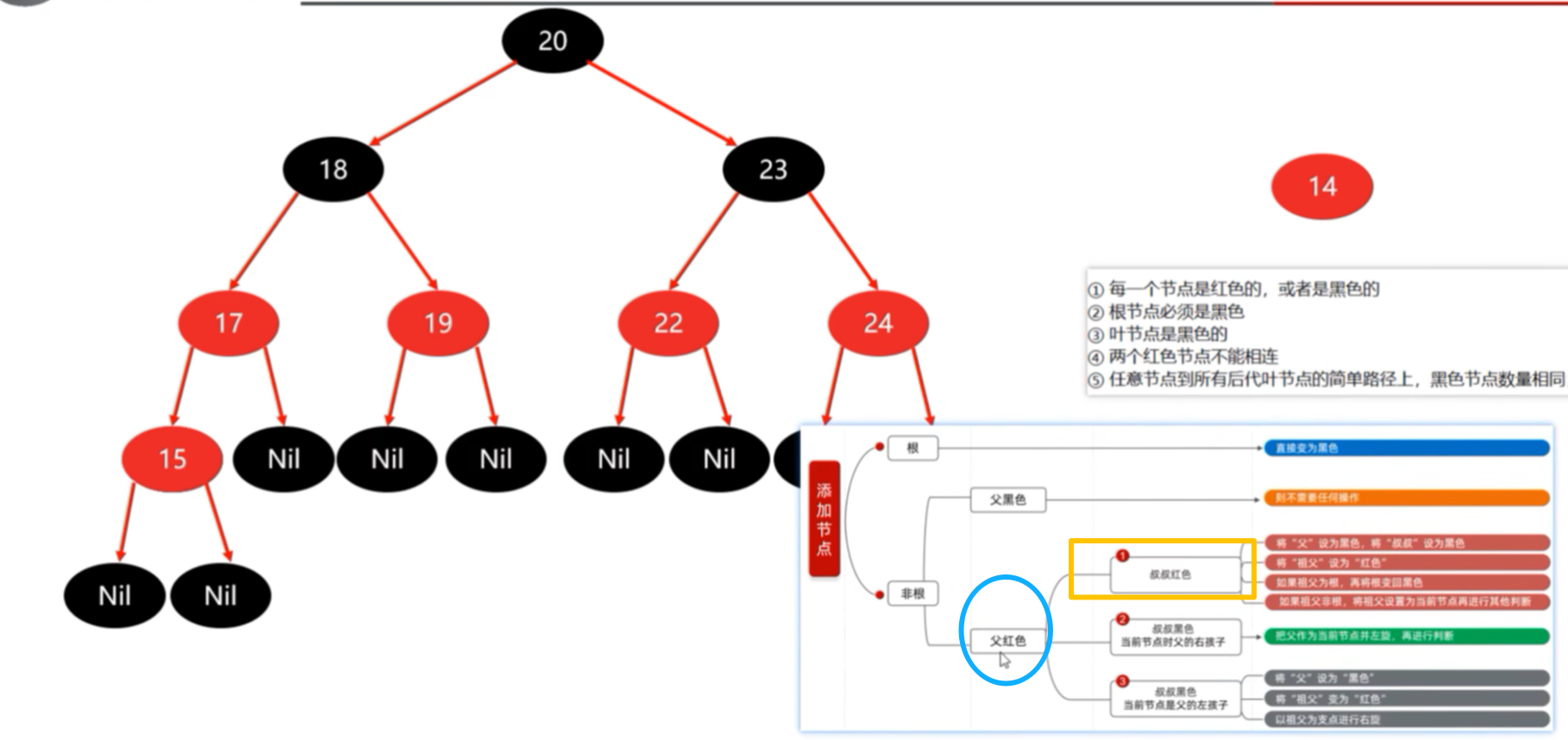
前三步骤完成:最后处理,其祖父18不是根节点,我们要在祖父节点18上再次进行判断。把它当成是当前节点,其18的父节点20是黑色的,不需要进行任何操作。
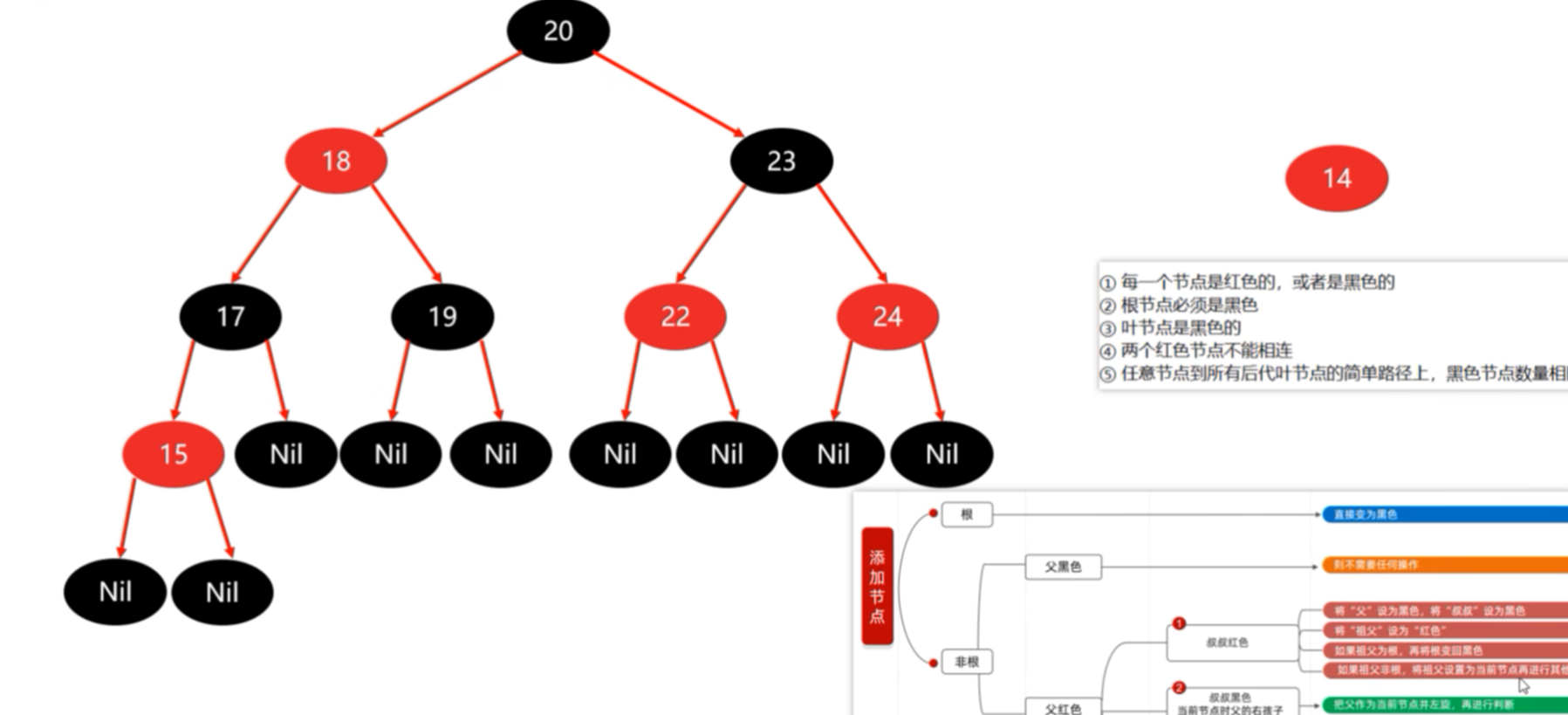
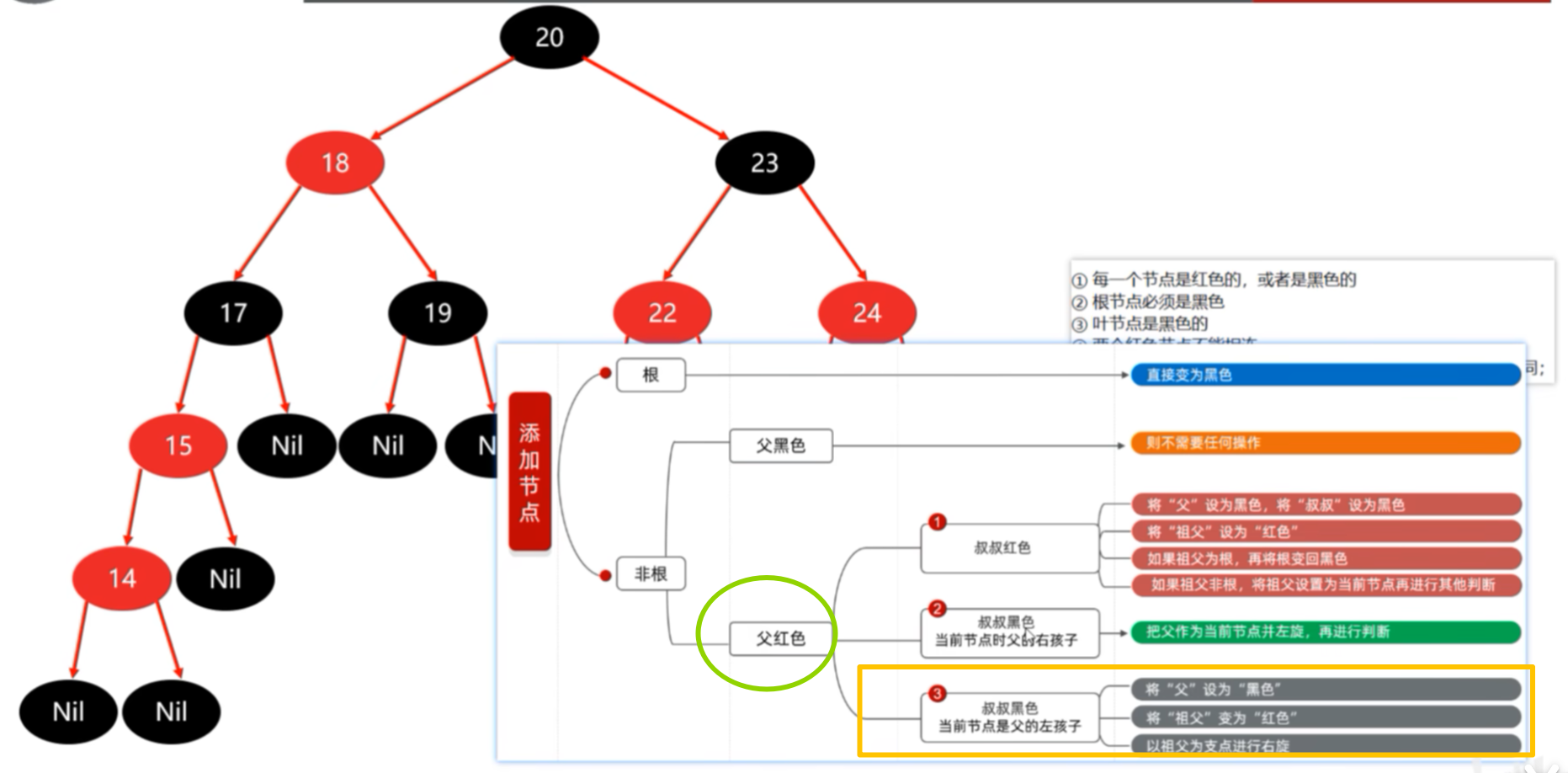
添加14:父节点15变成黑色,祖父节点17变成红色,再以祖父节点作为支点进行右旋。
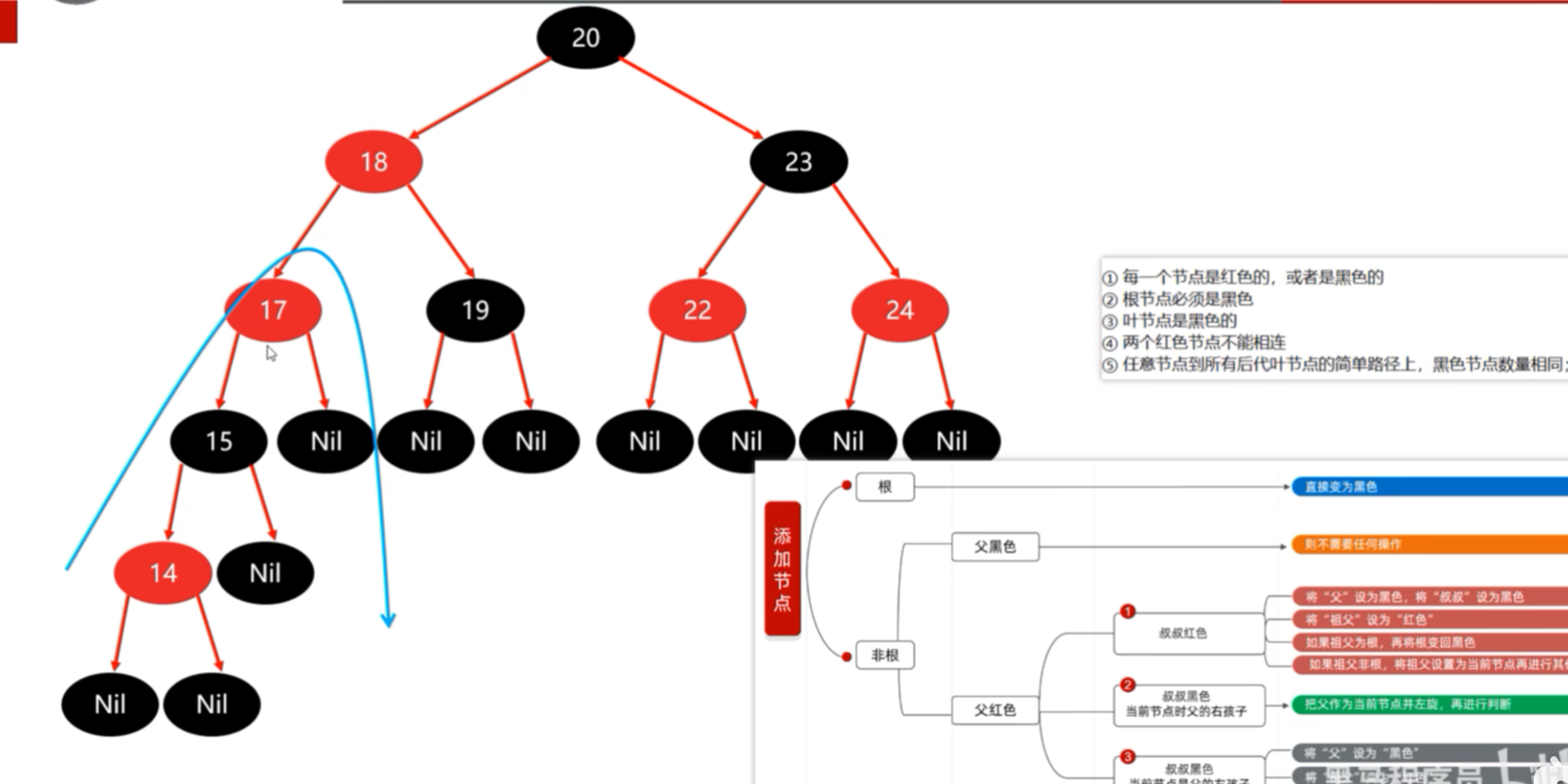
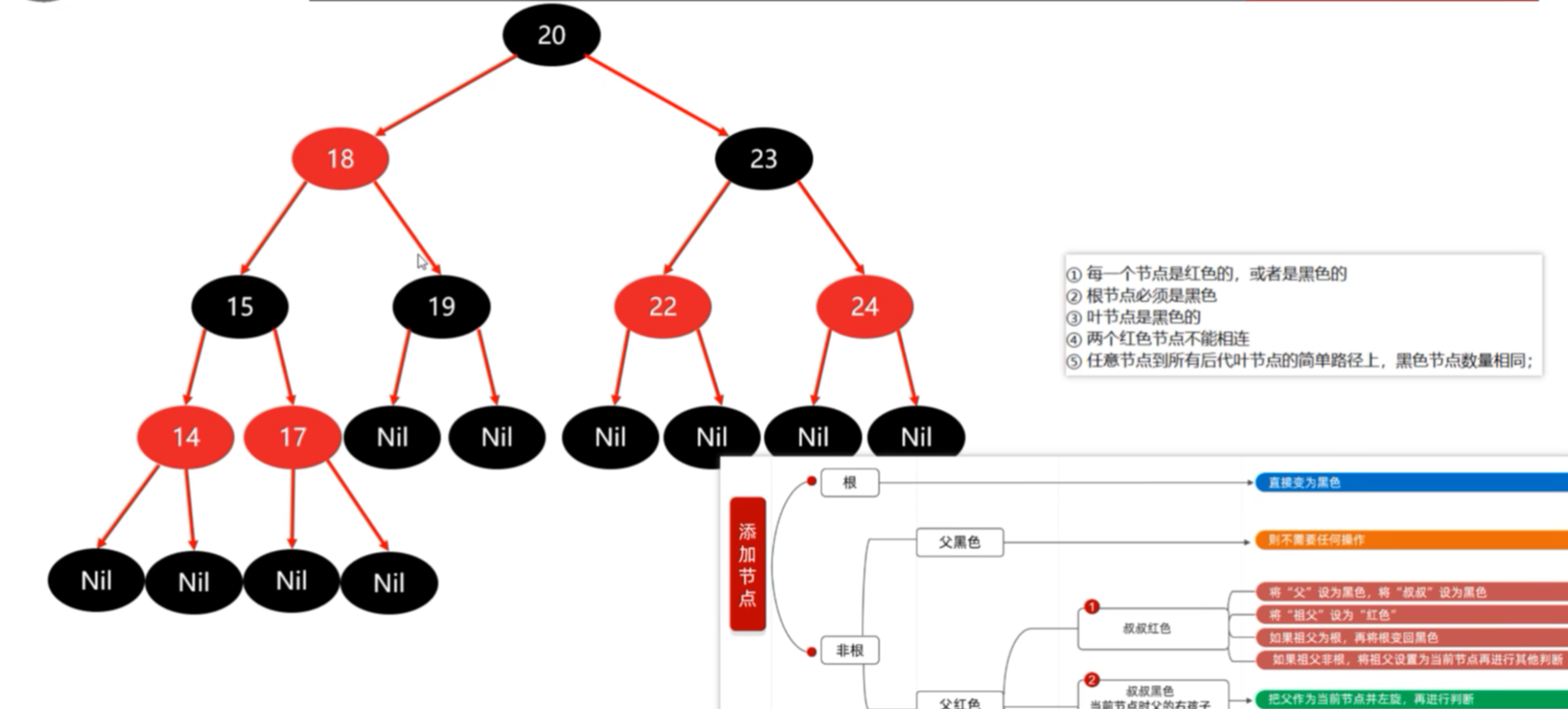
旋转时,不需要考虑叶子节点,转完之后再把叶子节点添加上即可。
1.3 红黑树 vs AVL 树对比(工程选择)
| 特性 | 红黑树 | AVL 树 |
|---|---|---|
| 平衡程度 | 近似平衡 | 严格平衡 |
| 查询时间 | O(log n) | O(log n) |
| 插入/删除 | 更快(少旋转) | 较慢(多旋转) |
| 实现复杂度 | 中等 | 较高 |
| 适用场景 | 频繁插入/删除(如 TreeMap) | 查询密集型 |
✅ Java 中的 TreeMap 和 TreeSet 使用的是红黑树
最终总结:红黑树的核心思想
红黑树的本质是“用颜色代替高度”来实现平衡
- 红色:表示“临时失衡”,可以调整
- 黑色:表示“稳定”,必须保持路径一致
- 通过变色和旋转,将局部失衡转化为全局平衡
🌟 最后一句话总结:
“红黑树就像一位聪明的舞者——它允许自己短暂‘歪斜’,但总能在下一个节拍里优雅地旋转回来,保持整体节奏的和谐!”
声明:
题目详细分析借鉴于通义AI
以上均来源于B站@ITheima的教学内容!!!
本人跟着视频内容学习,整理知识引用
