当前位置：首页 > news >正文

πRL——首个在线RL微调流式VLA π0/π0.5的框架：通过Flow-Noise和Flow-SDE实现精确对数似然估计，全面提升性能

news 2025/11/11 10:50:03

前言

由于我司过去一年一直侧重这五大场景的落地：机械臂的智能插拔与装配、人形灵巧操作、人形展厅讲解、人形搬运(含轮式和双足)、自动加油机器人

而对于其中的「机械臂智能插拔与装配」而言，如本博客之前的两篇文章所说

《知识蒸馏RLDG：先基于精密任务训练RL策略(HIL-SERL)，得到的RL数据去微调OpenVLA，最终效果超越人类演示数据》
首发于25年8月底，文中曾说：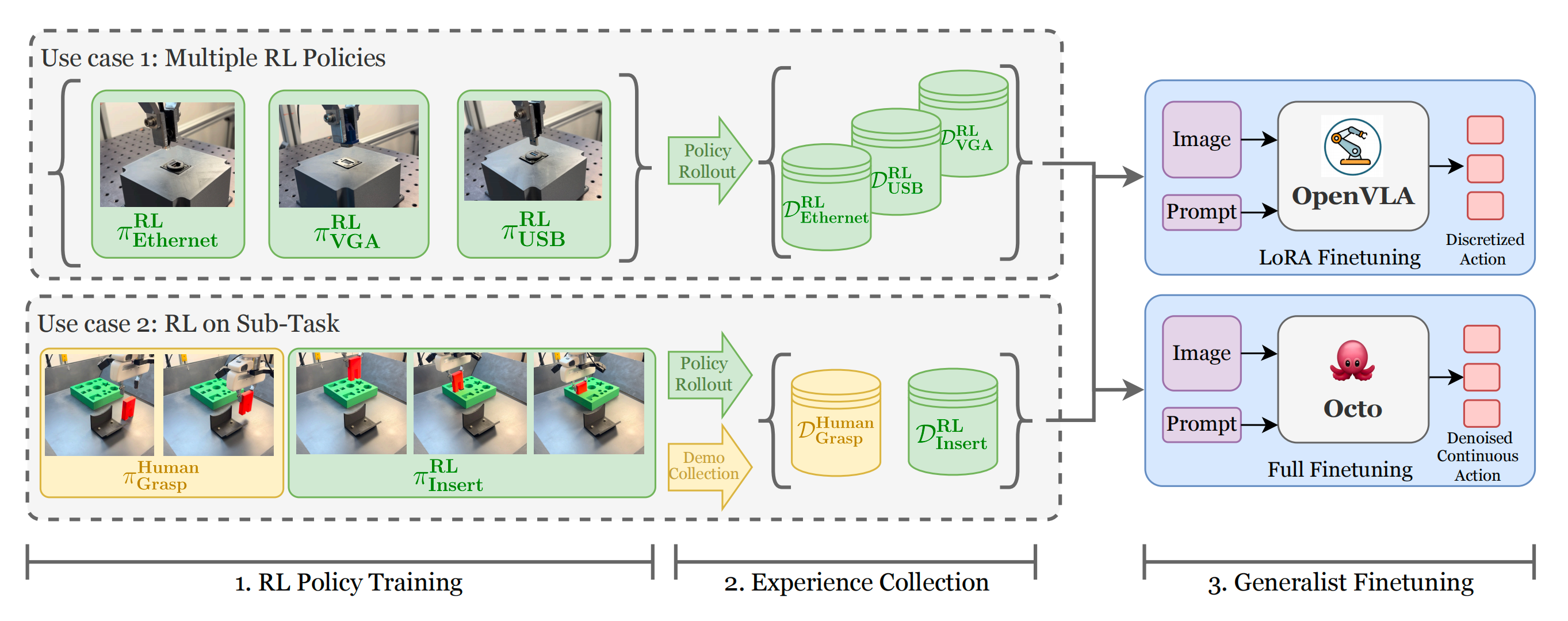
如果想兼具精准度和泛化性，RL微调vla 暂时最合适
我估计，RL结合VLA的方法，很快会成为工厂里智能机械臂的主流落地方法
《ConRFT——Consistency Policy下RL微调VLA的方法：离线通过演示数据微调(结合Q损失和BC损失)，后在线RL微调，且引入人工干预》
首发于25年9月上旬，我在该文中再次表达了类似的观点
对于工厂里机械臂的智能化改造，很显然，如果用单纯RL的话，其准度不错，但泛化性不行，如果想兼具精准度和泛化性，RL微调vla 最合适
故我相信，RL结合VLA的方法，很快会成为工厂里智能机械臂的主流落地方法

上面这两篇文章皆收录于此系列《精密插拔与装配：从RL、VLA(含力/触)到RL微调VLA》中，而通过本博客内的这个系列可知，在线RL微调自回归VLA(比如openvla)已经不新鲜了，甚至在线RL微调扩散策略也已不新鲜『比如Learning multimodal behaviors from scratch with diffusion policy gradient，及Diffusion policy policy optimization, 2024，简称DPPO』

但微调流式VLA，则相对少见，好在

25年11.5日，在我司实习的夏同学「其来自北京一985，PS，我司长沙具身总部一直在扩招985/211的硕士实习生，如可来长实习，欢迎私我」，在公司群内分享了一则视频
————
号称：【花式叠衣2.0】 VLA+RL再升级！长程、丝滑、泛化自主叠衣，想怎么叠就怎么叠
我当时回复他道：
有出来个πRL——该视频可能就类似这个模式
在线RL优化π0/π0 5，可能效果比x-vla，或π0/π0.5效果更好

本文便来解读下这个πRL：首个在线RL微调流式VLA的框架

第一部分 πRL：基于流式VLA的在线强化学习微调

1.1 引言、相关工作、背景知识

1.1.1 引言

如πRL论文所述，VLAs 的训练方法遵循如图1所示的标准预训练与有监督微调（SFT）范式

在预训练的VLM基础上，VLA 会首先在大规模、异构的人类演示数据集上进行微调
然后在目标任务上进行有监督微调（SFT），以使其能力与特定的机器人形态与环境对齐
然而，依赖SFT会带来关键挑战：
构建大规模高质量的专家轨迹既费力又昂贵(Din 等，2025)
而且通过SFT获得的模型往往会过拟合于专家演示数据(Fei 等，2025)

近期的研究工作（Zang 等，2025；Li 等，2025a；Tan 等，2025；Liu 等，2025b）已探索通过强化学习（RL）扩展 VLA 的训练过程，建立了如图1所示的预训练、SFT 及 RL 训练范式，使 VLA 能够通过主动环境交互和制定更具泛化能力的策略，将其性能提升至超越最初专家示范的水平

然而，这些强化学习的进展主要局限于自回归视觉-语言代理（VLA）领域，典型代表包括 Open-VLA、OpenVLA-OFT
它们采用离散动作解码器，以自回归或并行方式生成输出
这与基于扩散或流的 VLA 形成鲜明对比，如π 系列模型 π0和 π0.5
它们通过在流匹配(Lipman 等2022)中的迭代细化过程生成动作
这种方式不仅能以高频率产生动作块，还能完成高灵巧度的任务

因此，现有的 VLA-RL 算法无法兼容基于流的 VLA，其根本挑战在于如何针对所执行的动作刻画对数似然（Hutchinson,1989；Chen 等，2018）

对此，来自♠Tsinghua University、♣Peking University、♢Institute of Automation, Chinese Academy of Sciences(即中科院自动化所)、♯Carnegie Mellon University、♢Infinigence AI、♡Zhongguancun Academ(即中关村学院)的研究者推出了πRL，这是首个用于微调基于流的VLA(即π0和π0.5)的开源并行在线强化学习框架

其对应的paper地址为：π𝚁𝙻: Online RL Fine-tuning for Flow-based Vision-Language-Action Models
其对应的作者包括
Kang Chen♣,♡,∗、Zhihao Liu♢,♡,∗、Tonghe Zhang♯,∗、Zhen Guo♢、Si Xu♢、Hao Lin♢
Hongzhi Zang♠、Quanlu Zhang♢、Zhaofei Yu♣、Guoliang Fan♢、Tiejun Huang♣、Yu Wang♠、Chao Yu♠,♡,†
其对应的GitHub地址为：github.com/RLinf/RLinf
其对应的hf 地址为：huggingface.co/RLinf

且作者为了解决流匹配中难以处理的对数似然估计问题，他们提出了两种解决方案：

Flow-Noise
将可学习的噪声网络集成到去噪流程中，并将该阶段建模为离散时间马尔可夫决策过程（MDP），以实现精确的对数似然估计
Flow-SDE 则将普通微分方程（ODE）去噪流程转化为随机微分方程（SDE），在保证等效边缘分布用于探索的同时，构建了将去噪流程与策略—环境交互耦合的两层 MDP，并配合混合 ODE-SDE 采样技术来加速训练

在构建的 MDP 和精确对数似然计算基础上，πRL 通过近端策略优化即PPO算法进行进一步优化

1.1.2 相关工作

首先，对于VLA

VLA 模型最近通过集成多模态输入，在机器人领域取得了显著进展，实现了统一的感知、推理与控制。这一进展催生了一系列架构，包括Octo（Team 等，2024）、RT（Brohan 等，2022）、OpenVLA、OpenVLA-OFT、π0, π0.5 和GR00T（Bjorck 等，2025）

OpenVLA 作为自回归VLA 架构的代表，将动作空间离散化为符号化表示
这使得基于语言条件的控制成为可能，通过将动作作为VLM 词汇表的一部分进行处理，但该方法在本质上限制了实现精细化运动所需的分辨率
为了实现更加灵巧且连续的物理行为，π0 和π0.5 作为基于流的VLA 架构的代表，引入了基于流匹配的动作分块架构
这使VLA 能够建模复杂的连续动作分布，从而实现更为灵巧的物理行为

而本文介绍的πRL则通过在线RL算法对π系列模型进行了进一步微调，通过与环境的在线交互，提升了其性能和泛化能力

其次，对于面向VLA的在线RL微调

近期的研究越来越多地集中于利用在线RL提升VLA的性能和泛化能力。例如

SimpleVLA-RL基于OpenVLA-OFT和GRPO，展示了在数据稀缺情况下，强化学习能够提升VLA模型的长程规划能力
RL4VLA通过阶段性稀疏奖励，实证评估了PPO、GRPO和直接偏好优化（DPO）（Rafailov等，2023），发现PPO表现最佳
VLA-RL提出了专用的机器人流程奖励模型，并优化了数据处理流程
iRe-VLA提出了在强化学习探索与SFT更新之间迭代的框架
详见此文《iRe-VLA——RL微调VLA：先SFT、后在线RL，最后结合“离线演示和在线成功数据”对VLA做SFT(含GRAPE的详解)》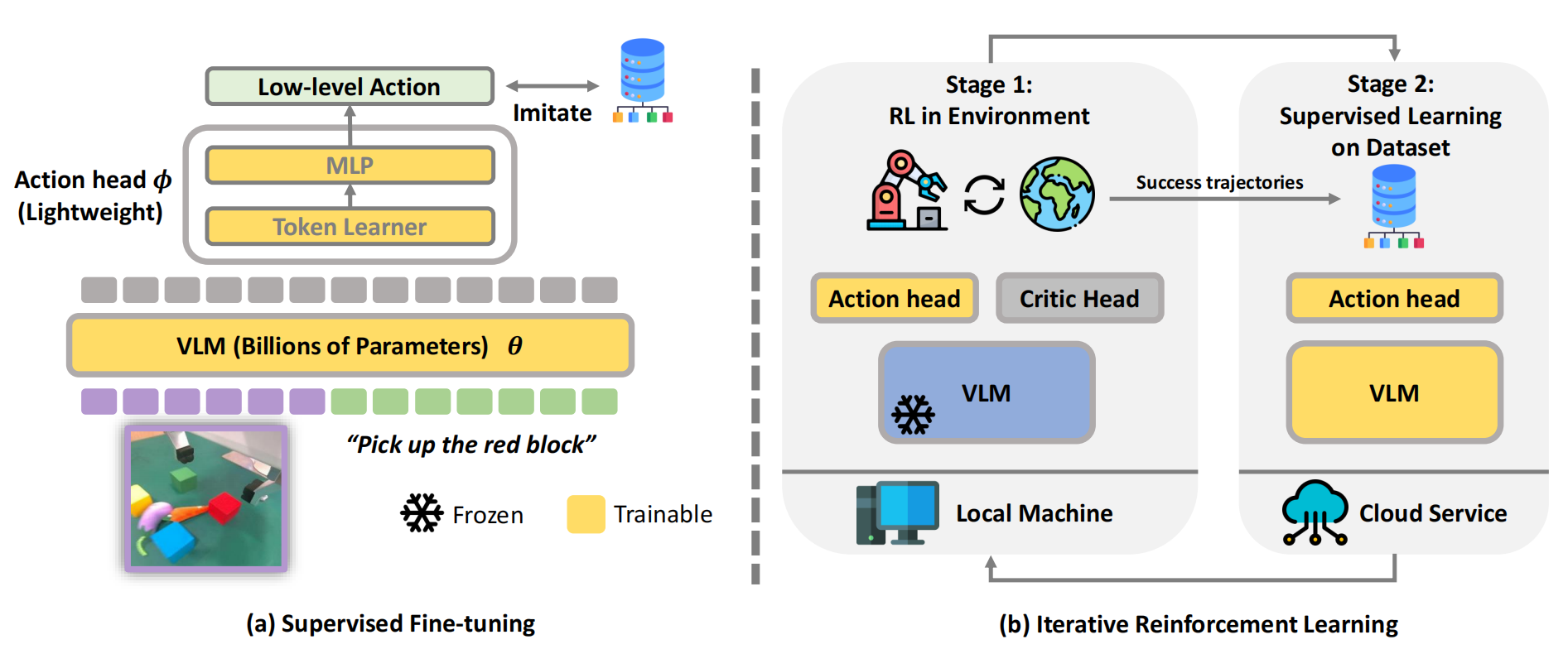
RIPT-VLA将REINFORCE leave-one-out（RLOO）（Kool等，2018）算法应用于QueST（Mete等，2024）和OpenVLA-OFT架构
RLinf-VLA为大规模强化学习训练VLA模型提供了统一且高效的框架，支持多样化的VLA——OpenVLA 和 OpenVLA-OFT 等架构，以及 PPO、GRPO 等多种强化学习（RL）算法，还有包括LIBERO 和 ManiSkill 在内的多种模拟器

总之，以上这些工作展示了强化学习微调 VLA 模型的有效性

尽管这些方法展示了将在线RL应用于VLA的潜力，但由于精确对数似然估计的挑战，它们在基于流的VLA中的应用仍受限

最后，对于用于流模型的强化学习微调

将RL与流模型结合是一种有前景的方法，可以突破模仿学习的局限性。为此

Flow-GRPO（Liu 等，2025a）将确定性常微分方程（ODE）转化为等价的随机微分方程（SDE），以实现随机性探索
在此基础上，后续研究如 Mix-GRPO（Li 等，2025b）和TempFlow-GRPO（He 等，2025）通过混合 ODE-SDE rollout 进一步加速训练
ReinFlow（Zhang 等，2025）在流路径中注入可学习的噪声，并将其转化为具有可计算似然的离散时间马尔可夫过程，从而实现稳定的策略梯度更新
——
流策略优化（FPO，McAllister 等，2025）将策略优化重构为最大化条件流匹配损失的优势加权比
此外，策略无关强化学习（PA-RL，Mark 等，2024）能够通过监督学习将评论家优化后的动作蒸馏到策略中，实现对各类扩散和 Transformer 架构的高效微调
————
通过强化学习引导扩散（DSRL，Wagenmaker 等，2025）则在其潜在噪声空间中执行强化学习，从而优化流策略，而无需直接修改策略参数本身

尽管以往的研究大多集中于非机器人任务或小规模、单一任务的机器人领域，但πRL则针对更具挑战性的难题：即对大规模基于流的VLA在复杂多任务机器人场景中的微调

1.1.3 问题表述与基于流的VLA

首先，对于问题定义

在πRL中

作者将该任务形式化为一个MDP，由元组 $\mathcal{M}=\left(\mathcal{S}, \mathcal{A}, P_{0}, P_{\mathrm{ENV}}, R_{\mathrm{ENV}}, \gamma\right)$ 定义
状态 $s_{t} \in \mathcal{S}$ 被定义为机器人观测 $\mathbf{o}_{t}$ ， $P_{0}$ 表示初始状态分布
给定状态，流式策略预测动作 $a_{t} \sim \pi\left(\cdot \mid s_{t}\right) \in \mathcal{A}$ ，从而产生状态转移 $s_{t+1} \sim P_{\text {ENV }}\left(\cdot \mid s_{t}, a_{t}\right)$ ，并获得奖励 $P_{\mathrm{ENV}}\left(\cdot \mid s_{t}, a_{t}\right)$
目标是学习一个策略 $\pi_{\theta}$ ，使其在 $T + 1$ 步时间范围内最大化期望的 $\gamma$ 折扣回报： $\mathcal{J}\left(\pi_{\theta}\right)=\mathbb{E}_{\pi_{\theta}, P_{0}}\left[\sum_{t=0}^{T} \gamma^{t} R_{\mathrm{ENV}}\left(s_{t}, a_{t}\right)\right]$

通过策略梯度代理，回报期望的梯度可以根据采样得到的轨迹进行近似(定义为公式2)
$\nabla_{\theta} \mathcal{J}\left(\pi_{\theta}\right)=\mathbb{E}_{\pi_{\theta}, P_{0}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) A\left(s_{t}, a_{t}\right)\right]$
其中的优势函数 $A\left(s_{t}, a_{t}\right)=Q\left(s_{t}, a_{t}\right)-V\left(s_{t}\right)$ ，衡量动作价值Q (st, at) 相对于状态价值V (st)的相对优劣，为策略更新提供了低方差的信号

其次，对于基于流的VLA而言，π0 被设计用于将由RGB 图像、语言token和机器人本体感觉组成的观测 $\mathbf{o}_{t}$ 映射为未来H 步动作序列 $\mathbf{A}_{t}=\left[a_{t, 0}, \ldots, a_{t, H-1}\right]$ ，其形式化为 $p\left(\mathbf{A}_{t} \mid \mathbf{o}_{t}\right)$

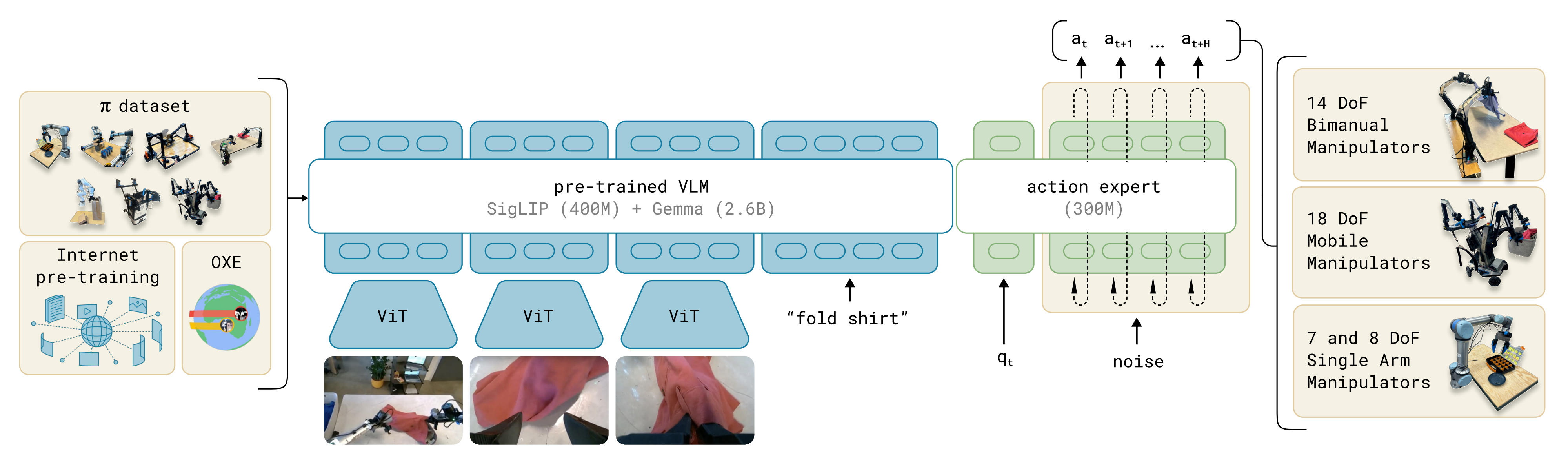
在该模型中，VLM 从视觉和语言输入中提取特征，而流匹配专家负责生成动作
具体而言，该模型学习一个条件向量场 $\mathbf{v}_{\theta}$ ，用于将标准高斯噪声分布变换为目标动作 $\mathbf{A}_{t}$
这是通过最小化条件流匹配CFM损失来实现的，该损失将预测的向量场 $\mathbf{v}_{\theta}$ (说白了，就是预测的噪声)，与真实向量场 $\mathbf{u}$ (说白了，就是真实添加的噪声) 对齐
$\mathcal{L}_{\mathrm{CFM}}=\mathbb{E}_{\tau, p\left(\mathbf{A}_{t}, \mathbf{o}_{t}\right), q\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)}\left[\left\|\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right)-\mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)\right\|_{2}^{2}\right]$
————
我们已知以下内容：通过给一个纯净动作 $\mathbf{A}_{t}$ 不断一点一点加噪 $\mathbf{u}$ 从而一点一点变成 $\mathbf{A}_{t}^{\tau}$ 『 $\mathbf{A}_{t}^{\tau}$ 包含两个时间指标，t 表示环境交互中的离散时间步，τ 表示流匹配中的连续时间变量』，最终得到一个完全噪声 $\epsilon$
换言之，条件概率路径 $q\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)$ 从动作 $\mathbf{A}_{t}$ 生成一个带噪动作 $\mathbf{A}_{t}^{\tau}=\tau \mathbf{A}_{t}+(1-\tau) \epsilon$ ，其中随机噪声 $\epsilon \sim \mathcal{N}(0, I)$ ，连续时间 $\tau \in[0,1]$ 用于流匹配
对于这个特定路径，对应的真实向量场被定义为 $\mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)=\epsilon-\mathbf{A}_{t}$

注意，原论文『我于25年11.10首发的本文，看的πRL论文当时的版本是Submitted on 29 Oct 2025』这里写的 $\mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)=\mathbf{A}_{t}-\epsilon$ 是个笔误

正确的应该如π0论文中所说：training the network outputs vθ (Aτt , ot) to match the denoising vector field u(Aτt |At) = ϵ −At 』
得到了所添加的真实噪声 $\mathbf{u}$ 之后(通过 $\mathbf{v}_{\theta}$ 来预测)，便可以通过该公式 $\mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)=\epsilon-\mathbf{A}_{t}$ ，计算得到纯净动作： $\mathbf{A}_{t} =\epsilon - \mathbf{u}\left(\mathbf{A}_{t}^{\tau} \mid \mathbf{A}_{t}\right)$

在推理过程中，动作序列首先通过对噪声向量 $\mathbf{A}_{t}^{0} \sim \mathcal{N}(0, I)$ 进行采样生成，之后再通过基于前向欧拉方法，将学习到的向量场 $\mathbf{v}_{\theta}$ 在固定步数内迭代地集成，不断细化： $\mathbf{A}_{t}^{\tau+\delta}=\mathbf{A}_{t}^{\tau}+\mathbf{v}_{\theta}\left(\mathbf{A}_{t}^{\tau}, \mathbf{o}_{t}\right) \cdot \delta .$

1.2 πRL提出的两种方法：Flow-Noise 和Flow-SDE

现有的 VLA-RL 方法分别利用 OpenVLA 这类基础模型用于离散动作，使用 OpenVLA-OFT 进行连续动作

为计算动作对数似然 $\log \pi_{\theta}\left(a_{t} \mid s_{t}\right)$

离散模型（Liu 等，2025b）对输出 logits 应用 softmax
而连续模型（Li 等，2025a）则将动作视为高斯分布，并使用预测头来估计方差

对于基于流的 VLA，若直接计算精确的似然（Hutchinson，1989），在去噪步骤较少时准确性较差。此外，其常微分方程采样过程是确定性的，缺乏探索性，使其在强化学习中的实现较为复杂

对此，作者提出了 Flow-Noise 和Flow-SDE 两种技术方法，使基于流的 VLA 更适用于强化学习，如图 2 所示

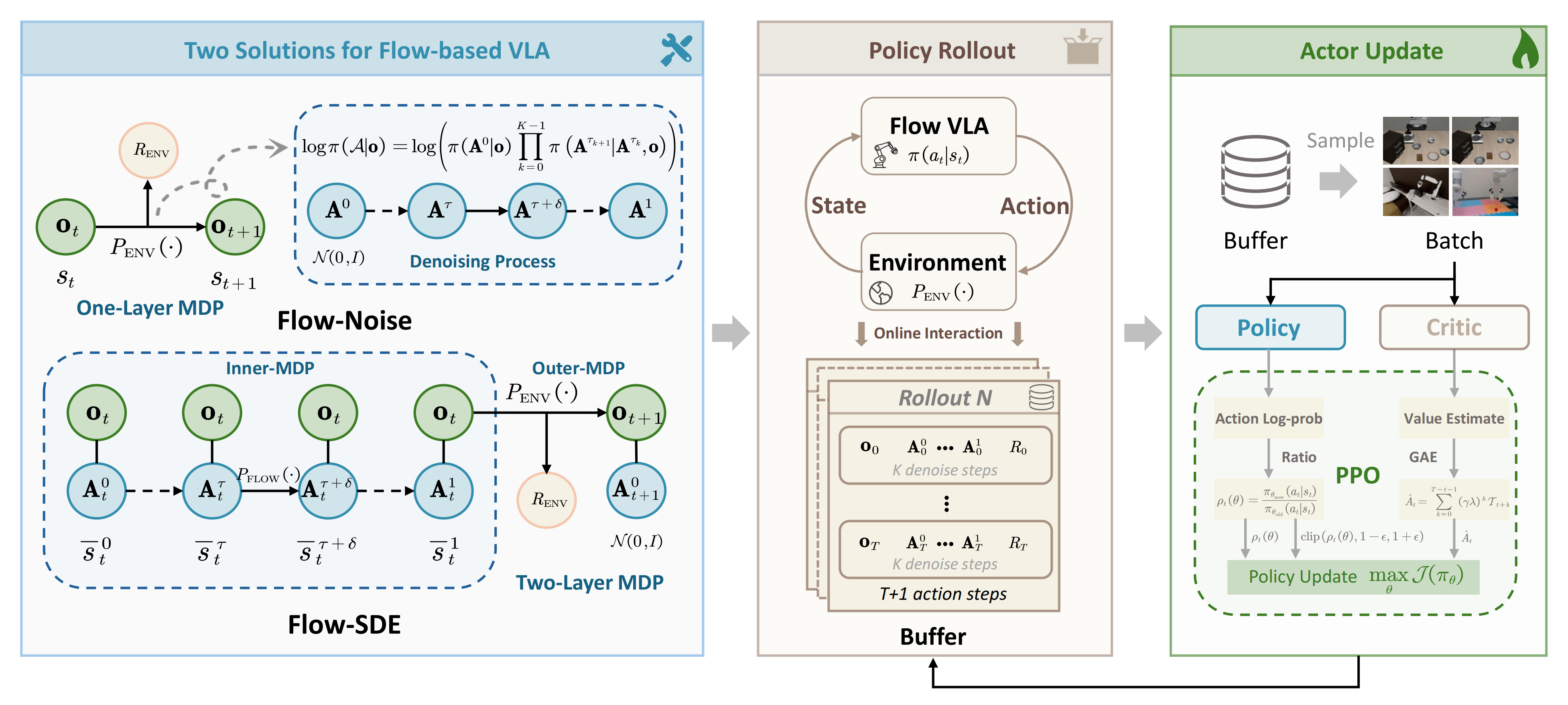
1.2.1 Flow-Noise(流噪声）：包含随机性注入和对数似然估计

受 Reinflow『即Reinflow: Fine-tuning flow matching policy with online reinforcement learning』的启发

如Reinflow论文所说，精化随机策略对于连续控制问题至关重要 [49]

然而，对于条件流来说，其样本路径由神经常微分方程（ODE）控制，连对数概率这一衡量随机性的关键因素都可能难以获得，并且在反向传播过程中不稳定。这一问题在只用极少去噪步数推断流策略时更加严重，因为此时离散化误差会变大，但推断成本却较低
其次，与离线强化学习方法相比，在线强化学习微调要求策略在探索与利用之间进行权衡，尤其是在稀疏奖励环境下 [20]
然而，对于具有确定性路径的条件流，如何设计合理的探索机制仍然尚未解决

对此，他们提出了ReinFlow，这是第一个能够稳定地在线微调一类流匹配策略的强化学习算法，尤其能够在很少甚至仅一次去噪步骤中实现

Reinflow的作者训练了一个噪声注入网络，将流转换为具有高斯转移概率的离散时间马尔可夫过程，从而实现精确且易于计算的似然度
且设计允许噪声网络自动平衡探索与利用
即该方法实现轻便，内建探索机制，并能广泛适用于各类流策略变体，包括基于Rectified Flow [34]和Shortcut Models [18]参数化的模型

作者在流匹配去噪过程中引入了可学习的噪声网络，并在上文1.3.1节中详述的标准单层 MDP 框架下解决该问题

通过将去噪阶段建模为一个离散MDP，作者可以直接计算去噪序列的对数似然，从而能够通过强化学习实现等价的策略优化

1.2.1.1 随机性注入

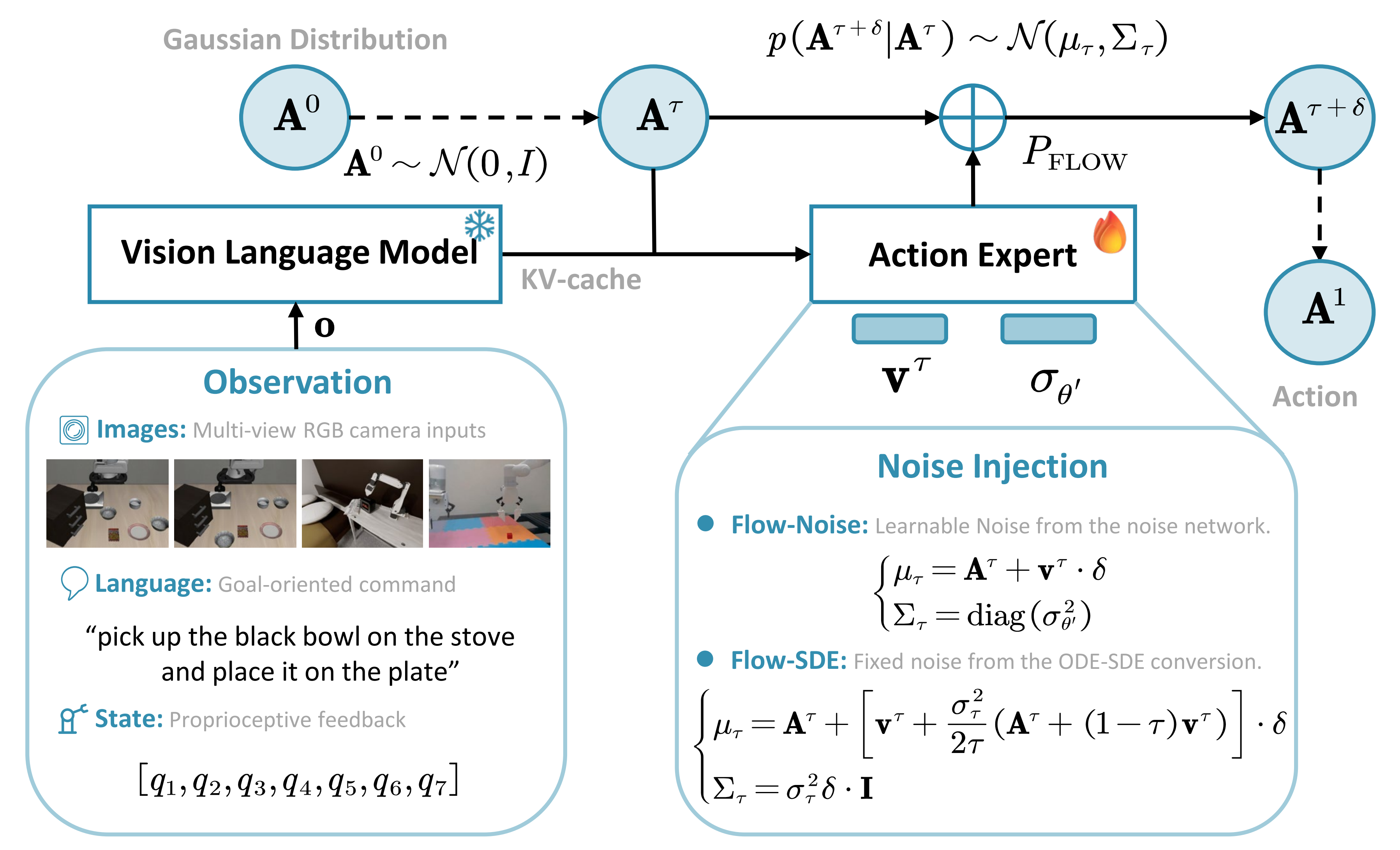
在Flow-Noise 中，作者用神经网络对噪声调度进行参数化，使注入噪声的幅度能够在训练过程中动态学习，从而具有更大的灵活性，如图3 所示『注意， $\mathcal{A}=\left(\mathbf{A}^{0}, \ldots, \mathbf{A}^{1}\right)$ 是一个去噪序列』

上图是展示在流匹配过程中噪声注入的示意图，以π0.5为例，它融合了图像、语言和状态信息，实现了统一的VLM输入
作者关注于单个环境时间步t 内的生成过程
为了符号简洁，省略时间下标t，例如，将 $\mathbf{A}_{t}^{\tau}$ 写作 $\mathbf{A}^{\tau}$ ，并将预测速度 $\mathbf{v}_{\theta}\left(\mathbf{A}^{\tau}, \mathbf{o}\right)$ 记作 $\mathbf{v}^{\tau}$

在去噪过程中，步进转移被建模为各向同性高斯分布 $p\left(\mathbf{A}^{\tau+\delta} \mid \mathbf{A}^{\tau}\right) \sim \mathcal{N}\left(\mu_{\tau}, \Sigma_{\tau}\right)$ ，其中均值由原始常微分方程的前向欧拉更新决定，方差则由可学习的噪声网络 $\theta^{\prime}$ 控制

$\left\{\begin{array}{l} \mu_{\tau}=\mathbf{A}^{\tau}+\mathbf{v}^{\tau} \cdot \delta \\ \Sigma_{\tau}=\operatorname{diag}\left(\sigma_{\theta^{\prime}}^{2}\right) \end{array}\right.$

这里， $\sigma_{\theta^{\prime}}(\cdot)$ 是从噪声注入网络中学习得到的标准差，该网络以动作 $\mathbf{A}^{\tau}$ 和观测 $\mathbf{o}$ 为条件。噪声网络与velocity网络联合训练，但在微调后被弃用，此时用于推理的策略为确定性策略

1.2.1.2 对数似然估计

在将策略梯度方法应用于基于流的VLA时，主要挑战来自于最终执行动作的对数似然不可求解

而在Flow-Noise中，作者通过将整个去噪过程的联合对数似然的梯度替代到等式(2)的策略优化目标中

$\nabla_{\theta} \mathcal{J}\left(\pi_{\theta}\right)=\mathbb{E}_{\pi_{\theta}, P_{0}}\left[\sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}\left(a_{t} \mid s_{t}\right) A\left(s_{t}, a_{t}\right)\right]$

从而解决了这一问题，而这一做法在理论上受到了Reinflow的支持

动作生成的推理过程被离散化为 $K$ 个均匀的步骤，这定义了一系列时间点 $\left\{\tau_{0}, \tau_{1}, \ldots, \tau_{K}\right\}$ 。步长被定义为 $\delta=1 / K$ ，在第 $k$ 个时间点的离散时间步为 $\tau_{k}=k \cdot \delta$ ，从 $\tau_{0}=0$ 开始，到 $\tau_{K}=1$ 结束
给定观测 $\mathbf{o}$ ，整个去噪序列 $\mathcal{A}=\left(\mathbf{A}^{0}, \ldots, \mathbf{A}^{1}\right)$ 的精确且易处理的对数概率如图2 所示
并表述为
$\log \pi(\mathcal{A} \mid \mathbf{o})=\log \left(\pi\left(\mathbf{A}^{0} \mid \mathbf{o}\right) \prod_{k=0}^{K-1} \pi\left(\mathbf{A}^{\tau_{k+1}} \mid \mathbf{A}^{\tau_{k}}, \mathbf{o}\right)\right)$

在此基础上，可以在标准的马尔可夫决策过程（MDP）框架内处理基于流的方法策略优化

1.2.2 FLOW-SDE(流-随机微分方程)：随机性注入、MDP建模、HYBRIDODE-SDE采样

受到 Flow-GRPO的启发，作者通过将去噪过程从 ODE 转化为 SDE 形式来增强随机探索能力。且进一步构建了两层 MDP，将去噪过程与基于 DPPO（Ren等，2024）的策略-环境交互耦合，同时利用混合 ODE-SDE 采样技术加速训练过程

1.2.2.1 随机性注入

在 Flow-SDE 中，作者将确定性常微分方程（ODE）转化为等效的随机微分方程（SDE），以保留生成动作的边缘概率密度，如图3所示

流匹配的确定性常微分方程采样轨迹，特别是Rectified Flow（Liu等人，2022），通过前向欧拉方法进行描述(定义为公式6)：

$d \mathbf{A}^{\tau}=\mathbf{v}^{\tau} d \tau$

基于概率流ODE与SDE之间的联系，作者可以将公式6中的确定性ODE转化为等效的SDE，其中漂移项(drift term)修正了原始速度，而扩散项(diffusion term)引入了噪声(定义为公式7)

$d \mathbf{A}^{\tau}=\underbrace{\left(\mathbf{v}^{\tau}-\frac{1}{2} g^{2}(\tau) \nabla \log q_{\tau}\left(\mathbf{A}^{\tau}\right)\right) d \tau}_{\text {Drift Term }}+\underbrace{g(\tau) d \mathbf{w}}_{\text {Diffusion Term }}$

其中

$g(\tau)$ 是控制噪声进度的标量函数
$\nabla \log q_{\tau}\left(\mathbf{A}^{\tau}\right)$ 是边缘分布 $q_{\tau}$ 的得分函数
$d \mathbf{w}$ 表示一个Wiener 过程

如在Flow-GRPO 中所建立，分数函数score function和速度场(velocity field) $\mathbf{v}^{\tau}$ 通过 $\nabla \log q_{\tau}\left(\mathbf{A}^{\tau}\right)=-\frac{\mathbf{A}^{\tau}}{\tau}-\frac{1-\tau}{\tau} \mathbf{v}^{\tau}$ 密切相关

通过在公式(7) 中用速度场(velocity field) $\mathbf{v}^{\tau}$ 替换分数函数，并将噪声调度 $g(\tau)$ 设为 $\sigma_{\tau}=a \sqrt{\frac{\tau}{1-\tau}}$ ，其中 $a$ 控制噪声水平，则得到了用于flow-matching 采样器的最终SDE 公式

$d \mathbf{A}^{\tau}=\left[\mathbf{v}^{\tau}+\frac{\sigma_{\tau}^{2}}{2 \tau}\left(\mathbf{A}^{\tau}+(1-\tau) \mathbf{v}^{\tau}\right)\right] d \tau+\sigma_{\tau} d \mathbf{w}_{\tau}$

对该SDE 进行离散化可以看出，转移概率 $p\left(\mathbf{A}^{\tau+\delta} \mid \mathbf{A}^{\tau}\right) \sim \mathcal{N}\left(\mu_{\tau}, \Sigma_{\tau}\right)$ 是一个各向同性高斯分布，其均值和方差表达如下：

$\left\{\begin{array}{l} \mu_{\tau}=\mathbf{A}^{\tau}+\left[\mathbf{v}^{\tau}+\frac{\sigma_{\tau}^{2}}{2 \tau}\left(\mathbf{A}^{\tau}+(1-\tau) \mathbf{v}^{\tau}\right)\right] \cdot \delta \\ \Sigma_{\tau}=\sigma_{\tau}^{2} \delta \cdot \mathbf{I} \end{array}\right.$

1.2.2.2 MDP建模

虽然Flow-Noise 用整个去噪序列的联合对数似然替代了最终执行动作的似然，但作者在Flow-SDE 中将流匹配的去噪过程与环境交互结合起来

具体而言，作者将去噪过程中定义的内部MDP 嵌入到上文中所述的高层外循环MDP 以及环境MENV 中，形成如图2所示的两层MDP

其中各组成部分以环境时间 $t$ 和去噪时间 $\tau$ 来定义

状态 $\bar{s}_{t}^{\tau}=\left(\mathbf{o}_{t}, \mathbf{A}_{t}^{\tau}\right)$ 是由观测 $\mathbf{o}_{t}$ 和动作状态 $\mathbf{A}_{t}^{\tau}$ 组成的元组
动作 $\bar{a}_{t}^{\tau}$ 定义为内循环中下一个采样的去噪动作，以及外循环中执行的动作(定义为公式10)
$\bar{a}_{t}^{\tau}=\left\{\begin{array}{ll} \mathbf{A}_{t}^{\tau+\delta} & \text { if } \tau<1 \\ \mathbf{A}_{t}^{1} & \text { if } \tau=1 \end{array}\right.$
其中， $\mathbf{A}_{t}^{\tau+\delta}=\mu_{\tau}+\sigma_{\tau} \sqrt{\delta} \cdot \boldsymbol{\epsilon}, \boldsymbol{\epsilon} \sim \mathcal{N}(0, \mathbf{I})$ 是随机采样的噪声
转移 $\bar{P}\left(\bar{s}_{t^{\prime}}^{\tau^{\prime}} \mid \bar{s}_{t}^{\tau}, \bar{a}_{t}^{\tau}\right)$ 定义了状态的演化方式，表述如下
$\bar{s}_{t^{\prime}}^{\tau^{\prime}}=\left\{\begin{array}{ll} \left(\mathbf{o}_{t}, \bar{a}_{t}^{\tau}\right) & \text { if } \tau<1 \\ \left(\mathbf{o}_{t+1}, \mathbf{A}_{t+1}^{0}\right) & \text { if } \tau=1 \end{array}\right.$
————
$\rightarrow$ 对于 $\tau<1$ ，内循环 inner loop转移 $P_{\text {FLOW }}(\cdot)$ 发生在不同去噪动作状态之间，此时观测值 $\mathbf{o}_{t}$ 保持不变，下一步的动作状态由 $\bar{a}_{t}^{\tau}=\mathbf{A}_{t}^{\tau+\delta}$ 设定
$\rightarrow$ 对于 $\tau=1$ ，最终动作 $\bar{a}_{t}^{\tau}=\mathbf{A}_{t}^{1}$ 与外循环outer-loop环境交互，根据环境动力学 $P_{\mathrm{ENV}}(\cdot)$ 产生新的观测值 $\mathbf{o}_{t+1}$ 。同时，动作状态从标准正态分布 $\mathbf{A}_{t+1}^{0} \sim \mathcal{N}(0, I)$ 重新初始化
奖励 $\bar{R}\left(\bar{s}_{t}^{\tau}, \bar{a}_{t}^{\tau}\right)$ 仅在去噪过程完成并与环境交互后才会发放如下所示
$\bar{R}\left(\bar{s}_{t}^{\tau}, \bar{a}_{t}^{\tau}\right)=\left\{\begin{array}{ll} 0 & \text { if } \tau<1 \\ R_{\mathrm{ENV}}\left(\mathbf{o}_{t}, \mathbf{A}_{t}^{1}\right) & \text { if } \tau=1 \end{array}\right.$

在两层MDP 框架内，估计动作对数似然 $\log \pi\left(a_{t} \mid s_{t}\right)$ 的问题被转化为估计 $\log \pi\left(\bar{a}_{t}^{\tau} \mid \bar{s}_{t}^{\tau}\right)$ ，由于转移的高斯性质，该估计可以直接计算

1.2.2.3 HYBRIDODE-SDE 采样：降低训练难度与所需的计算时间

在所提出的两层MDP框架中，有效轨迹长度等于环境交互步骤数与流匹配去噪步骤数的乘积。虽然这种建模方式使基于流的VLA能够进行强化学习训练，但其MDP时域长度相比非迭代式VLA方法大大延长，因此显著增加了训练的难度以及优化所需的计算时间

为此，作者采用了混合ODE-SDE 展开策略，灵感来源于文本到图像生成方法，如Mix-GRPO（Li 等，2025b）和TempFlow-GRPO（He 等，2025）
————
具体而言，在去噪过程中，会随机选择一步作为由 $p\left(\mathbf{A}^{\tau+\delta} \mid \mathbf{A}^{\tau}\right) \sim \mathcal{N}\left(\mu_{\tau}, \Sigma_{\tau}\right)$ 控制的随机SDE 转移，而其余步骤则遵循由更新规则 $\mathbf{A}^{\tau+\delta}=\mathbf{A}^{\tau}+\mathbf{v}^{\tau} \cdot \delta$ 定义的确定性ODE 转移
在这种表述下，作者将状态之间的确定性ODE 转移视为环境级封装器，并修正了先前两层MDP 的状态转移函数
————
具体来说，在每个环境步t，会随机选择一个去噪时间τt 用于策略的随机注入
$\rightarrow$ 策略π 作用于该状态 $\bar{s}_{t}^{\tau_{t}}=\left(\mathbf{o}_{t}, \mathbf{A}_{t}^{\tau_{t}}\right)$ ，根据公式(10) 采样动作 $\mathbf{A}_{t}^{\tau_{t}+\delta}$
$\rightarrow$ 环境封装器随后执行所有后续的确定性步骤，最终在新采样的时间 $\tau_{t+1}$ 时转移到下一个观测 $\mathbf{o}_{t+1}$ 和下一个动作状态 $\bar{s}_{t+1}^{\tau_{t+1}}=\left(\mathbf{o}_{t+1}, \mathbf{A}_{t+1}^{\tau_{t+1}}\right)$

在此过程中，策略的状态输入和动作输出与之前的两层MDP 表述保持一致，从而确保了理论上的一致性