图——关键路径
关键路径
文章目录
- 关键路径
- 一、前言
- 二、关键路径
- 2.1 导入
- 2.2 关键路径
- 2.2.1 定义
- 2.2.2 过程
- 2.2.3 关键路径的口算法
- 2.2.4 核心概念
- 2.2.5 代码
- 2.2.6 优缺点辨析
- 2.2.7 应用
- 三、小结
一、前言
学过了拓扑排序,有了它,可以进行任务调度,但是它有一个缺点,就是无法达到量化,不能明确具体的数据(比如:最短时间之类)。而,这是可以解决的,当我们给有向无环图加上权值,当真正的数据可以显现,这就有了关键路径,使得任务调度有了量化的数据,这大大提高了项目的效率。
接下来,我们就一起走进图的最后一个算法:关键路径~
二、关键路径
2.1 导入
关键路径的物理模型依然是有向无环图。
试想一下,如果形成了环路,那么要先做哪个事件,那就会陷入死循环,无法确定。
2.1.1 A O E AOE AOE网
A c t i v i t y Activity Activity O n On On E d g e Edge Edge,表示活动在边上的网。
顶点表示事件,边表示活动(任务),边上的权值表示完成该活动(推动一个事件到另一个事件)所需的时间。
顶点:每一个事件表示在它之前的活动已经完成(结束),在它之后的活动可以开始(像一个沟通站/中介),事件就是表示这个事实。
2.2.2 A O E AOE AOE网的源点和汇点
- 源点:起点,入度为0的点
- 汇点:汇在一起的点
关键路径和最小生成树和最短路径无关。反倒是和关注哪个路径最长。(这是时间的底线)
先解决困难问题,这个问题不能再出问题了,否则就会一拖再拖。
如图:
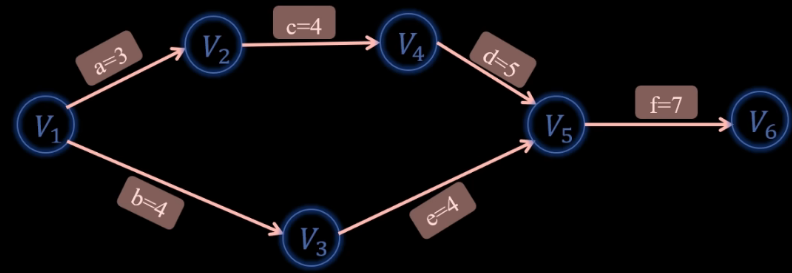
这就是 A O E AOE AOE网,其中,源点是 V 1 V1 V1,汇点是 V 6 V6 V6。
2.2 关键路径
2.2.1 定义
描述边的集合(有顺序)
拓扑排序:有顺序的顶点
这个边的顺序该怎么找呢?
在关键路径中最核心的一个问题是:完成整个工程至少需要花费多少时间
把所有边都加起来吗?肯定不对。举个例子两个人一起做一个项目,两个人分活,其中一个人花了5天做完了,另外一个人花了10天。最后项目花了多少时间呢?那很清楚了——10天。因此在一个项目中,很多活动是一起开工的,但最终的时间取决于最长的天数——最耗时的路径。
在关键路径中,其关注的是最长路径。
一个活动,最关注的是它的时间长短,但往往事件发展就取决于最长的时间,这是底线。
2.2.2 过程
一个路径,肯定有起点和终点。
起点:就是上文提到的源点,入度为0的点
终点:就是上文提到的汇点,出度为0的点
如图:
起点是 V 1 V1 V1,终点是 V 6 V6 V6
这个地方和拓扑排序很像。因此在表示关键路径之前,先确定拓扑排序,才可以找到合理的那条边。
2.2.3 关键路径的口算法
先声明一下,这个地方适合做选择判断之类题目(快速秒杀),但真正核心在于后面代码逻辑的分析。
如图:

从 V 1 V1 V1出发,有三条路径,可以到达3个点,到 V 1 V1 V1花费时间最多,先走 V 1 V1 V1。
之后是必走 V 4 V4 V4。从 V 0 V0 V0可以有两条路,但是显然,通过 V 1 V1 V1到 V 4 V4 V4花费时间最多(6 + 1 > 4 + 1)。
还有一条忽略的支路: V 0 − V 3 − V 5 V0-V3-V5 V0−V3−V5,这个过程同样是7。但是到了 V 7 V7 V7,这条路径反而不如上面的路径(长)。因此这条路径省略。
从 V 4 V4 V4到 V 7 V7 V7,有人问,为什么不走 V 6 V6 V6呢?这个明显更长啊(9 > 7),且请继续看下去。
V 4 − V 7 − V 8 V4-V7-V8 V4−V7−V8和 V 4 − V 6 − V 8 V4-V6-V8 V4−V6−V8是同样长的诶~
因此最终确定的关键路径为:
那具体该如何做呢(算法角度)?下面将迎来关键部分:代码的逻辑推导
首先呢?先做个“铺垫”。在书写代码之前,要先明白几个相关的概念。
2.2.4 核心概念
-
E T V ETV ETV
E a r l i e s t Earliest Earliest T i m e Time Time O f Of Of V e r t e x Vertex Vertex。事件(顶点)发生的最早时间。
-
L T V LTV LTV
L a t e s t Latest Latest T i m e Time Time O f Of Of V e r t e x Vertex Vertex。事件最晚发生事件。
这里的 V V V,就是关键事件。关键事件需要依靠关键路径来推导。
-
E T E ETE ETE
E a r l i e s t Earliest Earliest T i m e Time Time O f Of Of E d g e Edge Edge。活动的最早开工时间。
-
L T E LTE LTE
L a t e s t Latest Latest T i m e Time Time O f Of Of E d g e Edge Edge。活动的最晚开工时间。一个活动开始的时间是可以等的(只要在不耽误总工期的情况下)
2.2.5 代码
代码如何实现呢?
-
关于图的存储结构,因为是带权有向图,依旧是邻接表。关于接口邻接表详情,见邻接表概述。此处不再展开。
-
首先定义几个空间—— E T V ETV ETV 和 L T V LTV LTV,空间在堆上申请,因为不知道顶点具体个数。
怎么求关键路径呢?先从顶点(事件)入手,再求边。
-
拓扑排序——确定顶点的顺序
顶点的顺序就是根据拓扑排序来的
-
根据顶点顺序(拓扑排序的结果)和权值更新 E T V ETV ETV 和 L T V LTV LTV
误区:一个事件发生是看所有的入度,所有条件满足才可以发生,不是经过就可以发生
先是最早发生时间,最晚不确定,需要等到所有事件的最早时间确定下来,才可以确定最晚时间。
最晚时间的确定是倒着往回推的,一个顶点的最晚时间是看后面顶点的最早时间减去所有到达路径得到的最小值。比如:
图
这里 V 6 V6 V6是终点,如何确定 V 4 V4 V4呢?从 V 6 V6 V6回,有两条路径,最终结果应为
12 - 4 = 8,如果是12 - 2 = 10的话,从 V 4 V4 V4到 V 6 V6 V6需要4天,那么 V 6 V6 V6的最终就需要14天,会延期。这里是采用逆拓扑排序进行求得。
即从出度为0的点开始排序。
-
根据 E T V ETV ETV 和 L T V LTV LTV 计算 E T E ETE ETE 和 L T E LTE LTE,确定关键路径。
活动是事件发生的动力。
E T E ETE ETE:活动的最早发生时间等同于活动前面的事件(发出点)的最早发生时间( E T V ETV ETV)。
L T E LTE LTE:最晚时间根据LTV(该边指向的顶点的最晚开始时间) - 权值。
// 先得到拓扑排序的结构,其目的是更新ETV和LTV
static int topologicalOrder(const AGraph *graph, int *ETV, int *LTV)
{int *inDegree = malloc(sizeof(int) * graph->nodeNum); // 入度记录表if(inDegree == NULL){return -1;}memset(inDegree, 0, sizeof(int) * graph->nodeNum);// 1. 初始化图中所有顶点的入度记录表for(int i = 0; i < graph->nodeNum; i++){if(graph->nodes[i].firstEdge){ArcEdge *edge = graph->nodes[i].firstEdge;while(edge){++inDegree[edge->no];edge = edge->next;}}}// 2. 将入度为0的节点入栈,出栈的时候int top = -1;int *stack = malloc(sizeof(int) * graph->nodeNum);if(stack == NULL){free(inDegree);return -1;}// ding'y存储拓扑排序的结果空间int *topOut = malloc(sizeof(int) * graph->nodeNum);if(topOut == NULL){free(stack);free(inDegree);return -1;}// 2.1 将初始化的入度为0的顶点编号压入栈,此点就是源点for(int i = 0; i < graph->nodeNum; ++i){if(inDegree[i] == 0){stack[++top] = i;break; // 关键路径默认只有一个源点}}// 2.2 不断地弹栈,更新入度记录表int tmp = 0; // 从栈上弹出的顶点编号int index = 0; // 记录排序结果的情况while(top != -1){tmp = stack[top--]; // 出栈topOut[index++] = tmp; // 出栈的结果放到结果空间ArcEdge *edge = graph->nodes[tmp].firstEdge;// 遍历节点的出度while(edge){--inDegree[edge->no];if(inDegree[edge->no] == 0){stack[++top] = edge->no;}// 更新ETVif(ETV[tmp] + edge->weight > ETV[edge->no]){ETV[edge->no] = ETV[tmp] + edge->weight;}edge = edge->next;}}free(inDegree);free(stack);if(index < graph->nodeNum) // 有环{free(topOut);return -1;}tmp = topOut[--index];// 3.更新LTVfor(int i = 0; i < graph->nodeNum; ++i){LTV[i] = topOut[tmp];}while(index){int getTopNo = topOut[--index];ArcEdge *edge = graph->nodes[getTopNo].firstEdge;while(edge){if(LTV[edge->no] - edge->weight < LTV[getTopNo]){LTV[getTopNo] = LTV[edge->no] - edge->weight;}edge = edge->next;}}free(topOut);return 0;
}static void showTable(int *table, int n, const chae *name)
{printf("%s", name);for(int i = 0; i < n; ++i){printf(" %d", table[i]);}printf("\n");
}void keyPath(const AGraph *graph)
{// 1. 计算顶点的ETV和LTV// 申请int *ETV = malloc(sizeof(int) * graph->nodeNum);if(ETV == NULL){return;}int *LTV = malloc(sizeof(int) * graph->nodeNum);if(LTV == NULL){free(ETV);return;}// 空间初始化:空间清零memset(ETV, 0, sizeof(int) * graph->nodeNum);memset(LTV, 0, sizeof(int) * graph->nodeNum);// 更新ETV和LTVtopologicalOrder(graph, ETV, LTV);showTable(ETV, graph->nodeNum, "ETV: ");showTable(LTV, graph->nodeNum, "LTV: ");// 2. 计算边的ETE和LTE,直接输出关键路径for(int i = 0; i < graph->nodeNum; ++i){// 计算每个边的ETE和LTEArcEdge *edge = graph->nodes[i].firstEdge;while(edge){// 每个边的最早发生时间就是边的弧尾的ETV// 每个边的最晚发生时间就是边的弧头的LTV减去当前边的权重值if(ETV[i] == LTV[edge->no] - edge->weight){printf("<%s> ---%d--- <%s>\n", graph->nodes[i].show, edge->weight, graph->nodes[edge->no].show);}edge = edge->next;}}free(ETV);free(LTV);
}


2.2.6 优缺点辨析
- 优点
- 精确预测工期:科学计算项目的最短完成时间
- 聚焦关键任务:明确识别不能延误的任务,便于重点监控
- 便于动态调整
- 清晰展示依赖
- 缺点
- 忽视非关键路径:可能导致非关键路径因资源被挤占而转换为新的关键路径
- 模型复杂性:对于大项目,网络图复杂,难以手动管理
- 更新成本高
2.2.7 应用
- 建筑与工程项目管理
- 大型活动与展会策划
- 软件研发项目管理
- 流程优化和决策支持应用
三、小结
如果说,拓扑排序是确定一个可行的线性执行序列,那么关键路径就是整个项目最短工期的关键任务序列。拓扑排序是解决排序问题,关键路径是解决时间问题。
图的算法到这里就结束啦~ 下篇我们将开启算法界一种很常见的算法——排序算法(其方法可真是丰富了)期待~。

