当前位置：首页 > news >正文

【大数据技术02】统计学和模型

news 2025/11/11 9:45:35

参考资料：朝乐门。数据科学导论 [M]. 北京：人民邮电出版社，2020.

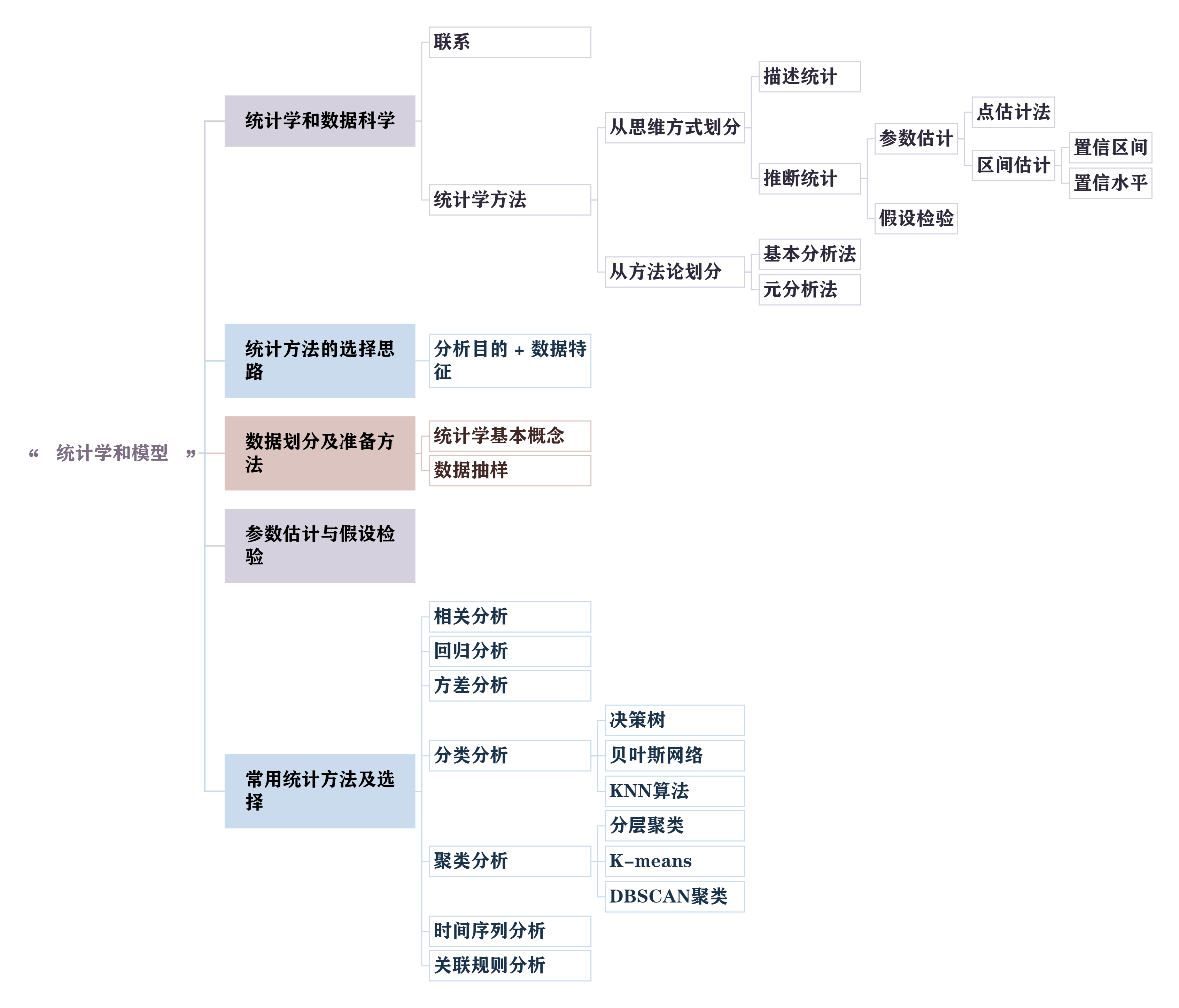
统计学和模型

文章目录

- 文章目录
- 二.统计学与模型
- - 1.统计学和数据科学
  - - 1.1 联系
    - 1.2 传统统计学方法
    - - 描述统计
      - 推断统计(参数估计 + 假设检验)
    - 1.3 基于统计的数据分析方法
    - - 基本分析法
      - 元分析法
  - 2.统计方法的选择思路
  - 3.数据划分及准备方法
  - - 3.1 统计学的四个基本概念
    - 3.2 数据抽样
  - 4.常用统计方法及选择
  - - 4.1 相关分析
    - 4.2 回归分析
    - 4.3 方差分析
    - 4.4 分类分析
    - 4.5 聚类分析
    - 4.6 时间序列分析
    - - **时间序列**
      - **拟合**
    - 4.7 关联规则分析

二.统计学与模型

1.统计学和数据科学

1.1 联系

首先，统计学是数据科学的主要理论基础之一

如图所示。数据科学的理论、方法、技术和工具往往来源于统计学。

第一篇以数据科学为标题的学术期刊论文 Data Science: An Action Plan for Expanding the Technical Areas of the Field of Statistics（International Statistical Review，2001）是统计学家威廉·S·克利夫兰完成的，该论文的发表引起了学术界的高度关注。数据科学领域常用的工具之一—R也是统计学家发明的语言。

1.2 传统统计学方法

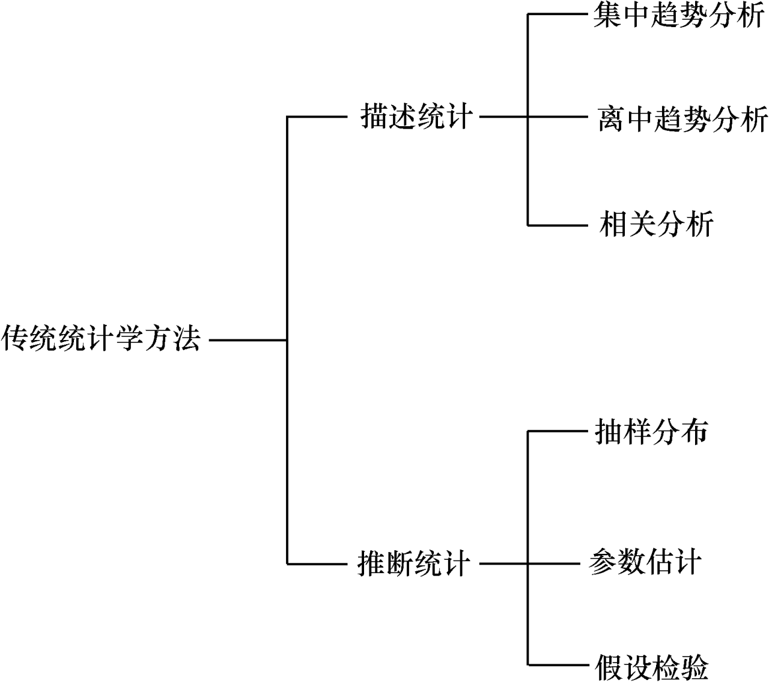
从思维方式来看，传统统计学方法可以分为两大类-描述统计与推断统计

描述统计

描述统计采用图表或者数学方法描述数据的统计特征，比如分布状态、数值特征等等

通常，描述统计分为3个基本类型

集中趋势分析(如数据平均数、位置平均数等等)

找数据的 “中心位置”，比如用平均数（如班级学生平均成绩）、中位数（数据排序后中间的数，避免极端值影响）等，反映数据的整体平均水平
离中趋势分析(如极差，分位差，平均查，方差，标准差，离散系数等等)

看数据的 “分散程度”，比如用标准差（数据偏离平均数的幅度，如成绩波动大小）、极差（最大值减最小值，快速了解数据范围）等，体现数据的稳定性；
相关分析(如正相关、负相关、线性相关、无关等等)

判断两个变量的 “关联关系”，比如分析 “广告投入” 和 “销售额” 是正相关（投入越多销售额越高）、负相关还是无关，用相关系数量化关联强度。

推断统计(参数估计 + 假设检验)

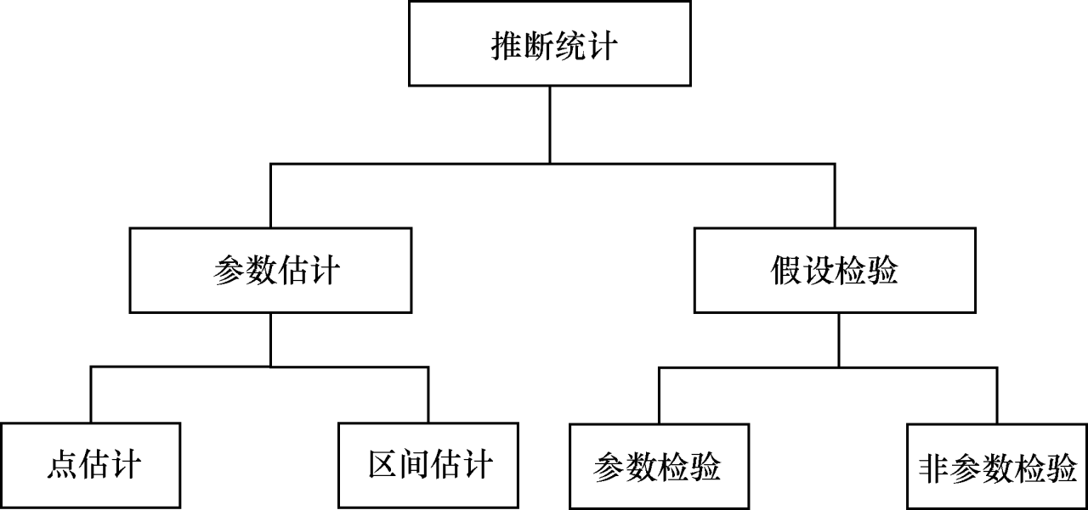
在数据科学中，推断统计有时需要通过样本对总体进行推断分析，常用的推断统计方法有两种

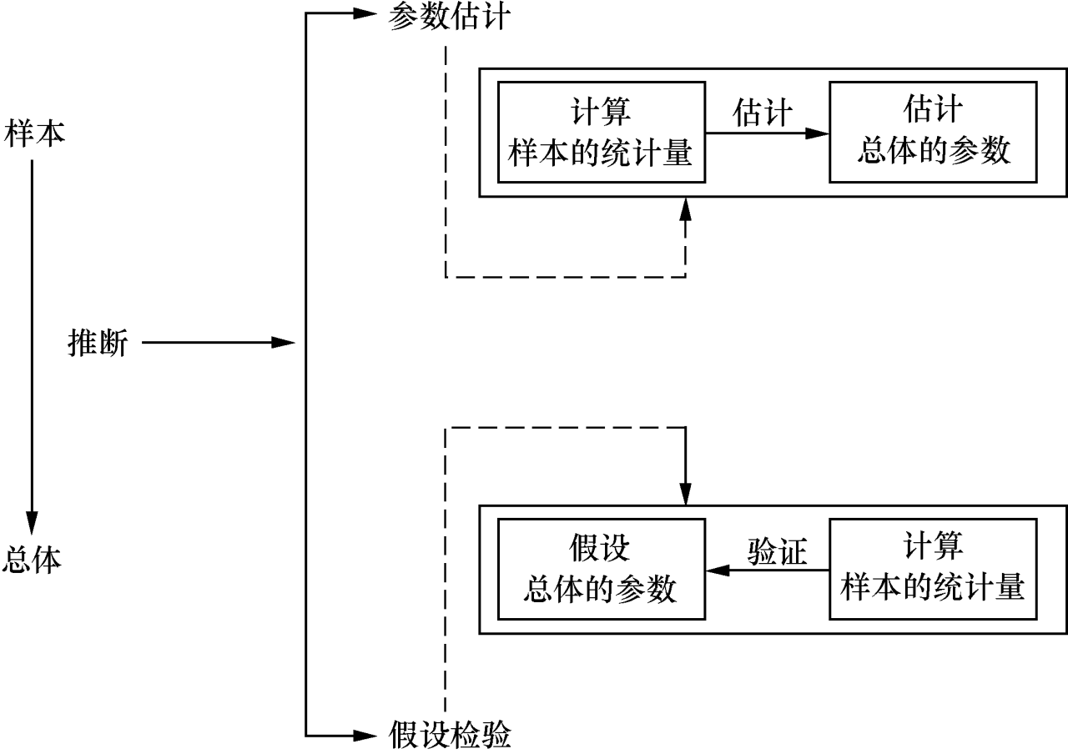
参数估计

目标是通过 “部分样本” 的信息，推断 “全部总体” 的特征

流程：
1. 计算样本的统计量（比如算出 100 个用户的平均消费额为500）
2. 用统计量估计总体的参数（用这 100 人的平均消费，推断 1000 万用户的平均消费）。
Eg.

用样本的统计量（如样本均值）估算总体的参数（如总体均值），比如从 1000 个用户样本中算出平均消费额，以此估计所有用户的平均消费额，还可进一步给出估算的 “区间范围”（如总体平均消费额在 80-100 元之间），提高结果可靠性；

参数估计分类

点估计：

先从总体中抽取一个样本，然后根据该样本的统计量对总体的未知参数作出一个数值点的估计，例如：用样本均值作为总体均值μ的估计值
区间估计：

区间估计是在点估计的基础上，给出总体参数落在某一区间的概率

例如：总体均值落在50-70之间的概率为0.93

通常，区间估计有两个重要的指标：置信区间和置信水平

置信区间（Confidence Interval）

是指由样本统计量构造的总体参数的估计区间，置信区间的最小值与最大值分被称为“置信下限”和“置信上线”

是一个 “数值范围”，表示我们通过样本估计出的 “总体参数可能存在的区间”。比如通过样本算出 “全校学生平均成绩的置信区间是 70-80 分”，意思是总体平均成绩有很大概率在 70 到 80 分之间。

置信水平（Confidence Level）

是指总体未知参数落在置信区间之内的概率，表示为1-α，其中：α是显著性水平，即总体参数未在区间内的概率

是一个 “概率值”（通常用百分比表示，如 95%），表示 “置信区间包含总体真实参数的可能性”。比如 95% 的置信水平，意思是如果我们重复抽样 100 次，会有 95 次算出的置信区间能包含总体的真实平均成绩。

假设检验

目标是先假设总体情况，再用样本数据验证假设是否成立

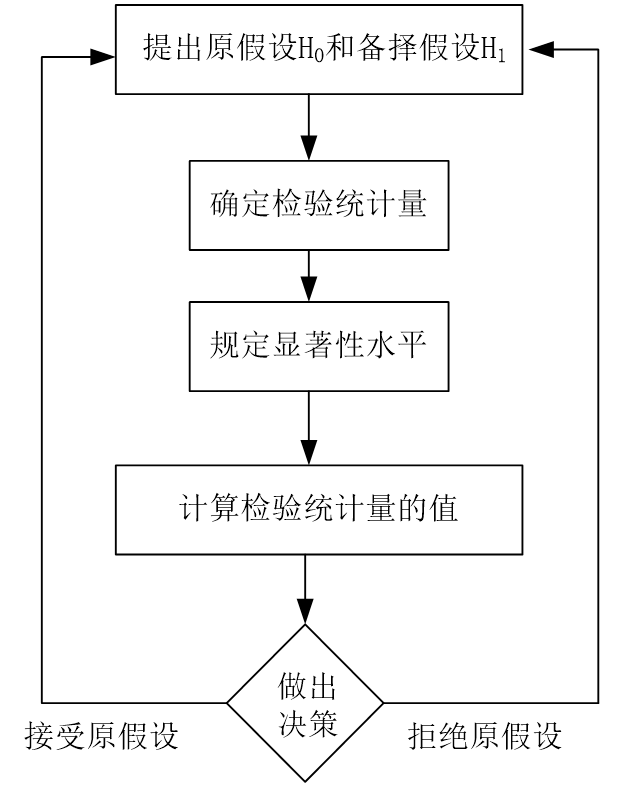
流程：
1. 提出原假设H0和备择假设H1：先对总体参数下一个 “待验证的假设”
  
  （如(H0)：“全校学生平均成绩是 75 分”，(H1)：“不是 75 分”）
2. 确定检验统计量：选一个能衡量“样本与假设差异”的统计量（如Z统计量，t统计量），用来量化差异程度
3. 规定显著性水平：设定“允许的错误概率（常用5%）”，表示错误拒绝原假设的最大概率
4. 计算检验统计量的值：用样本数据算出统计量的具体数值（如算出 Z 值为 2.1）。
5. 做出决策：对比统计量与显著性水平对应的临界值，判断是 “接受原假设”（认为假设成立）还是 “拒绝原假设”（认为假设不成立）
Eg.

先对总体特征提出假设（如 “某产品用户满意度超过 80%”），再用样本数据验证假设是否成立，比如抽取 500 个用户样本，若样本满意度仅 70%，则可能推翻原假设，常用于判断结论是否具有统计意义（而非偶然结果）。

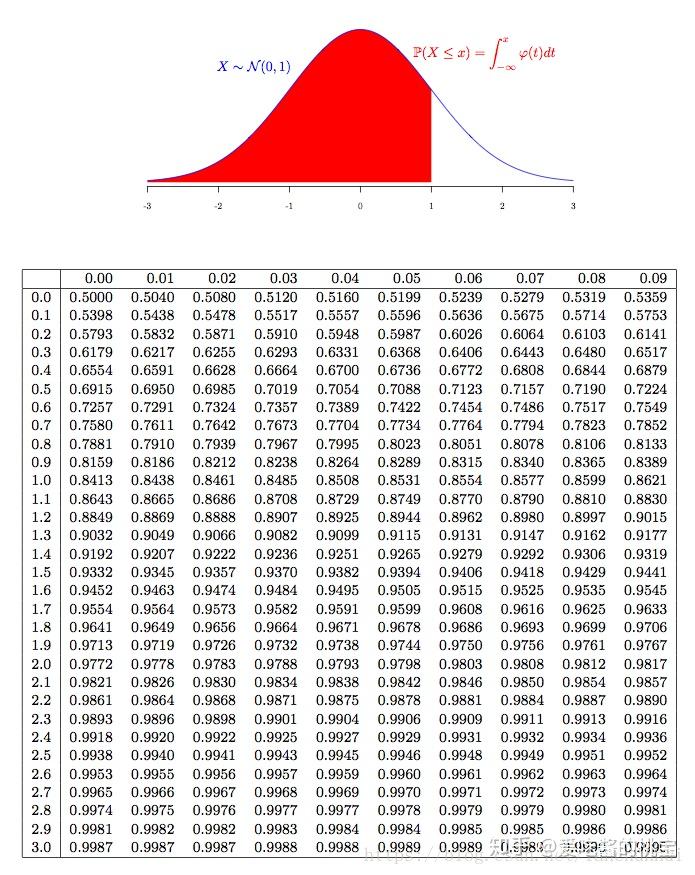
Z统计量表

z 值区间为((-1.96, 1.96))。此时 5% 的错误概率均分在分布两侧，每侧 2.5%，对应的临界值是 ±1.96，意味着若计算出的 z 值绝对值超过 1.96，就拒绝原假设。

1.3 基于统计的数据分析方法

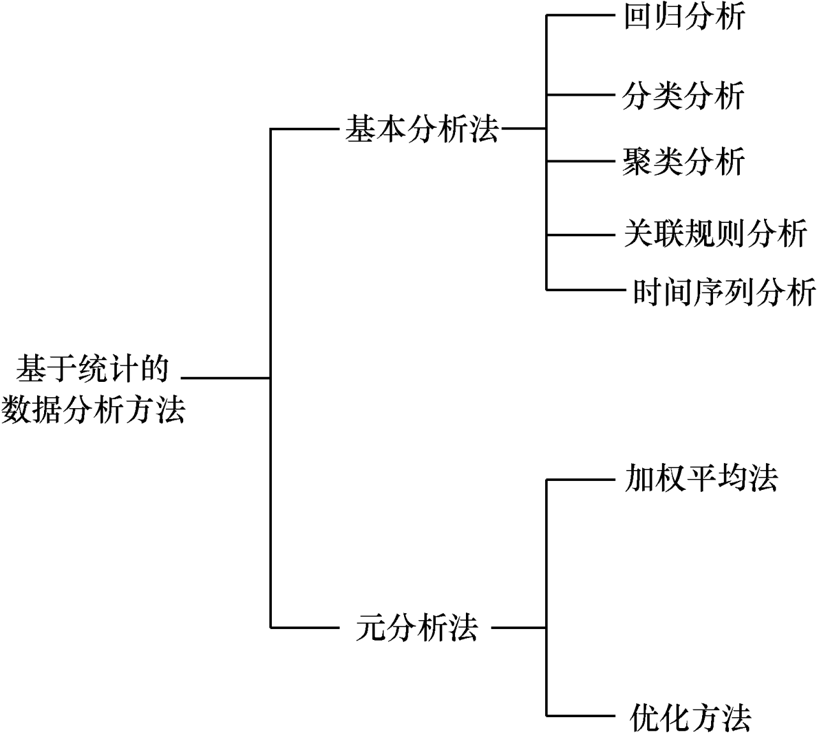
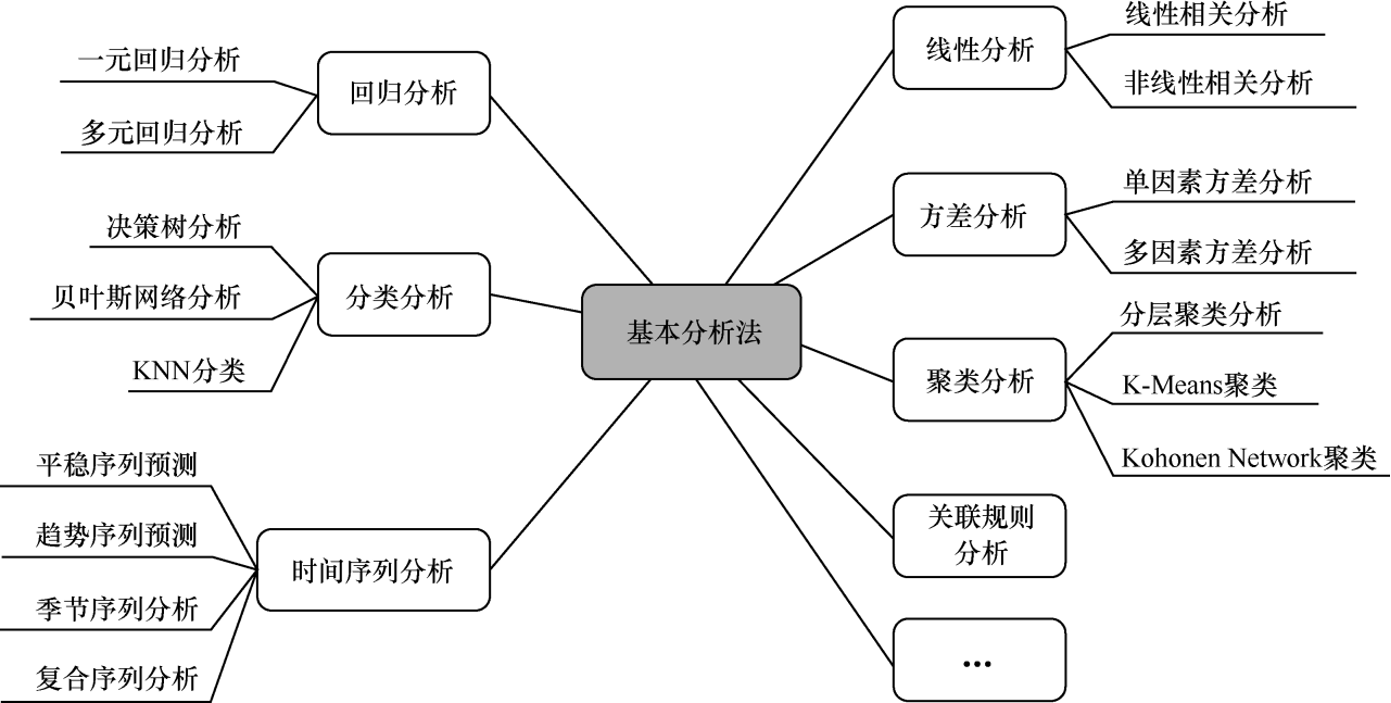
从方法论角度来看，基于统计的数据分析方法可分为基本分析法和元分析法

基本分析法

元分析法

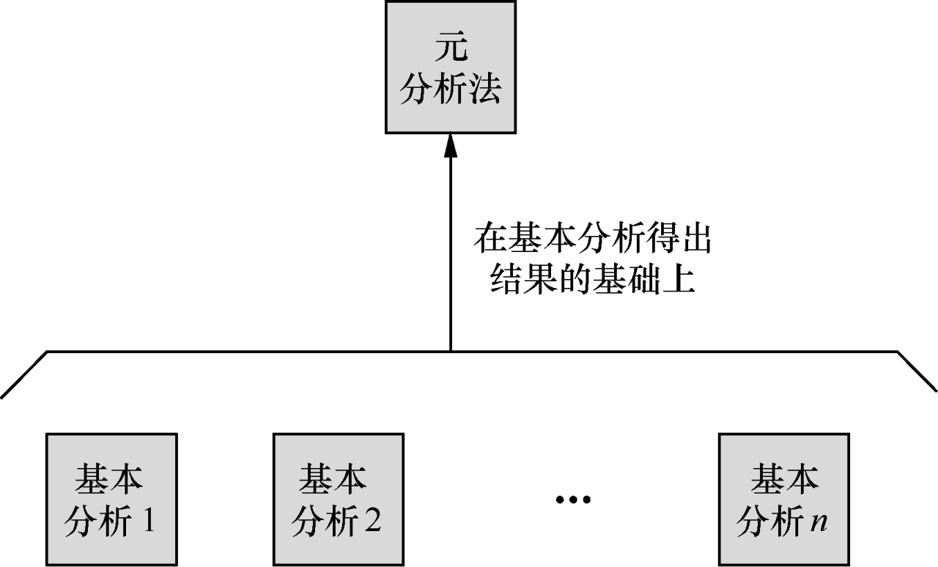
元分析法是对基本分析法得出的结果进一步分析的方法，常用的元分析法有：

加权平均法

给不同基本分析结果赋予不同权重（如样本量大、可信度高的结果权重更高），再计算综合结果，避免单一结果的偏差；
优化方法

通过统计模型调整或修正多个基本结果的差异，让最终结论更贴合实际情况。

Eg.

场景：要判断某款产品的 “用户推荐率”，用 “基本分析法” 做了 3 次独立调研 ——

调研 1（样本 100 人）：推荐率 60%（但样本里年轻人占 90%，可能偏乐观）；
调研 2（样本 500 人）：推荐率 45%（样本覆盖各年龄段，但地域集中在一线城市，可能有地域偏差）；
调研 3（样本 300 人）：推荐率 52%（样本均衡，但有 10% 受访者未认真填写，数据有噪声）。

这 3 个基本结果差异明显，直接取平均（（60%+45%+52%）/3≈52.3%）会忽略各自的偏差，结论不可靠。这时用 “优化方法” 就是：

识别偏差类型：先找出每个基本结果的问题（样本结构失衡、地域局限、数据噪声）；
用统计手段修正：
对调研 1：按全人群年龄比例 “调整权重”，降低年轻人样本的影响，修正后推荐率变为 55%；
对调研 2：加入地域差异系数，结合全国地域分布修正，推荐率变为 48%；
对调研 3：剔除无效数据，重新计算后推荐率变为 50%；

整合修正后结果：再基于修正后的 3 个结果（55%、48%、50%），用更合理的模型整合出最终推荐率（比如 51%）。

2.统计方法的选择思路

依据：分析目的和数据特征

分析目的：分析目的分为描述、分类、比较、预测和解释五种基本类型
数据特征：包括变量个数、自变量和因变量的划分、变量的相关性和数据类型等等
- 其中变量的相关性又可以分为线性相关、非线性相关、自相关、位置相关和时间相关等。数据类型有离散数据和连续数据之分。

先明确目标，再匹配数据特征:

分析目标：想通过数据解决什么问题？
若想 “描述数据长什么样”（如用户平均消费、成绩分布）→ 选描述统计（均值、标准差、图表等）；
若想 “给数据分类”（如把用户分成高、中、低价值群）→ 选分类分析（决策树、KNN 等）；
若想 “比较两组 / 多组数据差异”（如 A、B 两款产品的满意度是否不同）→ 选方差分析、假设检验等；
若想 “预测未来结果”（如下个月销量、用户是否会流失）→ 选回归分析、时间序列分析等；
若想 “解释变量间关系”（如广告投入和销售额的关联）→ 选相关分析、回归分析等。

数据特征：手里的数据适合什么方法？
看 “变量数量”：是单变量（如只分析 “年龄”）、双变量（如 “年龄” 和 “消费额”）还是多变量（如 “年龄 + 性别 + 收入” 影响消费）？多变量可能需要多元回归，单变量更适合描述统计；
看 “变量关系”：变量间是线性相关（如收入越高消费越线性增长）还是非线性相关（如收入到一定程度后消费增长放缓）？线性用线性回归，非线性可能需要非线性模型；
看 “数据类型”：是离散数据（如 “购买次数”“性别”）还是连续数据（如 “身高”“消费金额”）？离散数据可能适合分类、聚类，连续数据更适合回归、相关分析。

3.数据划分及准备方法

3.1 统计学的四个基本概念

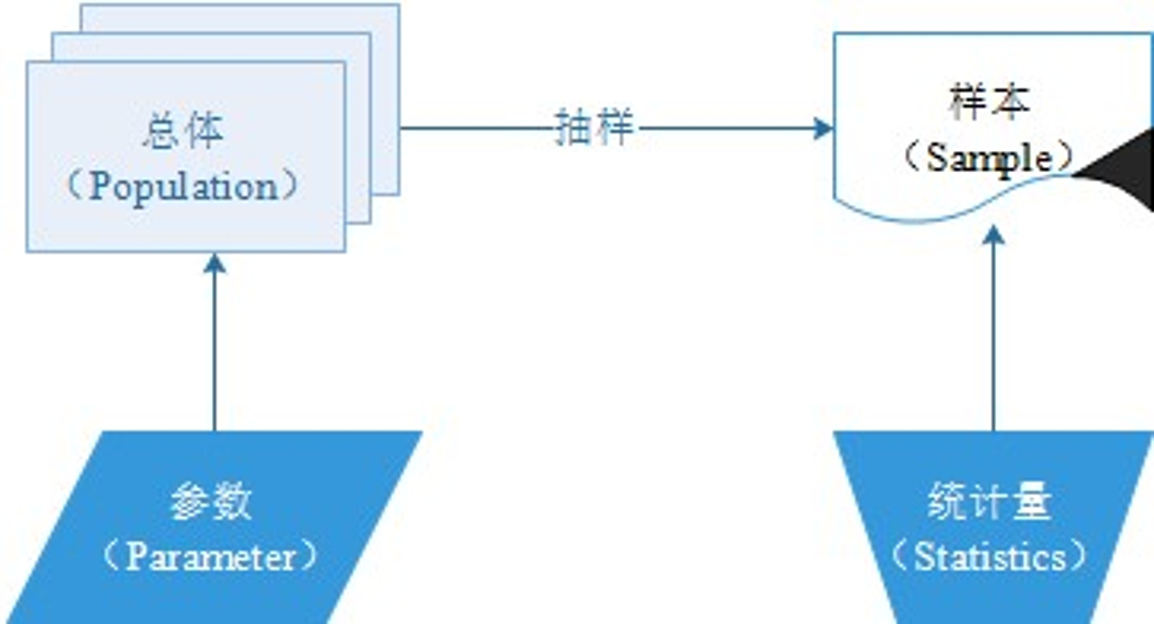
总体：研究对象的全部集合，是我们最终想了解的整体，比如想研究 “某学校全体学生的数学成绩”，那这所学校所有学生的数学成绩，就是 “总体”。
样本：从 “总体” 中抽取的 “部分集合”。因为直接研究总体（比如全校 1000 名学生）可能耗时费力，所以会抽选其中 100 名学生的数学成绩来分析，这 100 名学生的成绩就是 “样本”。
参数（Parameter）：指 “总体的特征值”，是我们想通过样本间接推断的总体属性。比如 “全校 1000 名学生的数学平均成绩”，就是总体的参数（这个值通常未知，需要用样本推测）。
统计量（Statistics）：指 “样本的特征值”，是直接从样本数据中计算出来的结果。比如抽选的 100 名学生的数学平均成绩，就是统计量（这个值可直接计算，用来估计总体的参数）。

总结：就是用样本的统计量去推断总体的参数，比如用 100 名学生的平均成绩（统计量），估算全校学生的平均成绩（参数）。

3.2 数据抽样

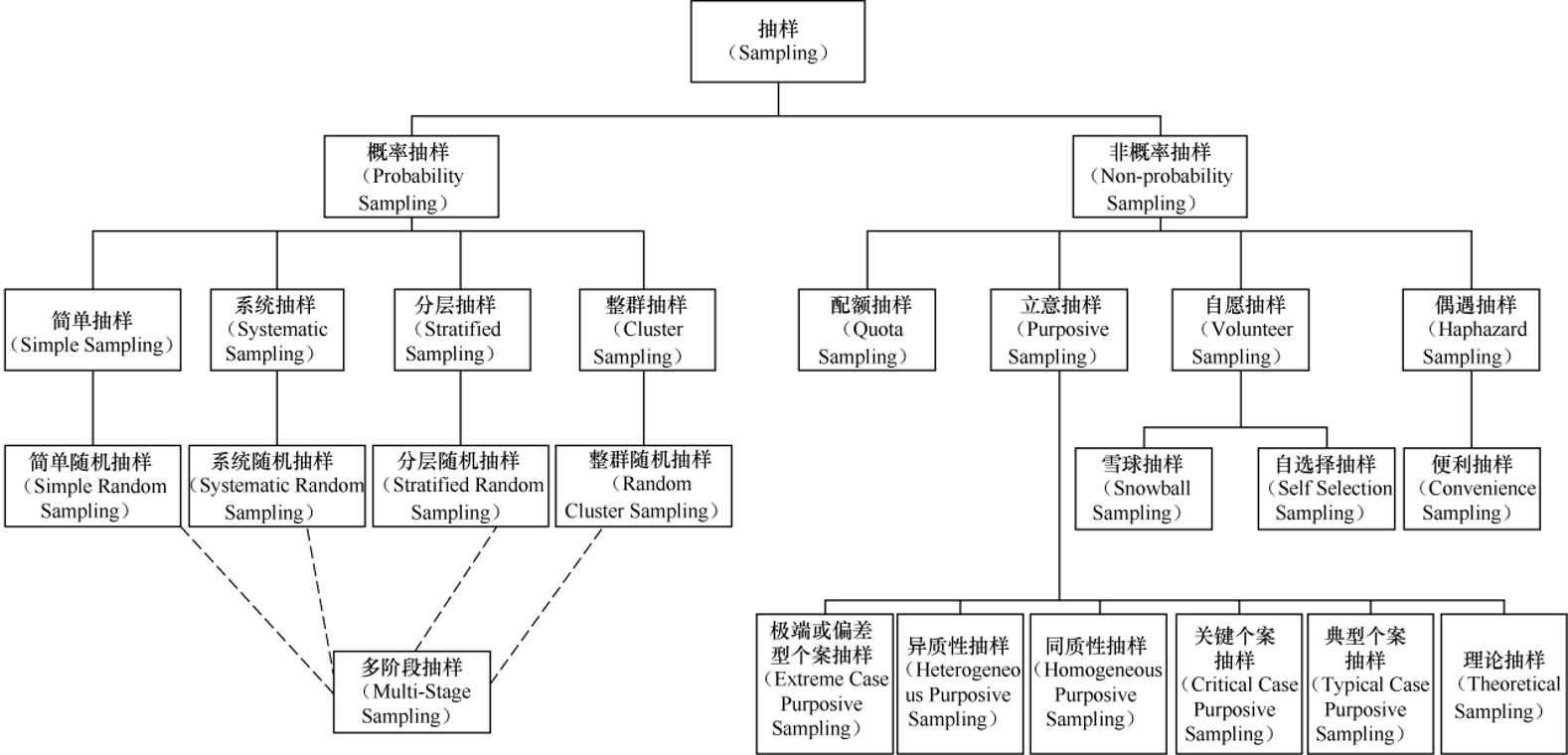
概率抽样：每个样本被选中的概率是明确的，结果更客观、能代表总体（适合需要推断总体的场景）；
简单抽样：核心是 “简单随机抽样”—— 给总体所有个体编号，随机抽选（如抽奖选样本）；
系统抽样：核心是 “系统随机抽样”—— 按固定间隔选样本（如从 1000 个用户中，每 10 个抽 1 个）；
分层抽样：核心是 “分层随机抽样”—— 先把总体按特征分层（如按年龄分 “青年 / 中年 / 老年”），再从每层随机抽样本（保证每层都有代表）；
整群抽样：核心是 “整群随机抽样”—— 把总体分成若干 “群”（如按班级分群），随机抽选整群作为样本；
多阶段抽样：是前 4 类方法的组合（如先分层、再系统抽样），适合大规模、复杂的总体（如全国人口抽样）。

非概率抽样：样本选中概率未知，结果偏主观，适合初步探索或特殊场景。
配额抽样：先设定各类别配额（如 “男 / 女各抽 50 人”），再按配额选样本；
立意抽样：按研究者主观判断选样本，又可细分 6 类（如 “极端个案抽样” 选最特殊的样本、“典型个案抽样” 选有代表性的样本）；
自愿抽样：样本主动参与（如网上问卷的参与者），细分 “雪球抽样”（样本推荐同类样本，如调研小众兴趣群体）、“自选择抽样”（用户自主报名参与）；
偶遇抽样：核心是 “便利抽样”—— 选容易接触到的样本（如在学校门口拦学生调研）。

4.常用统计方法及选择

4.1 相关分析

定义：

相关分析是对变量之间密切程度的度量----相关系数的分析方法

相关系数

总体相关系数（β）

描述 “整个总体中两个变量的真实关联程度”。但现实中我们几乎无法获取 “总体” 的全部数据，所以(\rho)通常是未知的。
样本相关系数（r）

用 “部分样本数据” 计算出的相关系数，是对(β)的估计。我们实际分析中用的就是样本相关系数r。

通常，由于总体相关系数（β）是未知值，所以一般采用样本相关系数（r）进行相关分析

相关系数r计算方法

通常，样本集x与y的相关系数r的计算公式如下(Pearson相关系数)：
$r=\frac{\sum(x-x)(y-y)}{\sqrt{\sum(x-x)^2\cdot\sum(y-y)^2}}$
其中，x和y分别是样本集x和y的均值；r为样本相关系数

其中：

r > 0：正相关
r = 0：无线性相关（可能存在非线性关联，只是线性关联为0）
r < 0：负相关

强度判断

4.2 回归分析

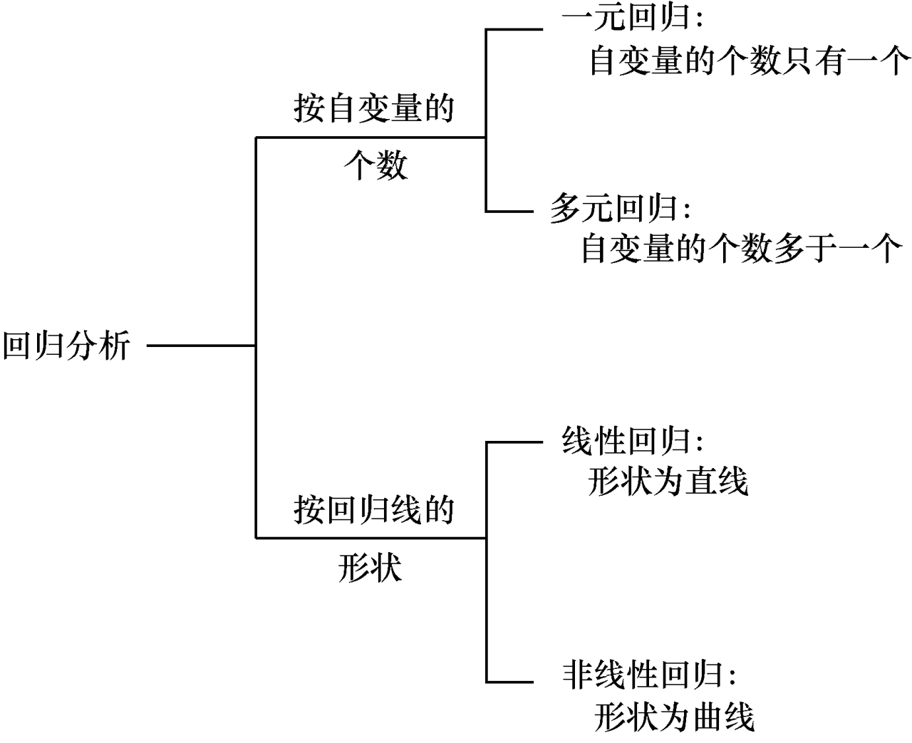
回归分析：

是以找出变量之间的函数关系为主要目的的一种统计分析方法

比较常见的回归分析方法有：一元回归，多元回归，线性回归和非线性回归

使用场景：

泛化场景类型核心逻辑跨领域示例（覆盖自然科学、社会科学、工程、生活）
1. 规律认知场景用数据验证 “经验 / 理论假设”，将模糊的 “定性判断” 转化为精确的 “定量结论” - 物理学：验证 “力、质量” 与 “加速度” 的关系（回归系数对应 “1 / 质量”）；- 社会学：验证 “教育年限” 与 “收入水平” 的正相关强度；- 生活：验证 “每日步数” 与 “体重变化” 的负相关程度。
2. 决策优化场景基于 “因素对结果的影响规律”，调整 “输入变量” 以实现 “输出结果最优” - 工程：调整 “原料配比”（输入）以实现 “产品合格率最高”（输出）；- 运营：调整 “折扣力度”（输入）以实现 “利润最大”（输出）；- 个人：调整 “学习时长 / 休息时间”（输入）以实现 “考试分数最高”（输出）。
3. 风险控制场景识别 “高风险结果” 的关键触发因素，提前干预以规避风险 - 金融：识别 “负债率、现金流”（输入）对 “企业违约风险”（输出）的关键影响，提前预警；- 医疗：识别 “血压、血糖”（输入）对 “并发症概率”（输出）的影响，制定干预方案；- 交通：识别 “车速、天气”（输入）对 “事故概率”（输出）的影响，优化限速政策。

只要存在 “历史数据中变量间的关联规律”，且该规律在未来短期内稳定，就能用回归模型将 “规律” 转化为 “可计算的预测结果”。
通过回归系数的大小、正负、显著性，量化 “每个输入变量” 对 “输出结果” 的 “贡献度”，帮我们从数据中提炼 “因果 / 关联规律”，而非仅靠经验判断。

场景中存在 “需要通过变量关系解决‘预测’或‘解释’” 的需求，回归分析就是一种可复用、可迁移的量化工具。

泛化场景类型	核心逻辑	跨领域示例（覆盖自然科学、社会科学、工程、生活）
1. 规律认知场景	用数据验证 “经验 / 理论假设”，将模糊的 “定性判断” 转化为精确的 “定量结论”	- 物理学：验证 “力、质量” 与 “加速度” 的关系（回归系数对应 “1 / 质量”）；- 社会学：验证 “教育年限” 与 “收入水平” 的正相关强度；- 生活：验证 “每日步数” 与 “体重变化” 的负相关程度。
2. 决策优化场景	基于 “因素对结果的影响规律”，调整 “输入变量” 以实现 “输出结果最优”	- 工程：调整 “原料配比”（输入）以实现 “产品合格率最高”（输出）；- 运营：调整 “折扣力度”（输入）以实现 “利润最大”（输出）；- 个人：调整 “学习时长 / 休息时间”（输入）以实现 “考试分数最高”（输出）。
3. 风险控制场景	识别 “高风险结果” 的关键触发因素，提前干预以规避风险	- 金融：识别 “负债率、现金流”（输入）对 “企业违约风险”（输出）的关键影响，提前预警；- 医疗：识别 “血压、血糖”（输入）对 “并发症概率”（输出）的影响，制定干预方案；- 交通：识别 “车速、天气”（输入）对 “事故概率”（输出）的影响，优化限速政策。

4.3 方差分析

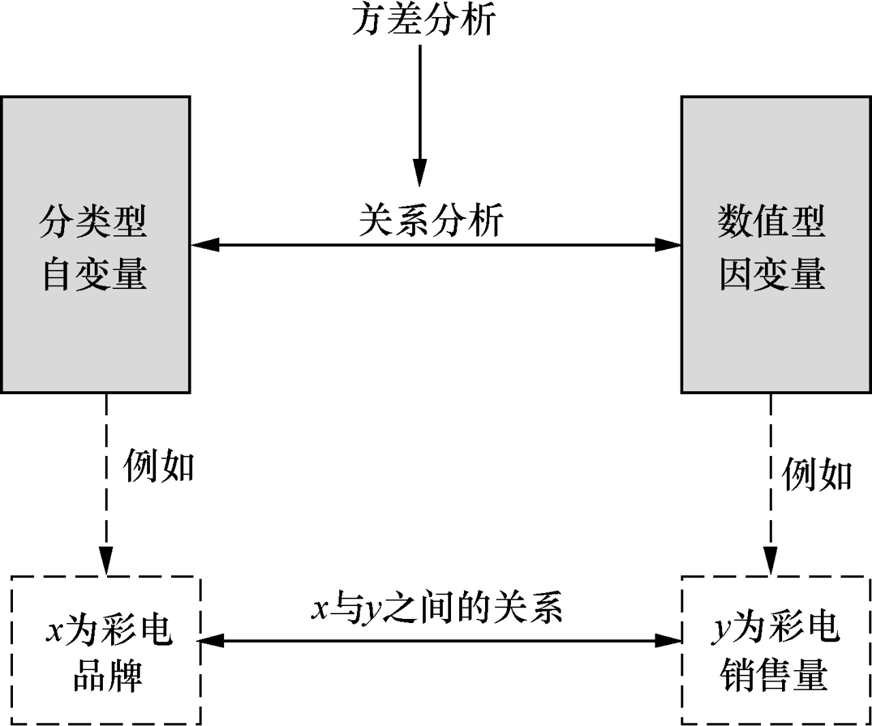
方差分析主要用于分析“分类型自变量”和“数值型因变量”之间的关系

分类型自变量：是 “类别化的影响因素”，如上图中的 “彩电品牌”（可分为 A、B、C 等类别），这类变量不能直接用数值衡量差异，只能通过 “类别” 来区分。

数值型因变量：是 “可量化的结果变量”，如上图中的 “彩电销售量”（用具体的销售数量来衡量）。

核心目的：分析类别对结果的影响是否显著，方差分析的核心是探究 “分类型自变量的不同类别，是否会导致数值型因变量产生显著差异”。以上图为例，就是要回答：“不同彩电品牌（A、B、C）的销售量，是否存在明显的差别？”

如何判断是否有显著影响？

答：通过分解因变量的“总变异”来判断影响的显著性

总变量 = 组间变异 + 组内变异
组间变异：由自变量类型不同导致的差异（如品牌 A 与品牌 B 的销量差距）；
组内差异：由“随机因素”导致的差异（如同一品牌内部不同门店的销量波动）。

若“组间变异远大于组内编译”（通过F统计量量化比较），则说明自变量的类型对因变量有显著影响，反之则无显著影响

方差分析分类：

单因素方差分析：仅1个分类型自变量（如仅分析 “品牌” 对 “销量” 的影响）；
多因素方差分析：多个分类型自变量（如同时分析 “品牌”“促销活动” 对 “销量” 的影响）。

F统计量

F 统计量的核心是用 “组间变异的强度” 除以 “组内变异的强度”，来判断 “类别差异是否真的重要”，

F 统计量：MSA ÷ MSEF 值的本质是 “类别导致的差异” 和 “随机导致的差异” 的比值：
若 F 值大（比如 F=5）：说明 “类别差异（如不同品牌的销量差距）远大于随机差异（如同一品牌门店的波动）”，意味着自变量类别对因变量影响显著；
若 F 值小（比如 F=0.8）：说明 “类别差异和随机差异差不多”，意味着类别对因变量影响不显著。

最后对比 “临界值” 下结论我们会先设定 “显著性水平”（常用 5%），再查 F 分布表得到对应 “临界值”（比如当自由度为 2 和 12 时，临界值约为 3.89）：
若计算的 F 值（如 5）＞临界值（3.89）：拒绝 “类别无影响” 的原假设，认为不同类别对因变量有显著影响；
若 F 值（如 0.8）＜临界值（3.89）：不拒绝原假设，认为类别影响不显

4.4 分类分析

**思想：**通过将大量数据分为若干个类别，在分别分析每个类别的统计特征，通过统计每个类别的统计特征反映数据总体的特征

核心是根据数据的特征差异，把相似的对象归为同一类，不同的归为不同类，主要用于解决 “数据分组”“类别识别” 类问题

应用场景
客户分群：帮助企业针对不同类客户制定差异化营销方案；
风险分类：金融领域把贷款客户分成 “低风险、中风险、高风险”，辅助信贷决策；
疾病诊断：医疗领域根据症状、指标把疾病分到不同类别，辅助诊断。

简单说，分类分析就是 “给数据贴标签、分群组”，让我们能从杂乱的数据中找到规律，为决策和管理提供清晰的类别依据。

Eg.

假设超市有 10000 名顾客（大量数据），先通过分类分析把他们分成 3 类：

类别 A：高频高消费人群（比如每周来 3 次，每次花 500 元以上）；
类别 B：低频刚需人群（比如每月来 1 次，只买生活必需品）；
类别 C：偶尔闲逛人群（比如季度来 1 次，只买促销商品）。

然后分别分析每个类别的统计特征：

类别 A：平均年龄 30-40 岁，女性占 60%，主要购买进口零食、高端日用品；
类别 B：平均年龄 45-60 岁，男性占 55%，主要购买粮油、调味品；
类别 C：平均年龄 20-30 岁，男女各半，主要购买网红零食、低价饰品。

这些 “分群后的统计特征” 合起来，就能反映数据总体（所有顾客）的特征

也就是把 “一大团模糊的数据” 拆成 “几个清晰的小群体”，再通过每个小群体的特点，拼出整个数据的全貌

**分类：**分类分析的算法有很多种，如决策树、决策表、贝叶斯网络（Bayesian Network）、神经网络、支持向量机、KNN 算法等。篇幅原因，这三个算法会单独出一篇文章。（以后替换为跳转链接）

4.5 聚类分析

与分类分析不同点：聚类分析所要求划分的类别是未知的（也就是数据无标签或标签不全）

聚类要求

每个分组内数据具有比较大的相似性
组间的数据具有较大不同

聚类算法

分层聚类、K-means聚类、DBSCAN聚类等等

这些我都会单独出文章（以后替换为跳转链接）

4.6 时间序列分析

时间序列

是按照时间顺序排列的数字序列

时间序列分析就是利用此组数列，并采用数理统计方法加以处理。进而预测未来事物的发展。

时间序列分析是：定量预测方法之一，他的基本假设有两条

承认事物发展的延续性，可应用过去数据，就能推测事物的发展趋势
考虑到事物发展的随机性，任何事物发展都可能受到偶然因素影响，为次要应用统计分析中加权平均法对历史数据进行处理

因此，时间序列预测一般采用三种实际变化规律：

趋势变化
周期性变化
随机性变化

拟合

对于短的或者简单的时间序列，可以使用趋势模型和季节模型加上误差来进行拟合

对于平稳时间序列，可用通用自回归滑动平均模型（Autoregressive Moving Average Model，ARMA）极其特殊情况的自回归模型、滑动平均模型来进行拟合
对于非平稳时间序列，则要先将观测到的时间序列进行差分运算，化为平稳时间序列，再用适当模型去拟合这个差分序列。

这些我都会单独出文章（以后替换为跳转链接）

4.7 关联规则分析

在关联规则分析中，“关联”指形如 X→Y 的蕴涵式。

其中，X 和 Y 分别称为关联规则的先导（Antecedent 或 Left-Hand-Side，LHS）和后继（Consequent 或 Right-Hand- Side，RHS）。

关联规则分析过程的阶段

关联规则分析的算法有很多种，如 Apriori 算法、FP-树频集算法和 Eclat 算法等

阶段 1：找出 “高频项目组（频繁项集）”

“项目组” 指一组同时出现的变量（如 “面包 + 牛奶”“手机 + 手机壳”），“高频” 指这些项目组出现的频率（支持度）达到设定阈值（比如至少出现 100 次）。

目的：先筛选出 “有足够出现频率” 的项目组 —— 只有高频项目组，才可能存在有价值的关联（低频项目组的关联多为偶然）。
举例：从超市 10 万笔交易中，先找出 “出现次数≥500” 的项目组，如 “面包 + 牛奶”（出现 800 次）、“尿布 + 啤酒”（出现 600 次）。

阶段 2：从高频项目组中生成 “关联规则”

对每个高频项目组，进一步判断 “X→Y” 的关联强度，常用两个指标衡量：

支持度：X 和 Y 同时出现的频率（如 “面包 + 牛奶” 在 10 万笔交易中出现 800 次，支持度 = 0.8%），确保关联的 “普遍性”；
置信度：当 X 出现时 Y 也出现的概率（如购买面包的顾客中，有 70% 同时购买牛奶，置信度 = 70%），确保关联的 “可靠性”。
目的：筛选出 “高支持度 + 高置信度” 的规则（比如支持度≥0.5%、置信度≥60%），才是有实际价值的关联（如超市可据此将面包和牛奶放在相邻货架）。

PPT 提到关联规则分析的核心算法有 3 种，各有特点：

Apriori 算法：最经典的算法，核心逻辑是 “高频项目组的子集也一定是高频的”，通过逐步筛选淘汰低频子集，减少计算量（适合中等规模数据）；
FP - 树频集算法：针对 Apriori 算法 “重复扫描数据” 的缺点，将数据压缩成 “FP - 树” 结构，只需扫描两次数据就能找出高频项目组（适合大规模数据）；
Eclat 算法：通过 “垂直数据格式” 存储数据（记录每个项目出现的交易 ID），用 “交集运算” 找高频项目组，适合处理稀疏数据。