3DGS致密化操作中的梯度计算

1、阅前声明

本文章内容仅为作者本人阅读学习所作笔记，不确保所有内容完全正确，后续根据个人学习进度会进行相应的补充更新。

2、3DGS的致密化策略

首先，最基本的，3DGS中判断某个高斯椭球A是否需要进行致密化的操作是：计算高斯椭球A在所有受影响的训练视图中的平均梯度。当这个平均梯度大于某一个阈值之后，就会进行高斯椭球的分裂。（备注：这里具体怎么分裂的暂时不做讨论）

也就是下面的这一个公式：

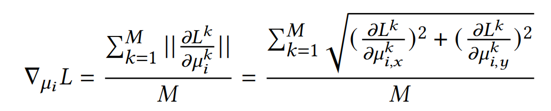
上面的公式中，M就是某个高斯椭球影响到的M张训练视图，这里的μ(x,y)和投影到2D平面的高斯椭球中心点。

这里有两个点需要注意：一是计算的是高斯椭球在所有受影响的视图中的平均梯度。这个受影响也就是说高斯椭球在这一张训练视图中有投影；二是某个高斯椭球A在一张训练视图中的梯度是如何计算的。

在此重点介绍一下这个：高斯椭球A在某一张视图中的梯度是如何计算的。

3、某个高斯椭球在某一张训练视图中的梯度是如何计算的

这里拿单独的一个高斯椭球A和受影响的一张训练视图B来举例分析。首先，高斯椭球A在这一张图片上会有一个2D椭球的投影，这个投影会覆盖一些像素。计算高斯椭球A在训练视图B中的梯度时，计算的是每个像素的损失对于三维空间中的高斯椭球中心的梯度之和。

所以在计算的时候，对于2DGS椭球覆盖的每一个像素点，其实都存在一个梯度。需要将这些梯度相加得到的结果，才是高斯椭球A在训练视图B中的梯度。

接下来就是使用链式法则的时候了：

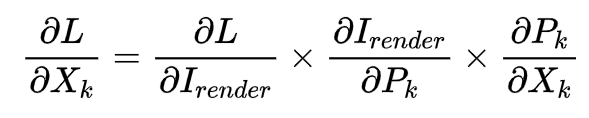
这个公式从右往左看，X_{k}就是三维空间中高斯椭球A的中心点坐标了，P_{k}是2D的高斯椭球中心点坐标，所以这个梯度对应的就是前向传播过程中3D高斯如何投影到2D高斯椭球的过程，反应的是3D中的点如何投影到2D中；右往左看第二个式子就是关于渲染的，也就是3D高斯中的α混合计算颜色的公式，某个像素的颜色是受2D高斯椭球（看他有没有覆盖到这个像素）影响的，单反应的是2D高斯椭球如何影响像素颜色；第三个公式就是损失的公式了，这个非常简单，损失就是像素值之差（L1，L2损失之类），3DGS中这个损失是用符号函数来实现的，反应的是渲染颜色和真实值偏离了多少。

总之，上面的公式最终的是记住一点，在最小的地方，计算某个像素对3D高斯椭球中心的位置偏导。其余的所有其他梯度，如高斯椭球在某一张视图中的梯度、高斯椭球在所有视图中的平均梯度等，都是基于这个最小的点来实现的。

4、关于维度变换的补充说明

关于上面的公式还存在比较有趣的一点：对于第二个偏导数，p_{k}是2DGS的中心点坐标，而x_{k}是3D高斯椭球的中心的坐标，在做这个转化的时候会出现的一个情况就是z这个坐标维度。因为前面在计算像素渲染的颜色对2d高斯椭球偏导的时候，只能够计算得到x和y两个方向的，但是最后一步需要传递到3D高斯椭球中的x,y,z三个维度上。这里是否存在一个维度消失的情况呢？

事实上，是不存在这个问题的，因为这里的z维度决定了深度信息，这个是由透视投影的规律决定的，而深度信息又决定了每一个像素的颜色（也就是α混合的过程）。所以总的来说，x,y,z三个维度的信息都会影响到后一步渲染的颜色。只不过z轴的这个维度信息会暂时的隐藏起来。