当前位置：首页 > news >正文

Whole-Body Control——双足机器人全身控制技术论文阅读笔记

news 2025/11/11 8:28:43

https://www.researchgate.net/profile/Luis-Sentis-2/publication/322414048_Whole-Body_Control_of_Humanoid_Robots/links/5f309671299bf13404b4089a/Whole-Body-Control-of-Humanoid-Robots.pdf

完整论文链接如上

或者在谷歌学术搜索，下载PDF

读文献，做仿真-》足底力估计/运动补偿/外设+线速度获取

ABS包括背景目的实验结果和结论

公式作用模块的输入输出和流程

文件筛选

Storkapp.me：文献鸟定时发送复合关键词的文献
Connectedpapers.com：Connected Papers输入文献名称和DOI可以获得相关论文知识图谱，追踪引用被引用关系

这篇论文主要关注的是全身体协调控制（Whole-Body Control, WBC）技术。以下是对每个部分的简要解释：

1. Introduction

这部分通常会介绍研究背景、目的和重要性。作者可能会讨论WBC的基本概念、其在机器人学中的应用以及当前的研究现状。此外，还可能概述论文的主要贡献和组织结构。

2. Classification of WBC Techniques

这一部分将对现有的WBC技术进行分类。作者可能会基于不同的标准（如控制策略、数学模型、应用场景等）来划分这些技术，并对每类技术的特点、优缺点和适用范围进行详细说明。这有助于读者全面了解WBC领域的技术多样性。

3. Case studies of torque-based closed-form WBC methods

这部分将通过具体案例来展示基于力矩的闭式WBC方法的应用。作者可能会选择一些具有代表性的研究或实验，详细描述这些方法是如何设计和实现的，以及它们在实际场景中的表现。通过案例分析，读者可以更直观地理解这些方法的工作原理和效果。

4. Software for WBC

这一部分将介绍用于实现WBC的软件工具和平台。作者可能会讨论常用的编程语言、库和框架，以及它们在WBC开发中的优势和局限性。此外，还可能涉及软件架构、算法实现和调试技巧等内容，为研究人员和工程师提供实用的指导。

5. Future Directions and Open Problems

最后，作者将展望WBC领域的未来发展方向，并指出当前存在的开放问题和挑战。这部分内容可能包括新技术趋势、潜在的研究热点、需要解决的关键难题等。通过探讨这些问题，可以激发读者的兴趣和思考，促进该领域的进一步发展。

2 Classification of WBC Techniques

WBC 能做什么？

目标：在一个闭环控制系统中，同时执行多个任务（可能并行，也可能冲突）。
约束条件：必须满足物理世界的限制，例如：
- 接触约束（如脚踩地、手抓物）
- 机械传动限制
- 轮式机器人的滚动约束

✅ 这体现了 WBC 的“协调性”和“现实可行性”。

二、什么是“任务”（Task）？——任务的类型

任务可以是简单或复杂的控制目标：

类型	示例
简单任务	控制某个末端执行器（如手或脚）在笛卡尔空间中的位置（引用 [6]）
复杂任务	涉及动态稳定性的物理指标，例如：

零力矩点（ZMP） [12] → 用于双足行走稳定性
捕获点（Capture Point） [13] → 预测机器人是否会摔倒
质心动量（Centroidal Momentum） [14,15] → 控制整体运动状态
重力刚度（Gravitational Stiffness） [16,17] → 提高抗扰能力 |

🧠 说明：WBC 不仅控制“动作”，还控制“稳定性”。

三、WBC 的两大分类维度

作者提出可以从两个正交维度来划分 WBC 方法：

维度一：输出类型 → 速度 vs 力矩（Velocity vs Torque）

类型	输出	实现方式	特点
速度型控制器	关节速度（joint velocities）	上层输出速度指令，底层用位置/速度环跟踪
力矩型控制器	关节力矩（joint torques）	上层直接输出力矩，底层通过力矩或阻抗控制器实现

📌 关键区别：

输出不同 → 反馈控制律的设计位置不同
影响闭环性能、响应速度、与底层控制器的集成方式

⚠️ 当前争议：

是否力矩控制一定优于速度控制？
实际上仍存在争议。例如：
- 力矩控制可实现高精度力跟踪
- 但在级联结构中（力矩+位置控制），其位置带宽较低 [18]
作者表明：本文不深入比较性能优劣，只做分类描述

维度二：求解方法 → 闭式解 vs 优化法（Closed-form vs Optimization-based）

方法	特点	举例（见表格）
闭式方法（Closed-form）	使用解析公式快速计算控制输出，实时性好，但灵活性较低	Kajita [10], Gienger [19], Mansard [20] 等
优化方法（Optimization-based）	将任务建模为优化问题（如QP），可处理优先级、约束、冲突任务，更灵活但计算量大	Kanoun [24], Escande [25], Del Prete [27] 等

🔍 这个分类反映了算法设计哲学的差异：效率 vs 灵活性

四、综合分类表（Table 1）解读

作者提供了一个清晰的四象限分类表，将主流 WBC 方法按两个维度归类：

	闭式方法	优化方法
速度型	Kajita [10]<br>Gienger [19]<br>Mansard [20]	Kanoun [24]<br>Escande [25]
力矩型	Sentis & Khatib [11]<br>Dietrich [21]<br>Mistry & Righetti [22]<br>Moro [23]	Salini [26]<br>Del Prete [27]<br>Herzog [28]<br>Dai [29]<br>Feng [30]<br>Koolen [31]<br>Hopkins [32]

📌 观察发现：

早期经典方法多为闭式 + 速度型（如 Kajita 的动量控制）
现代主流趋势是优化 + 力矩型，因其能更好处理复杂任务和约束
Sentis & Khatib [11] 是唯一一个闭式力矩控制器的代表，具有里程碑意义

✅ 总结：这段讲了什么？

维度	内容总结
WBC 的功能	协调多个任务（简单或复杂），同时满足物理约束
任务类型	从末端位置到动态稳定性指标（ZMP、动量等）
分类标准1	输出是关节速度还是关节力矩 → 影响控制架构与性能
分类标准2	使用闭式解析解还是优化求解 → 影响灵活性与实时性
现状趋势	从早期速度型闭式方法，发展到现代力矩型优化方法为主流

雅可比复习

每一维的笛卡尔位姿都由六个关节共同决定，由微分方程得到位姿雅可比。
$y_1 = f_1(x_1, x_2, x_3, x_4, x_5, x_6) \\ y_2 = f_2(x_1, x_2, x_3, x_4, x_5, x_6) \\ \vdots \\ y_6 = f_6(x_1, x_2, x_3, x_4, x_5, x_6)$
即构建出笛卡尔坐标和关节坐标的关系。
由微分法则
$\delta y_1 = \frac{\partial f_1}{\partial x_1} \delta x_1 + \frac{\partial f_1}{\partial x_2} \delta x_2 + \cdots + \frac{\partial f_1}{\partial x_6} \delta x_6 \\ \delta y_2 = \frac{\partial f_2}{\partial x_1} \delta x_1 + \frac{\partial f_2}{\partial x_2} \delta x_2 + \cdots + \frac{\partial f_2}{\partial x_6} \delta x_6 \\ \vdots \\ \delta y_6 = \frac{\partial f_6}{\partial x_1} \delta x_1 + \frac{\partial f_6}{\partial x_2} \delta x_2 + \cdots + \frac{\partial f_6}{\partial x_6} \delta x_6$
改为张量形式： $\delta Y = \frac{\partial F}{\partial X} \delta X$
两端同时对时间求导：
$\dot{Y} = J(X) \dot{X}$
转化为
${}^0v = {}^0J(\Theta) \dot{\Theta}$
即构建出笛卡尔速度和关节速度的关系。
因此有 $\dot{\Theta} = J^{-1}(\Theta) v$ 。

2.1 Velocity-based WBC using closed-form techniques

可以理解为在实现第一个动作的要求下，在剩余自由度空间内寻找第二个任务的解，同时执行

第一种WBC方式我是看明白了，貌似就是用伪逆雅可比的速度计算+优先级控制，同时对人形机器人做了P投影驱动关节的修正

介绍第一种速度控制的闭式WBC

对于一个任务就是一个 $\dot{x_i}$ ，，多个任务需要同时完成，比如边走边开门，这就需要开门这种次优先级动作避让移动这个高优先级动作。

一个关节在同一时刻只能执行一个运动，但我们希望机器人“同时”完成多个任务（如移动身体和开门）。

你的直觉是对的：物理上，关节不能“分身”去干两件事。但 WBC 的巧妙之处在于：它通过任务分解 + 零空间协调，让一个关节的运动“同时服务于多个目标”，而不是“分别执行两个独立动作”。

举个例子：7自由度机械臂（如人臂）

你只想控制手的位置（3D空间），但你有7个关节。
这意味着：有无穷多种关节组合可以达到同一个手的位置。
这些“不影响手位置”的额外自由度，就构成了任务的零空间。

可以理解为在实现第一个动作的要求下，在剩余自由度空间内寻找第二个任务的解，同时执行

总述综上，我们可以把求组合运动的关节速度控制写成下式，

但是，非方阵无逆，因此引入MP伪逆：

其中， $\dot{q_i}$ 表示关节速度， $\dot{x_i}$ 表示第 i 个任务的速度目标，而 $(\tilde{J}_i^\#\ )$ 是与 $(\tilde{J})_i$ 相关的一致伪逆矩阵。
控制动作 $\dot{x_i}$ 不仅可以是笛卡尔空间中的速度（如平移和旋转速度），还可以是其他基于速度的度量，例如关节速度、质心动量等。

文献中提出了多种伪逆矩阵的计算方法，其中，MP伪逆是最简单的一种形式：

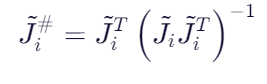
优先级避让协议——通过将低优先级任务限制在高优先级任务的零空间内（使用累积投影矩阵实现）

零空间（Null Space）和累积投影矩阵（Cumulative Projection Matrix）

在零空间内的关节速度变化不会引起末端执行器速度的变化

它是一个投影算子（projection operator），作用是：把任何关节速度 $\dot{q_i}$ 投影到前面所有高优先级任务都不受影响的空间中。

为了防止次优先级的任务计算的关节变量会影响高优先级任务的关节变量，因此在计算低优先级的任务的关节变量时，一定要在高优先级任务的零空间内，确保不影响高优先级任务。而实现这一方法的就是累计投影矩阵，它是一个投影算子（projection operator）把任何关节速度 $\dot{q_i}$ 投影到前面所有高优先级任务都不受影响的空间中，只要在这个投影矩阵内计算的雅可比的逆，都是可取的。

因此将无优先级的（1）式改为（3）式：

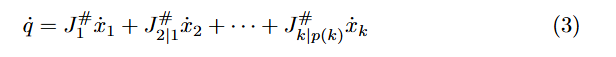
其中定义：J优先级限制雅可比为该关节变量雅可比的结果投影到前i-1个关节的零空间内

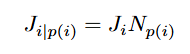
其中定义：Np投影算子为前i-1个投影算子联积

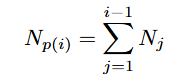
具体计算为：

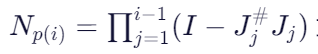
此外，MP伪逆也可以替换为其他的伪逆方法。

最后，对于人形机器人来说：

人形机器人驱动协议

人形机器人躯干没有主动驱动器但是却有6个自由度，但是我们只能控制主动关节，因此需要投影矩阵P标记出来哪些关节可以被驱动。

处理类人机器人时的特殊考虑

为什么需要投影矩阵 P，以及为什么要将 n 维速度映射到 na 维速度？

浮动基座

机器人基座（通常是躯干）在空间中的自由度没有被固定，而是“漂浮”在空中，其运动完全由内部关节的运动和外部接触力（如地面反作用力）共同决定。

主动关节与被动关节

为什么需要投影矩阵 P？——因为基座是“被动”的

投影矩阵 P

在处理类人机器人（或更一般的浮动基座机器人）时，公式(1)和(3)需要左乘一个投影矩阵 P。这个矩阵的作用是将 n 维速度映射到 na 维速度，其中 na 是机器人活动关节的数量。

力域雅可比复习

虚功原理

功是标量，在哪做功都一样，因此在笛卡尔系的功=在关节坐标系的功

有 $\mathbf{F} \cdot \delta \chi = \tau \cdot \delta \Theta$
F是作用在末端执行器的笛卡尔力
δX是末端执行器的微位移
τ是关节力矩
δΘ是关键微位移

又，位移雅可比：
$\delta \chi = J \delta \Theta$
带入有：
$\mathbf{F}^T \delta \chi = \tau^T \delta \Theta$
$\mathbf{F}^T J \delta \Theta = \tau^T \delta \Theta$
$\mathbf{F}^T J = \tau^T$

有
$\tau = J^T \mathbf{F}$

我们对外部力和关节力做了映射。

2.2 Torque-based WBC using closed-form techniques

力域任务用表示，这是一个PD控制

根据上文，关节力矩可以得到如下公式

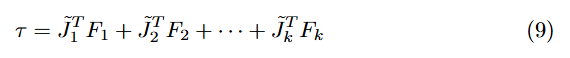
任务的重要性可以通过两种主要方式来表达：层次化（Hierarchical） 和 加权（Weighted）。

层次化与2.1一样。

加权则需要对权值做调整。

两种方案各有优劣，比如分层就在于如何定义任务的顺序，权值就在于如何调整权值。

2.3 Velocity/torque-based WBC using optimization tech-
niques HPQ

对于每一个任务，按照优先级排序，选择一个优化变量，构建运动学方程，转化为等式约束
然后构建约束不等式
将等式不等式参数化为，等式两侧就是一条完整的约束然后解决QP问题：依次读取约束，在满足此前等式/不等式约束的前提下，最小化任务的误差函数和w惩罚项接着更新等式约束。对于本轮的不等式约束，一条一套抽出来看，如果小于边界，则继承；如果超过边界一点点，但是被w保住了，那么将其冻结住，转化为等式约束

力矩任务和速度任务本质上还是PD等式控制任务

而实际环境中会存在力矩和空间约束，因此需要不等式描述这部分约束。

总而言之，除了利用前文的分层/加权雅可比（无法处理不等式，继而无法处理约束），也可以用等式和不等式解决速度和限制问题。

x是优化变量，可以选择关节速度、关节加速度、关节力矩：

优化变量	优点	适用场景
关节速度	计算快，适合运动规划	无接触、少约束的运动任务
关节加速度	可直接接入动力学方程	需要处理接触力、平衡等
关节力矩	直接控制输出，适合力控	柔顺控制、力交互任务

然后动力学模型可以将其他变量全整合到与优化变量相关的等式/不等式中，如此，优化该变量，也自然优化了其他变量。

动力学模型就是“桥梁”：它把速度、加速度、力矩、接触力全都耦合在一起。

类比：汽车控制

你不是“先决定车速，再决定油门”，而是：
设定目标速度（任务）
控制器根据当前速度、坡度、风阻（动力学）计算需要多大油门（力矩）
油门 → 加速度 → 速度变化

整个过程是一体化的反馈控制，不是“两步迭代”

我们用例子理解

场景：人形机器人从远处走向门，并伸手开门

机器人有两个任务（按优先级排序）：

高优先级任务：保持平衡（质心在支撑多边形内，双脚不滑动）
低优先级任务：右手移动到门把手位置（完成开门动作）

同时有物理限制：

关节角度不能超限
关节速度不能太大
脚与地面的接触力必须在摩擦锥内（防止打滑）

接着选用合适的优化参数，并建模

第一步：定义优化变量

设优化变量为关节加速度（也可以是或，这里用更适合动力学建模）：

第二步：将任务和限制转化为等式/不等式

✅ 任务1（高优先级）：保持平衡 → 等式约束

控制质心加速度，使其轨迹稳定。

使用质心雅可比 和其导数，有

我们希望质心加速度满足某个期望值（比如缓慢前进而不倾倒）：

写成等式约束：

✅ 任务2（低优先级）：手到门把手 → 优化目标

我们希望手尽快接近目标，但不能破坏平衡。

手的加速度关系：

设期望的手加速度（来自 PD 控制）：

我们不要求完全满足，而是在满足任务1的前提下，最小化误差：

限制

✅ 物理限制 → 不等式约束

1. 关节加速度限制

电机响应有限，加速度不能太大：

（是，是）

2. 摩擦锥约束（防滑）

脚底不能滑动，接触力必须在摩擦锥内。

接触力与的关系由动力学方程给出：
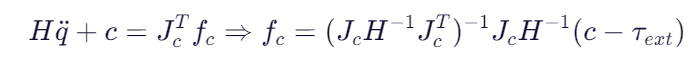
摩擦锥约束（简化为线性近似）：

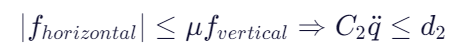
3. 松弛变量的作用

有些约束（如摩擦锥）可能在某些状态下无法完全满足。我们引入松弛变量 ，允许轻微违反，但要惩罚它。

例如：（允许轻微违背摩擦锥约束）
然后在目标函数中加，让求解器“尽量不违反”。

算法

算法整体流程

初始化：
- 设置等式约束系统 $\bar{A}_0$ 和
- 设置不等式约束系统 $\bar{C}_0$ 和 $\bar{d}_0$
迭代优化：
- 对于到：
  - 求解二次规划问题以获得
  - 更新等式和不等式约束系统(约束矩阵 $\bar{A}_{k+1}$ ：将之前的约束 $\bar{A}_k$ 加上这一次的约束 ${A}_k$ ，目标向量：将之前的目标加上本次求得的最优解)
  - 检查并调整不等式约束(把当前迭代的约束一条条从Ck中取出验证，如果满足则更新新的约束，如果勉强满足则将不等式约束加入等式约束)
    这种情况下，使得不等约束卡在了w这个边界上，已经轻微违反了约束，因此为了防止优化恶化，将这个约束改为等式约束。

求解细节：求解二次规划问题以获得

在第k+1次求解时，QP问题的求解意味着在满足前k次的等式/不等式约束前提下，最小化本次的任务误差函数，并最小化w违规惩罚。

总结：

步骤	操作	目的
1. 构建 QP	用构建约束组	继承前面所有必须满足的条件
2. 求解 QP	最小化任务误差 + 松弛惩罚	找到当前任务下的最优解
3. 更新约束	检查哪些不等式被违反，转为等式	“冻结”关键状态，防止后续破坏
4. 进入下一层	用开始下一轮	继续处理下一个任务

2.4 基于力矩优化的全身体控制（Torque-based WBC）

我们必须把优化变量扩展为，才能真正实现“力-运动”协同控制。

在基于力矩的全身体控制（Torque-based WBC）中，为了更精确地建模和控制机器人，我们需要将优化变量从单纯的关节加速度扩展为一个包含多个物理量的复合任务向量：

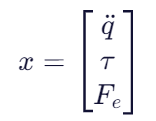
a. 关节加速度 ()
b. 关节力矩 ( $'\tau_i$ )
c. 接触力 ( $'F_{ei}$ )

然后，这个复合向量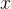就作为二次规划（QP）问题的优化变量参与求解。

如何构建这个 QP 问题？

1. 目标函数（最小化任务误差 + 控制量平滑）

例如，我们希望手部运动准确，同时力矩不要太大：

2. 等式约束（必须满足）

(1) 系统动力学方程（关键！）

这是基于力矩 WBC 的核心约束：

这是一个线性等式约束（在固定时）：

其中：

(2) 任务等式约束

例如：保持质心加速度为某值：

3. 不等式约束（物理限制）

(1) 关节力矩限：

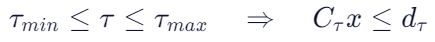
(2) 摩擦锥约束（接触力不能打滑）：

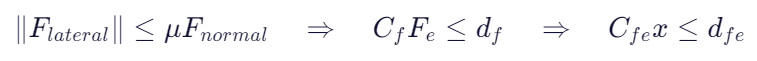
(3) 关节加速度限（可选）：

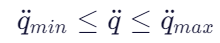
3 基于力矩的闭环形式全身控制实现（WBCR）

层次化任务优先级方法（Section 3.1），该方法通过建立任务之间的层次结构来实现全身控制。
权重指定任务相对重要性方法（Section 3.2），该方法通过为不同任务分配权重来确定它们的相对重要性。
混合解决方案（Section 3.3），结合了层次化和权重的方法，以提供更灵活的全身控制策略。

此外，第3.4节通过一个示例展示了这三种方法在系统行为上的差异。

这意味着机器人会首先确保关节不超出极限，然后保持平衡，接着控制手部位置，最后调整对称姿势。

3.1 WBOSC（Whole-Body Operational Space Control）

这是我们的优化目标，在前文提到过，我们直接用逆雅可比+零空间+累计投影矩阵避让完成了分级控制。

你看看我理解的对不对，WBOSC首先对任务分级，JLC>COM>HAND>SYM任务，然后获取qv ql xcom xfeet xhand xtar q qmid，计算势能场。接着将势能场（误差量场）转化为力，定义误差e和误差变化率e`，然后用PD控制器定义力补偿，是笛卡尔空间的力域。接着要计算关节空间的加速度，因此要进行雅可比+广义逆，依次计算零空间，并对下一个目标的关节变量进行累计投影矩阵运算，确保前面的优先结果不变。最后执行。

3.2 Attractor-based Whole-Body Motion Control 加权式吸引子方法

首先可以设定/学习一组权重，为各个任务分配权重。
然后机器人感知自身，每个吸引子根据传感数据计算自身的参考力矩输出（此时已经是力矩了）。
然后决策力矩就是线性加权求和。
最后要加上重力补偿项。

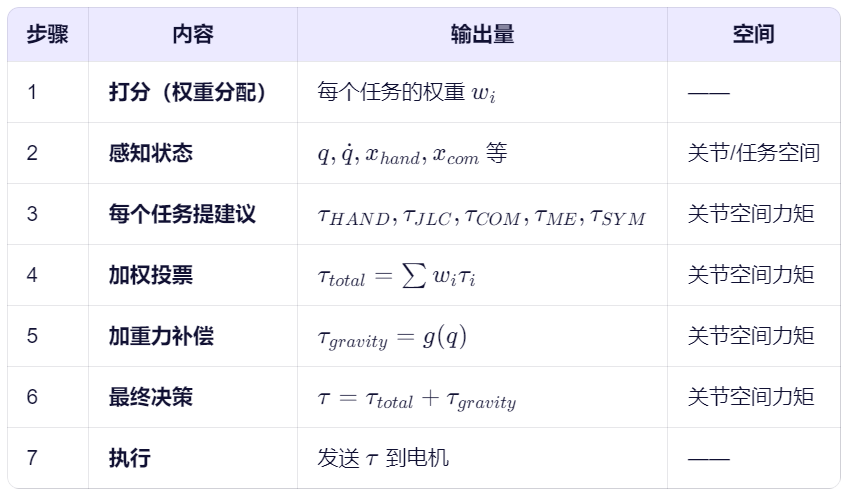
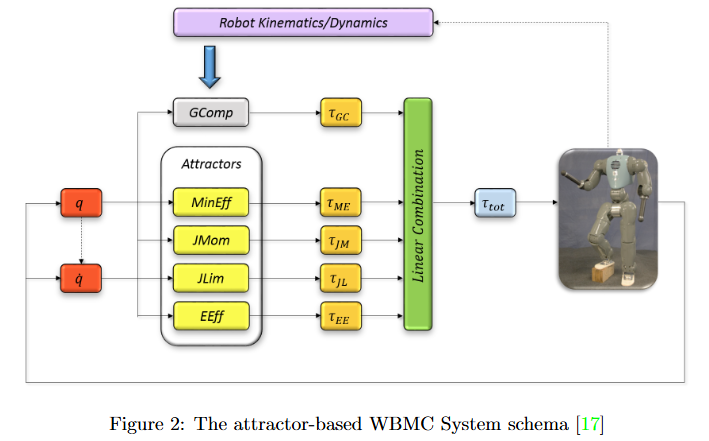
图解说明：

1. Robot Kinematics/Dynamics

这是整个控制系统的起点，表示机器人的运动学和动力学模型。
它提供了机器人当前状态的信息，包括关节位置 qq 和速度 q˙q˙，这些信息被传递到后续模块中。

2. GComp (Gravity Compensation)

重力补偿模块计算所需的力矩 τGCτGC，以抵消重力对机器人关节的影响。
这样可以确保机器人在执行其他任务时不会因为重力而产生不必要的运动或力矩。

3. Attractors

吸引子模块包含多个子模块，每个子模块代表一个特定的任务或目标：
- MinEff: 最小努力（Minimum Effort），计算使机器人运动最省力的力矩 τMEτME。
- JMom: 关节动量（Joint Momentum），计算与关节动量相关的力矩 τJMτJM。
- JLim: 关节极限（Joint Limit），计算防止关节达到极限位置的力矩 τJLτJL。
- EEff: 端效应器（End-Effector），计算使端效应器（如手或脚）达到期望位置和姿态的力矩 τEEτEE。
每个吸引子模块根据当前的关节位置 qq 和速度 q˙q˙ 计算相应的力矩贡献。

4. Linear Combination

线性组合模块将所有吸引子模块和重力补偿模块计算出的力矩进行加权求和，得到总力矩 τtotτtot。
这一步骤体现了多任务之间的协调和权衡，通过适当的权重分配，确保各个任务都能在一定程度上得到满足。

5. Output to Robot

最终计算出的总力矩 τtotτtot 被发送给机器人，驱动其关节运动，实现预期的全身运动控制效果。

各个吸引子的力矩输出实现

最小努力

关节动量

关节极限

末端执行器位置

力矩整合

关于人形机器人驱动协议

依然需要引入P，此时P的定义是：

3.3 Whole-body Multi-Objective Control 全身多目标控制

这个方法很妙！第二个任务起全部并行，内部执行权重分配，输出则通过零空间+累计投影矩阵对主任务进行避让！

1. 高优先级子任务 (High-priority subtasks)

强碰撞避免 (Strong Collision Avoidance)：确保机器人在遇到潜在的强烈碰撞时能够迅速采取措施。

1. 低优先级子任务 (Low-priority subtasks)

这些任务包括：
- 弱碰撞避免 (Weak Collision Avoidance)：处理较轻微的碰撞风险。
- 奇异性避免 (Singularity Avoidance)：防止机器人关节配置进入奇异点，奇异点是机器人运动学中的特殊位置，在这些位置上，机器人的自由度会减少，可能导致控制失效。
- 机械末端停止 (Mechanical End Stops)：确保机器人关节不会超出其物理极限。
- 躯干和基座的阻抗 (Impedance for Torso and Base)：调节机器人躯干和基座对环境作用力的响应特性。
- 零空间阻尼 (Null Space Damping)：在不干扰主要任务的情况下，抑制不必要的振动或运动。
这些子任务通过**零空间投影 (Null Space Projection)**进行整合，这意味着它们在不影响更高优先级任务的前提下被执行。

2. 定位与规划及轨迹生成 (Localization & Planning & Trajectory Generation)

这个模块负责确定机器人的当前位置、规划其未来的动作以及生成具体的运动轨迹。它为后续的控制步骤提供必要的信息和指令。

3. 笛卡尔阻抗控制 (Cartesian Impedance Control)

基于上述定位和规划的结果，此模块计算出期望的力和力矩，以便机器人能够在笛卡尔空间中按照预定的轨迹移动，同时保持适当的柔顺性以适应环境变化。

4. 关节级控制和机器人 (Joint-level control and robot)

在这一阶段，控制信号被转换为针对各个关节的具体指令。
- 扭矩控制 (Torque Control)：直接控制关节电机的输出力矩，适用于上半身（Upper Body）的精细操作。
- 速度控制 (Velocity Control)：控制关节的速度，适用于下半身（Mobile Base）的大范围移动。
允许控制 (Admittance Control)：根据外部力反馈调整机器人的运动，增强其与环境的交互能力。

3.4 不同控制器生成行为的示例

本节详细比较了三种不同类型的全身控制（WBC）方案所产生的行为：分层WBC、加权WBC和混合分层/加权WBC。比较是通过一个简单的平面冗余机械系统进行的，该系统有两个分支，如图4所示。

该图展示了同一机械系统在三种不同控制器下的行为：

第一行：分层WBC
第二行：加权WBC
第三行：混合WBC

每一列代表任务的顺序激活：

地面上COM投影位置的任务。
右侧分支末端执行器位置的任务。
左侧分支末端执行器位置的任务。

任务及其优先级

第一任务：地面上COM投影的位置。
第二任务：右侧分支末端执行器的位置。
第三任务：左侧分支末端执行器的位置。

在分层WBC中，这些任务具有严格的优先级顺序。在加权WBC中，每个任务都有一个相关的权重并独立作用。在混合WBC中，第一个任务比其他两个任务具有更高的优先级，但第二个和第三个任务之间的相对重要性由它们的权重决定。

情况1：分层WBC

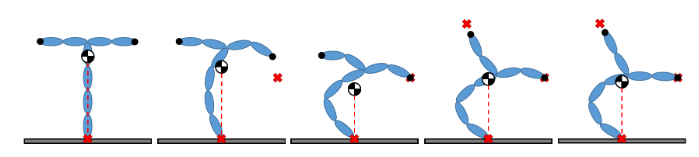
初始状态：在时间零点，仅控制COM投影的位置。系统以零速度从'T'配置开始，并保持其位置不变。
任务激活：当第二个任务（右端执行器位置）被激活时，系统开始移动以满足这一新需求，同时保持COM投影的位置不变。
行为：过渡阶段和稳态都显示COM投影未受干扰。两个任务的误差都减小到零。然而，当第三个任务（左端执行器位置）被激活时，由于前两个任务施加的约束，它无法完全完成。第三个任务位置的误差被最小化但未达到零。

情况2：加权WBC

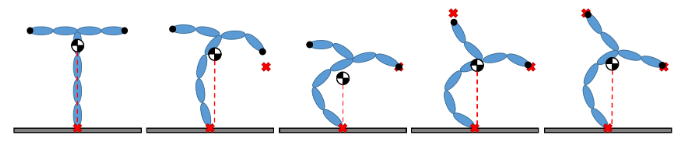
任务激活：当第二个任务（右端执行器位置）被激活时，系统配置开始变化。第一个任务受到影响，在过渡阶段，COM投影略微偏离参考位置。
稳态：在稳态下，机器人的冗余性使其能够完美满足两个任务，结果误差为零。然而，激活第三个任务（左端执行器位置）会扰动前两个任务。达成一种妥协，其中没有任务达到零误差条件，误差在任务之间分配。调整权重可以使某些任务优于其他任务。

情况3：混合分层/加权WBC

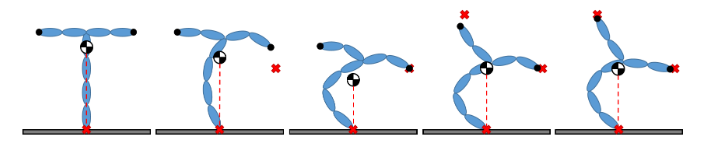
任务激活：当第二个任务（右端执行器位置）被激活时，系统开始移动以满足这一新需求，同时保持质心（COM）投影的位置不变。
行为：过渡阶段和稳态都显示质心（COM）投影保持不变。两个任务的误差都被最小化到零。然而，当第三个任务（左端执行器位置）被激活时，它可以在不影响前两个任务的情况下进行调整，因为它的权重较低，且前两个任务具有更高的优先级。最终，系统能够在保持高优先级任务的同时，尽可能地完成低优先级任务。

查看全文

http://www.dtcms.com/a/593043.html