当前位置：首页 > news >正文

LeetCode hot100:240 搜索二维矩阵 II：三种解法对比

news 2025/11/11 8:28:41

问题描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
每列的元素从上到下升序排列。

示例1

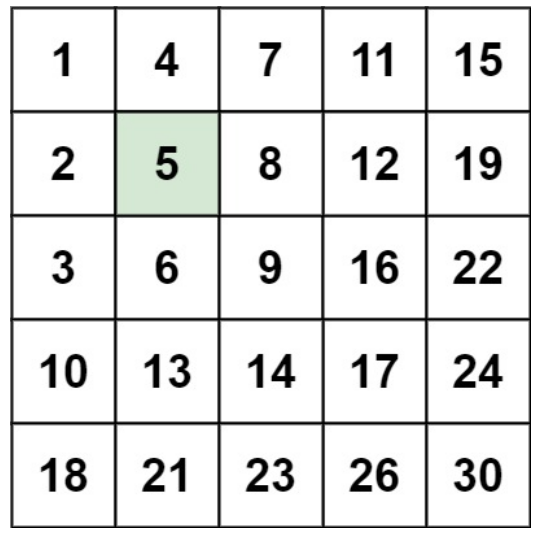
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]]

target = 5

输出：true

示例2：

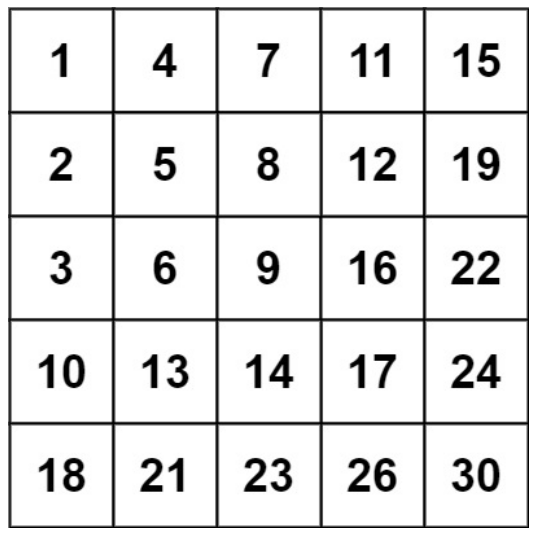
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]]

target = 20

输出：false

解决方法：

方法一：直接查找（暴力解法）

算法思路：

遍历矩阵中的每一个元素
如果找到目标值，立即返回 true
如果遍历完所有元素都没有找到，返回 false

代码实现：

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:if not matrix or not matrix[0]:return False# 直接查找for row in matrix:for element in row:if element == target:return Truereturn False

复杂度分析：

时间复杂度:O(m × n) 需要遍历矩阵中的所有元素，在最坏情况下需要检查 m × n 次
空间复杂度:O(1) 只使用了常数级别的额外空间

优缺点：

优点：实现简单，代码直观易懂
缺点：没有利用矩阵的有序特性，效率较低

方法二：从右上角开始搜索（Z字形查找）

算法思路：

从矩阵的右上角 (0, n-1) 开始搜索
比较当前元素与目标值：
- 如果相等，返回 true
- 如果当前元素大于目标值，说明目标值不可能在当前列，向左移动一列
- 如果当前元素小于目标值，说明目标值不可能在当前行，向下移动一行
如果搜索超出矩阵边界，返回 false

代码实现：

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:if not matrix or not matrix[0]:return False# 右上角开始m , n = len(matrix) , len(matrix[0])row,col = 0,n-1while row < m and col >= 0:if matrix[row][col] == target:return Trueelif matrix[row][col] > target:col -= 1else:row += 1return False

复杂度分析：

时间复杂度:O(m + n) 总搜索次数为 m+n
空间复杂度:O(1) 只使用了常数级别的额外空间

方法三：从左下角开始搜索（Z字形查找）

算法思路：

从矩阵的左下角 (m-1, 0) 开始搜索
比较当前元素与目标值：
- 如果相等，返回 true
- 如果当前元素大于目标值，说明目标值不可能在当前行，向上移动一行
- 如果当前元素小于目标值，说明目标值不可能在当前列，向右移动一列
如果搜索超出矩阵边界，返回 false

代码实现：

class Solution:def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:if not matrix or not matrix[0]:return False# 左下角开始row_len = len(matrix)list_len = len(matrix[0])first = row_len - 1second = 0while first >= 0 and second < list_len:flag = matrix[first][second]if flag == target:return Trueelif flag < target:second += 1else:first -= 1return False

复杂度分析：