数据结构(18)
目录
一、关键路径
1、关键路径的核心定义与本质
(1)定义
(2)本质
2、关键路径的核心关联概念(时间参数)
(1)事件的时间参数(顶点层面)
(2)活动的时间参数(边层面)
(3)关键活动的判定
3、关键路径的判定步骤(示例演示)
4、关键路径的核心特性
5、关键路径的应用价值
6、关键路径与最短路径的区别
一、关键路径
关键路径(Critical Path)是AOE 网(边表示活动的带权有向无环图) 中的核心概念,指从源点(项目开始事件)到汇点(项目结束事件)的最长路径。它决定了项目的最短完成时间,路径上的所有活动(边)均为 “关键活动”—— 任何关键活动的延误都会直接导致项目总工期延长,而非关键活动则有一定时间缓冲。
1、关键路径的核心定义与本质
(1)定义
在 AOE 网中,关键路径是满足以下条件的路径:
- 路径起点为源点(入度为 0,项目开始事件),终点为汇点(出度为 0,项目结束事件)。
- 路径上所有活动的权值(持续时间)之和最大 —— 这个总和就是项目的最短完成时间(无法再缩短,因所有关键活动已无缓冲)。
(2)本质
关键路径的核心是 “项目的最长依赖链”:
- 项目中存在多个并行活动流程,但必须等所有流程中 “最慢的那条” 完成,项目才能整体结束。
- 这条 “最慢的流程” 就是关键路径,它的总时长直接决定了项目的最短工期。
2、关键路径的核心关联概念(时间参数)
关键路径的判定依赖 AOE 网的 4 个核心时间参数(需先计算这些参数才能确定关键路径):
(1)事件的时间参数(顶点层面)
- 事件最早发生时间(ve(i)):顶点i(事件)最早能发生的时间,即所有到达该顶点的活动都完成的最早时刻。
- 源点源点(项目从时间 0 开始)。
- 其他顶点:权重(取所有前置活动完成时间的最大值,需等最后一个前置活动结束)。
- 事件最迟发生时间(vl(i)):顶点i(事件)最迟必须发生的时间,超过则延误项目总工期。
- 汇点汇点汇点(汇点的最早、最迟时间一致,即项目最短完成时间)。
- 其他顶点:权重(取所有后续活动最迟开始时间的最小值,不延误后续流程)。
(2)活动的时间参数(边层面)
- 活动最早开始时间(e(k)):边<i,j>(活动k)最早能开始的时间,即起点事件i的最早发生时间:e(k)=ve(i)。
- 活动最迟开始时间(l(k)):边<i,j>(活动k)最迟必须开始的时间,即终点事件j的最迟发生时间减去活动持续时间:权重。
(3)关键活动的判定
- 活动的时间余量:l(k)−e(k)(活动可延误的最大时间,不影响项目总工期)。
- 关键活动:l(k)−e(k)=0(无时间余量,必须按时开始、完成,否则延误项目)。
- 关键路径:由所有关键活动串联而成的路径(从源点到汇点)。
3、关键路径的判定步骤(示例演示)
以 “软件项目开发 AOE 网” 为例,演示关键路径的判定过程:
(1)AOE 网基础结构
- 顶点(事件):V0(项目开始)、V1(需求分析完成)、V2(设计完成)、V3(开发完成)、V4(测试完成)、V5(项目结束)。
- 边(活动 + 持续时间):<V0,V1>(5)、<V1,V2>(3)、<V2,V3>(8)、<V3,V4>(2)、<V4,V5>(4)、<V2,V4>(3)。
(2)步骤 1:计算事件的最早发生时间(ve)
- ve(0)=0(源点)
- ve(1)=ve(0)+5=5
- ve(2)=ve(1)+3=8
- ve(3)=ve(2)+8=16
- ve(4)=max{ve(3)+2,ve(2)+3}=max{18,11}=18
- ve(5)=ve(4)+4=22(项目最短完成时间 = 22)
(3)步骤 2:计算事件的最迟发生时间(vl)
- vl(5)=ve(5)=22(汇点)
- vl(4)=vl(5)−4=18
- vl(3)=vl(4)−2=16
- vl(2)=min{vl(3)−8,vl(4)−3}=min{8,15}=8
- vl(1)=vl(2)−3=5
- vl(0)=vl(1)−5=0
(4)步骤 3:计算活动的时间参数与关键活动
| 活动(边) | e(k)=ve(i) | 权重 | 时间余量l−e | 是否关键活动 |
|---|---|---|---|---|
| <V0,V1> | 0 | 5−5=0 | 0 | 是 |
| <V1,V2> | 5 | 8−3=5 | 0 | 是 |
| <V2,V3> | 8 | 16−8=8 | 0 | 是 |
| <V3,V4> | 16 | 18−2=16 | 0 | 是 |
| <V4,V5> | 18 | 22−4=18 | 0 | 是 |
| <V2,V4> | 8 | 18−3=15 | 7 | 否 |
(5)步骤 4:确定关键路径
关键活动串联的路径:V0→V1→V2→V3→V4→V5,总长度 = 5+3+8+2+4=22(与项目最短完成时间一致)。
例题:
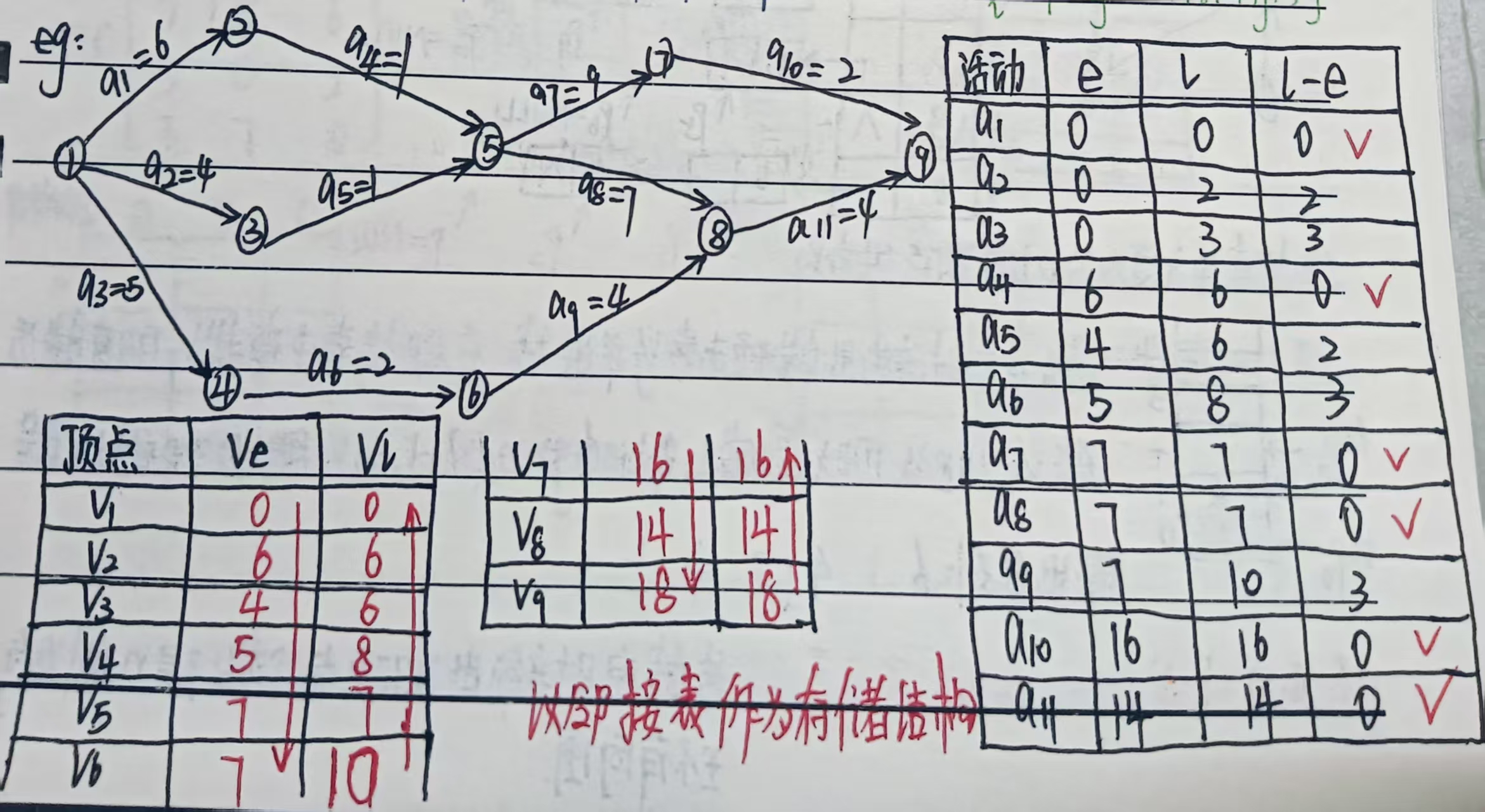

4、关键路径的核心特性
- 总时长 = 项目最短完成时间:关键路径的权值和是所有路径中最大的,必须等这条路径上的所有活动完成,项目才能结束。
- 关键活动无缓冲:路径上的每个活动都没有时间余量,任何一个关键活动延误t天,项目总工期就延误t天。
- 非关键活动有缓冲:非关键活动的时间余量内延误,不影响项目总工期(如示例中<V2,V4>可延误 7 天)。
- 关键路径可能不唯一:若 AOE 网中存在多条 “权值和最大” 的路径,则这些路径都是关键路径,项目总工期由所有关键路径的共同时长决定(需确保所有关键路径都按时完成)。
5、关键路径的应用价值
关键路径是项目管理和流程优化的核心工具,核心价值体现在:
- 确定项目最短工期:直接给出项目的最小完成时间,为项目计划制定提供依据。
- 聚焦核心任务:明确关键活动,便于资源倾斜(如人力、物力优先投入关键活动,确保不延误)。
- 优化项目流程:
- 缩短项目工期:只能通过压缩关键活动的持续时间(如优化流程、增加资源),压缩非关键活动无意义。
- 平衡资源:在不延误总工期的前提下,可将非关键活动的资源调配到关键活动,提升整体效率。
- 风险预警:实时监控关键活动的进度,提前发现延误风险,及时调整计划。
6、关键路径与最短路径的区别
| 对比维度 | 关键路径(AOE 网) | 最短路径(带权图) |
|---|---|---|
| 路径性质 | 源点到汇点的最长路径 | 源点到目标点的最短路径 |
| 应用场景 | 项目工期规划、流程优化 | 路径规划(距离、时间、成本最小) |
| 核心目标 | 确定项目最短完成时间,识别关键活动 | 寻找权值和最小的路径 |
| 依赖模型 | 带权有向无环图(AOE 网) | 带权图(有向 / 无向,可含负权) |
关键路径的核心是 AOE 网中 “最长的活动依赖链”,它决定了项目的最短完成时间,路径上的关键活动是项目管理的核心重点。通过计算事件和活动的时间参数,可精准识别关键路径和关键活动,为项目工期规划、资源调配和风险控制提供科学依据,是工程管理、生产调度、项目开发等场景的核心优化工具。
